-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2016; 6(4): 117-122
doi:10.5923/j.ijtmp.20160604.02

Nonlinear Interaction of Underdense Plasma by a High-intensity Pulse
Fereydoon Ataei1, Davoud Dorranian2, Negar Motakef-Kazemi3
1Department of Computer, Shahryar Branch, Islamic Azad University, Tehran, Iran
2Plasma Physics Research Center, Science and Research Branch, Islamic Azad University, Tehran, Iran
3Department of Nanochemistry, Faculty of Pharmaceutical Chemistry, Pharmaceutical Sciences Branch, Islamic Azad University, Tehran, Iran (IAUPS)
Correspondence to: Fereydoon Ataei, Department of Computer, Shahryar Branch, Islamic Azad University, Tehran, Iran.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

This research is theoretically studied the nonlinear interaction of high-intensity laser pulse by underdense plasma. Also ohm heat and driving force effects of ponderomotive energy is considered. The driving force can be obtained by electron density, temperature and dielectric magnetic influence distribution in a nonrelativistic system through indirectly plasma. The ponderomotive energy is nonlinearly and the ponderomotive force of laser pulse is included compressed plasma electrons from the regions of high-intensity laser. The plasma length parameter and fixed solution in Maxwell and hydrodynamic equations can be obtained by the electron density, temperature distribution, effective magnetic influence change, electric and magnetic field. Also the fourth method of the Runge-Kutta programming language is used in this study. It has been shown that intensity increase of laser pulse is caused decrease of electron density and increase of dielectric constant. Since electron decrease, electric and magnetic field oscillation wavelength are resulted increase of dielectric constant. Increasing of laser pulse intensity, electric and magnetic field are nonsinusoidal and nonlinear in plasma. The oscillation of the electron density is sharply peaked. Also the effect of laser intensity increase is caused the spread increase and wavelength decrease in fluctuation of electron.
Keywords: Nonlinear interaction, Underdense plasma, Laser pulse
Cite this paper: Fereydoon Ataei, Davoud Dorranian, Negar Motakef-Kazemi, Nonlinear Interaction of Underdense Plasma by a High-intensity Pulse, International Journal of Theoretical and Mathematical Physics, Vol. 6 No. 4, 2016, pp. 117-122. doi: 10.5923/j.ijtmp.20160604.02.
1. Background
- Many important researches have studied the propagation of high-intensity laser plasma [1-2]. The researchers were investigated the optimization of plasma effect in laser and effect of plasma density and laser energy on the stability of produced laser electron beams [3-4]. Recently, the interaction of the underdense plasma beam has been developed as the most advanced area of study [5-6]. In the last decade, the nonlinear interaction of high-intensity laser beam was regarded as an extremely interesting science [7]. Many nonlinear physical processes can affect the propagation of intense pulse [8-9]. The formula of nonlinear theory was studied for beam interaction with plasma. Also the effect of generated hydrodynamic instability was investigated in underdense beam under certain conditions [10]. Recently, the scientists were investigated the effect of external magnetic field on density distribution, electromagnetic field and plasma [11-12]. Also the dependence of electron is investigated by an electromagnetic wave of plasma and the influence of the initial parameters of the magnetic field [13-14]. The ponderomotive force is a nonlinear force in an inhomogeneous oscillating electromagnetic field that emitted electron from plasma [15-16]. This force is the nonlinear interaction of high-intensity laser pulse with the collisional homogenous underdense plasma that depended on the laser pulse [17-18]. The effect of ponderomotive force was freely studied on the interaction of high-intensity laser pulse in underdense plasma by expanding of plasma regime [19-20]. The acceleration of electron is the major application of laser acceleration in high-intensity laser beam [21-22]. The electron beam was generated by the electron accelerator and the huge field of the intense laser pulse [23-24]. The electromagnetic field can exert a force on the charged particles through the mean square of electric field [25-26]. The collision of nonlinear electromagnetic plasma was generated the ponderomotive force that created the nonlinearity ohm in the plasma [27]. The effect of pulse duration was experimentally presented self-focusing laser by dense plasma [28]. The Maxwell and nonlinear differential equations were investigated by the electron density distribution and field profile in underdense magnetized plasma using the direct one-dimensional (1D) motion of the electric field that used to calculate the hydrodynamic equations [29]. In this study, the nonlinear interaction of intense laser pulse is studied with the one-dimensional motion of underdense plasma in a magnetic field using the Maxwell and hydrodynamic equations. The changes are investigated wavelength, intensity of laser, density and temperature electron, electric and magnetic field.
2. Theory
- The interaction of laser with plasma has the important application in various fields such as laser particle accelerator and production of gamma ray. The interaction is followed by
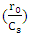 function where
function where 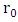 and
and 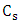 are the size of laser and speed of sound respectively if
are the size of laser and speed of sound respectively if 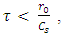 and
and 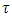 is the length of laser pulse. In this case, the radiation effect of laser pulse can be ignored on the ions in the plasma as the ions are considered resident. While if
is the length of laser pulse. In this case, the radiation effect of laser pulse can be ignored on the ions in the plasma as the ions are considered resident. While if 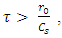 the ions can be fluctuated with ion plasma frequency
the ions can be fluctuated with ion plasma frequency 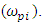 This research has been showed the interaction of high-intensity laser pulse with underdense plasma of magnetic collision in the presence of external charge. In the case
This research has been showed the interaction of high-intensity laser pulse with underdense plasma of magnetic collision in the presence of external charge. In the case 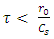 is used, and the effect of laser pulse radiation is ignored on ions in plasma. If the intensity of electromagnetic wave was carried the lower energy for the relativistic self–focusing that considered:
is used, and the effect of laser pulse radiation is ignored on ions in plasma. If the intensity of electromagnetic wave was carried the lower energy for the relativistic self–focusing that considered: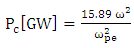 | (1) |
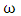 and
and 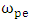 are electromagnetic wave frequency and electron plasma frequency respectively. The critical density, electron density, and flow intensity are considered
are electromagnetic wave frequency and electron plasma frequency respectively. The critical density, electron density, and flow intensity are considered 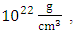
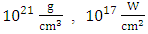 respectively. Based on
respectively. Based on 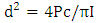 where d is the diameter of focal point and lower than 6 micrometer since the laser wavelength could be applied within 8 µm. The radiation effects are ignored according to the initial assumptions. The laser intensity is increased according to the formula
where d is the diameter of focal point and lower than 6 micrometer since the laser wavelength could be applied within 8 µm. The radiation effects are ignored according to the initial assumptions. The laser intensity is increased according to the formula 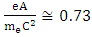 where (e) the electron charge, (A) the number vector potential, (me) the electron mass and (c) the light speed. The range of natural vector potential can have ignored from
where (e) the electron charge, (A) the number vector potential, (me) the electron mass and (c) the light speed. The range of natural vector potential can have ignored from 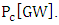 Based on the hypothesis, the electron density is higher than critical density therefore laser pulse duration is longer than plasma thickness and electron density is lower than original density. The length of space pulse would be longer than 30 µm that involved plasma density and standing wave, which could be considered through a generated pulse. So the Maxwell's and hydrodynamic equations can be calculated electric and magnetic field, temperature and density distribution for electron in the presence of a magnetic field. The fluctuation wavelength of magnetic and electric field was decreased by the increasing of laser intensity. At the same time, the dielectric constant is increased that caused the significant increase of electron density. Thus the effective magnetic diffusion and electron temperature fluctuation are increased. Also the wavelength of fluctuation, electron temperature and effective magnetic influence fluctuation are reduced. The temperature distribution could be obtained by
Based on the hypothesis, the electron density is higher than critical density therefore laser pulse duration is longer than plasma thickness and electron density is lower than original density. The length of space pulse would be longer than 30 µm that involved plasma density and standing wave, which could be considered through a generated pulse. So the Maxwell's and hydrodynamic equations can be calculated electric and magnetic field, temperature and density distribution for electron in the presence of a magnetic field. The fluctuation wavelength of magnetic and electric field was decreased by the increasing of laser intensity. At the same time, the dielectric constant is increased that caused the significant increase of electron density. Thus the effective magnetic diffusion and electron temperature fluctuation are increased. Also the wavelength of fluctuation, electron temperature and effective magnetic influence fluctuation are reduced. The temperature distribution could be obtained by 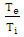 in plasma where Ti and Te are ion temperature and electron temperature respectively. The nonlinear propagation is considered for high-intensity laser pulse with collision of underdense plasma in a magnetic field for the area Z> 0. The laser pulse was spread during Z in plasma thus based on the assumptions in above the ion is immovability in plasma because it is heavily. The Maxwell's and hydrodynamic equations will have:
in plasma where Ti and Te are ion temperature and electron temperature respectively. The nonlinear propagation is considered for high-intensity laser pulse with collision of underdense plasma in a magnetic field for the area Z> 0. The laser pulse was spread during Z in plasma thus based on the assumptions in above the ion is immovability in plasma because it is heavily. The Maxwell's and hydrodynamic equations will have: 
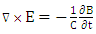 | (2) |
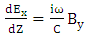 | (3) |
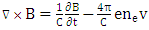 | (4) |
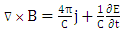 | (5) |
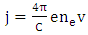 | (6) |
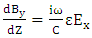 | (7) |
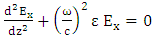 | (8) |
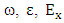 and
and 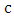 are laser frequency, dielectric constant coefficient, electric field of plasma, speed of light respectively. To solve of equation 8, dielectric constant of the plasma is equal:
are laser frequency, dielectric constant coefficient, electric field of plasma, speed of light respectively. To solve of equation 8, dielectric constant of the plasma is equal: 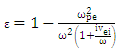 | (9) |
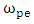 is
is 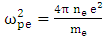 that is plasma electron frequency. The
that is plasma electron frequency. The 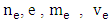 and
and 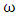 are electron density, electron charge, electron mass, electron collision frequency, electromagnetic wave frequency respectively. The plasma electric constant is used to solve equation through MATLAB programming language and fourth method of Runge-Kutta as follows: 1=0.58del =le-3;kesi =1;function dy = nonlinear(t, y)dy =zeros(2,1)l =0.58;del =le-3;kesi =1;dy(1)=y(2);dy(2)=(1.*exp(-y (1).^2/3*del.*kesi)+0.004* y(1) /kesi.*(1+(y(1).^2)/3*del.*kesi))-1).*y(1);[t,y]=ode 45 (@nonlinear, [0 30], [0 0.8]);Figure ('name ', E field);Plot (t, y (:1);The
are electron density, electron charge, electron mass, electron collision frequency, electromagnetic wave frequency respectively. The plasma electric constant is used to solve equation through MATLAB programming language and fourth method of Runge-Kutta as follows: 1=0.58del =le-3;kesi =1;function dy = nonlinear(t, y)dy =zeros(2,1)l =0.58;del =le-3;kesi =1;dy(1)=y(2);dy(2)=(1.*exp(-y (1).^2/3*del.*kesi)+0.004* y(1) /kesi.*(1+(y(1).^2)/3*del.*kesi))-1).*y(1);[t,y]=ode 45 (@nonlinear, [0 30], [0 0.8]);Figure ('name ', E field);Plot (t, y (:1);The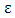 is represented dielectric constant. In electromagnetic waves, the propagation of laser pulse is same something that makes the difference in propagation circumstances and
is represented dielectric constant. In electromagnetic waves, the propagation of laser pulse is same something that makes the difference in propagation circumstances and 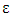 plays a very important role in propagation. The dielectric constant in plasma interaction is as follows:
plays a very important role in propagation. The dielectric constant in plasma interaction is as follows: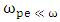 | (10) |
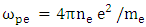 where e, ne and me are electron charge, electron charge density and electron mass respectively. The plasma does not adapt to the temperature of interaction thus the electron temperature can be changed. The change of electron temperature will be resulted to collisions during the interaction. The electron oscillation velocity and electron vibrational motion are obtained in laser pulse through equation as follows:
where e, ne and me are electron charge, electron charge density and electron mass respectively. The plasma does not adapt to the temperature of interaction thus the electron temperature can be changed. The change of electron temperature will be resulted to collisions during the interaction. The electron oscillation velocity and electron vibrational motion are obtained in laser pulse through equation as follows: 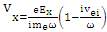 | (11) |
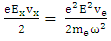 | (12) |
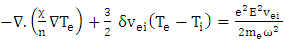 | (13) |
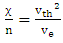 and
and 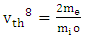 where vth is the velocity of electron temperature. If the free mean time of electron is small, the first letter of left side is ignored and the electron temperature is finally obtained as follows:
where vth is the velocity of electron temperature. If the free mean time of electron is small, the first letter of left side is ignored and the electron temperature is finally obtained as follows: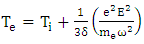 | (14) |
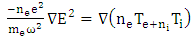 | (15) |
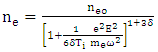 | (16) |
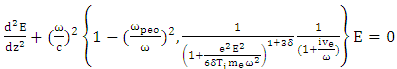 | (17) |
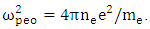 The term of plasma length is obtained through a longitudinal section of electromagnetic field, electron density, temperature distribution and effective magnetic permeability. The equation is resolved as follows:
The term of plasma length is obtained through a longitudinal section of electromagnetic field, electron density, temperature distribution and effective magnetic permeability. The equation is resolved as follows: 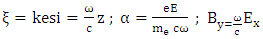 | (18) |
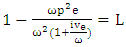 | (19) |
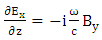 | (20) |
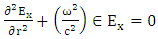 | (21) |
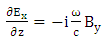 | (22) |
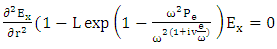 | (23) |
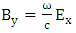 | (24) |
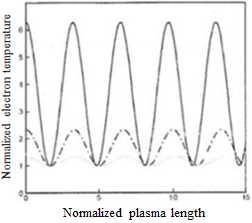
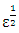 . The longitudinal section of field is nonlinear and nonsinusoidal through the current increase in laser energy. Figure 1 and 2 are shown the effect of laser intensity on electric field (E) and magnetic field (B) as a function of plasma length (Z). Figure 3 and 4 are shown the effect of laser intensity on electron density
. The longitudinal section of field is nonlinear and nonsinusoidal through the current increase in laser energy. Figure 1 and 2 are shown the effect of laser intensity on electric field (E) and magnetic field (B) as a function of plasma length (Z). Figure 3 and 4 are shown the effect of laser intensity on electron density 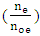 and electron temperature
and electron temperature 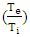 as a function of plasma length. At the same time, the increase of laser intensity is caused the decrease of wavelength. The high-intensity laser is observed that the start point of sinusoidal shape change in electron density
as a function of plasma length. At the same time, the increase of laser intensity is caused the decrease of wavelength. The high-intensity laser is observed that the start point of sinusoidal shape change in electron density 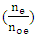 is stronger than the start point of field. Also, the start point of sinusoidal shape is observed the equal for the distribution of normalized electron temperature. Figure 5 is shown the effect of laser intensity on effective permeability
is stronger than the start point of field. Also, the start point of sinusoidal shape is observed the equal for the distribution of normalized electron temperature. Figure 5 is shown the effect of laser intensity on effective permeability 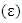 as a function of plasma length. The increase of laser intensity is resulted to the electron temperature and the increase of magnetic permeability that the electron temperature is more than the ion temperature at this time and the wavelength is decreased for these oscillations. Furthermore, the increase of laser intensity can be deviated the effective magnetic oscillation from the sinusoidal shape [30]. There is
as a function of plasma length. The increase of laser intensity is resulted to the electron temperature and the increase of magnetic permeability that the electron temperature is more than the ion temperature at this time and the wavelength is decreased for these oscillations. Furthermore, the increase of laser intensity can be deviated the effective magnetic oscillation from the sinusoidal shape [30]. There is 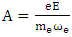 as the normalized electric field where
as the normalized electric field where 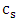 is sound velocity,
is sound velocity, 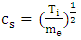 and
and 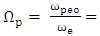
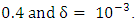 In all figures, the normalized frequency
In all figures, the normalized frequency 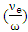 is fixed by which
is fixed by which 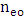 is close to the main density, moreover the wavelength of normalized plasma is made as the
is close to the main density, moreover the wavelength of normalized plasma is made as the 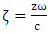 function.
function.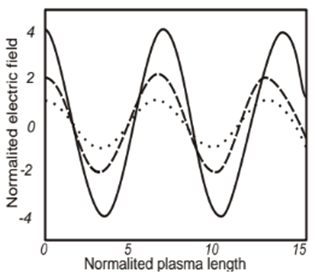 | Figure 1. Changes in normalized electric field (E) as a function of plasma length (Z) for the various laser intensities 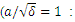 dotted line dotted line 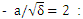 bold dotted line - bold dotted line - 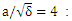 line) line) |
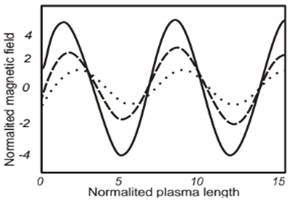 | Figure 2. Changes in normalized magnetic field (B) as a function of plasma length (Z) for the various laser intensities 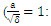 dotted line - dotted line - 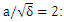 bold dotted line - bold dotted line - 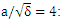 line) line) |
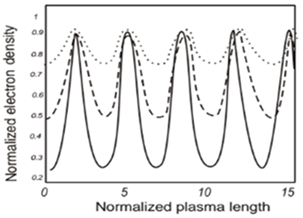 | Figure 3. Changes in normalized electron density 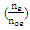 as a function of plasma length (Z) for the various laser intensities as a function of plasma length (Z) for the various laser intensities 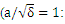 dotted line - dotted line - 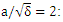 bold dotted line - bold dotted line - 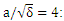 line) line) |
 | Figure 4. Changes in normalized electron temperature 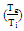 as a function of plasma length (Z) for the various laser intensities as a function of plasma length (Z) for the various laser intensities 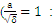 dotted line - dotted line - 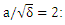 bold dotted line - bold dotted line - 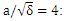 line) line) |
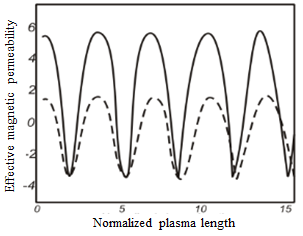 | Figure 5. Changes in effective magnetic permeability 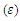 as a function of plasma length (Z) for the various laser intensities as a function of plasma length (Z) for the various laser intensities 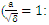 dotted line - dotted line - 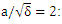 bold dotted line - bold dotted line - 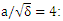 line) line) |
3. Results and Discussion
- According to above equations, the interaction of high-intensity laser pulse is strongly nonlinear equation with underdense magnetic plasma and there is no analytical solution. Since the equations are solved by the fourth method of Runge-Kutta and MATLAB programming language. The increase of laser intensity is caused the increase of oscillation expansion when the energy flow is amplitude square. Also the oscillation wavelength of plasma is reduced in magnetic and electric field because laser intensity is increased and electron density is reduced. At the result, the dielectric constant is increased since the electric oscillation wavelength is reduced. The longitudinal section of field is nonlinear and nonsinusoidal because the increase of energy. The increase of laser intensity is caused that the electron density and temperature distribution are shown as the plasma length function along the z axis in the images. Also density and temperature oscillation are strongly peaked for electron. At this time, the wavelength is reduced because the plasma is in magnetic environment. Also the increase of laser intensity is caused that the electron temperature is 8 times greater than the ion temperature. The oscillation of effective magnetic permeability is significantly increased and the wavelength is reduced. In the normalized electric field, there is
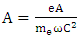 when
when 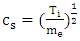 as the sound speed,
as the sound speed, 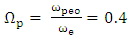 as natural collision frequency in plasma, and
as natural collision frequency in plasma, and 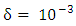 that there is
that there is 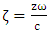 due to
due to 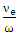 is given.
is given. 4. Conclusions
- In this study, the intense of laser interaction with magnetic plasma is investigated by Maxwell and hydrodynamic equations, the ponderomotive force, electron ohm heat, the longitudinal section in the electric and magnetic field of laser pulse, the oscillation in plasma, electron density and temperature distribution inside the plasma. The oscillation wavelength of the longitudinal section is decreased in the field and the oscillation expansion is increased. The increase of laser intensity is strongly peaked the effective magnetic permeability, temperature and electron density oscillation because of the nonlinear ohm effect and the wavelength is simultaneously decreased. The laser intensity is increased due to the pulse length of laser is increaser than the plasma thickness and the magnetic environment. In length section of electric and magnetic field, the oscillation wavelength is reduced but oscillation expansion is increased. The increase of laser intensity is dramatically increased density, temperature and effective magnetic permeability for electron in plasma since the reduce of them is because of the ohm effect of the magnetic field.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML