N. Yakubu1, S. X. K. Howusu2, W. L. Lumbi3, N. Ibrahim4
1Department of Physics, University of Maiduguri, Maiduguri, Nigeria
2National Mathematics Centre Abuja, Abuja, Nigeria
3Department of Physics, Nasarawa State University Keffi, Keffi, Nigeria
4M.Sc Student Department of Physics, University of Jos, Jos, Nigeria
Correspondence to: N. Ibrahim, M.Sc Student Department of Physics, University of Jos, Jos, Nigeria.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
AbstractIt is well known that Newton’s dynamical gravitational field equation and Einstein’s geometrical gravitational field equation were derived based upon the Euclidean geometry. In this paper, we used a golden metric tensor for all gravitational fields in nature to develop Riemannian Laplacian field equation which is assumed to be more general than the Euclidean geometry in order to derive Riemann’s dynamical gravitational field equation for a static homogeneous oblate spheroidal massive bodies due correction terms of all order c-2 that is not found in Newton’s gravitational field equation and also in this paper we derived the solution of Newton’s gravitational field equation for a static homogeneous oblate spheroidal massive body.
Keywords:
Golden metric tensor, Riemannian Laplacian Equation, Spherical polar coordinates, Oblate spheroidal coordinates
Cite this paper: N. Yakubu, S. X. K. Howusu, W. L. Lumbi, N. Ibrahim, Solution of Newton’s Gravitational Field Equation of a Static Homogeneous Oblate Spheroidal Massive Body, International Journal of Theoretical and Mathematical Physics, Vol. 6 No. 3, 2016, pp. 104-109. doi: 10.5923/j.ijtmp.20160603.03.
1. Introduction
In the last six decades, the theoretical study of gravitational fields in Newton’s dynamical gravitational field equation was treated under the assumption that massive bodies are perfectly spherical in nature. In the same way, Einstein’s Geometrical gravitational field equation was treated under the assumption that the sun is exclusively a perfect sphere as seen in Schwarzschild’s solution to Einstein’s Geometrical gravitational field equation. It is well known that Newton’s dynamical gravitational field equation and Einstein’s geometrical gravitational field equation were derived based upon the Euclidean Laplacian operator. Recently, research has shown that all rotating bodies example the planets, sun, stars and the galaxies in the universe are either oblate spheroidal or prolate in shape [1, 2, 9, 10, 13].In Newton's mechanics, the motion of particles (such as projectile, satellites and pendulli) in earth's atmosphere is treated under the assumption that the earth is a perfect sphere [14]. Similarly, in the solar system the motion of bodies (such as planets comets and asteroids) is treated under the assumption that the Sun is a perfect sphere [3, 12].Also in Einstein's theory, the motion of bodies (such as planets) and particles (such as photons) are treated under the assumption that the Sun is a perfect sphere (Schwarzschild spacetime). But it is well known that the only reason for these restrictions is mathematical convenience and simplicity. The real fact of nature is that all rotating planets stars and galaxies in the universe are spheroidal [5, 6, 11]. And it is obvious that their spheroidal geometry will have corresponding consequences and effects in the motion of all particles in their gravitational fields. These effects will exist in both Newtonian mechanics and in Einstein's theory.
2. Theoretical Analysis
Consider a static homogeneous oblate spheroidal massive body of rest mass M and radius 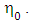 The Riemannian dynamical gravitational field equation is given explicitly by [7, 8, 10]
The Riemannian dynamical gravitational field equation is given explicitly by [7, 8, 10]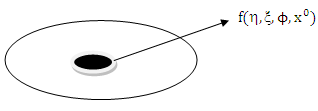 | Figure 1 |
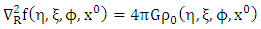 | (1.0) |
Where 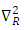 is Riemannian LaplacianGiven
is Riemannian LaplacianGiven  | (1.1) |
and 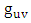 is the metric tensor (either schwarztchild or great metric tensor or golden metric tensor). Here we use golden metric tensor of oblate spheroidal coordinates. In spherical polar coordinates, Golden metric tensor is given by:
is the metric tensor (either schwarztchild or great metric tensor or golden metric tensor). Here we use golden metric tensor of oblate spheroidal coordinates. In spherical polar coordinates, Golden metric tensor is given by: 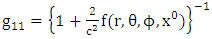 | (1.2) |
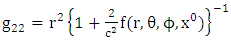 | (1.3) |
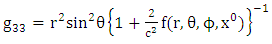 | (1.4) |
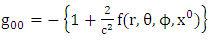 | (1.5) |
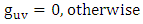 | (1.6) |
To express Golden metric tensor in oblate spheroidal coordinates, we need to transform as we shall see later. 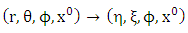 Note that:
Note that: 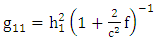 | (1.7) |
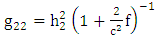 | (1.8) |
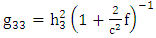 | (1.9) |
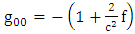 | (1.10) |
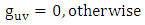 | (1.11) |
Where 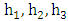 are the scale factors in oblate spheroidal coordinates to be evaluated. Now consider Riemannian Laplacian
are the scale factors in oblate spheroidal coordinates to be evaluated. Now consider Riemannian Laplacian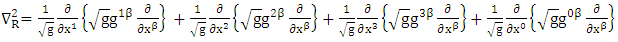 | (1.12) |
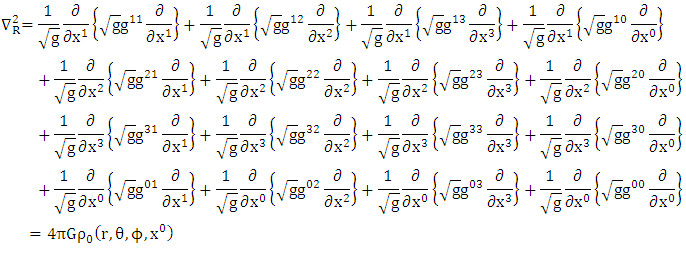 | (1.13) |
The above Riemannian field equation reduced to: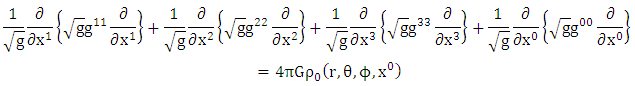 | (1.14) |
By definition 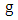 is the determinant of the Golden metric tensor
is the determinant of the Golden metric tensor 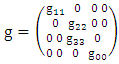 | (1.15) |
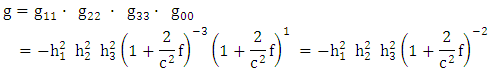 | (1.16) |
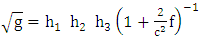 | (1.17) |
For oblate spheroidal coordinate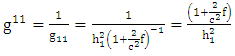 | (1.18) |
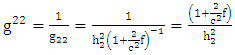 | (1.19) |
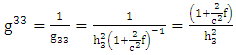 | (1.20) |
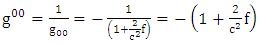 | (1.21) |
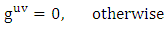 | (1.22) |
Note also the scale factors for oblate spheroidal coordinates are: 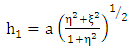 | (1.23) |
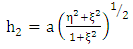 | (1.24) |
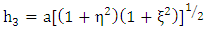 | (1.25) |
By making use of equation (1.17) above and substituting  We get:
We get: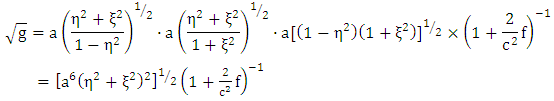 | (1.26) |
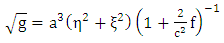 | (1.27) |
Putting 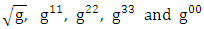 into the field equation we get
into the field equation we get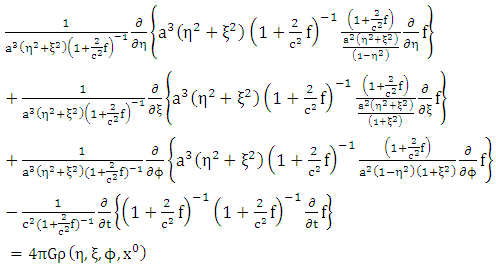 | (1.28) |
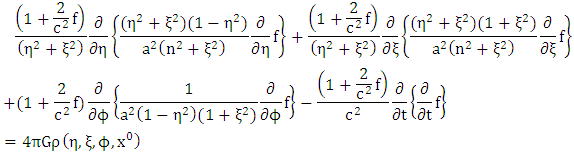 | (1.29) |
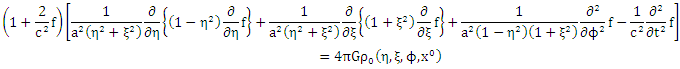 | (1.30) |
Static homogeneous oblate spheroidal distribution of massive bodyNote: (1) No Time variation (static) (2) No azimuthal angle 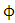 (symmetry)Equation (1.30) reduced to
(symmetry)Equation (1.30) reduced to 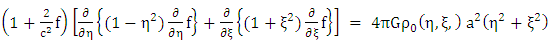 | (1.31) |
Expand: equation (1.31)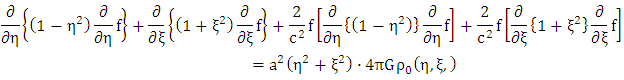 | (1.32) |
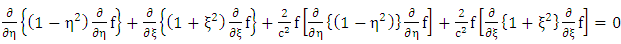 | (1.33) |
Note that: - The first two terms of equation (1.32) are Newton’s gravitational field equations interior to the gravitational scalar potential 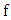 due to a distribution of mass density
due to a distribution of mass density 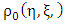 and that of equation (1.33) are Newton’s gravitational field equations exterior with no distribution of mass density.- While the last two terms are the added terms or our contribution due to Riemann and is referred to as Riemann’s gravitational field equation interior and exterior to a static homogeneous oblate spheroid.
and that of equation (1.33) are Newton’s gravitational field equations exterior with no distribution of mass density.- While the last two terms are the added terms or our contribution due to Riemann and is referred to as Riemann’s gravitational field equation interior and exterior to a static homogeneous oblate spheroid.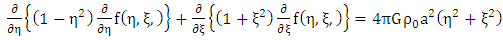 | (1.34) |
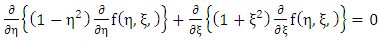 | (1.35) |
Next, let us seek a separable complementary solution of the interior equation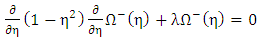 | (1.36) |
 | (1.37) |
where 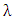 is the separation constants. Consequently, for the choice
is the separation constants. Consequently, for the choice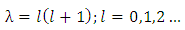 | (1.38) |
equation (1.34) becomes the Legendre’s equation and hence has solution of the form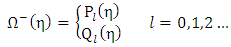 | (1.39) |
where 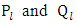 are the linearly independent solutions of the Legendre’s differential equation.Also by the transformation equation
are the linearly independent solutions of the Legendre’s differential equation.Also by the transformation equation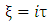 | (1.40) |
equation (1.37) becomes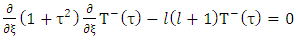 | (1.41) |
This is the Legendre’s differential equation and hence has the solution of the form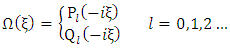 | (1.42) |
Consequently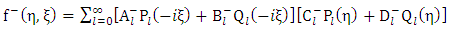 | (1.43) |
where 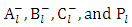 are arbitrary constants. Next let us seek a particular solution of the interior equation
are arbitrary constants. Next let us seek a particular solution of the interior equation 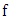 as
as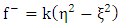 | (1.44) |
substituting equation (1.44) into equation (1.34) it follows that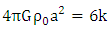 | (1.45) |
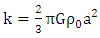 | (1.46) |
Hence the general solution of the interior equation 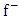 given by:
given by: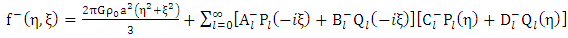 | (1.47) |
Where 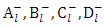 are constants, and
are constants, and 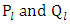 are the Legendre’s functions order
are the Legendre’s functions order 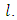 Similarly, since the exterior equation is homogeneous its general solution
Similarly, since the exterior equation is homogeneous its general solution 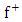 is given by
is given by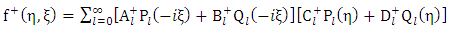 | (1.48) |
Where 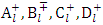 are arbitrary constants. Now since the interior and exterior regions both contain the coordinate
are arbitrary constants. Now since the interior and exterior regions both contain the coordinate 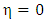 which is a singularity of
which is a singularity of 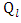
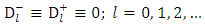 | (1.49) |
Also since 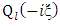 is not defined at the centre of the body
is not defined at the centre of the body 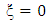 in the interior region
in the interior region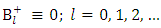 | (1.50) |
Also, since 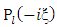 is not defined for
is not defined for 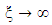 in the exterior region
in the exterior region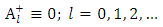 | (1.51) |
Hence from the continuity of the gravitational scalar potentials equations (1.47) and (1.48) across the boundary 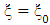 and the orthogonality of the Legendre functions
and the orthogonality of the Legendre functions 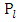 it follows that, the resulting equations are
it follows that, the resulting equations are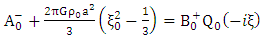 | (1.52) |
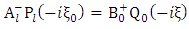 | (1.53) |
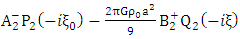 | (1.54) |
From equations (1.52) and (1.54) we get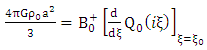 | (1.55) |
and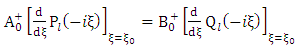 | (1.56) |
Thus solving (1.52)-(1.56) simultaneously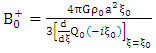 | (1.57) |
and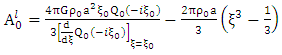 | (1.58) |
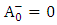 | (1.59) |
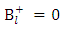 | (1.60) |
Next, let us consider equation (1.54) above i.e.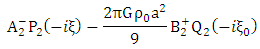 Now differentiate both sides of this equation with respect to
Now differentiate both sides of this equation with respect to 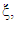 it follow that
it follow that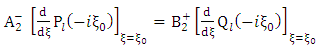 | (1.61) |
By multiplying both sides of equation (1.54) with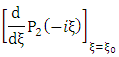 It follows that
It follows that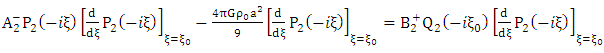 | (1.62) |
This follows by multiplying both side of equation (1.62) with 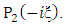 Thus
Thus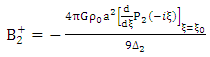 | (1.63) |
where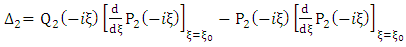 | (1.64) |
And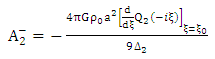 | (1.65) |
Hence the general solution of the interior and exterior equation in equation (1.47) and (1.48) reduce to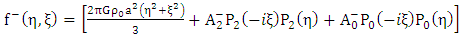 | (1.66) |
and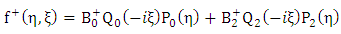 | (1.67) |
These are the gravitational scalar potentials of the body in terms of rest mass density. It follows that gravitational scalar potential (1.66) and (1.67) may be expressed in terms of the total rest mass of the body by the relation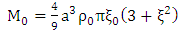 | (1.68) |
It may be noted that results from mathematical tables gives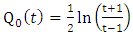 | (1.69) |
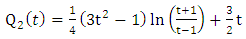 | (1.70) |
Consequently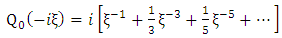 | (1.71) |
and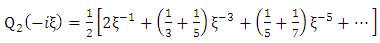 | (1.72) |
3. Summary and Conclusions
In this paper we showed how to formulate the Riemannian Gravitational Field Equation for static homogeneous oblate spheroidal massive bodies using the Riemannian Laplacian operator and golden metric tensor. Also, this paper Newton's gravitational scalar potentials for a homogeneous oblate spheroidal body was formulated and solved with the exact and complete results given by (1.71) and (1.72). Consequently, these potentials are now available for application in physics. A profound philosophical inference is suggested by the results obtained in this paper that Newton's gravitational field equations for a spheroidal body are linear and separable, and hence solvable in terms of the well known special functions of mathematical physics, the Legendre, function. This fact suggests that Einstein's geometrical theory of gravitation, GRT, whose gravitational field equation are non linear may not be the most natural generalization of Newton's dynamical theory of gravitation.It is now known that most bodies in the universe are spheroidal in nature. As an example, it is now well known that satellite orbits around the earth are not governed by just the simple inverse distance squared gravitational fields of perfect spherical geometry. They are also governed by second harmonics (pole of order 3), as well as fourth harmonics (pole of order 5) of gravitational scalar potential due to imperfect spherical geometry. In the first place this paper opens the door for the physical interpretation of all the solutions obtained in this work and hence experimental investigation in the motion of all bodies in the Earth's atmosphere and solar system as well as all other gravitating systems in the universe.In the second place the door in henceforth opened for the mathematical study of all the unsolved equations of motion for all particles in all types of motions in all systems in the universe, such as more accurate calculation of (i) missile and satellite and space craft trajectories in the earth's atmosphere (ii) motions of moons around their planets, (iii) motion of planets (iv) comets and asteroids around the sun and (v) motions of stars around their galactic nuclei in the universe.
References
| [1] | Anderson, J. L. (1967). Principles of Relativity Physics. Academic Press, New York, Pp. 300-472. |
| [2] | Bergmann, P. G. (1987). Introduction to the Theory of Relativity. Prentice Hall India, Pp. 75-240. |
| [3] | Croxton, C. A. Introductory Eigen Physics, John Wiley & sons, London, 1974, PP194-197. |
| [4] | Howusu, S.X.K. (2013). Riemannian Revolution in Physics and Mathematics. Jos University Press Ltd, Jos Pp. 241-244. |
| [5] | Howusu S.X.K. Uduh P. C, Journal of the Nigerian Association of Mathematical physics, 7, 251 – 260. |
| [6] | Howusu S.X.K, Omaghali Y. N and Musongong E. F, Journal of the Nigerian Association of Mathematical Physics, 2004, 142 – 148. |
| [7] | Lumbi, W. L., Howusu, S.X.K. and Liman, M.S. (2014a). Generalized Dynamical Gravitational Field Equation for Static Homogeneous Spherical Massive Distribution of Mass. International Journal of Modern Theoretical Physics 3(1): 37-43. |
| [8] | Howusu, S.X.K. (2013). Riemannian Revolution in Physics and Mathematics. Jos University Press Ltd, Jos Pp. 241-244. |
| [9] | Lumbi, W. L. and Howusu, S.X.K. (2014). Generalized Dynamical Equations of motion for Particles of non-zero Mass for Static Homogeneous Spherical Gravitational Fields. Journal of Nigerian Association of Mathematical Physics, Vol. 27(7): 365-368. |
| [10] | Lumbi, W. L. S.X.K. Howusu, Nuhu Tsaku and Nwagbara O. (2014). Motion of Particles of Non-Zero Rest Masses Exterior to Homogeneous Spherical Mass Distributions. Journal of Nigerian Association of Mathematical Physics, Vol. 27(7): 359-364. |
| [11] | Musongong E.F and Howusu S.X.K, Journal of the Nigerian Association of Mathematical physics 2004, 7, 97 -100. |
| [12] | Morse, H. Feshbach, Method of Theoretical physics, McGrew-Hill, New York, 1953, 21-54. |
| [13] | Weinberg, S. (1972). Principles and Application of the General Theory of Relativity. J. Wiley and Sons, New York, Pp. 3-97. |
| [14] | Stern T. E, Theory of satellite Orbits, Astron, y.1957, 62, 98. |



 The Riemannian dynamical gravitational field equation is given explicitly by [7, 8, 10]
The Riemannian dynamical gravitational field equation is given explicitly by [7, 8, 10]
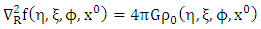
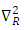 is Riemannian LaplacianGiven
is Riemannian LaplacianGiven 
 is the metric tensor (either schwarztchild or great metric tensor or golden metric tensor). Here we use golden metric tensor of oblate spheroidal coordinates. In spherical polar coordinates, Golden metric tensor is given by:
is the metric tensor (either schwarztchild or great metric tensor or golden metric tensor). Here we use golden metric tensor of oblate spheroidal coordinates. In spherical polar coordinates, Golden metric tensor is given by: 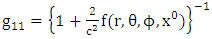
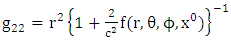
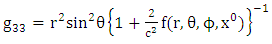
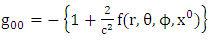
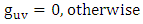
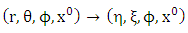 Note that:
Note that: 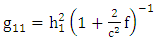
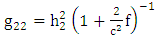
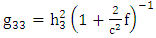
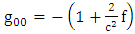
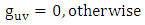
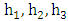 are the scale factors in oblate spheroidal coordinates to be evaluated. Now consider Riemannian Laplacian
are the scale factors in oblate spheroidal coordinates to be evaluated. Now consider Riemannian Laplacian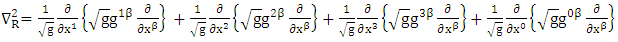
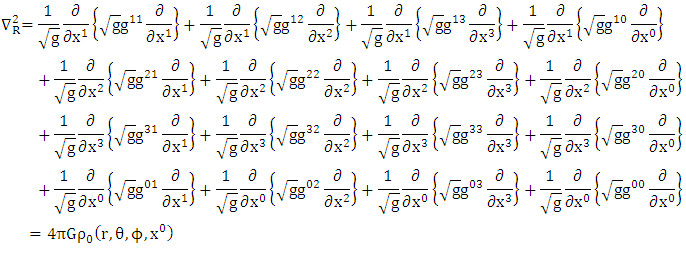
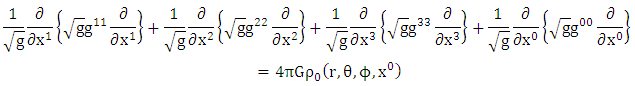
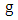 is the determinant of the Golden metric tensor
is the determinant of the Golden metric tensor 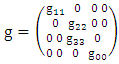
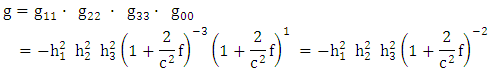
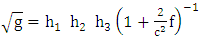
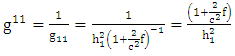
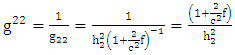
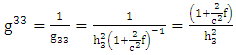
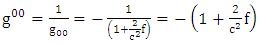
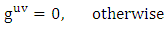
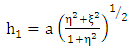
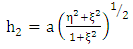
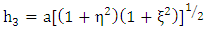
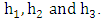 We get:
We get: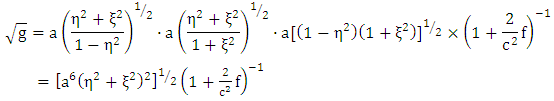
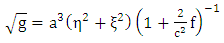
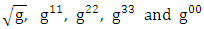 into the field equation we get
into the field equation we get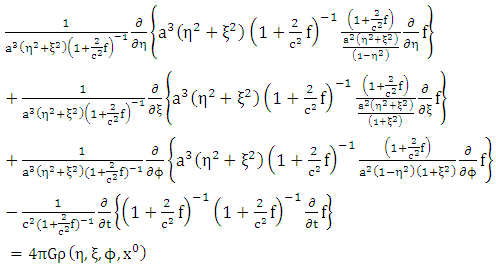
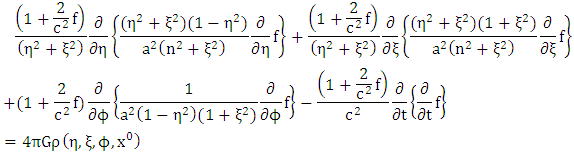
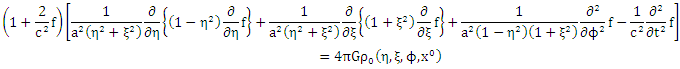
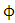 (symmetry)Equation (1.30) reduced to
(symmetry)Equation (1.30) reduced to 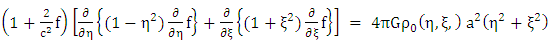
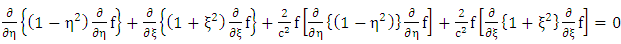
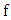 due to a distribution of mass density
due to a distribution of mass density 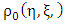 and that of equation (1.33) are Newton’s gravitational field equations exterior with no distribution of mass density.- While the last two terms are the added terms or our contribution due to Riemann and is referred to as Riemann’s gravitational field equation interior and exterior to a static homogeneous oblate spheroid.
and that of equation (1.33) are Newton’s gravitational field equations exterior with no distribution of mass density.- While the last two terms are the added terms or our contribution due to Riemann and is referred to as Riemann’s gravitational field equation interior and exterior to a static homogeneous oblate spheroid.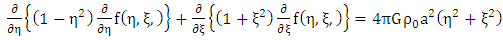
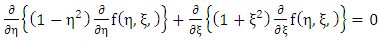
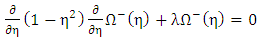

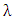 is the separation constants. Consequently, for the choice
is the separation constants. Consequently, for the choice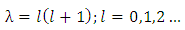
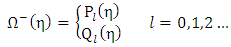
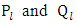 are the linearly independent solutions of the Legendre’s differential equation.Also by the transformation equation
are the linearly independent solutions of the Legendre’s differential equation.Also by the transformation equation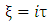
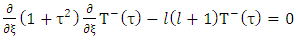
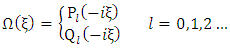
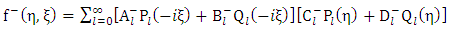
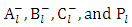 are arbitrary constants. Next let us seek a particular solution of the interior equation
are arbitrary constants. Next let us seek a particular solution of the interior equation 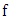 as
as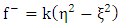
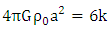
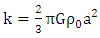
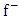 given by:
given by: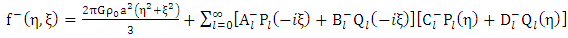
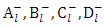 are constants, and
are constants, and 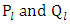 are the Legendre’s functions order
are the Legendre’s functions order 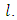 Similarly, since the exterior equation is homogeneous its general solution
Similarly, since the exterior equation is homogeneous its general solution 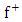 is given by
is given by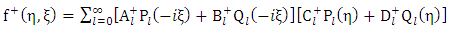
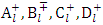 are arbitrary constants. Now since the interior and exterior regions both contain the coordinate
are arbitrary constants. Now since the interior and exterior regions both contain the coordinate  which is a singularity of
which is a singularity of 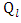
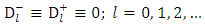
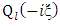 is not defined at the centre of the body
is not defined at the centre of the body 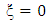 in the interior region
in the interior region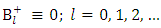
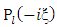 is not defined for
is not defined for 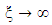 in the exterior region
in the exterior region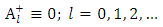
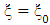 and the orthogonality of the Legendre functions
and the orthogonality of the Legendre functions 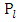 it follows that, the resulting equations are
it follows that, the resulting equations are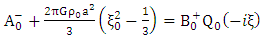
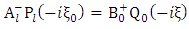
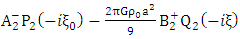
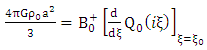
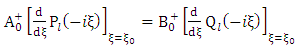
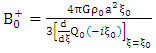
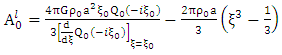
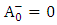
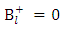
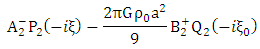 Now differentiate both sides of this equation with respect to
Now differentiate both sides of this equation with respect to 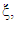 it follow that
it follow that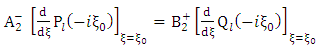
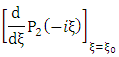 It follows that
It follows that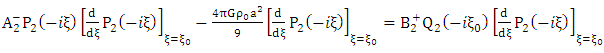
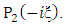 Thus
Thus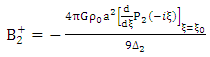
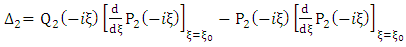
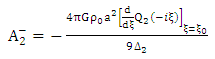
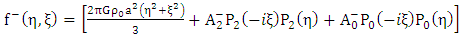
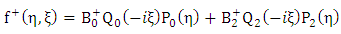
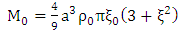
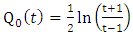
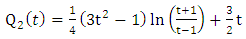
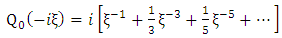
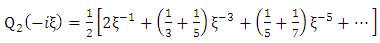
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML