A. A. Adeleke
Department of Physics and Engineering Physics, University of Saskatchewan, Saskatoon, Canada
Correspondence to: A. A. Adeleke, Department of Physics and Engineering Physics, University of Saskatchewan, Saskatoon, Canada.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
The Bloch NMR flow equation was transformed into a porous media based on the condition that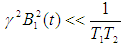 with transformation constant ‘a’ which must be positive. Furthermore, an emerging differential equation along the line was also solved for a physical case where
with transformation constant ‘a’ which must be positive. Furthermore, an emerging differential equation along the line was also solved for a physical case where 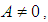 using the method of partial integration. It assumed that the parameter ‘A’ that was a consequence of transforming the fundamental Bloch NMR flow equation into a porous media is not trivial, and thus cannot be ignored. It’s been decades since analysis has been done using the porosity derived on an assumption of triviality of this parameter. The interesting thing about our solution is that it encompasses the solution for a trivial ‘A’ which we believe to be a special case. The solution to this equation is useful in describing physical phenomenon such as permeability and for modelling various other intrinsic factors that affect or influence pore dynamics. The result obtained in this study can have applications in functional magnetic resonance imaging (fMRI), petroleum well design and geological engineering.
using the method of partial integration. It assumed that the parameter ‘A’ that was a consequence of transforming the fundamental Bloch NMR flow equation into a porous media is not trivial, and thus cannot be ignored. It’s been decades since analysis has been done using the porosity derived on an assumption of triviality of this parameter. The interesting thing about our solution is that it encompasses the solution for a trivial ‘A’ which we believe to be a special case. The solution to this equation is useful in describing physical phenomenon such as permeability and for modelling various other intrinsic factors that affect or influence pore dynamics. The result obtained in this study can have applications in functional magnetic resonance imaging (fMRI), petroleum well design and geological engineering.
Keywords:
Bloch NMR equation, Magnetic Resonance Imaging, Porosity, Permeability, Partial Integration
Cite this paper: A. A. Adeleke, Analytical Solution to Fundamental Bloch NMR Flow Equations for Non-Zero Porosity Transformation Parameter, International Journal of Theoretical and Mathematical Physics, Vol. 6 No. 2, 2016, pp. 86-91. doi: 10.5923/j.ijtmp.20160602.04.
1. Introduction
The magnetic properties of nuclei have significant applications in medical imaging and biochemical analysis. These applications are possible because the relaxation properties and the resonance frequency for a nucleus depend upon its environment. Factors such as the presence of chemical bonds, paramagnetic ions, and the rate of flow of fluids influence the magnetic resonance (MR) signal. Therefore, different regions of a biological sample produce different MR signals (Faulkner et al., 2009, Hendee et al., 2003). To investigate the transport process of fluid through a small sized pore, say a nanopore, we have to take the surface porosity of the material into consideration as well as other parameters that are intrinsic to the material (Awojoyogbe etal, 2011). Porosity is a term that is used to describe the extent or degree to which a surface perforated with holes can allow small particles to pass or move through it. Porosity as a property can be explored in the creation of bulk micromachining to fabricate tiny cell-containing chambers within single crystalline silicon wafers. The chambers interface with the surrounding biological environment through polycrystalline silicon filter membranes that are micro machined to present a high density of uniform nanopores as small as 20 nanometres in diameter (Riegler J et al., 2010). These pores are large enough to allow small molecules such as oxygen, glucose, and insulin to pass but are small enough to impede the passage of much larger immune system molecules such as immunoglobulin and graft-borne virus particles (Borchardt et al., 2010). Permeability on the other hand is the ease with which an ion crosses the membrane and is proportional to the total number of open channels for the ion. When two or more ions contribute to the membrane potential, it is likely that the membrane potential would not be at the equilibrium potential for any of the contributing ions. Thus, no ion would be at its equilibrium (i.e., Veq. ≠ Vm). When an ion is not at its equilibrium, an electrochemical driving force (VDF) acts on the ion, causing the net movement of the ion across the membrane down its electrochemical gradient. The driving force is quantified by the difference between the membrane potential and the ion equilibrium potential (VDF = Vm − Veq.) (Awojoyogbe et al, 2002).
2. The NMR Flow Equation
In accordance with Awojoyogbe et.,al, 2009, the time dependent modified Bloch Nuclear magnetic Resonance (NMR) equations could be obtained from: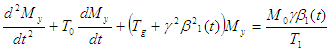 | (1) |
Based on the condition: 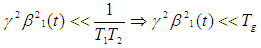 Then equation (1) becomes:
Then equation (1) becomes: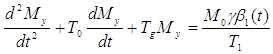 | (2) |
Where 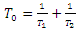 and
and 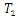 and
and 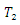 are the Spin-Spin and Spin-Lattice relaxation times respectively.
are the Spin-Spin and Spin-Lattice relaxation times respectively. 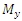 is the Transverse Magnetization,
is the Transverse Magnetization, 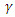 is the gyro-magnetic ratio and
is the gyro-magnetic ratio and 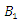 is the external magnetic field.
is the external magnetic field.
3. The Transformation of NMR Transverse Magnetization into a Porous Medium
We apply transformation that will make 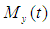 Expressible in term of
Expressible in term of 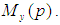 This condition transforms
This condition transforms 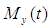 into a porous medium with porosity
into a porous medium with porosity 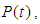 such that by using total differential, we have:
such that by using total differential, we have: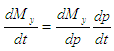 | (3) |
And using the product rule, the second derivative can be derived thus: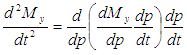 This becomes:
This becomes: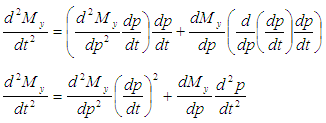 | (4) |
Putting equations 3 and 4 into (2), then we have: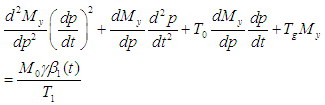 Dividing through by
Dividing through by 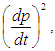 then we can have:
then we can have: 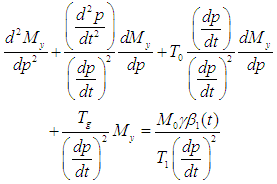 By factorization, we can write that:
By factorization, we can write that: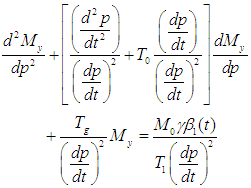 | (5) |
Let 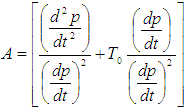 and choosing
and choosing 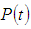 such that:
such that: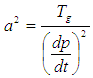 | (6) |
(Awojoyogbe et al., 2009)Putting equation (6) into (5), we have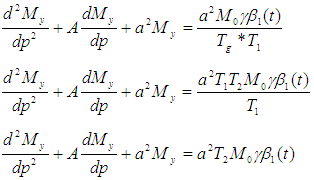 | (7) |
Where: 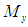 is the Transverse Magnetization
is the Transverse Magnetization 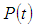 Is the Porosity, ‘a2’ is transformation constant and A is a parameter that can be chosen to be zero or non-zero.
Is the Porosity, ‘a2’ is transformation constant and A is a parameter that can be chosen to be zero or non-zero.
4. Derivation of Porousity
In a quest for exploration evaluation, a solution to equation (6) was presented and dominated Literature. The solution was presented as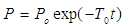 | (8) |
Where 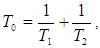 Po is the surface porosity, t is the time constrained to the condition A=0 (Awojoyogbe etal, 2009). However, for years now, it has not been solved for a case where
Po is the surface porosity, t is the time constrained to the condition A=0 (Awojoyogbe etal, 2009). However, for years now, it has not been solved for a case where 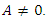 For permeability evaluations, we need to solve equation (6) for a physical case where the parameter A is non-zero and this is non-trivial. In this paper, we are interested in getting the general solution and expression for the equation (6). We start by re-writing equation (6) such that:
For permeability evaluations, we need to solve equation (6) for a physical case where the parameter A is non-zero and this is non-trivial. In this paper, we are interested in getting the general solution and expression for the equation (6). We start by re-writing equation (6) such that: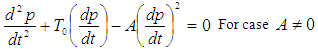 | (9) |
Now we define a term: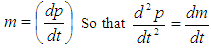 | (10) |
Substituting equation (10) into equation (9) we can write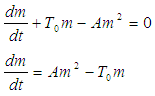 By rearrangement, we have
By rearrangement, we have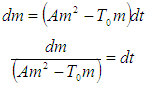 Integrating both sides of the equation, we have:
Integrating both sides of the equation, we have: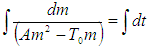 | (11) |
Simplifying the left hand side using partial fraction, then we have: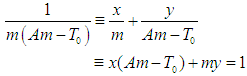 | (12) |
Then we have by equating coefficients that: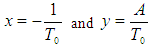 | (13) |
Substituting equation (13) into (12), we have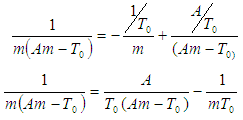 | (14) |
Putting equation (14) back into equation (11)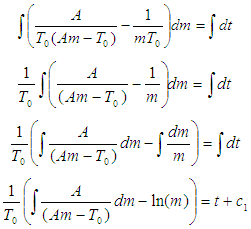 Recalling a general integral rule:
Recalling a general integral rule: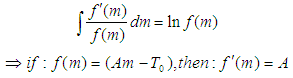 Giving rise to:
Giving rise to: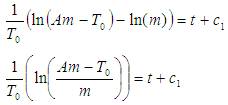 But
But 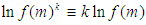 Applying this transformation to the equation above, we have:
Applying this transformation to the equation above, we have: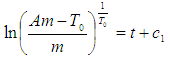 Taking the exponential of both sides, we have:
Taking the exponential of both sides, we have: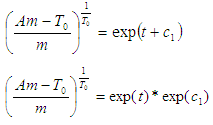 But
But 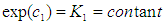
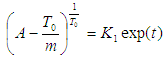 Raising both sides to the power of
Raising both sides to the power of 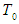
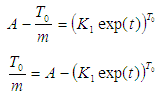 Making m the subject of formula.
Making m the subject of formula.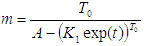 | (15) |
Substuting equation (15) into equation (10), we have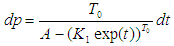 Integrating both sides of the equation
Integrating both sides of the equation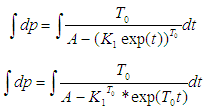 If
If 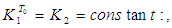 then
then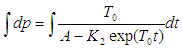 | (16) |
We then define another term: | (17) |
Putting equation (17) into (16), then we have: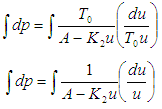 | (18) |
Applying partial fraction to equation (18) above,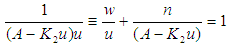 | (19) |
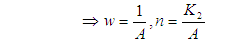 | (20) |
Putting equation (19) and (20) into (18), we have: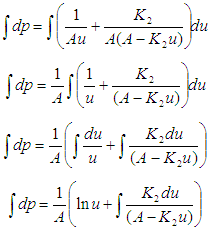 Recall that:
Recall that: 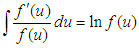
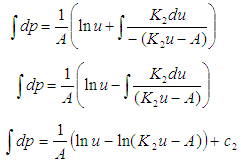 | (21) |
Recalling the value of u from equation (3.50b)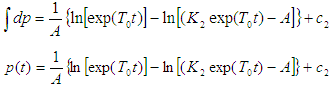 | (22) |
Equation (22) is the general solution of equation (9) that we are trying to solve for  The solution above is the porosity of a porous material as a function of the Magnetic resonance relaxation time (T1 and T2) and the parameter ‘A’, which for many years have been assumed to be zero. The solution above can be a tool to accurately understand the combined effect of the time, relaxation times and the parameter ‘A’ on the dynamics of materials (most especially proteins) through pores. There seems to be evidence to suggest that porosity of a material is not explicitly a function of time only, but something more (Sprawls P., 2000).
The solution above is the porosity of a porous material as a function of the Magnetic resonance relaxation time (T1 and T2) and the parameter ‘A’, which for many years have been assumed to be zero. The solution above can be a tool to accurately understand the combined effect of the time, relaxation times and the parameter ‘A’ on the dynamics of materials (most especially proteins) through pores. There seems to be evidence to suggest that porosity of a material is not explicitly a function of time only, but something more (Sprawls P., 2000).
5. Discussion
A simulation of equation (8) and equation (22) is as shown in figure 1(b) and (a) respectively. The choice of T2 relaxation time was 0.01 sec. which is a typical spin-spin relaxation time for blood flow. Since it was assumed that a nanorobot may move through nanopores as blood will flow through the same porous material (Ottobrini L et al., 2006). From the plot, it is observed that indeed, the parameter ‘A’ has a significant influence on the porosity of a material when imaged through a Magnetic Resonance Imaging (MRI) system. Analysis of equation (8) shows that the porosity P(t) of a nanoporous material varies exponentially with instants of signal sampling and material dependent parameter To, which implies that the porosity of the nanopores decreases at an exponential rate as time of measurement increases, starting from the intrinsic maximum porosity of the material at time t=0 i.e. P(t)=Po. For this research work, Po was chosen to be unity (1). The plot of porosity P(t) was made against time to depict the trend of the decay of porosity experienced. Analysis of equation (22) shows that the porosity P(t) oscillates for T2 relaxation time =0.01 sec while the constant A is chosen to be 5. The porosity was high at an earlier time than 0.2 sec when the oscillation takes place. It is also worthy of note that the presence of parameter ‘A’ has made the porosity to deviate significantly from its intrinsic value at time t close to zero, contrary to what was observed for equation (8). The full wave oscillation was observed between time t=0.2 and 0.4 sec. after which the pore closes up for remaining period of observation. The time t for which porosity become measurable increases from 0 to 0.1 sec. This is a consequence of the function of porosity becoming discontinuous at t=0.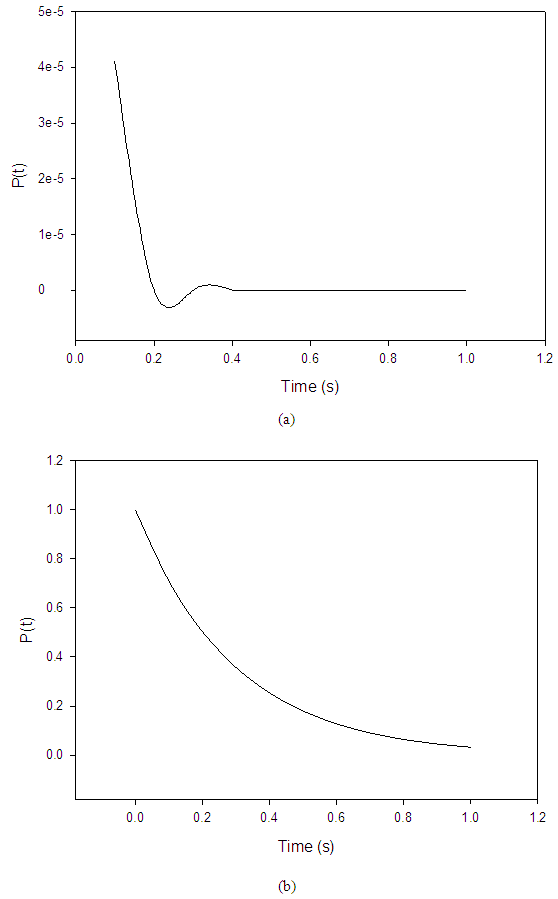 | Figure 1. (a) 2 D graph of P(t) and t(s) for equation (22) for A=5, T2=0.01, (b) 2 D graph of P(t) and t(s) for equation (8) for T2=0.01 |
6. Conclusions
We have obtained basic expression for the porosity of a porous material in the light of Magnetic resonance imaging as a function of time, relaxation times and parameter ‘A’. This general solution is quite interesting in that in it limiting case, as ‘A’ tend to zero; equation (22) converges to equation (8) which is ubiquitous in literature. We have also done a computational analysis to have a feeling of how the two solutions differ. The application of this fundamental solution to solve real life problems related to transport in porous and NMR sensitive media will be presented separately. There, we will propose a possible physical meaning of the parameter ‘A’ and investigate how it affects porosity in combination with other MRI parameters, which is what actually happens in a complex system like human tissue being imaged using MRI.
ACKNOWLEDGEMENTS
The Author is grateful to Dr. Yansun Yao of the Department of Physics and Engineering Physics, University of Saskatchewan, Canada. Also, to both Mr. Dada O.M and Prof. O. B Awojoyogbe of the department of Physics, Federal University of Technology, Minna for their constructive comments.
References
| [1] | Awojoyogbe, Bamidele O., et al. "Computational Diffusion Magnetic Resonance Imaging Based on Time-Dependent Bloch NMR Flow Equation and Bessel Functions." Journal of medical systems 40.4 (2016): 1-14. |
| [2] | Awojoyogbe, O. B., et al. "Mathematical concept of the bloch flow equations for general magnetic resonance imaging: a review." Concepts in Magnetic Resonance Part A 38.3 (2011): 85-101. |
| [3] | Awojoyogbe O. B. (2002). A mathematical model of the Bloch NMR equations for quantitative analysis of blood flow in blood vessels with changing cross section – I. Physica A, 163-175. |
| [4] | Awojoyogbe O. B. (2003). A mathematical model of the Bloch NMR equations for quantitative analysis of blood flow in blood vessels with changing cross section – II. Physica A, 534-550. |
| [5] | Awojoyogbe O. B., Dada M., Faromika O. P., Olufemi F. M., Fuwape O. P. (2009). Polynomial Solutions of Bloch NMR flow equations for classical and quantum mechanical Analysis of fluid flow in porous media. The open Magnetic Resonance Journal, 2(1): 46-56. |
| [6] | Burkhart, Christoph S., Martin Siegemund, and Luzius A. Steiner. "Cerebral perfusion in sepsis." Crit Care 14.2 (2010): 215. |
| [7] | Faulkner K, Mettler Jr, Fred A. "Radiologic and Nuclear Medicine Studies in the United States and Worldwide: Frequency, Radiation Dose, and Comparison with Other Radiation Sources—1950–2007 1." Radiology 253.2 (2009): 520-531. |
| [8] | William R. Hendee Gore, John C., and Robert W. Prost, "Functional MRI is fundamentally limited by an inadequate understanding of the origin of fMRI signals in tissue." Medical physics 30.11 (2003): 2859-2861. |
| [9] | Ottobrini L, Gana P., Bisermi A., Lucignani G., Maggi A., (2006). Molecular Imaging: A new way to study molecular processes invivo. 001 (1): 110 - 112. |
| [10] | Riegler J., Allain B., Cook R. J., Lythgoe M. F., Pankhurt Q. A., (2010). Magnetically Assisted delivery of Cells using a Magnetic Resonsnce Imaging System. 1 (1): 1 – 5. |
| [11] | Sprawls, Perry. Magnetic resonance imaging: principles, methods, and techniques. Medical Physics Publishing, 2000. |


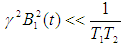 with transformation constant ‘a’ which must be positive. Furthermore, an emerging differential equation along the line was also solved for a physical case where
with transformation constant ‘a’ which must be positive. Furthermore, an emerging differential equation along the line was also solved for a physical case where 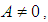 using the method of partial integration. It assumed that the parameter ‘A’ that was a consequence of transforming the fundamental Bloch NMR flow equation into a porous media is not trivial, and thus cannot be ignored. It’s been decades since analysis has been done using the porosity derived on an assumption of triviality of this parameter. The interesting thing about our solution is that it encompasses the solution for a trivial ‘A’ which we believe to be a special case. The solution to this equation is useful in describing physical phenomenon such as permeability and for modelling various other intrinsic factors that affect or influence pore dynamics. The result obtained in this study can have applications in functional magnetic resonance imaging (fMRI), petroleum well design and geological engineering.
using the method of partial integration. It assumed that the parameter ‘A’ that was a consequence of transforming the fundamental Bloch NMR flow equation into a porous media is not trivial, and thus cannot be ignored. It’s been decades since analysis has been done using the porosity derived on an assumption of triviality of this parameter. The interesting thing about our solution is that it encompasses the solution for a trivial ‘A’ which we believe to be a special case. The solution to this equation is useful in describing physical phenomenon such as permeability and for modelling various other intrinsic factors that affect or influence pore dynamics. The result obtained in this study can have applications in functional magnetic resonance imaging (fMRI), petroleum well design and geological engineering.
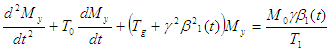
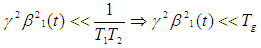 Then equation (1) becomes:
Then equation (1) becomes: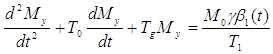
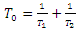 and
and 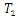 and
and 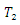 are the Spin-Spin and Spin-Lattice relaxation times respectively.
are the Spin-Spin and Spin-Lattice relaxation times respectively. 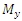 is the Transverse Magnetization,
is the Transverse Magnetization, 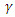 is the gyro-magnetic ratio and
is the gyro-magnetic ratio and 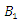 is the external magnetic field.
is the external magnetic field.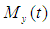 Expressible in term of
Expressible in term of 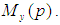 This condition transforms
This condition transforms 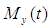 into a porous medium with porosity
into a porous medium with porosity 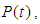 such that by using total differential, we have:
such that by using total differential, we have: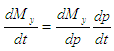
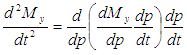 This becomes:
This becomes: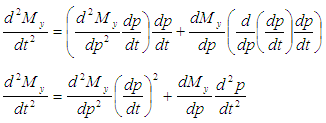
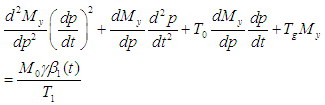 Dividing through by
Dividing through by 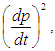 then we can have:
then we can have: 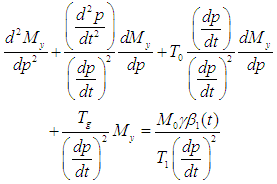 By factorization, we can write that:
By factorization, we can write that: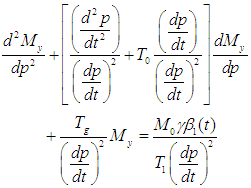
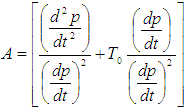 and choosing
and choosing 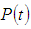 such that:
such that: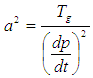
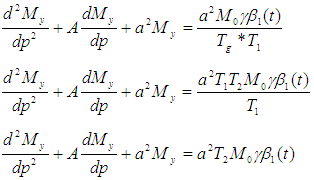
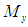 is the Transverse Magnetization
is the Transverse Magnetization 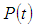 Is the Porosity, ‘a2’ is transformation constant and A is a parameter that can be chosen to be zero or non-zero.
Is the Porosity, ‘a2’ is transformation constant and A is a parameter that can be chosen to be zero or non-zero.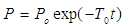
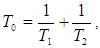 Po is the surface porosity, t is the time constrained to the condition A=0 (Awojoyogbe etal, 2009). However, for years now, it has not been solved for a case where
Po is the surface porosity, t is the time constrained to the condition A=0 (Awojoyogbe etal, 2009). However, for years now, it has not been solved for a case where 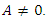 For permeability evaluations, we need to solve equation (6) for a physical case where the parameter A is non-zero and this is non-trivial. In this paper, we are interested in getting the general solution and expression for the equation (6). We start by re-writing equation (6) such that:
For permeability evaluations, we need to solve equation (6) for a physical case where the parameter A is non-zero and this is non-trivial. In this paper, we are interested in getting the general solution and expression for the equation (6). We start by re-writing equation (6) such that: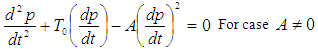
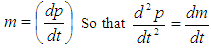
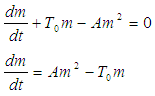 By rearrangement, we have
By rearrangement, we have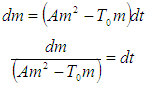 Integrating both sides of the equation, we have:
Integrating both sides of the equation, we have: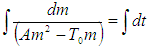
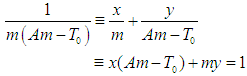
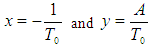
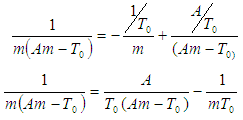
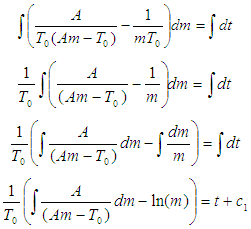 Recalling a general integral rule:
Recalling a general integral rule: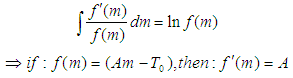 Giving rise to:
Giving rise to: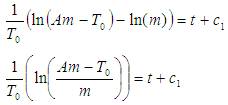 But
But 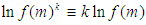 Applying this transformation to the equation above, we have:
Applying this transformation to the equation above, we have: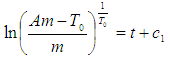 Taking the exponential of both sides, we have:
Taking the exponential of both sides, we have: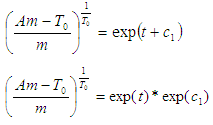 But
But 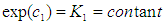
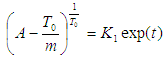 Raising both sides to the power of
Raising both sides to the power of 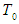
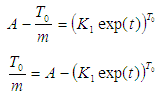 Making m the subject of formula.
Making m the subject of formula.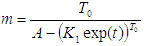
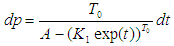 Integrating both sides of the equation
Integrating both sides of the equation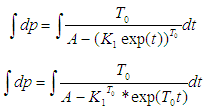 If
If 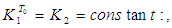 then
then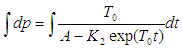

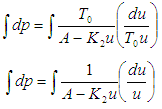
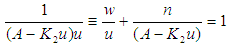
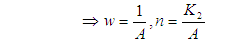
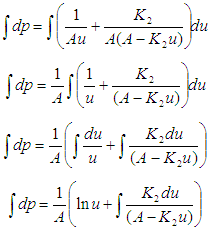 Recall that:
Recall that: 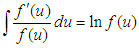
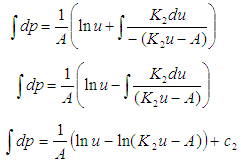
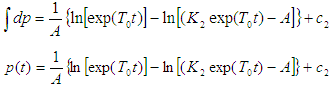
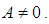 The solution above is the porosity of a porous material as a function of the Magnetic resonance relaxation time (T1 and T2) and the parameter ‘A’, which for many years have been assumed to be zero. The solution above can be a tool to accurately understand the combined effect of the time, relaxation times and the parameter ‘A’ on the dynamics of materials (most especially proteins) through pores. There seems to be evidence to suggest that porosity of a material is not explicitly a function of time only, but something more (Sprawls P., 2000).
The solution above is the porosity of a porous material as a function of the Magnetic resonance relaxation time (T1 and T2) and the parameter ‘A’, which for many years have been assumed to be zero. The solution above can be a tool to accurately understand the combined effect of the time, relaxation times and the parameter ‘A’ on the dynamics of materials (most especially proteins) through pores. There seems to be evidence to suggest that porosity of a material is not explicitly a function of time only, but something more (Sprawls P., 2000).
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML