International Journal of Theoretical and Mathematical Physics

p-ISSN: 2167-6844    e-ISSN: 2167-6852

2016;  6(2): 78-85

doi:10.5923/j.ijtmp.20160602.03

 

Two-Body Problem of Classical Electrodynamics with Radiation Terms − Energy Estimation (III)

Vasil G. Angelov

Department of Mathematics, University of Mining and Geology “St. I. Rilski”, Sofia, Bulgaria

Correspondence to: Vasil G. Angelov, Department of Mathematics, University of Mining and Geology “St. I. Rilski”, Sofia, Bulgaria.

Email:

Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.

This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract

This paper is the third part of our investigations devoted to the two-body problem of classical electrodynamics with radiation terms. The primary purpose of the first part was to derive equations of motion describing two moving charged mass particles with corrected Dirac radiation terms. In the second part we proved an existence-uniqueness of periodic solution of the two-body problem. Here we estimate the energy of the surrounding electron which in particular implies stability of the hydrogen atom. Assuming 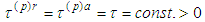we show that radiation parts of the first, second and third equations imply fourth equation (resp. the fifth, sixth and seventh equations imply eighth equation) of motion. The fourth and eighth equations are equations of energy balance. Therefore, estimating the energy of the moving electron, we conclude that the two-body problem is a stable one.

Keywords: Classical relativistic electrodynamics, Two-body problem, Dirac radiation term

Cite this paper: Vasil G. Angelov, Two-Body Problem of Classical Electrodynamics with Radiation Terms − Energy Estimation (III), International Journal of Theoretical and Mathematical Physics, Vol. 6 No. 2, 2016, pp. 78-85. doi: 10.5923/j.ijtmp.20160602.03.

Article Outline

1. Introduction
2. Main Results
    2.1. Transformation of the Radiation Part
    2.2. Energy of the Moving Electron
3. Conclusions

1. Introduction

The present paper is a continuation of the previous two ones [1] and [2], and therefore we will not remind denotations. In [1] we have derived a new form of the Dirac radiation terms and have obtained a new form of the two-body problem equations of motion.
In [2] we have transformed the above equations under Dirac assumption 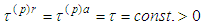and derived a new form of the radiation terms and obtained the existence-uniqueness of the periodic solution.
Here we transform the fourth and eighth equations in an analogous way. To justify the transformation under the above assumption we must show that the fourth equation is a consequence of the transformed first three ones from [2], and similarly the eighth equation is a consequence of the fourth, fifth and sixth equations. Then we estimate the rate of energy of the moving electron in the hydrogen atom which implies its stability.
Let us rewrite the fourth and eighth equations from [1] :
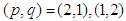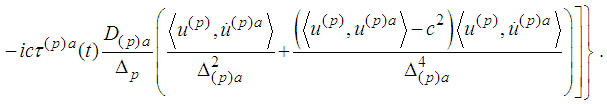The last equations should be divided by 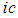, and multiplying by 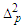we get
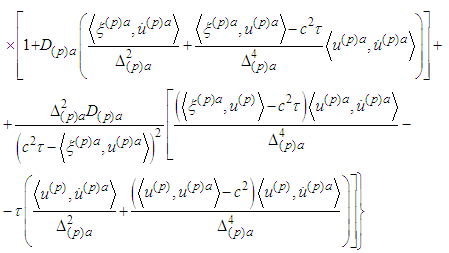
Let us recall that in the above equations the functions 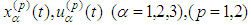are already known.

2. Main Results

2.1. Transformation of the Radiation Part

Using Taylor expansions we obtain
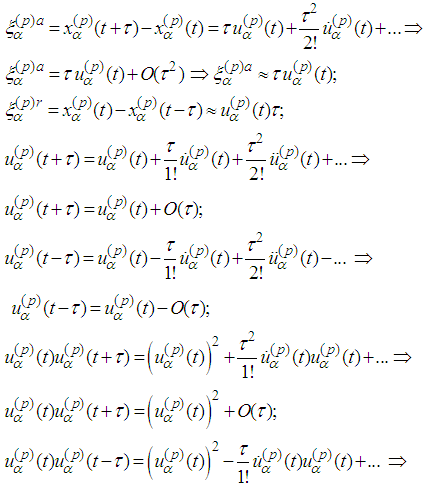
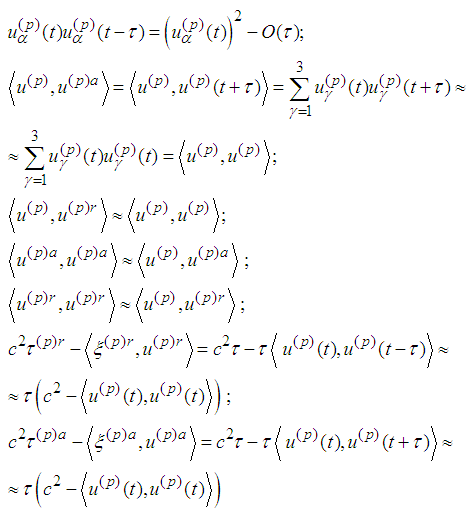and therefore
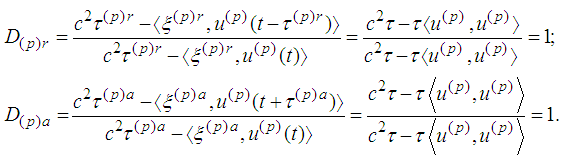Then the radiation parts of the fourth and eighth equations become:
The radiation terms in the equations of motion from [2] are: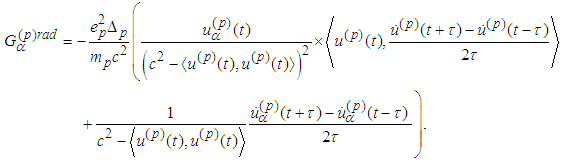
We show that the radiation part of the fourth and eighth equations
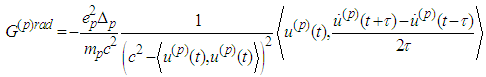can be obtained by .
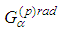Indeed, multiplying the last terms by 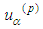and summing up 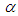we have:
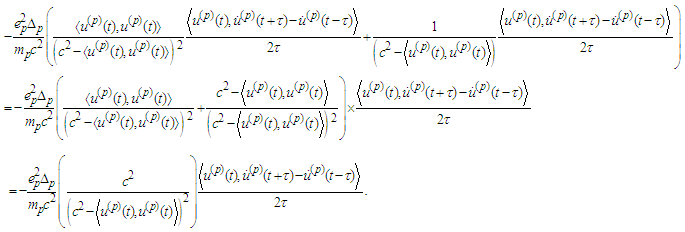Then dividing by we obtain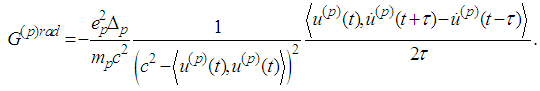

2.2. Energy of the Moving Electron

In view of
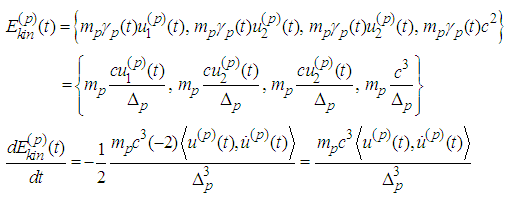We rewrite the above equations in the form
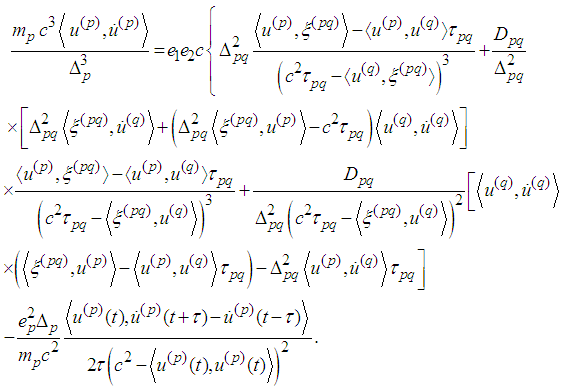We can consider the Kepler problem putting .
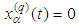From 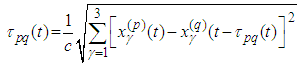we have 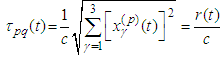and 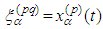. Then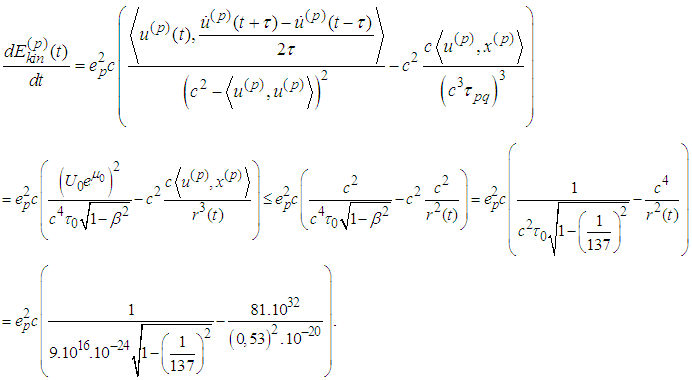

3. Conclusions

Let us estimate the order of every term:
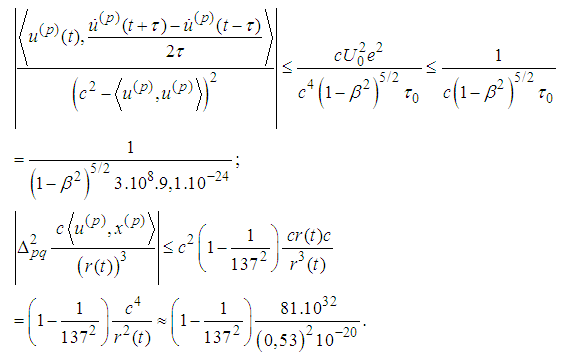Obviously for the first Bohr orbit
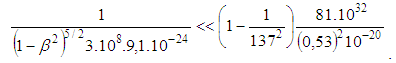This implies that the radiation part of energy is negligibly small and it cannot violate the stability of two-body system (cf. [3]).

References

[1]  Angelov, V. G., 2015, Two-body problem of classical electrodynamics with Dirac radiation terms ̶ Derivation of equations of motion (I). Int. J. Theor. and Math. Phys., 5(5), 119-135.
[2]  Angelov, V. G., 2015, Two-body problem of classical electrodynamics with Dirac radiation terms ̶ existence- uniqueness of a periodic solution (II). Int. J. Theor. and Math. Phys., 6(1), 1-25.
[3]  I. I. Goldenblat and S. W. Ulianov, Introduction to the Relativity Theory and its Applications to the New Technique. Moscow, 1979 (in Russian).