-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2016; 6(2): 75-77
doi:10.5923/j.ijtmp.20160602.02

An Experiment for Light Position in Special Relativity
Andrew Banks
United States
Correspondence to: Andrew Banks, United States.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

An experiment is proposed in Special Relativity (SR) such that two given coordinate systems are in relative motion and a light pulse is emitted from the origins along the positive x-axis when they are common. In a specific configuration of the two coordinate systems, it will be shown that the output of the Lorentz transformations (LT) for the position of light in the primed frame does not match the position of light according to the light postulate (LP) in the primed frame.
Keywords: Special Relativity, Light Postulate, Lorentz Transformations
Cite this paper: Andrew Banks, An Experiment for Light Position in Special Relativity, International Journal of Theoretical and Mathematical Physics, Vol. 6 No. 2, 2016, pp. 75-77. doi: 10.5923/j.ijtmp.20160602.02.
1. Introduction
- The purpose of LT is to correctly translate an event in a source coordinate system to an event in a target coordinate system that is moving in relative motion. Now, since SR is a math theory, it should be expected to provide the mathematical machinery necessary to prove that the LT translation matches what the target frame agrees is true. So for example, given LT translates light event E to E’, other than by blind acceptance. how do we know E’ is actually the correct answer in the primed frame?SR does not lend itself well to such introspection, however any scientific theory should have no problem being subjected to mathematical proof analysis. Now, it is true that the translated light event E’ does measure
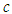 and that can proven mathematically. However, there are many space-time coordinates that measure
and that can proven mathematically. However, there are many space-time coordinates that measure 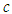 such as
such as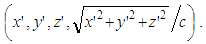 | (1) |
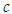 is not a sufficient condition to prove that the primed frame agrees E’ is the correct specific space-time coordinate for the circumstances.This entire analysis depends on the ability to create common agreed upon circumstances for both frames. This can be achieved by considering configurations of the two coordinate systems. So, an experiment is designed below such that the start of the experiment is the configuration where the two origins of the frames are common and a light pulse is emitted from the common origins in the positive direction of the common x-axis. The end of the experiment occurs when the primed coordinate
is not a sufficient condition to prove that the primed frame agrees E’ is the correct specific space-time coordinate for the circumstances.This entire analysis depends on the ability to create common agreed upon circumstances for both frames. This can be achieved by considering configurations of the two coordinate systems. So, an experiment is designed below such that the start of the experiment is the configuration where the two origins of the frames are common and a light pulse is emitted from the common origins in the positive direction of the common x-axis. The end of the experiment occurs when the primed coordinate 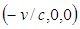 is co-located with the unprimed frame origin.At the end of the experiment, the light pulse is located at some unique position on the positive x-axis of the primed frame coordinates. In the primed frame, the light’s position is determined by LP. In the unprimed frame, the light’s position is first determined by LP and then translated to primed frame coordinates by LT. If the result of LT does not match the primed frame LP result then LT got the answer wrong. The next section gives the details and math for the experiment.
is co-located with the unprimed frame origin.At the end of the experiment, the light pulse is located at some unique position on the positive x-axis of the primed frame coordinates. In the primed frame, the light’s position is determined by LP. In the unprimed frame, the light’s position is first determined by LP and then translated to primed frame coordinates by LT. If the result of LT does not match the primed frame LP result then LT got the answer wrong. The next section gives the details and math for the experiment.2. Experiment
- For the experiment, assume two frames F and F’ are in relative motion in the standard configuration. Assume further when the two origins
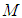 and
and 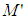 are common, a light pulse is emitted along the common x-axis in the positive direction. Finally assume a primed frame observer is located at
are common, a light pulse is emitted along the common x-axis in the positive direction. Finally assume a primed frame observer is located at 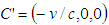 .Now a simple question is proposed. If the coordinate systems are in the configuration such that the origin
.Now a simple question is proposed. If the coordinate systems are in the configuration such that the origin 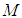 of the F frame and
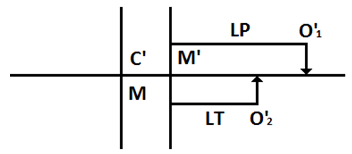
of the F frame and 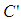 are co-located, which will be named event E, where is the light positioned in the coordinates of the F’ frame? It will be shown that LT calculates an answer that differs from the F’ frame’s light postulate position for the light. See figures 1 and 2 for details.
are co-located, which will be named event E, where is the light positioned in the coordinates of the F’ frame? It will be shown that LT calculates an answer that differs from the F’ frame’s light postulate position for the light. See figures 1 and 2 for details.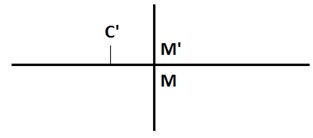 | Figure 1. For the initial conditions, the origins of the two frames are co-located and a light flash is emitted from the two origins along the positive x-axis |
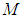 to travel from
to travel from  to
to  while moving at a constant velocity
while moving at a constant velocity 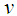 must be determined in order to figure out where the light is located in the F’ frame. Since
must be determined in order to figure out where the light is located in the F’ frame. Since 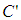 is located at
is located at 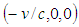 , then the time it takes for
, then the time it takes for 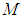 to move from
to move from 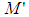 to
to 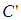 is calculated as follows.
is calculated as follows.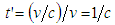 | (2) |
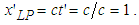 | (3) |
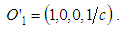 | (4) |
 to travel to
to travel to  must be determined in order to figure out where the light is located in the F frame. Then, we can apply LT to calculate where the light is in the F’ frame.We know the location for
must be determined in order to figure out where the light is located in the F frame. Then, we can apply LT to calculate where the light is in the F’ frame.We know the location for  is
is 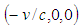 in F’ frame coordinates and obviously
in F’ frame coordinates and obviously 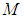 is located at
is located at 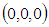 in the F frame. So use the LT
in the F frame. So use the LT 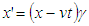 with
with 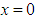 and
and 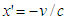 then solve for
then solve for 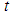 . In that case,
. In that case,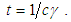 | (5) |
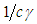 seconds for
seconds for 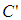 to travel to
to travel to 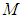 .Now that we have the time in the F frame, apply the light postulate in the F frame. Hence, the light is located in the F frame at
.Now that we have the time in the F frame, apply the light postulate in the F frame. Hence, the light is located in the F frame at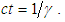 | (6) |
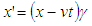 with
with 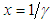 and
and 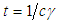 . Then,
. Then,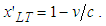 | (7) |
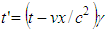 then
then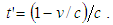 | (8) |
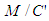 are co-located then according to LT, the light is physically located at the F’ space-time coordinate
are co-located then according to LT, the light is physically located at the F’ space-time coordinate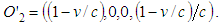 | (9) |
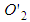 satisfies
satisfies 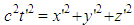 . However, it is different from
. However, it is different from 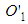 which also satisfies
which also satisfies 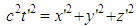 . Therefore given
. Therefore given 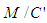 are co-located, the LT calculated space-time position for the light pulse in the coordinates of the F’ frame (equation 9) disagrees with the F’ LP calculated space-time position for the light pulse in the coordinates of the F’ frame (equation 4). Obviously given
are co-located, the LT calculated space-time position for the light pulse in the coordinates of the F’ frame (equation 9) disagrees with the F’ LP calculated space-time position for the light pulse in the coordinates of the F’ frame (equation 4). Obviously given 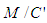 are co-located, one light pulse cannot be located at two different space-time coordinates along the positive x-axis of the F’ frame.One may view the co-location of
are co-located, one light pulse cannot be located at two different space-time coordinates along the positive x-axis of the F’ frame.One may view the co-location of 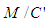 as two different events. Hence, the end of the experiment has different meanings to the two frames and so
as two different events. Hence, the end of the experiment has different meanings to the two frames and so 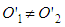 is a correct outcome from this difference. However,
is a correct outcome from this difference. However, 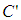 with a time
with a time 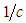 translates to M with a time
translates to M with a time 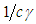 and vice versa. Under SR, that is supposed to mean that they are the same event.If it is argued that
and vice versa. Under SR, that is supposed to mean that they are the same event.If it is argued that 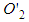 is the valid answer and
is the valid answer and 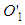 is not then one contradicts the result of the light postulate in the primed frame. Moreover, postulates in a theory are always taken to be true. So, it is not possible to claim
is not then one contradicts the result of the light postulate in the primed frame. Moreover, postulates in a theory are always taken to be true. So, it is not possible to claim 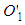 is invalid.If
is invalid.If 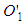 is assumed valid and
is assumed valid and 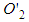 is not then that means there is some problem with LT correctly matching the result of the primed frame light postulate. Finally, one may argue that this discrepancy is a result of the relativity of simultaneity (ROS). Under ROS, since the F’ frame views the events
is not then that means there is some problem with LT correctly matching the result of the primed frame light postulate. Finally, one may argue that this discrepancy is a result of the relativity of simultaneity (ROS). Under ROS, since the F’ frame views the events 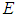 and
and 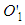 as simultaneous, then the F frame will not. Further, the F frame instead considers
as simultaneous, then the F frame will not. Further, the F frame instead considers 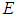 and
and 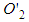 as simultaneous events. Therefore, given
as simultaneous events. Therefore, given 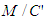 are co-located, it is built within ROS that LT will provide a different location for the light pulse in primed frame coordinates as compared to the primed frame light postulate. So, on one hand assuming ROS
are co-located, it is built within ROS that LT will provide a different location for the light pulse in primed frame coordinates as compared to the primed frame light postulate. So, on one hand assuming ROS 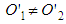 should be the outcome of this experiment. On the other hand, given LT is supposed to provide a correct translation to the truth in the target frame then we expect it to be the case that
should be the outcome of this experiment. On the other hand, given LT is supposed to provide a correct translation to the truth in the target frame then we expect it to be the case that 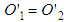 . The demonstration above shows both of these SR requirements cannot be realized from this experiment.
. The demonstration above shows both of these SR requirements cannot be realized from this experiment.3. Conclusions
- This article presented a simple experiment in which it was proven for a specific configuration of two frame coordinates systems, the position of light calculated by LT for the F’ frame did not match the position of light as provided by the F’ light postulate.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML