-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2016; 6(1): 55-57
doi:10.5923/j.ijtmp.20160601.05

Analyzing Time near Horizon in Schwarzschild and De-Sitter Space-Time in Particle’s Frame of Reference
Pravin Kumar Dahal, Narayan Khadka
Trivhuban University, Nepal
Correspondence to: Pravin Kumar Dahal, Trivhuban University, Nepal.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Here, we calculate the variation of distance due to gravitation in De-Sitter and Schwarzschild space. Then, we calculate motion of the particle in particle’s frame of reference to get the result that the particle can’t reach event horizon [r=2GM for Schwarzschild space and r=√ (3/λ) for De-Sitter space] in any frame of reference.
Keywords: Schwarzschild space, De-Sitter space, Length contraction
Cite this paper: Pravin Kumar Dahal, Narayan Khadka, Analyzing Time near Horizon in Schwarzschild and De-Sitter Space-Time in Particle’s Frame of Reference, International Journal of Theoretical and Mathematical Physics, Vol. 6 No. 1, 2016, pp. 55-57. doi: 10.5923/j.ijtmp.20160601.05.
Article Outline
- There have been works on past, from the evolution of general theory of relativity, about the singularity of the Schwarzschild metric. We clearly have,
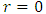 and
and 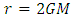 as the singularities in Schwarzschild metric. Since Schwarzschild solution is the solution of Einstein’s field equation in empty space, singularity at
as the singularities in Schwarzschild metric. Since Schwarzschild solution is the solution of Einstein’s field equation in empty space, singularity at 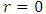 is due to a finite mass concentrated at the point. However, the singularity at
is due to a finite mass concentrated at the point. However, the singularity at 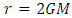 is due to the use of general relativity to describe the physical phenomena and forms the centre of our discussion.Lemaitre [1], Einstein and Rosen [2], Finkelstein [3], Fronsdal [4], Kruskal [5] etc. in past have concluded that the singularity at
is due to the use of general relativity to describe the physical phenomena and forms the centre of our discussion.Lemaitre [1], Einstein and Rosen [2], Finkelstein [3], Fronsdal [4], Kruskal [5] etc. in past have concluded that the singularity at 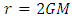 is different from that at
is different from that at 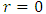 . With the motivation that curvature invariants are perfectly well behaved at
. With the motivation that curvature invariants are perfectly well behaved at 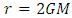 , various efforts have been made by the likes of Lemaitre, Finkelstein, Kruskal etc. to remove the singularity there. However, we might have neglected in past that, for Schwarzschild metric, component of Ricci tensor
, various efforts have been made by the likes of Lemaitre, Finkelstein, Kruskal etc. to remove the singularity there. However, we might have neglected in past that, for Schwarzschild metric, component of Ricci tensor 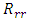 is singular at
is singular at 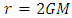 , though it vanishes everywhere else [6]. The tool used to remove the singularity in each of the cases were coordinate transformation, and in every transformation from Schwarzschild metric
, though it vanishes everywhere else [6]. The tool used to remove the singularity in each of the cases were coordinate transformation, and in every transformation from Schwarzschild metric  to
to  there was the situation of either singular or infinite value of some variable at
there was the situation of either singular or infinite value of some variable at 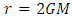 . Although the transformed metric becomes free from singularity, this shouldn’t be thought of as the a great achievement. The two representations
. Although the transformed metric becomes free from singularity, this shouldn’t be thought of as the a great achievement. The two representations 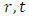 and
and 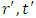 aren’t equivalent representations as the change of parameter isn’t proper i.e. the Jacobian of transformation is either zero or doesn’t exists at
aren’t equivalent representations as the change of parameter isn’t proper i.e. the Jacobian of transformation is either zero or doesn’t exists at 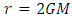 [7]. Hence, this doesn’t inform us whether the singularity is essential singularity or coordinate singularity. In past, we might have focused too much to remove singularity, rather than analyzing the change in space by gravitation in particle’s frame of reference.S. Chandrasekhar [8] had calculated the time taken by the particle to reach the event horizon for Schwarzschild metric, in particle’s frame of reference. However, he didn’t considered the variation of length by Gravitation, and used same elementary length
[7]. Hence, this doesn’t inform us whether the singularity is essential singularity or coordinate singularity. In past, we might have focused too much to remove singularity, rather than analyzing the change in space by gravitation in particle’s frame of reference.S. Chandrasekhar [8] had calculated the time taken by the particle to reach the event horizon for Schwarzschild metric, in particle’s frame of reference. However, he didn’t considered the variation of length by Gravitation, and used same elementary length 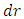 given by Schwarzschild metric, in both non-inertial frame and particle’s frame. The obvious result is the finite value of proper time to reach
given by Schwarzschild metric, in both non-inertial frame and particle’s frame. The obvious result is the finite value of proper time to reach 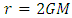 in particle’s frame of reference. Assuming the Principle of Equivalence between gravitation and inertia, variation of length by gravitation is considered in this article to get the result of infinite proper time to reach
in particle’s frame of reference. Assuming the Principle of Equivalence between gravitation and inertia, variation of length by gravitation is considered in this article to get the result of infinite proper time to reach 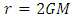 in particle’s frame of reference.For spherically symmetric system with stationary gravitational field, we have the metric calculated by Schwarzschild [9] as;
in particle’s frame of reference.For spherically symmetric system with stationary gravitational field, we have the metric calculated by Schwarzschild [9] as;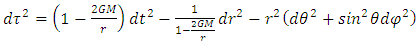 | (1) |
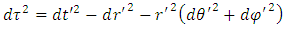 | (2) |
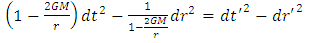 | (3) |
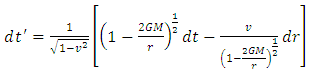 | (4) |
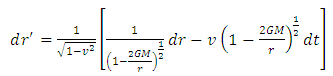 | (5) |
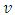 . In the case of gravitation, there exist inertial frame, which is locally inertial frame moving with the particle. Hence,
. In the case of gravitation, there exist inertial frame, which is locally inertial frame moving with the particle. Hence, 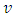 is not constant in the case of gravitation. We can resolve the problem by imagining an infinite no. of inertial systems moving with uniform velocity, one of which instantaneously matches the velocity of the particle [10] i.e. velocity of the particle with respect to the inertial frame is
is not constant in the case of gravitation. We can resolve the problem by imagining an infinite no. of inertial systems moving with uniform velocity, one of which instantaneously matches the velocity of the particle [10] i.e. velocity of the particle with respect to the inertial frame is 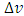 . The particle is thus instantaneously at rest with respect to the inertial systems, which is moving with velocity
. The particle is thus instantaneously at rest with respect to the inertial systems, which is moving with velocity 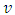 with respect to the given non-inertial frame. Since, velocity of the particle
with respect to the given non-inertial frame. Since, velocity of the particle 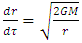 , velocity of our inertial systems varies as
, velocity of our inertial systems varies as 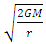 and
and 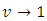 as
as 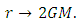 If two frames have their relative velocities zero, i.e. v=0 then from above equations,
If two frames have their relative velocities zero, i.e. v=0 then from above equations,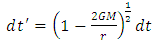 | (6) |
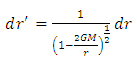 | (7) |

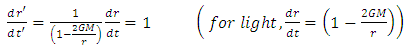 Velocity of light is one in inertial frame of reference. In fact, the transformation rule of the form 4 and 5 is valid not only for Schwarzschild and De-Sitter space-time. But my fellow friend Narayan Khadka has shown, in his unpublished work that, it is in general valid for Kerr and KDS space-time also.Equation 7 gives the variation in length due to gravitation. This equation shows that length gets smaller in non-inertial frame of reference
Velocity of light is one in inertial frame of reference. In fact, the transformation rule of the form 4 and 5 is valid not only for Schwarzschild and De-Sitter space-time. But my fellow friend Narayan Khadka has shown, in his unpublished work that, it is in general valid for Kerr and KDS space-time also.Equation 7 gives the variation in length due to gravitation. This equation shows that length gets smaller in non-inertial frame of reference 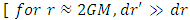 . Similarly, equation 6 gives the relation for time dilation in non-inertial frame of reference.We know that, for radial motion, equation of motion for the particle in Schwarzschild space is,
. Similarly, equation 6 gives the relation for time dilation in non-inertial frame of reference.We know that, for radial motion, equation of motion for the particle in Schwarzschild space is,
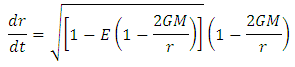
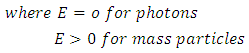 Taking E=1, hereafter, we have,
Taking E=1, hereafter, we have,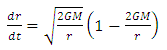 | (8) |
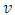 with respect to the frame given by Schwarzschild metric, we have, from equations 4 and 5,
with respect to the frame given by Schwarzschild metric, we have, from equations 4 and 5,
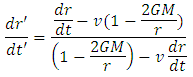
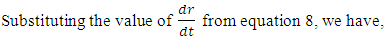

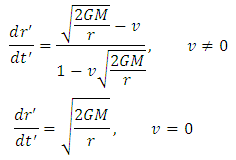 As
As 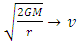 for the particle starting from infinity, we have, from above equation
for the particle starting from infinity, we have, from above equation 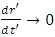 . That is, particle comes to rest in the inertial frame of reference. Now, as
. That is, particle comes to rest in the inertial frame of reference. Now, as 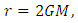
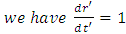 , which is impossible for material particle in inertial frame of reference. Hence, particle doesn’t reach the event horizon in given inertial frame of reference.In particle’s frame of reference,
, which is impossible for material particle in inertial frame of reference. Hence, particle doesn’t reach the event horizon in given inertial frame of reference.In particle’s frame of reference,
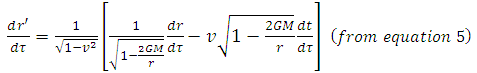
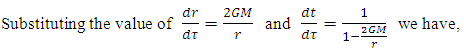
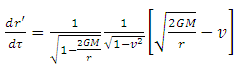 | (9) |
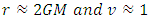 gives,
gives,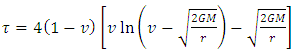 | (10) |
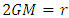 , we have,
, we have, 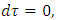 which is impossible for particles having mass. The result of integration 10, from our above argument, clearly diverges as
which is impossible for particles having mass. The result of integration 10, from our above argument, clearly diverges as 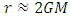 . And, as,
. And, as, 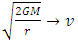 , velocity of the particle
, velocity of the particle 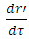 goes to zero.Since,
goes to zero.Since, 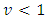 for mass particle, we have,
for mass particle, we have, 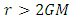 . Hence, the velocity of the particle, in particle’s frame of reference, goes to zero before it reaches the event horizon. Due to the phenomena of length contraction, what we see as a small length in non-inertial frame of reference is very large length in inertial frame of reference. So, the particle takes infinite time
. Hence, the velocity of the particle, in particle’s frame of reference, goes to zero before it reaches the event horizon. Due to the phenomena of length contraction, what we see as a small length in non-inertial frame of reference is very large length in inertial frame of reference. So, the particle takes infinite time 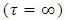 to reach
to reach 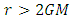 . Thus, in any frame of reference, particle cannot cross
. Thus, in any frame of reference, particle cannot cross 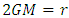 in Schwarzschild space. Similarly, in De-Sitter space, substituting the value
in Schwarzschild space. Similarly, in De-Sitter space, substituting the value 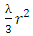 instead of
instead of 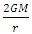 in all of the above equations, where
in all of the above equations, where 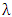 is energy density, we have, for metric,
is energy density, we have, for metric,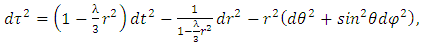 | (11) |

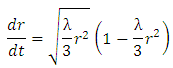 In the inertial frame of reference moving with velocity
In the inertial frame of reference moving with velocity 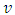 with respect to the non-inertial frame of reference given by equation 10,
with respect to the non-inertial frame of reference given by equation 10,
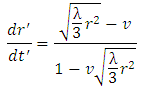 Similarly, in particle’s frame of reference,
Similarly, in particle’s frame of reference,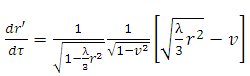 | (12) |
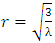 in De-Sitter space. As above, analytical solution of 12 is very complicated. Near
in De-Sitter space. As above, analytical solution of 12 is very complicated. Near 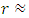
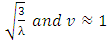 , we have,
, we have,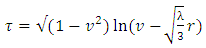 | (13) |
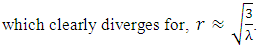
Conclusions
- Hence, we have seen that the event horizon is the region of isolation for the particle in Schwarzschild space and De-Sitter space. Particle can’t cross event horizon in any frame of reference. So, event horizon is the singularity in the particle’s frame of reference also.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML