Estomih S. Massawe
Department of Mathematics, University of Dar es Salaam, Dar es Salaam, Tanzania
Correspondence to: Estomih S. Massawe, Department of Mathematics, University of Dar es Salaam, Dar es Salaam, Tanzania.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this paper it is intended to elaborate a framework in which we can incorporate external forces in the systems prescription with emphasis on Hamiltonian systems with external forces and on the consequences of external forces. An appealing tool for this case is the language of symplectic geometry. Definitions of Hamiltonian systems with external forces are given and it is shown how they fit very naturally into the framework. It is also shown that forces are basic variables and that they have to be included in the definitions of mechanical systems.
Keywords:
Hamiltonian, Control systems, Controllability, Observability
Cite this paper: Estomih S. Massawe, Hamiltonian Control Systems, International Journal of Theoretical and Mathematical Physics, Vol. 6 No. 1, 2016, pp. 26-30. doi: 10.5923/j.ijtmp.20160601.02.
1. Introduction
The dynamics of a system can be formulated using either the Newtonian, the Lagrangian or the Hamiltonian approaches. In the Newtonian and the Lagrangian formulations it is assumed that if all the coordinates and velocities are simultaneously specified, the state of the system can be completely determined and its consequent motion calculated. This gives rise to solving a system of second order ordinary differential equations. On the other hand, the Hamiltonian formulation, we seek to describe the motion in terms of first order equations of motion parametized by generalized coordinates and momenta. The transition from the Newtonian and Lagrangian formulations to the Hamiltonian formulation corresponds to changing the variables in the system from 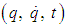 to
to 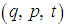 where
where 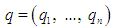 are the generalized coordinates and
are the generalized coordinates and 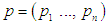 are the generalized momenta [1]. However the Hamiltonian methods are not superior to the other methods for direct solutions of mechanical problems. Rather we gain another more powerful method of working with physical systems. The usefulness of the Hamiltonian viewpoint lies in providing a framework for theoretical extension in many areas of physics such as statistical mechanics and quantum mechanics.A Hamiltonian system is characterized by an existence of a symplectic structure on a smooth even-dimensional manifold [2]. The symplectic approach allows one to extend the local description of a dynamical system to a global description. [3] has shown how network modelling of lumped-parameter physical systems naturally leads to a geometrically defined class of systems, called port-controlled Hamiltonian systems with dissipation. The structural properties of these systems were discussed, in particular the existence of Casimir functions and their implications for stability. [4] has shown the geometric property and structure of the Hamilton--Jacobi equation arising from nonlinear control theory are investigated using symplectic geometry. [5] made an analysis on Hamiltonian systems and his results revealed a systematic geometric frame for generalized controlled Hamiltonian systems. The pseudo-Poisson manifold and the ω-manifold are proposed as the state space of the generalized controlled Hamiltonian systems were established. However the above results did not consider the external forces as basic variables.In this paper it is therefore intended to show that external forces should. It will be shown that it is necessary to maintain forces as basic variables and those have to be included in the definition of mechanical systems.
are the generalized momenta [1]. However the Hamiltonian methods are not superior to the other methods for direct solutions of mechanical problems. Rather we gain another more powerful method of working with physical systems. The usefulness of the Hamiltonian viewpoint lies in providing a framework for theoretical extension in many areas of physics such as statistical mechanics and quantum mechanics.A Hamiltonian system is characterized by an existence of a symplectic structure on a smooth even-dimensional manifold [2]. The symplectic approach allows one to extend the local description of a dynamical system to a global description. [3] has shown how network modelling of lumped-parameter physical systems naturally leads to a geometrically defined class of systems, called port-controlled Hamiltonian systems with dissipation. The structural properties of these systems were discussed, in particular the existence of Casimir functions and their implications for stability. [4] has shown the geometric property and structure of the Hamilton--Jacobi equation arising from nonlinear control theory are investigated using symplectic geometry. [5] made an analysis on Hamiltonian systems and his results revealed a systematic geometric frame for generalized controlled Hamiltonian systems. The pseudo-Poisson manifold and the ω-manifold are proposed as the state space of the generalized controlled Hamiltonian systems were established. However the above results did not consider the external forces as basic variables.In this paper it is therefore intended to show that external forces should. It will be shown that it is necessary to maintain forces as basic variables and those have to be included in the definition of mechanical systems.
2. Hamilton’s Equation
Let 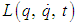 be the Lagrangian function for a given system. Then the Hamiltonian function
be the Lagrangian function for a given system. Then the Hamiltonian function 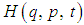 for the system is defined by ([1], [6]).
for the system is defined by ([1], [6]).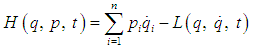 | (1) |
The differential of  is given by
is given by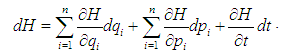 | (2) |
Also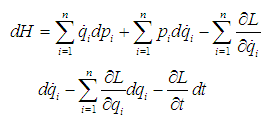 | (3) |
Using 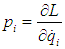 from the generalized momenta, equation (3) reduces to
from the generalized momenta, equation (3) reduces to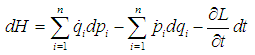 | (4) |
Comparing (4) and (2) we get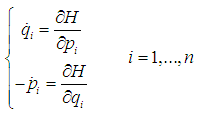 | (5) |
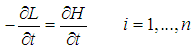 | (6) |
Equations (5) consist of a set of 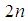 first order ordinary differential equations called the Hamilton’s equations of motion and
first order ordinary differential equations called the Hamilton’s equations of motion and 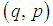 are called canonical coordinates.
are called canonical coordinates.
2.1. Hamiltonian Control Systems
According to [2] we let● 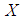 be a manifold
be a manifold 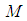 of the state space in a manifold with symplectic form
of the state space in a manifold with symplectic form 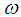 ,●
,● 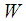 be a manifold of the space of external variables with symplectic form
be a manifold of the space of external variables with symplectic form 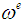 (‘e’ for external). In local coordinates,
(‘e’ for external). In local coordinates, 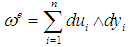 where
where 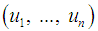 are the external forces (inputs) and
are the external forces (inputs) and 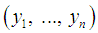 are the observations (outputs),● A fiber bunder
are the observations (outputs),● A fiber bunder 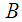 be over
be over 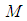 ,● A smooth function (smooth meaning
,● A smooth function (smooth meaning 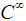 ) such that
) such that 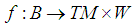 (
( is a tangent bundle over
is a tangent bundle over 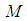 .Then(i)
.Then(i) 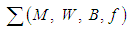 with
with 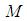 and
and 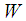 symplectic manifolds is called a full Hamiltonian system if
symplectic manifolds is called a full Hamiltonian system if 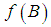 is a Lagrangian submanifold of
is a Lagrangian submanifold of 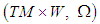 where
where 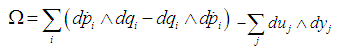 is derived from the local coordinates.(ii)
is derived from the local coordinates.(ii) 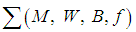 is called degenerate Hamiltonian system if there exists a full Hamiltonian system
is called degenerate Hamiltonian system if there exists a full Hamiltonian system 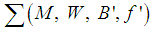 such that
such that 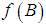 is a submanifold of
is a submanifold of 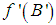 .The definition of Hamiltonian control system depends on the submanifold
.The definition of Hamiltonian control system depends on the submanifold 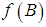 and not on
and not on 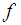 and
and 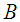 separately. It can be observed that the set of external variables
separately. It can be observed that the set of external variables 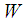 can be split into inputs
can be split into inputs 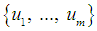 and outputs
and outputs 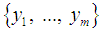 . The inputs are the external forces (controls) and the outputs are the observations. If the external forces are constant, then the dynamics of the system are described by a Hamiltonian vector field on
. The inputs are the external forces (controls) and the outputs are the observations. If the external forces are constant, then the dynamics of the system are described by a Hamiltonian vector field on 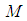 .
.
2.2. Affine Hamiltonian Control Systems
Let 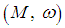 be a symplectic manifold. Let
be a symplectic manifold. Let 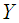 be an observation manifold. Define the symplectic form
be an observation manifold. Define the symplectic form 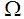 on
on 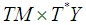 by
by 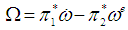 (
(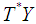 is the cotangent bundle of
is the cotangent bundle of 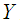 ,
, 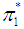 and
and 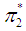 are pullbacks of
are pullbacks of 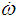 and
and 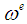 by
by 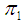 and
and 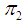 respectively [2]. Then according to [7] an affine Hamiltonian system
respectively [2]. Then according to [7] an affine Hamiltonian system 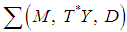 is given by a submanifold
is given by a submanifold 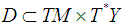 such that(i)
such that(i) 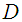 can be parametized by the coordinates of
can be parametized by the coordinates of 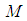 and the coordinates of the fibres of
and the coordinates of the fibres of 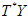 ,(ii)
,(ii) 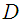 is a Lagrangian submanifold of
is a Lagrangian submanifold of 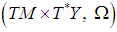 ,(iii) The value of the
,(iii) The value of the 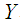 -coordinates of a point on
-coordinates of a point on 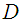 is a function only of the
is a function only of the 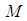 -coordinates of this point.This system is thus given by ([8])
-coordinates of this point.This system is thus given by ([8])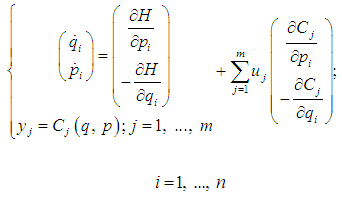 | (7) |
In vector form we denote the system (7) by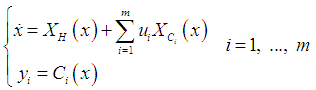 | (8) |
Because of (ii) above, 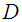 has a generating function. Because of (i) and (ii), this generating function has then form
has a generating function. Because of (i) and (ii), this generating function has then form 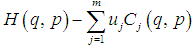 with
with 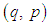 canonical coordinates for
canonical coordinates for 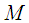 and
and 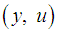 natural coordinates for
natural coordinates for 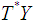 . Therefore
. Therefore 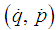 coordinates of
coordinates of 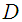 are given by
are given by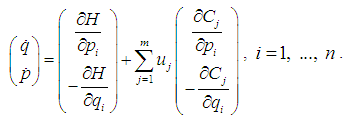 | (9) |
and the 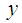 coordinates by
coordinates by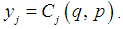 This is equivalent to linearizing
This is equivalent to linearizing 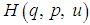 with respect to
with respect to 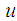 . We note that without condition (iii), the external forces enter the system in a nonlinear way and the generating function of
. We note that without condition (iii), the external forces enter the system in a nonlinear way and the generating function of 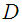 is
is 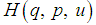 which locally gives
which locally gives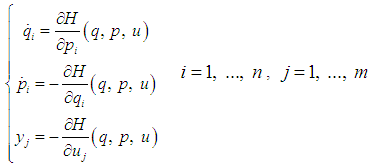 | (10) |
This is just the usual general input-output Hamiltonian system. We note that if there are no dynamics i.e. no state space 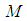 , then
, then 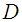 is just a Lagrangian manifold of
is just a Lagrangian manifold of 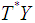 and this describes statistic mechanical systems. If there are no inputs and outputs i.e. no
and this describes statistic mechanical systems. If there are no inputs and outputs i.e. no 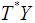 , then
, then 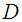 is a Lagrangian submanifold of
is a Lagrangian submanifold of 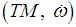 . This describes a locally Hamiltonian vector field.
. This describes a locally Hamiltonian vector field.
2.3. Linear Hamiltonian Control Systems
The Linear system in state form 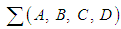 given by
given by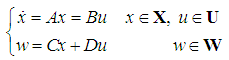 | (11) |
is a linear Hamiltonian system if 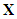 and
and 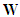 are symplectic linear spaces. It is a result in symplectic geometry that there exists a nondegenerate skew-symmetric bilinear form
are symplectic linear spaces. It is a result in symplectic geometry that there exists a nondegenerate skew-symmetric bilinear form 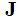 and
and 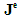 on the state space
on the state space 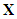 and on the set of external variables
and on the set of external variables 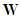 respectively ([2]). In the same language o symplectic geometry if
respectively ([2]). In the same language o symplectic geometry if 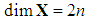 and
and 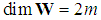 then there exists bases of
then there exists bases of 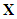 and
and 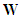 such that in these bases
such that in these bases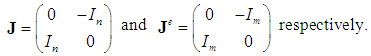 [9] has established and proved by the following theorem the conditions required for the system
[9] has established and proved by the following theorem the conditions required for the system 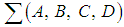 above to be a full linear Hamiltonian system.Theorem 1:Let
above to be a full linear Hamiltonian system.Theorem 1:Let 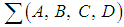 be a linear system given by (11) above. If
be a linear system given by (11) above. If 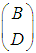 is injective and
is injective and 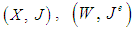 are linear symplectic spaces, then
are linear symplectic spaces, then  is a full Hamiltonian system if
is a full Hamiltonian system if 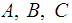 and
and 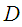 satisfy the following:
satisfy the following: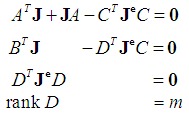 | (11) |
If the feedback given by 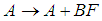 ,
, 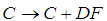 is applied to
is applied to 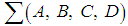 , then necessarily
, then necessarily 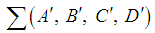 has to satisfy
has to satisfy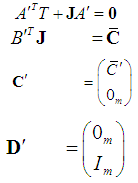 | (12) |
where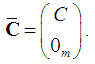 The condition that
The condition that 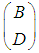 is injective is similar to the condition that
is injective is similar to the condition that 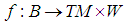 is an embedding for the case of nonlinear systems.
is an embedding for the case of nonlinear systems.
3. Controllability and Observability for Hamiltonian Systems
We shall consider the ideas of controllability and observability only for affine nonlinear Hamiltonian systems. Consider the system given by 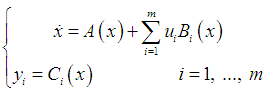 | (13) |
Defined on a symplectic manifold 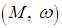 where
where 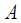 is a locally Hamiltonian vector field i.e. the Lie derivative
is a locally Hamiltonian vector field i.e. the Lie derivative 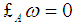 . And
. And 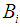 is the Hamiltonian vector fields such that
is the Hamiltonian vector fields such that 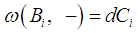 ([10]).Definition 1Consider the affine system (13) above. We define
([10]).Definition 1Consider the affine system (13) above. We define 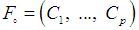 and
and 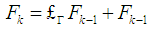 . This system is locally weakly observable if
. This system is locally weakly observable if 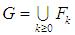 satisfies
satisfies 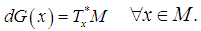 Here
Here 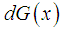 is the linear subspace of
is the linear subspace of 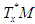 spanned by
spanned by 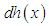 with
with 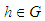 [11].For Hamiltonian systems, since
[11].For Hamiltonian systems, since 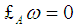 and there exists
and there exists 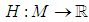 such that
such that 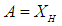 then the
then the 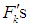 defined above satisfy
defined above satisfy 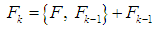 with
with 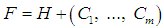 the affine subspace of vector space of functions on
the affine subspace of vector space of functions on 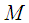 . ([6])We define Controllability and Observability as follows:Controllability: Controllability is the set of points reachable from
. ([6])We define Controllability and Observability as follows:Controllability: Controllability is the set of points reachable from 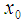 in time
in time 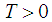 by applying input functions
by applying input functions 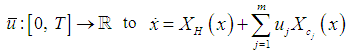 with initial condition
with initial condition 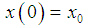 contains an open subset of
contains an open subset of 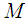 for every
for every 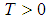 and for every ([9]).Observability: For every
and for every ([9]).Observability: For every 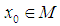 and every
and every 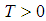 there exists a neighbourhood
there exists a neighbourhood 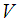 of
of 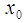 such that for
such that for 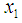 and
and  in
in 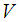 and
and 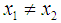 , there exists input functions
, there exists input functions 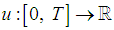 such that, if we denote the solutions of
such that, if we denote the solutions of 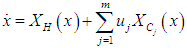 on
on 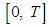 corresponds to initial conditions
corresponds to initial conditions 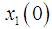 and
and 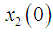 by
by 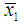 and
and 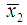 respectively, then the output functions
respectively, then the output functions 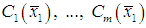 and
and 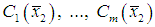 are different while the trajectories
are different while the trajectories 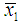 and
and 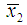 remain in
remain in 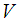 ([9]).
([9]).
4. Feedback for Hamiltonian Systems
Define a function 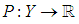 such that
such that 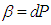 , where
, where 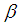 is a closed one-form on the output
is a closed one-form on the output 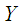 , and consider the output feedback given by
, and consider the output feedback given by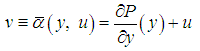 | (14) |
Let 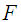 be the graph of
be the graph of 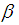 and
and 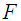 be a Lagrangian submanifold i.e.
be a Lagrangian submanifold i.e. 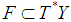 . Accordingly we say that the output feedback given by equation (14) is Hamiltonian ([5]).Proposition 1Let
. Accordingly we say that the output feedback given by equation (14) is Hamiltonian ([5]).Proposition 1Let 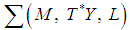 be an affine Hamiltonian system given by
be an affine Hamiltonian system given by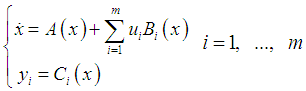 with
with 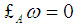 and so
and so 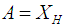 and
and 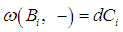 i.e.
i.e. 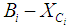 ([5]). Let
([5]). Let 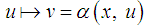 be a feedback for this system. After feedback, this system will again be an affine Hamiltonian system.
be a feedback for this system. After feedback, this system will again be an affine Hamiltonian system.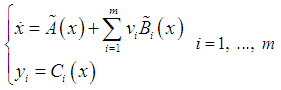 iff
iff 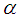 is a Hamiltonian feedback i.e. there exists a function
is a Hamiltonian feedback i.e. there exists a function 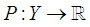 such that
such that 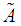 and
and 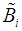 satisfy
satisfy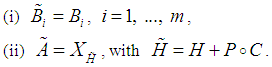 Hence Hamiltonian feedback adds a potential function which is only a function of the output.Let us now consider a solution of Disturbance decoupling by observation feedback (DDOF). The formulation of DDOF is as follows: Let
Hence Hamiltonian feedback adds a potential function which is only a function of the output.Let us now consider a solution of Disturbance decoupling by observation feedback (DDOF). The formulation of DDOF is as follows: Let 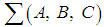 be a Hamiltonian system on a symplectic space
be a Hamiltonian system on a symplectic space 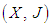 where
where 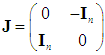 . It is assumed that there are disturbances in this system and it is intended to control the state space. The system can be described by
. It is assumed that there are disturbances in this system and it is intended to control the state space. The system can be described by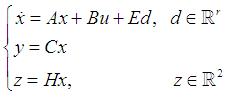 with
with 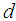 the disturbances and
the disturbances and 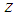 the variables which are to be regulated. We shall call
the variables which are to be regulated. We shall call 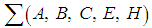 with
with 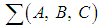 Hamiltonian and
Hamiltonian and 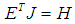 a Hamiltonian system with disturbances. Then the DDOF problem is to find a compensator
a Hamiltonian system with disturbances. Then the DDOF problem is to find a compensator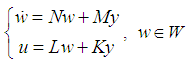 Such that the closed-loop system
Such that the closed-loop system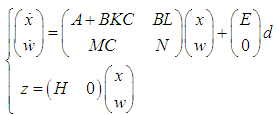 decouples the disturbances
decouples the disturbances 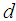 from
from 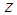 .We shall require
.We shall require 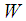 to posses a symplectic form
to posses a symplectic form 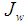 and
and 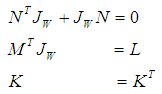 Proposition 2Let
Proposition 2Let  be a Hamiltonian system with disturbances. Then(i) DDOF is solvable iff there exists an
be a Hamiltonian system with disturbances. Then(i) DDOF is solvable iff there exists an 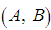 -invariant subspace
-invariant subspace 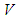 contained in
contained in 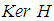 and which is coisotropic ([10]).(ii) DDOF is solvable if the pullback
and which is coisotropic ([10]).(ii) DDOF is solvable if the pullback 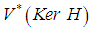 is coisotropic ([7]).Let
is coisotropic ([7]).Let 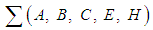 be a Hamiltonian system with disturbances. Let
be a Hamiltonian system with disturbances. Let 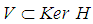 be
be 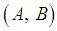 -invariant and Lagrangian, so DDOF is solvable by static output feedback
-invariant and Lagrangian, so DDOF is solvable by static output feedback 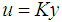 . Then also the Hamiltonian output feedback
. Then also the Hamiltonian output feedback 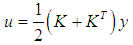 solves DDOF. ([7]).
solves DDOF. ([7]).
5. Discussions and Conclusions
In the past, most treatments in classical mechanics have dealt only with analytical mechanics. This part of mechanics confines itself to the study of mechanical systems without external influences. When forces are present they are assumed as coming from a potential field. In this context one observes the motions, makes classifications etc. i.e. one does only descriptive work but cannot influence the behaviour of the system. This restriction entails a heavy loss of generality because external forces do come up at various places for instance experimental devices and technical applications and mostly cannot be derived from a potential function. Control theory on the other hand does prescriptive work. One attempts to express all models in input/output form so that the variables which may be manipulated and observed are clearly distinguished. Also one tries to find methods for regulating the response of systems by altering the equations of motion. Problems of this type are very natural i.e. in engineering, operational research, and in economics where the problems are laid out in terms of the decision variable (inputs) which have to be chosen on the basis of certain observations (outputs) and the mathematical model involves the interrelations between these variables. The Newtonian and Lagrangian approaches are as good as any other but it is more advantageous to develop the Hamiltonian point of view because it reveals certain structural features e.g. we can anlyze the non-linear systems globally; conservation laws follow easily. In this paper, a framework in which we can incorporate external forces in the systems prescription with emphasis on Hamiltonian systems with external forces and on the consequences of external forces has been elaborated.
References
| [1] | H. Goldestein, Classical Mechanics, Addison-Wesley, Reading, Massachusettes, 1980. |
| [2] | R. A. Abraham, J. E, T. Ratiu, Manifold Tensor Analysis and Applications, 2nd edition, Springer-Verlag, New York, 1988. |
| [3] | A. van der Schaft, Port-controlled Hamiltonian systems: towards a theory for control and design of nonlinear physical systems, Journal of the Society of Instrument and Control Engineers of Japan (SICE), Vol. 39, nr. 2, pp. 91- 98, 2000. |
| [4] | N. Sakomoto, Analysis of the Hamilton--Jacobi Equation in Nonlinear Control Theory by Symplectic Geometry, SIAM Journal on Control and Optimization, Volume 40 Issue 6, 2001, p. 1924 – 1937. |
| [5] | D. Cheng, Z. Xi, Q. Lu, Sh. Mei, Geometric structure of generalized controlled Hamiltonian systems and its application, Science in China Series E: Technological Science, August 2000, Volume 43, Issue 4, p. 365-379. |
| [6] | L. P. Landau and E. M., Lifschitz, Mechanics, Pergamon Press, Oxford, 1976. |
| [7] | A. J., Van der Schaft, “System Theoretic Properties of Hamiltonian Systems with External Forces”, Dynamical Systems and Microphysics Control Theory and Mecanics, pp. 379-399, Academic Press, 1984. |
| [8] | A. J. Van der Schaft, Hamiltonian Dynamics with with External Forces and Observations, Mathematical Systems, SIAM Journal of Control and Optiization, Vol 20, pp. 338-354, 1982. |
| [9] | R. Herman and A.J. Krener, “Nonlinear Controllability and Obervability”, IEEE Trans. Automatic Control, Vol. AC-22, pp. 728-740, 1977. |
| [10] | A. J. Van der Schaft, Disturbances Decoupling by Observation Feedback for Hamiltonian Systems, System and Control Letters,, Vol. 2, pp. 286-291, 1983. |



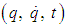 to
to 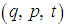 where
where 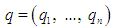 are the generalized coordinates and
are the generalized coordinates and 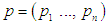 are the generalized momenta [1]. However the Hamiltonian methods are not superior to the other methods for direct solutions of mechanical problems. Rather we gain another more powerful method of working with physical systems. The usefulness of the Hamiltonian viewpoint lies in providing a framework for theoretical extension in many areas of physics such as statistical mechanics and quantum mechanics.A Hamiltonian system is characterized by an existence of a symplectic structure on a smooth even-dimensional manifold [2]. The symplectic approach allows one to extend the local description of a dynamical system to a global description. [3] has shown how network modelling of lumped-parameter physical systems naturally leads to a geometrically defined class of systems, called port-controlled Hamiltonian systems with dissipation. The structural properties of these systems were discussed, in particular the existence of Casimir functions and their implications for stability. [4] has shown the geometric property and structure of the Hamilton--Jacobi equation arising from nonlinear control theory are investigated using symplectic geometry. [5] made an analysis on Hamiltonian systems and his results revealed a systematic geometric frame for generalized controlled Hamiltonian systems. The pseudo-Poisson manifold and the ω-manifold are proposed as the state space of the generalized controlled Hamiltonian systems were established. However the above results did not consider the external forces as basic variables.In this paper it is therefore intended to show that external forces should. It will be shown that it is necessary to maintain forces as basic variables and those have to be included in the definition of mechanical systems.
are the generalized momenta [1]. However the Hamiltonian methods are not superior to the other methods for direct solutions of mechanical problems. Rather we gain another more powerful method of working with physical systems. The usefulness of the Hamiltonian viewpoint lies in providing a framework for theoretical extension in many areas of physics such as statistical mechanics and quantum mechanics.A Hamiltonian system is characterized by an existence of a symplectic structure on a smooth even-dimensional manifold [2]. The symplectic approach allows one to extend the local description of a dynamical system to a global description. [3] has shown how network modelling of lumped-parameter physical systems naturally leads to a geometrically defined class of systems, called port-controlled Hamiltonian systems with dissipation. The structural properties of these systems were discussed, in particular the existence of Casimir functions and their implications for stability. [4] has shown the geometric property and structure of the Hamilton--Jacobi equation arising from nonlinear control theory are investigated using symplectic geometry. [5] made an analysis on Hamiltonian systems and his results revealed a systematic geometric frame for generalized controlled Hamiltonian systems. The pseudo-Poisson manifold and the ω-manifold are proposed as the state space of the generalized controlled Hamiltonian systems were established. However the above results did not consider the external forces as basic variables.In this paper it is therefore intended to show that external forces should. It will be shown that it is necessary to maintain forces as basic variables and those have to be included in the definition of mechanical systems.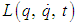 be the Lagrangian function for a given system. Then the Hamiltonian function
be the Lagrangian function for a given system. Then the Hamiltonian function 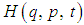 for the system is defined by ([1], [6]).
for the system is defined by ([1], [6]).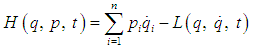
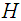 is given by
is given by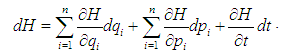
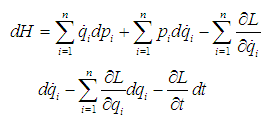
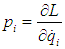 from the generalized momenta, equation (3) reduces to
from the generalized momenta, equation (3) reduces to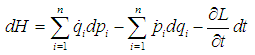
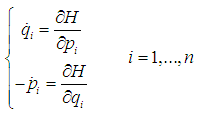
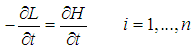
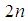 first order ordinary differential equations called the Hamilton’s equations of motion and
first order ordinary differential equations called the Hamilton’s equations of motion and 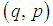 are called canonical coordinates.
are called canonical coordinates.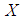 be a manifold
be a manifold 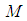 of the state space in a manifold with symplectic form
of the state space in a manifold with symplectic form 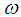 ,●
,● 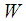 be a manifold of the space of external variables with symplectic form
be a manifold of the space of external variables with symplectic form 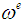 (‘e’ for external). In local coordinates,
(‘e’ for external). In local coordinates, 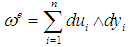 where
where 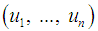 are the external forces (inputs) and
are the external forces (inputs) and 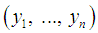 are the observations (outputs),● A fiber bunder
are the observations (outputs),● A fiber bunder 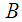 be over
be over 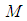 ,● A smooth function (smooth meaning
,● A smooth function (smooth meaning 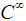 ) such that
) such that 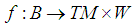 (
(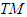 is a tangent bundle over
is a tangent bundle over 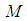 .Then(i)
.Then(i) 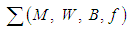 with
with 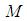 and
and 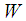 symplectic manifolds is called a full Hamiltonian system if
symplectic manifolds is called a full Hamiltonian system if 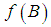 is a Lagrangian submanifold of
is a Lagrangian submanifold of 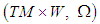 where
where 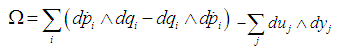 is derived from the local coordinates.(ii)
is derived from the local coordinates.(ii) 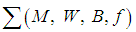 is called degenerate Hamiltonian system if there exists a full Hamiltonian system
is called degenerate Hamiltonian system if there exists a full Hamiltonian system 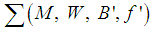 such that
such that 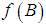 is a submanifold of
is a submanifold of 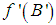 .The definition of Hamiltonian control system depends on the submanifold
.The definition of Hamiltonian control system depends on the submanifold 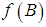 and not on
and not on 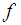 and
and 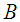 separately. It can be observed that the set of external variables
separately. It can be observed that the set of external variables 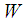 can be split into inputs
can be split into inputs 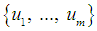 and outputs
and outputs 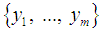 . The inputs are the external forces (controls) and the outputs are the observations. If the external forces are constant, then the dynamics of the system are described by a Hamiltonian vector field on
. The inputs are the external forces (controls) and the outputs are the observations. If the external forces are constant, then the dynamics of the system are described by a Hamiltonian vector field on 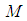 .
.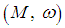 be a symplectic manifold. Let
be a symplectic manifold. Let 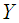 be an observation manifold. Define the symplectic form
be an observation manifold. Define the symplectic form 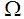 on
on 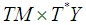 by
by 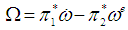 (
(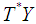 is the cotangent bundle of
is the cotangent bundle of 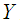 ,
, 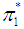 and
and 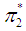 are pullbacks of
are pullbacks of 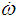 and
and 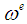 by
by 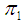 and
and 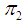 respectively [2]. Then according to [7] an affine Hamiltonian system
respectively [2]. Then according to [7] an affine Hamiltonian system 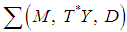 is given by a submanifold
is given by a submanifold 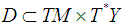 such that(i)
such that(i) 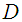 can be parametized by the coordinates of
can be parametized by the coordinates of 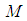 and the coordinates of the fibres of
and the coordinates of the fibres of 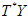 ,(ii)
,(ii) 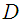 is a Lagrangian submanifold of
is a Lagrangian submanifold of 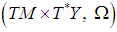 ,(iii) The value of the
,(iii) The value of the 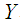 -coordinates of a point on
-coordinates of a point on 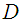 is a function only of the
is a function only of the 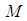 -coordinates of this point.This system is thus given by ([8])
-coordinates of this point.This system is thus given by ([8])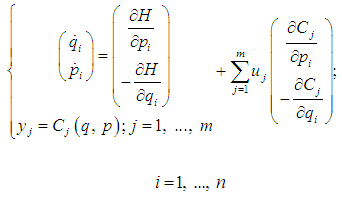
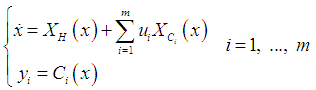
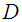 has a generating function. Because of (i) and (ii), this generating function has then form
has a generating function. Because of (i) and (ii), this generating function has then form 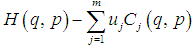 with
with 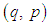 canonical coordinates for
canonical coordinates for 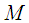 and
and 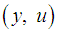 natural coordinates for
natural coordinates for 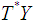 . Therefore
. Therefore 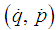 coordinates of
coordinates of 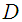 are given by
are given by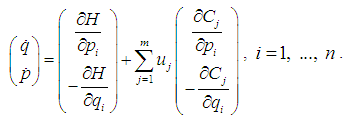
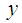 coordinates by
coordinates by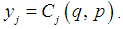 This is equivalent to linearizing
This is equivalent to linearizing 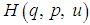 with respect to
with respect to 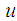 . We note that without condition (iii), the external forces enter the system in a nonlinear way and the generating function of
. We note that without condition (iii), the external forces enter the system in a nonlinear way and the generating function of 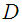 is
is 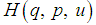 which locally gives
which locally gives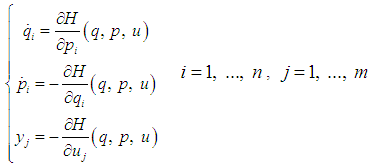
 , then
, then  is just a Lagrangian manifold of
is just a Lagrangian manifold of  and this describes statistic mechanical systems. If there are no inputs and outputs i.e. no
and this describes statistic mechanical systems. If there are no inputs and outputs i.e. no 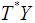 , then
, then 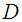 is a Lagrangian submanifold of
is a Lagrangian submanifold of 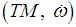 . This describes a locally Hamiltonian vector field.
. This describes a locally Hamiltonian vector field.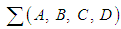 given by
given by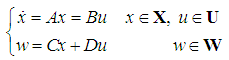
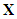 and
and 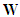 are symplectic linear spaces. It is a result in symplectic geometry that there exists a nondegenerate skew-symmetric bilinear form
are symplectic linear spaces. It is a result in symplectic geometry that there exists a nondegenerate skew-symmetric bilinear form 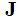 and
and 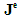 on the state space
on the state space 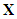 and on the set of external variables
and on the set of external variables 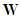 respectively ([2]). In the same language o symplectic geometry if
respectively ([2]). In the same language o symplectic geometry if 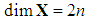 and
and 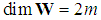 then there exists bases of
then there exists bases of 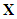 and
and 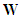 such that in these bases
such that in these bases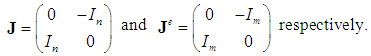 [9] has established and proved by the following theorem the conditions required for the system
[9] has established and proved by the following theorem the conditions required for the system 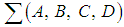 above to be a full linear Hamiltonian system.Theorem 1:Let
above to be a full linear Hamiltonian system.Theorem 1:Let 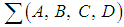 be a linear system given by (11) above. If
be a linear system given by (11) above. If 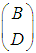 is injective and
is injective and 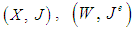 are linear symplectic spaces, then
are linear symplectic spaces, then 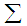 is a full Hamiltonian system if
is a full Hamiltonian system if 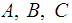 and
and  satisfy the following:
satisfy the following: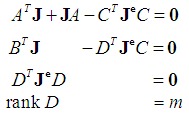
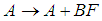 ,
, 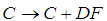 is applied to
is applied to 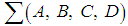 , then necessarily
, then necessarily 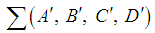 has to satisfy
has to satisfy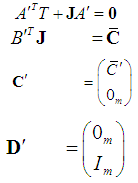
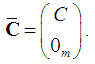 The condition that
The condition that 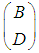 is injective is similar to the condition that
is injective is similar to the condition that  is an embedding for the case of nonlinear systems.
is an embedding for the case of nonlinear systems.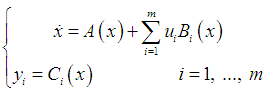
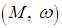 where
where 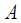 is a locally Hamiltonian vector field i.e. the Lie derivative
is a locally Hamiltonian vector field i.e. the Lie derivative 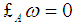 . And
. And 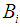 is the Hamiltonian vector fields such that
is the Hamiltonian vector fields such that 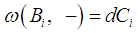 ([10]).Definition 1Consider the affine system (13) above. We define
([10]).Definition 1Consider the affine system (13) above. We define 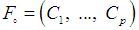 and
and 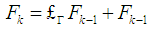 . This system is locally weakly observable if
. This system is locally weakly observable if 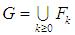 satisfies
satisfies 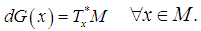 Here
Here 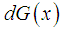 is the linear subspace of
is the linear subspace of 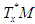 spanned by
spanned by 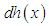 with
with 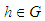 [11].For Hamiltonian systems, since
[11].For Hamiltonian systems, since 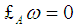 and there exists
and there exists 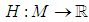 such that
such that 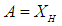 then the
then the 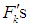 defined above satisfy
defined above satisfy 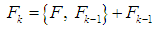 with
with 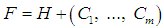 the affine subspace of vector space of functions on
the affine subspace of vector space of functions on 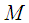 . ([6])We define Controllability and Observability as follows:Controllability: Controllability is the set of points reachable from
. ([6])We define Controllability and Observability as follows:Controllability: Controllability is the set of points reachable from 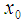 in time
in time 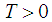 by applying input functions
by applying input functions 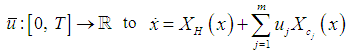 with initial condition
with initial condition 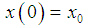 contains an open subset of
contains an open subset of 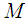 for every
for every 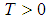 and for every ([9]).Observability: For every
and for every ([9]).Observability: For every 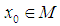 and every
and every 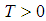 there exists a neighbourhood
there exists a neighbourhood 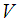 of
of 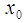 such that for
such that for 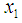 and
and  in
in 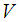 and
and 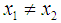 , there exists input functions
, there exists input functions 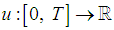 such that, if we denote the solutions of
such that, if we denote the solutions of 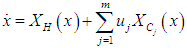 on
on 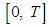 corresponds to initial conditions
corresponds to initial conditions 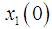 and
and 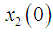 by
by 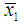 and
and 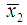 respectively, then the output functions
respectively, then the output functions 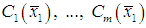 and
and 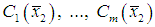 are different while the trajectories
are different while the trajectories 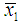 and
and 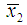 remain in
remain in 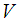 ([9]).
([9]).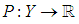 such that
such that 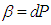 , where
, where 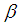 is a closed one-form on the output
is a closed one-form on the output 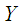 , and consider the output feedback given by
, and consider the output feedback given by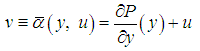
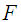 be the graph of
be the graph of 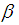 and
and 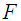 be a Lagrangian submanifold i.e.
be a Lagrangian submanifold i.e. 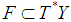 . Accordingly we say that the output feedback given by equation (14) is Hamiltonian ([5]).Proposition 1Let
. Accordingly we say that the output feedback given by equation (14) is Hamiltonian ([5]).Proposition 1Let 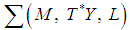 be an affine Hamiltonian system given by
be an affine Hamiltonian system given by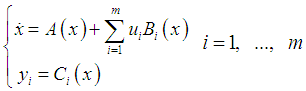 with
with 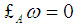 and so
and so 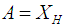 and
and 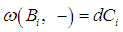 i.e.
i.e. 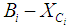 ([5]). Let
([5]). Let 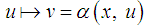 be a feedback for this system. After feedback, this system will again be an affine Hamiltonian system.
be a feedback for this system. After feedback, this system will again be an affine Hamiltonian system.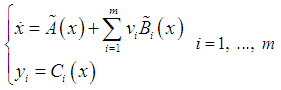 iff
iff 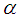 is a Hamiltonian feedback i.e. there exists a function
is a Hamiltonian feedback i.e. there exists a function 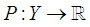 such that
such that 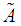 and
and 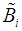 satisfy
satisfy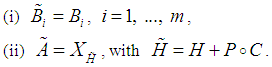 Hence Hamiltonian feedback adds a potential function which is only a function of the output.Let us now consider a solution of Disturbance decoupling by observation feedback (DDOF). The formulation of DDOF is as follows: Let
Hence Hamiltonian feedback adds a potential function which is only a function of the output.Let us now consider a solution of Disturbance decoupling by observation feedback (DDOF). The formulation of DDOF is as follows: Let 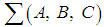 be a Hamiltonian system on a symplectic space
be a Hamiltonian system on a symplectic space 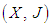 where
where 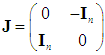 . It is assumed that there are disturbances in this system and it is intended to control the state space. The system can be described by
. It is assumed that there are disturbances in this system and it is intended to control the state space. The system can be described by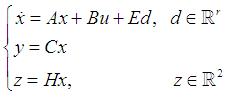 with
with 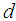 the disturbances and
the disturbances and 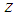 the variables which are to be regulated. We shall call
the variables which are to be regulated. We shall call 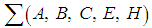 with
with 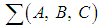 Hamiltonian and
Hamiltonian and 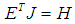 a Hamiltonian system with disturbances. Then the DDOF problem is to find a compensator
a Hamiltonian system with disturbances. Then the DDOF problem is to find a compensator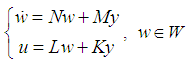 Such that the closed-loop system
Such that the closed-loop system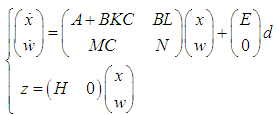 decouples the disturbances
decouples the disturbances 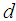 from
from 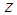 .We shall require
.We shall require 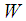 to posses a symplectic form
to posses a symplectic form 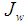 and
and 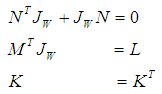 Proposition 2Let
Proposition 2Let 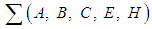 be a Hamiltonian system with disturbances. Then(i) DDOF is solvable iff there exists an
be a Hamiltonian system with disturbances. Then(i) DDOF is solvable iff there exists an 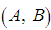 -invariant subspace
-invariant subspace 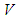 contained in
contained in 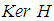 and which is coisotropic ([10]).(ii) DDOF is solvable if the pullback
and which is coisotropic ([10]).(ii) DDOF is solvable if the pullback 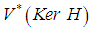 is coisotropic ([7]).Let
is coisotropic ([7]).Let 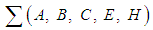 be a Hamiltonian system with disturbances. Let
be a Hamiltonian system with disturbances. Let 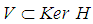 be
be 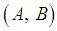 -invariant and Lagrangian, so DDOF is solvable by static output feedback
-invariant and Lagrangian, so DDOF is solvable by static output feedback 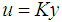 . Then also the Hamiltonian output feedback
. Then also the Hamiltonian output feedback 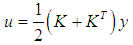 solves DDOF. ([7]).
solves DDOF. ([7]). Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML