-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2016; 6(1): 1-25
doi:10.5923/j.ijtmp.20160601.01

Two-Body Problem of Classical Electrodynamics with Radiation Terms - Periodic Solution (II)
Vasil G. Angelov
Department of Mathematics, University of Mining and Geology “St. I. Rilski”, Sofia, Bulgaria
Correspondence to: Vasil G. Angelov , Department of Mathematics, University of Mining and Geology “St. I. Rilski”, Sofia, Bulgaria.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

This paper is the second in a series of papers dedicated to the two-body problem of classical electrodynamics. In the first part we have derived equations of motion describing two-body problem of classical electrodynamics with radiation terms based on W. Pauli, J. L. Synge and P. A. M. Dirac results. The system obtained is a neutral one with respect to the unknown velocities with both retarded and advanced arguments depending on the unknown trajectories. We introduce a suitable operator whose fixed point is a periodic solution of the problem in question. Using fixed point theorem we prove the main result. Since we consider two charged particles in an internal frame of reference, we prove an existence-unique- ness of a periodic solution that implies an existence of closed orbits. In other words N. Bohr stationary states are a consequence of classical electrodynamics. We generalize A. Sommerfeld result where he has proved an existence of elliptic orbits of the classical Kepler problem. Our existence result gives also a method of overcoming the singularities.
Keywords: Two-Body problem, Dirac radiation term, Neutral equations, Periodic solution, Fixed point theorem
Cite this paper: Vasil G. Angelov , Two-Body Problem of Classical Electrodynamics with Radiation Terms - Periodic Solution (II), International Journal of Theoretical and Mathematical Physics, Vol. 6 No. 1, 2016, pp. 1-25. doi: 10.5923/j.ijtmp.20160601.01.
Article Outline
1. Introduction
- The primary goal of the present paper is to prove an existence-uniqueness of a periodic solution of the two-body system with radiation terms, derived in a recent paper [1]. We have already mentioned in [1] that using the relativistic form of Lienard-Wiechert retarded potentials (cf. [2]) J. L. Synge [3] has formulated the two-body problem of classical electrodynamics and has suggested the idea to generalize the model including Dirac radiation terms [4]. Developing Synge idea we have derived a new form of Dirac radiation terms [1]. So instead of Synge two-body system [2]
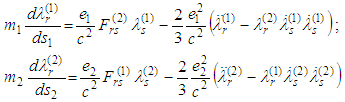 we have introduced the system
we have introduced the system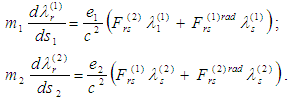 where the radiation terms
where the radiation terms 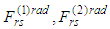 have a new form, although
have a new form, although 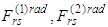 are derived on the basis of the original Dirac physical assumptions [4]. In [1] we have proved that the 4th and the 8ht equations are consequences from the rest ones and after some transformations we have reached a system of 6 equations as there are unknown functions.We emphasize that classical Lorentz-Dirac radiation term and two- body equations of motion do not satisfy the basic relativistic equation
are derived on the basis of the original Dirac physical assumptions [4]. In [1] we have proved that the 4th and the 8ht equations are consequences from the rest ones and after some transformations we have reached a system of 6 equations as there are unknown functions.We emphasize that classical Lorentz-Dirac radiation term and two- body equations of motion do not satisfy the basic relativistic equation 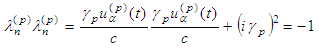 obviously fulfilled in our case [1].We also note that on the base of Wheeler-Feynman formalism [8], [9] the authors in [10]-[14] have been obtained interesting results. Our purpose, however, is to show the existence and uniqueness of a periodic solution of the two-body equations of motion obtained in [1]. We present the system in question in a suitable operator form and the fixed point of this operator appears a periodic solution of the system.Section 1 is an introduction and we rearrange equations of motion in more convenient form. Main results are given in Section 2. In Subsection 2.1 we derive radiation terms in an explicit form and show that they are bounded, that is, free of singularities. In Subsection 2.2 we formulate the main periodic problem and prove some preliminary assertions. In order to apply fixed point theorems from [5] we introduce suitable function spaces and operator whose fixed points are solutions of the periodic problem mentioned and give some lemmas. Supplement 1 contains preliminary estimates that imply the operator maps the solution set into itself. In Supplement 2 Lipschitz estimates of the operator and its derivatives are obtained. Subsection 2.3 contains the main result: two-body system has a unique periodic solution. Subsection 2.4 includes numerical test results. Section 3 is a conclusion and shows the adequacy of the main theorem.Recall denotations from [1]:
obviously fulfilled in our case [1].We also note that on the base of Wheeler-Feynman formalism [8], [9] the authors in [10]-[14] have been obtained interesting results. Our purpose, however, is to show the existence and uniqueness of a periodic solution of the two-body equations of motion obtained in [1]. We present the system in question in a suitable operator form and the fixed point of this operator appears a periodic solution of the system.Section 1 is an introduction and we rearrange equations of motion in more convenient form. Main results are given in Section 2. In Subsection 2.1 we derive radiation terms in an explicit form and show that they are bounded, that is, free of singularities. In Subsection 2.2 we formulate the main periodic problem and prove some preliminary assertions. In order to apply fixed point theorems from [5] we introduce suitable function spaces and operator whose fixed points are solutions of the periodic problem mentioned and give some lemmas. Supplement 1 contains preliminary estimates that imply the operator maps the solution set into itself. In Supplement 2 Lipschitz estimates of the operator and its derivatives are obtained. Subsection 2.3 contains the main result: two-body system has a unique periodic solution. Subsection 2.4 includes numerical test results. Section 3 is a conclusion and shows the adequacy of the main theorem.Recall denotations from [1]: 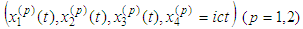 are the space - time coordinates of the moving particles;
are the space - time coordinates of the moving particles; 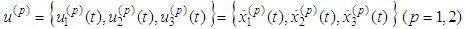
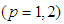 - velocities of the moving particles;
- velocities of the moving particles; 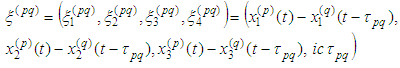
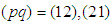 ;
; 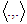 - dot product in 3-dimensional Euclidian space.In [1] we have derived the following equations of motion
- dot product in 3-dimensional Euclidian space.In [1] we have derived the following equations of motion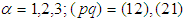 :
: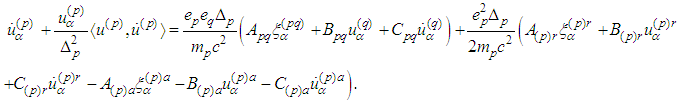 where
where
 Substituting
Substituting 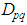
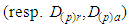 and
and 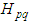
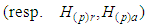 into
into 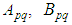
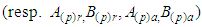 , transforming the expressions obtained under Dirac assumption
, transforming the expressions obtained under Dirac assumption 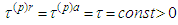 (cf. [4]) we have:
(cf. [4]) we have: 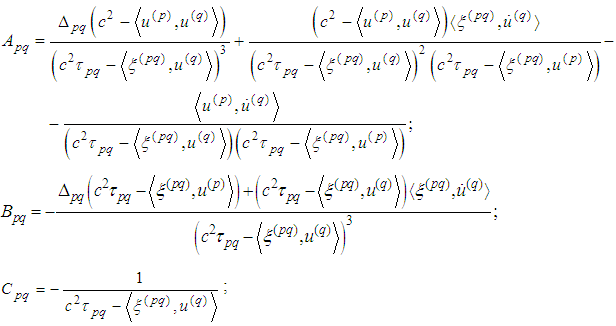
 Denoting by
Denoting by 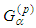 the right-hand sides of the above system we obtain
the right-hand sides of the above system we obtain 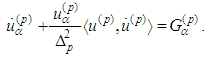 Solving with respect to
Solving with respect to 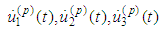 under assumption
under assumption 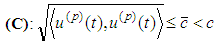 we reach the neutral system of six equations
we reach the neutral system of six equations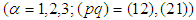 :
: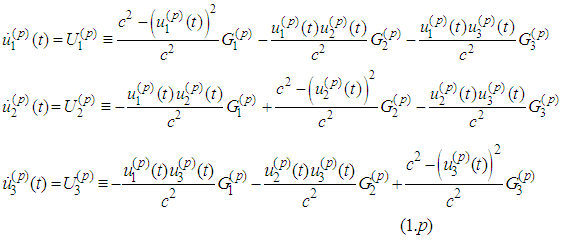 for six unknown functions
for six unknown functions 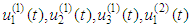
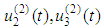 , where
, where 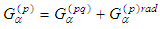 The summands
The summands 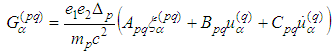 are called Lorentz terms, while the summand
are called Lorentz terms, while the summand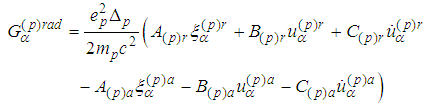 - radiation terms.
- radiation terms.2. Main Results
2.1. Explicit Form of the Radiation Term
- In what follows we derive the explicit form of the radiation terms. By
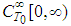 we denote the set of all infinitely differentiable
we denote the set of all infinitely differentiable 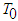 -periodic functions. We introduce the space of functions:
-periodic functions. We introduce the space of functions: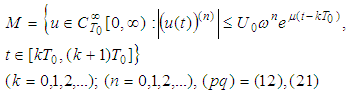 | (2.1) |
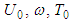 are positive constants and following A. Sommerfeld [7]
are positive constants and following A. Sommerfeld [7] 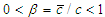 .Recall that
.Recall that 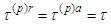 is assumed to be infinitely small parameter because
is assumed to be infinitely small parameter because 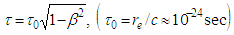 (cf. [2]). In fact
(cf. [2]). In fact 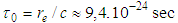 .Since we work in spaces of infinitely smooth functions, using the Taylor expansions we obtain
.Since we work in spaces of infinitely smooth functions, using the Taylor expansions we obtain 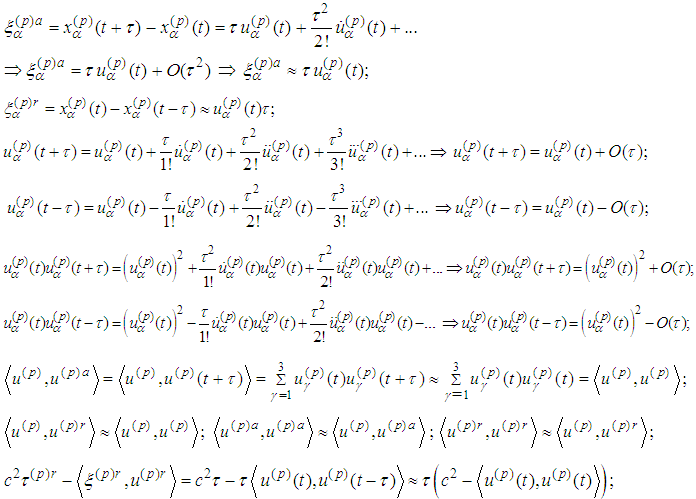
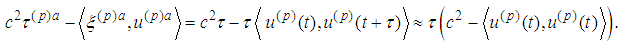 Then
Then
 In explicit form the radiation term is:
In explicit form the radiation term is: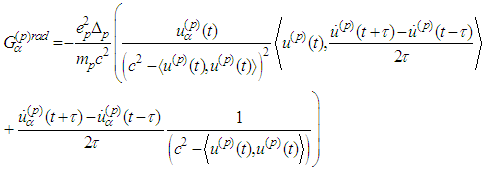
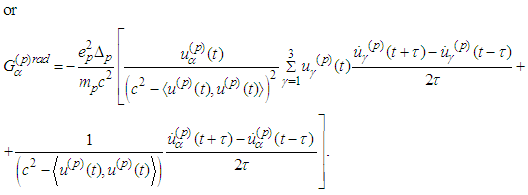 Lemma 2.1 The radiation term obtained is bounded provided
Lemma 2.1 The radiation term obtained is bounded provided 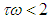 .Proof: We need an estimate of H. A. Schwartz difference quotient. In view of
.Proof: We need an estimate of H. A. Schwartz difference quotient. In view of 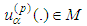 we obtain
we obtain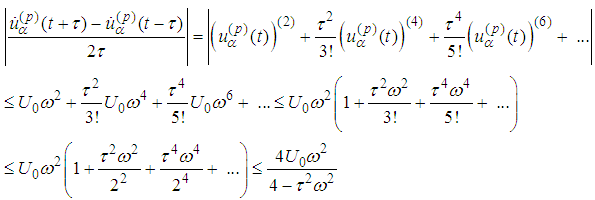
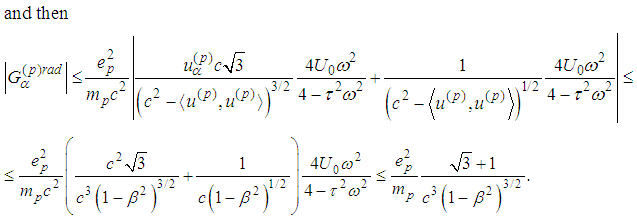 Lemma 2.1 is thus proved.
Lemma 2.1 is thus proved.2.2. Preliminary Assertions, Formulation of Main Periodic Problem and Lemmas
- Our main purpose is to obtain an existence-uniqueness of
 -periodic solution of the equations of motion (1.p). We consider (1.p) jointly with functional equations
-periodic solution of the equations of motion (1.p). We consider (1.p) jointly with functional equations 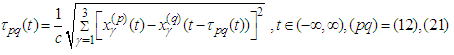 | (2.2) |
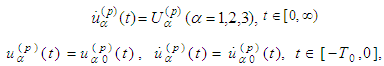 | (2.3) |
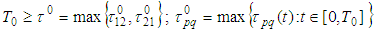 .Otherwise we take the initial interval
.Otherwise we take the initial interval 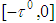 .We have however already proved in [15], [16] that (2.2) has a unique continuous solution for every Lipschitz continuous trajectories. That is why we can consider only (2.3).Remark 2.1 Here instead of inequality
.We have however already proved in [15], [16] that (2.2) has a unique continuous solution for every Lipschitz continuous trajectories. That is why we can consider only (2.3).Remark 2.1 Here instead of inequality 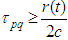 from [15], [16] we can use
from [15], [16] we can use 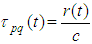 . It follows immediately from
. It follows immediately from 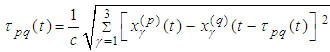 .Indeed, considering J. Kepler problem we put
.Indeed, considering J. Kepler problem we put 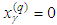 which implies the relation required. We prove some additional properties of
which implies the relation required. We prove some additional properties of 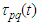 .Lemma 2.2 If
.Lemma 2.2 If 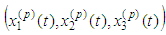 are smooth
are smooth 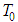 - periodic trajectories with velocities
- periodic trajectories with velocities 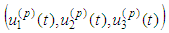 satisfying
satisfying 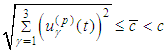 , then:1) (3.1) has a unique smooth
, then:1) (3.1) has a unique smooth 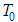 -periodic solution. 2) The derivative
-periodic solution. 2) The derivative 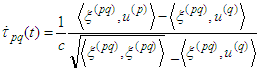 satisfies inequalities
satisfies inequalities 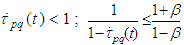 .Proof: 1. The proof can be accomplished as in [15], [16].2. Differentiating
.Proof: 1. The proof can be accomplished as in [15], [16].2. Differentiating 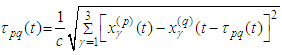 and solving with respect to
and solving with respect to 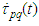 we obtain
we obtain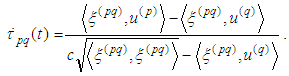 Using that (2.2) has a unique solution we have
Using that (2.2) has a unique solution we have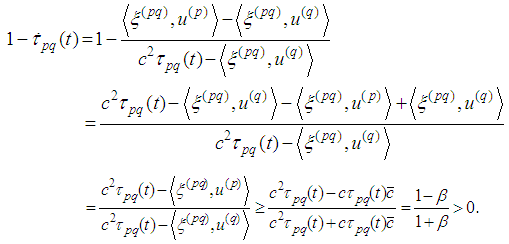 Obviously
Obviously 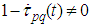 and besides
and besides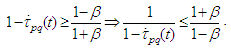 Lemma 2.2 is thus proved. The main difficulty is to define a suitable operator whose fixed points are solutions sought. Assuming that the initial point is
Lemma 2.2 is thus proved. The main difficulty is to define a suitable operator whose fixed points are solutions sought. Assuming that the initial point is 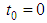 we introduce the function set:
we introduce the function set: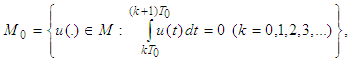 | (2.4) |
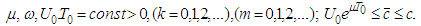 Introduce a family of pseudo-metrics
Introduce a family of pseudo-metrics 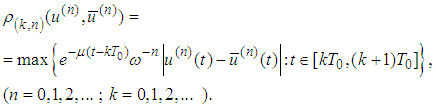 | (2.5) |
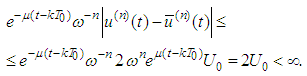 Therefore
Therefore 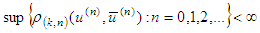 and we put
and we put 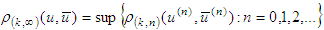 .Further on we put
.Further on we put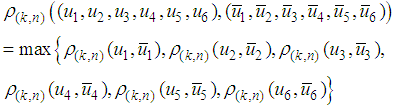 and
and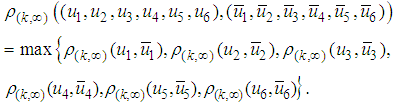 In fact
In fact 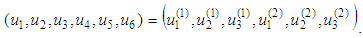 Assuming
Assuming 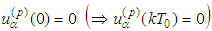 introduce the operator B as a 6-tuple
introduce the operator B as a 6-tuple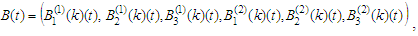 where
where | (2.6) |
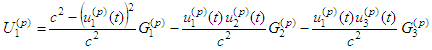
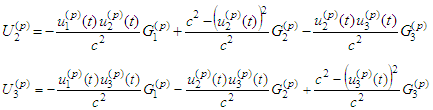 (p = 1, 2) we substitute the functions with retarded arguments
(p = 1, 2) we substitute the functions with retarded arguments 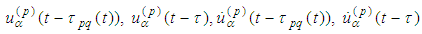 by the initial functions
by the initial functions 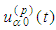 translated to the right on the interval
translated to the right on the interval 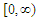 . By necessity we assume that
. By necessity we assume that 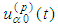 are such that their translated image on
are such that their translated image on 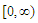 belong to
belong to 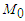 .We recall some assertions from [17]:Lemma 2.3 [17] If
.We recall some assertions from [17]:Lemma 2.3 [17] If 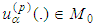 then
then 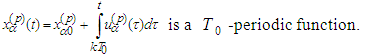 Lemma 2.4 [17] If the translated function
Lemma 2.4 [17] If the translated function 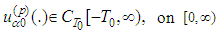 satisfies
satisfies 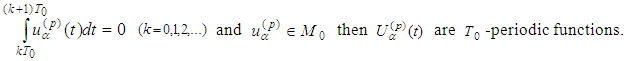 Lemma 2.5 [17] For every
Lemma 2.5 [17] For every 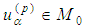 it follows
it follows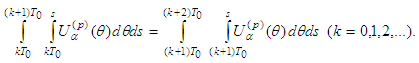 Lemma 2.6 [17] The function
Lemma 2.6 [17] The function 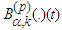 belongs to
belongs to 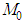 .Lemma 2.7 The following inequalities are fulfilled:
.Lemma 2.7 The following inequalities are fulfilled: 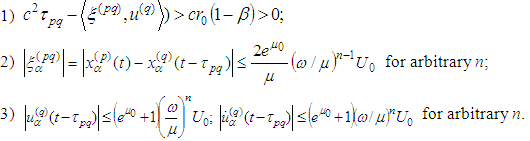 Proof:
Proof: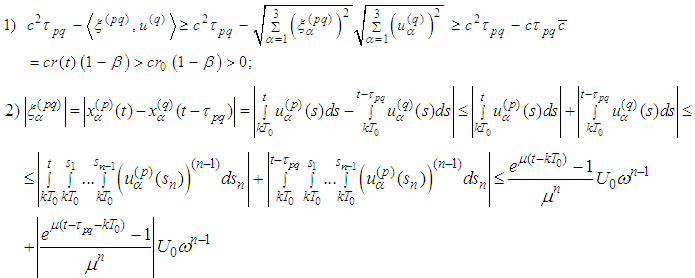
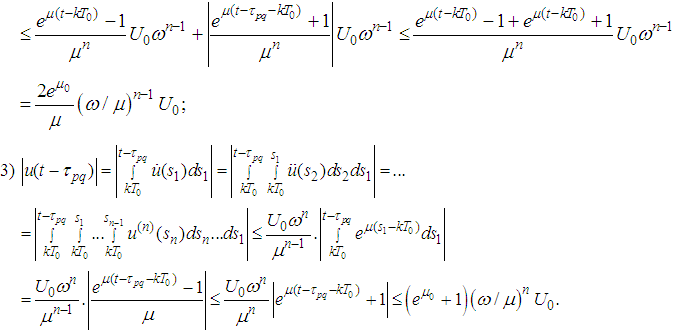 Lemma 2.7 is thus proved.Lemma 2.8 The following inequalities are fulfilled:
Lemma 2.7 is thus proved.Lemma 2.8 The following inequalities are fulfilled: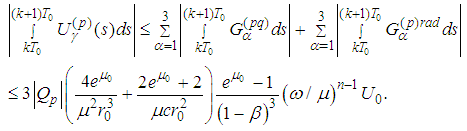 Proof: We use the inequality
Proof: We use the inequality 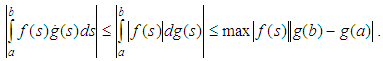 In the first summand of
In the first summand of 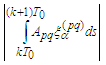 we use the estimate
we use the estimate 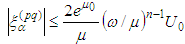 , while in the second and third ones
, while in the second and third ones 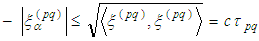 :
: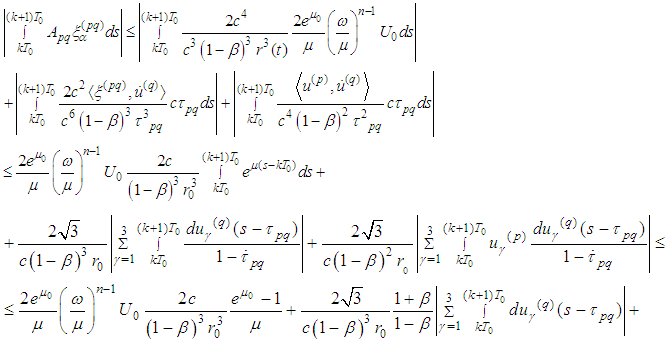
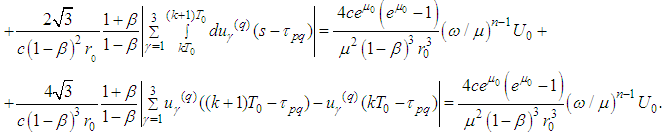 In
In 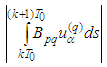 we estimate the first summand via
we estimate the first summand via 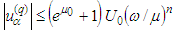 , while in the second one
, while in the second one 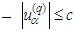 :
: 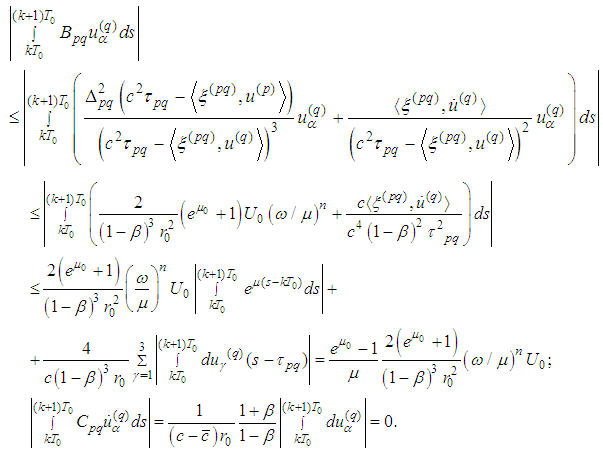 Therefore
Therefore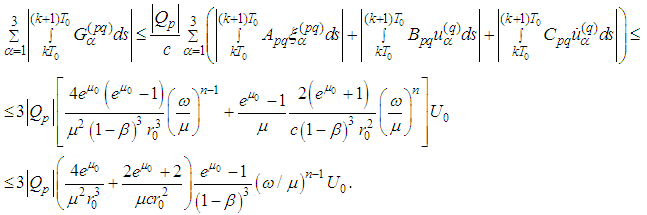 For the radiation part we obtain
For the radiation part we obtain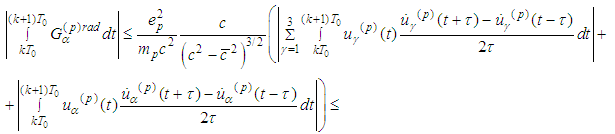
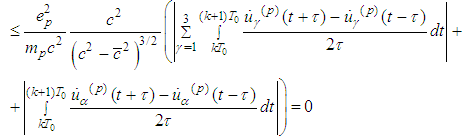 Lemma 2.8 is thus proved.Lemma 2.9 (Main Lemma) The periodic problem (2.3) has a unique solution
Lemma 2.8 is thus proved.Lemma 2.9 (Main Lemma) The periodic problem (2.3) has a unique solution 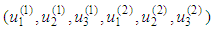 iff the operator B has a fixed point, belonging to
iff the operator B has a fixed point, belonging to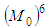 .Proof: Let
.Proof: Let 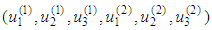 be a
be a 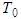 - periodic solution of (2.3). Then after integration in view of
- periodic solution of (2.3). Then after integration in view of 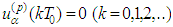 we obtain
we obtain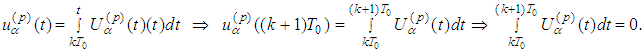 Therefore operator
Therefore operator 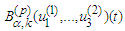 becomes
becomes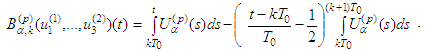 We have supposed that the system has a periodic solution. Then changing the order of integration we obtain
We have supposed that the system has a periodic solution. Then changing the order of integration we obtain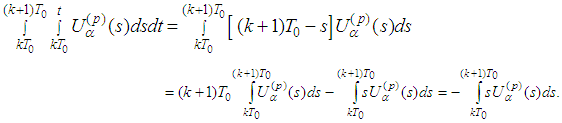 But
But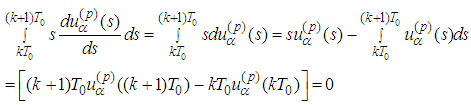 Therefore the following equality is satisfied
Therefore the following equality is satisfied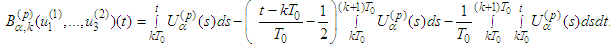 Conversely, let B has a fixed point
Conversely, let B has a fixed point 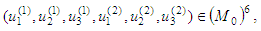 that is,
that is, 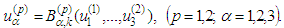 Therefore
Therefore 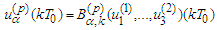 or
or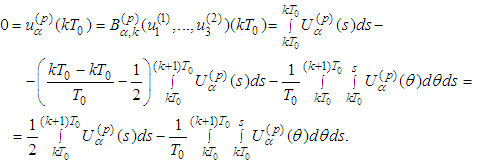 It follows
It follows 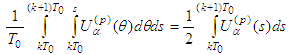 .We show that
.We show that 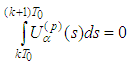 . Indeed, if
. Indeed, if 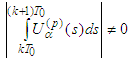 for sufficiently large
for sufficiently large 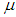 the inequality of Lemma 2.8 might be violated.Therefore the operator
the inequality of Lemma 2.8 might be violated.Therefore the operator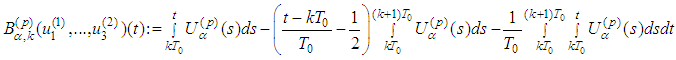 becomes
becomes 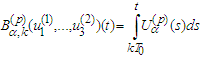 . Differentiating the last equalities we obtain that the fixed point of the operator is a periodic solution of (2.3).Lemma 2.9 is thus proved. Remark 2.2 We use the equality
. Differentiating the last equalities we obtain that the fixed point of the operator is a periodic solution of (2.3).Lemma 2.9 is thus proved. Remark 2.2 We use the equality 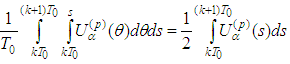 for further estimations.
for further estimations. 2.3. Existence-Uniqueness of a Periodic Solution of the Two-Body System
- Here we prove the main result:Theorem 2.1 (Main result) Let the following conditions be fulfilled:IN-1) the initial velocities
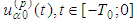 are
are 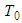 -periodic infinitely differentiable functions and initial trajectories are such that
-periodic infinitely differentiable functions and initial trajectories are such that 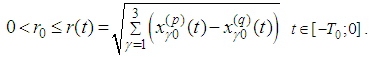 IN-2) the translations (to the right) of
IN-2) the translations (to the right) of 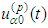 on
on 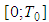 are restrictions of some functions from
are restrictions of some functions from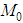 .Besides the following inequalities are satisfied:
.Besides the following inequalities are satisfied: 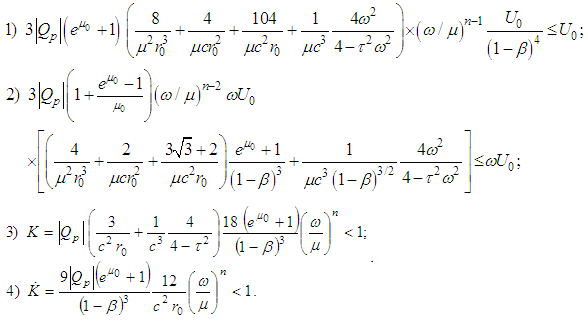 Then there exists a unique
Then there exists a unique 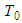 -periodic solution
-periodic solution 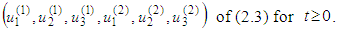 Proof: With accordance of the Main lemma 2.9 we have to prove that operator defined by (2.6) possesses a unique fixed point which means that (2.3) has a unique periodic solution.We use function spaces M and M0 defined by (2.1) and (2.4), respectively, and family of pseudo-metrics
Proof: With accordance of the Main lemma 2.9 we have to prove that operator defined by (2.6) possesses a unique fixed point which means that (2.3) has a unique periodic solution.We use function spaces M and M0 defined by (2.1) and (2.4), respectively, and family of pseudo-metrics 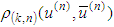 defined by (2.5).The set
defined by (2.5).The set 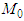 is endowed with a countable family of pseudo-metrics
is endowed with a countable family of pseudo-metrics 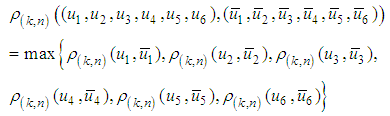 whose index set is
whose index set is 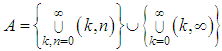 .The lemmas from Subsection 2.2 imply that the function
.The lemmas from Subsection 2.2 imply that the function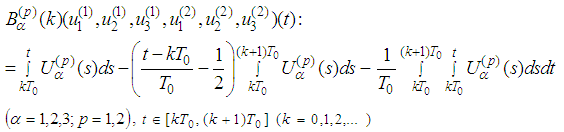 is
is 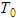 -periodic one.Estimates from Supplement 1.1 and condition 1) of the Main theorem imply
-periodic one.Estimates from Supplement 1.1 and condition 1) of the Main theorem imply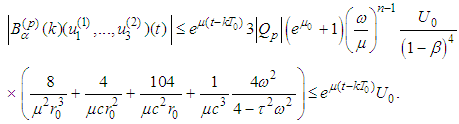 Estimates from Supplement 1.2 and condition 2) of the Main theorem imply
Estimates from Supplement 1.2 and condition 2) of the Main theorem imply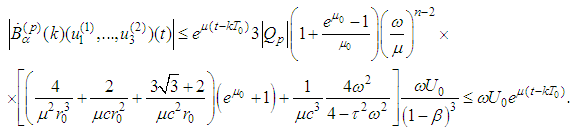 In a similar way we obtain for derivatives
In a similar way we obtain for derivatives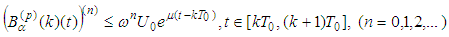 that is, the operator B maps the set
that is, the operator B maps the set 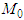 into itself.It remains to show that operator B is a contractive one. Indeed, in view of the inequalities obtained in Supplement 2 we have
into itself.It remains to show that operator B is a contractive one. Indeed, in view of the inequalities obtained in Supplement 2 we have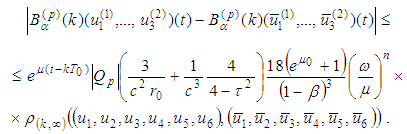 Multiplying by
Multiplying by 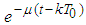 and taking the supremum in t we obtain
and taking the supremum in t we obtain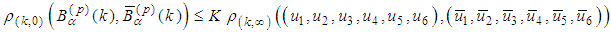 where
where 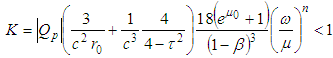 .For the derivatives we obtain
.For the derivatives we obtain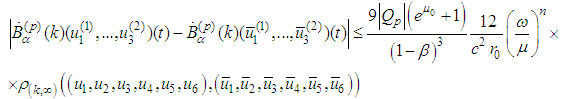 and therefore
and therefore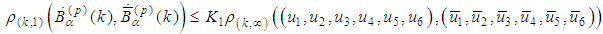 where
where 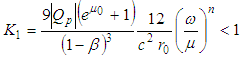 .Analogously we have
.Analogously we have 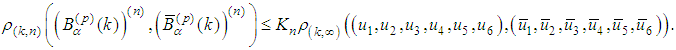 Taking the supremum in n we obtain
Taking the supremum in n we obtain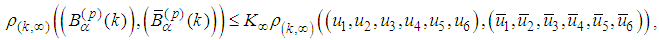 where
where 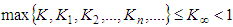 . This means B is a contractive operator in the sense of definition given in [5]. Its unique fixed point is a periodic solution of two-body system of equations.Theorem 2.1 is thus proved.
. This means B is a contractive operator in the sense of definition given in [5]. Its unique fixed point is a periodic solution of two-body system of equations.Theorem 2.1 is thus proved.2.4. Numerical Test Results
- Let us show that the inequalities of Theorem 2.1 are satisfied:
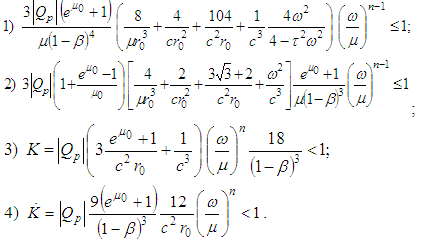 We recall that
We recall that 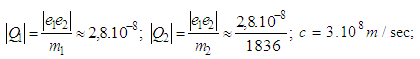
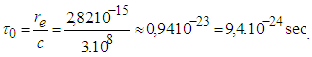 Since the radius of first Bohr orbit is
Since the radius of first Bohr orbit is 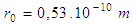 and its velocity is
and its velocity is 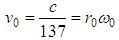 (1/137 is Sommerfeld fine structure constant), then
(1/137 is Sommerfeld fine structure constant), then 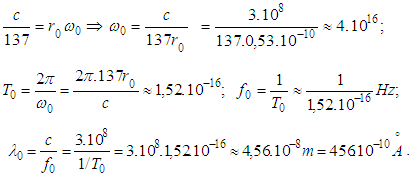 In the above inequalities n could be chosen arbitrarily large because the solution belongs to the space of infinitely differentiable functions. Our estimates require
In the above inequalities n could be chosen arbitrarily large because the solution belongs to the space of infinitely differentiable functions. Our estimates require 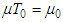 to be a constant. Here
to be a constant. Here 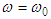 and we have to take
and we have to take 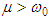 , for instance
, for instance 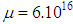 . Then
. Then 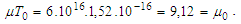 Therefore
Therefore 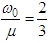 and
and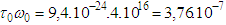 , that is condition
, that is condition 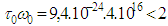 is satisfied. We choose
is satisfied. We choose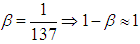 . For the inequalities we get
. For the inequalities we get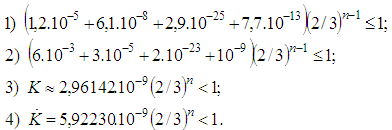 We notice that the initial conditions of Theorem 2.1 exclude the condition from [16] for escape trajectories.
We notice that the initial conditions of Theorem 2.1 exclude the condition from [16] for escape trajectories. 3. Conclusions
- It is easy to see that the inequalities are satisfied for every radius of “larger” orbit
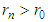 .Following [18] and [19] we would like to recall some difficulties of planetary model of the atom.Difficulty (1): It is known that the properties of an atom are determined by its electric field. The identity of their properties means that all of the hydrogen atoms possess identical electrical fields. In other words the electrons of all these atoms move in strictly identical orbits (for instance, circles or ellipses and so on). The shape of electron orbits must depend on the initial conditions of formation of the atom. It is clear that these initial conditions can be very different. Completely incomprehensible is why at various initial conditions the electron attaches the same orbit.Difficulty (2): In the planetary model of the hydrogen atom the electron moves in a stable orbit. This contradicts electrodynamics because the radiation of the electron leads to decreasing of its radius as a result it should be collided to the nucleus. This time is
.Following [18] and [19] we would like to recall some difficulties of planetary model of the atom.Difficulty (1): It is known that the properties of an atom are determined by its electric field. The identity of their properties means that all of the hydrogen atoms possess identical electrical fields. In other words the electrons of all these atoms move in strictly identical orbits (for instance, circles or ellipses and so on). The shape of electron orbits must depend on the initial conditions of formation of the atom. It is clear that these initial conditions can be very different. Completely incomprehensible is why at various initial conditions the electron attaches the same orbit.Difficulty (2): In the planetary model of the hydrogen atom the electron moves in a stable orbit. This contradicts electrodynamics because the radiation of the electron leads to decreasing of its radius as a result it should be collided to the nucleus. This time is 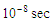 [18], [19].Our conclusion: It is not natural to expect that the applying of the methods of classical mechanics to relativistic objects will give adequate results. Namely:1) The orbits in question [18], [19] are obtained in the frame of classical mechanics, while we consider two-body problem in the relativistic case;2) We have found initial conditions (these are the conditions of our main Theorem 2.1) which guarantee an existence-uniqueness of a closed orbit; 3) We have considered equations with radiation terms and nevertheless there is unique periodic orbit for every stationary state without radiation. In other words the radiation is so small that it does not affect the stability of the atom. This fact is confirmed experimentally. In our model the hydrogen atom exists infinitely long. Finally, we would like to say that basic difficulties of the planetary model are overcome provided the considerations to be relativistic ones.Supplement 1. The Operator Maps Solution Set into Itself 1.1. Estimates of the Right-Hand Sides We have to show that the operator
[18], [19].Our conclusion: It is not natural to expect that the applying of the methods of classical mechanics to relativistic objects will give adequate results. Namely:1) The orbits in question [18], [19] are obtained in the frame of classical mechanics, while we consider two-body problem in the relativistic case;2) We have found initial conditions (these are the conditions of our main Theorem 2.1) which guarantee an existence-uniqueness of a closed orbit; 3) We have considered equations with radiation terms and nevertheless there is unique periodic orbit for every stationary state without radiation. In other words the radiation is so small that it does not affect the stability of the atom. This fact is confirmed experimentally. In our model the hydrogen atom exists infinitely long. Finally, we would like to say that basic difficulties of the planetary model are overcome provided the considerations to be relativistic ones.Supplement 1. The Operator Maps Solution Set into Itself 1.1. Estimates of the Right-Hand Sides We have to show that the operator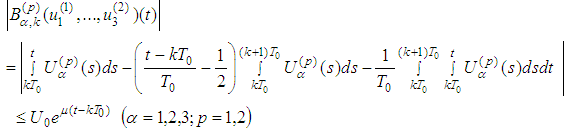 maps
maps 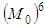 into itself.In view the previous Remark 5.2 we have:
into itself.In view the previous Remark 5.2 we have: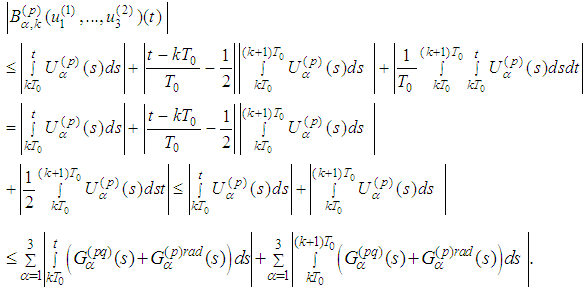 From the proof of the Main Lemma and the assertion of Lemma 2.8 we obtain
From the proof of the Main Lemma and the assertion of Lemma 2.8 we obtain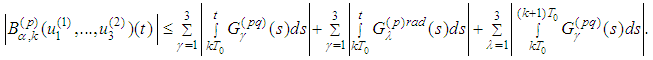 We have
We have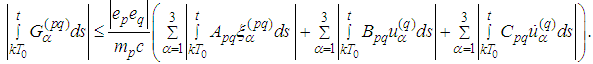 Having in mind Lemma 2.7 we use the estimate
Having in mind Lemma 2.7 we use the estimate 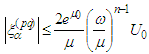 in the first summand of
in the first summand of 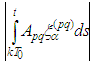 , while in the second and third ones ̶
, while in the second and third ones ̶ 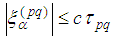 . Then in view of
. Then in view of 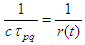 we have
we have In a similar way in the first summand of
In a similar way in the first summand of 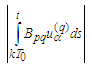 we use
we use 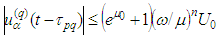 , while in the second one ̶
, while in the second one ̶ 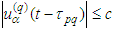 and get
and get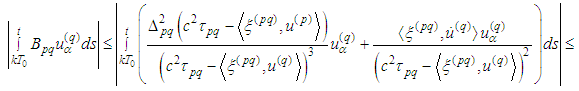
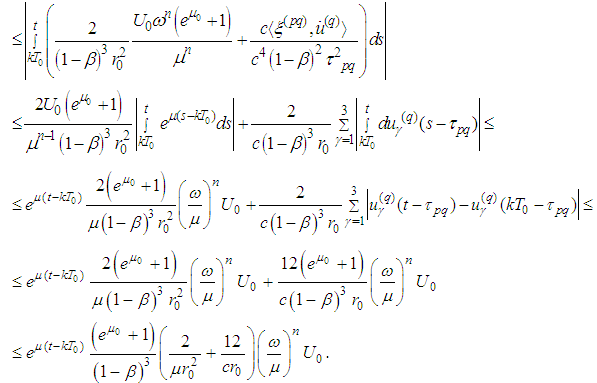 For
For 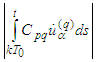 we have
we have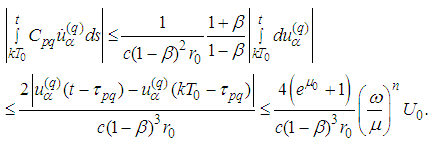 Then
Then 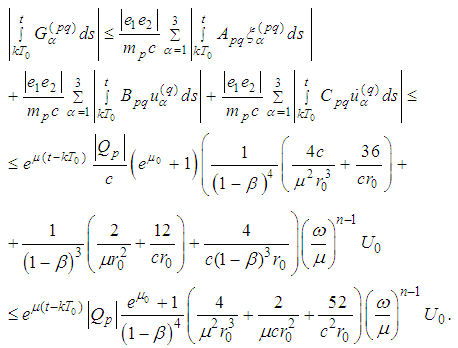 In a similar way we obtain
In a similar way we obtain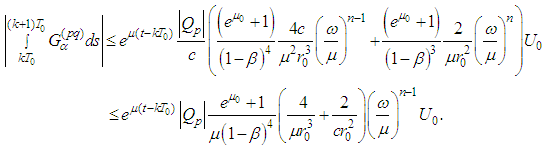 For the radiation term in view of
For the radiation term in view of 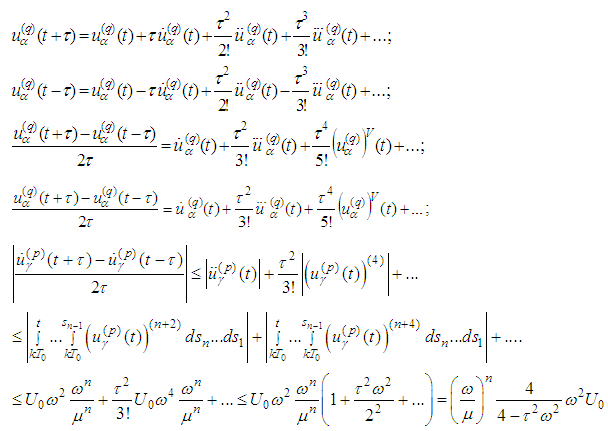 we obtain
we obtain Therefore the integral of the radiation term is bounded.We have already obtained that
Therefore the integral of the radiation term is bounded.We have already obtained that 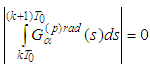 .Finally we obtain
.Finally we obtain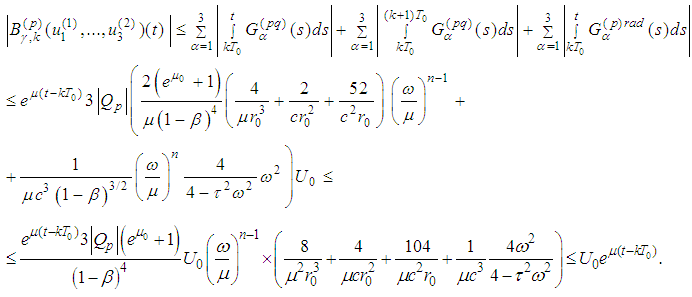 1.2. Estimates of the Derivatives For the derivative
1.2. Estimates of the Derivatives For the derivative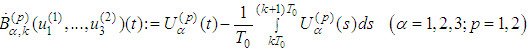 We use the above estimates and for
We use the above estimates and for 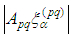 we obtain
we obtain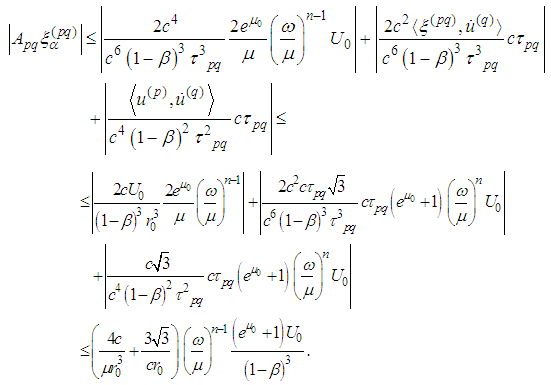 In a similar way in the first summand of
In a similar way in the first summand of 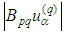 we use
we use 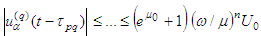 , while in the second one ̶̶
, while in the second one ̶̶ 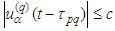 and have
and have 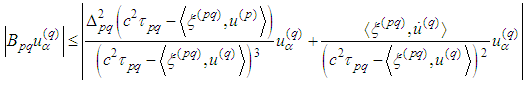
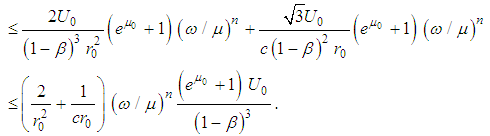 For
For 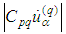 we have
we have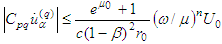 .Therefore
.Therefore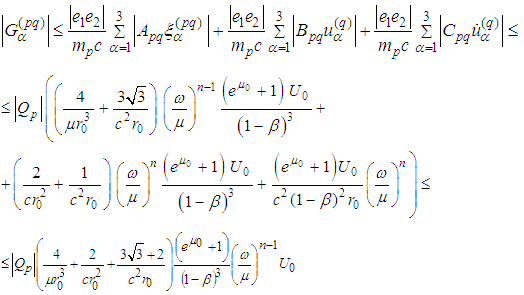 and
and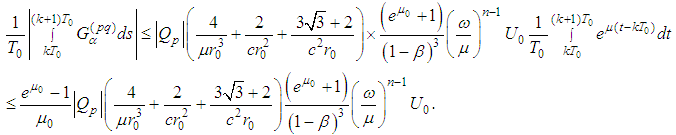 For the radiation term we can use the estimate from Lemma 2.1, namely
For the radiation term we can use the estimate from Lemma 2.1, namely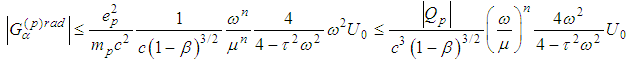 and then
and then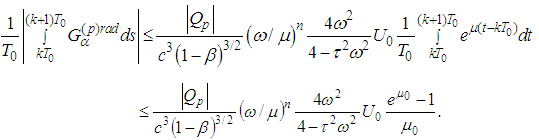 Therefore
Therefore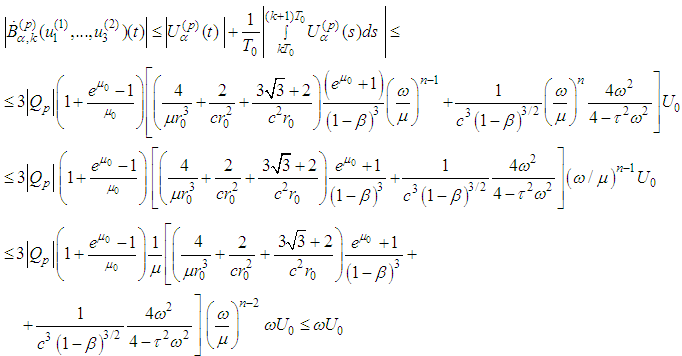 Supplement 2. Lipschitz Estimate2.1. Lipschitz Estimates of the Right-Hand Sides Prior to obtain Lipschitz estimates we notice
Supplement 2. Lipschitz Estimate2.1. Lipschitz Estimates of the Right-Hand Sides Prior to obtain Lipschitz estimates we notice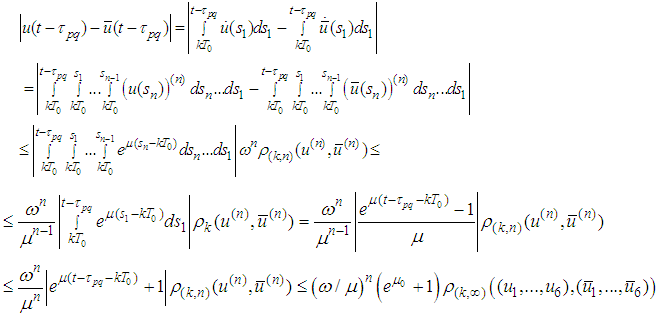 and for the derivatives we have the similar inequalities. Therefore we can obtain Lipschitz estimates only for derivatives
and for the derivatives we have the similar inequalities. Therefore we can obtain Lipschitz estimates only for derivatives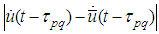 . They are
. They are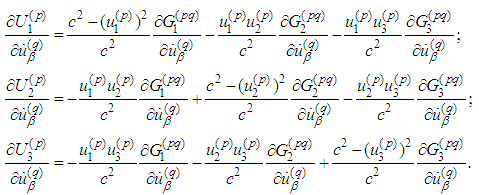 In order to simplify the next expressions we introduce the following denotation for H. A. Schwartz difference quotient:
In order to simplify the next expressions we introduce the following denotation for H. A. Schwartz difference quotient: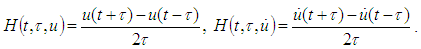 Then
Then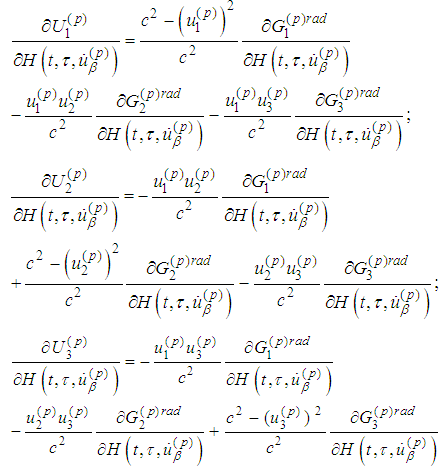 and in view of
and in view of 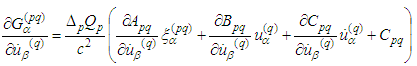
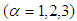 we have
we have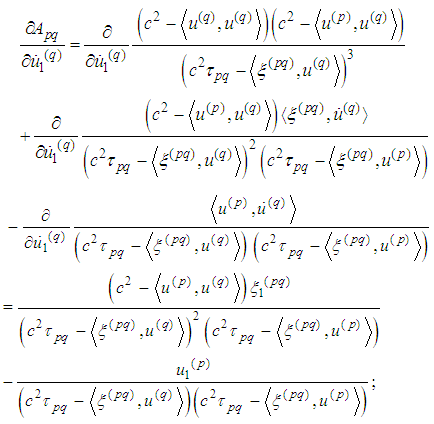
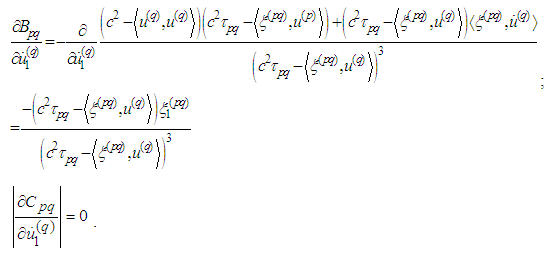 Then
Then 
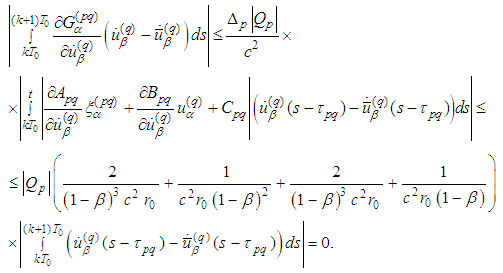 For the radiation term we obtain
For the radiation term we obtain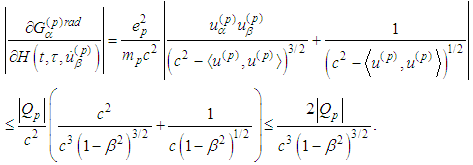 Since
Since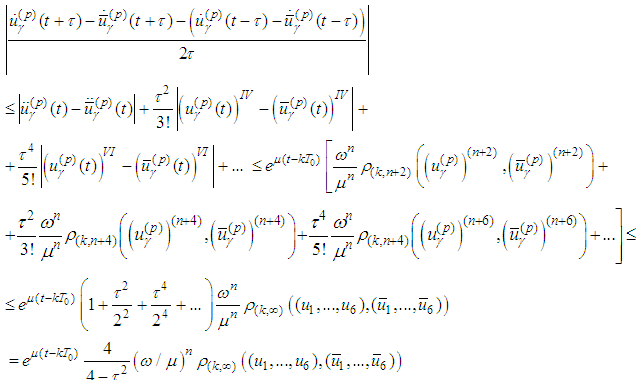 we have
we have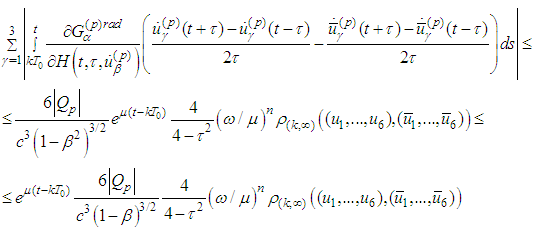 and
and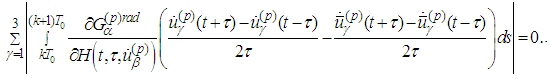 .Therefore the Lipschitz estimate for the operator is
.Therefore the Lipschitz estimate for the operator is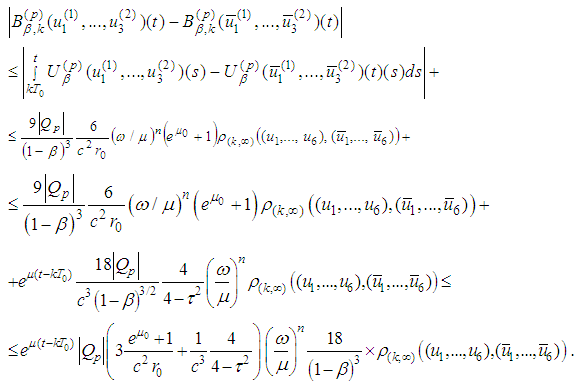 2.2. Lipschitz Estimates of the DerivativesIn view of
2.2. Lipschitz Estimates of the DerivativesIn view of 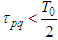 we obtain the following inequality:
we obtain the following inequality: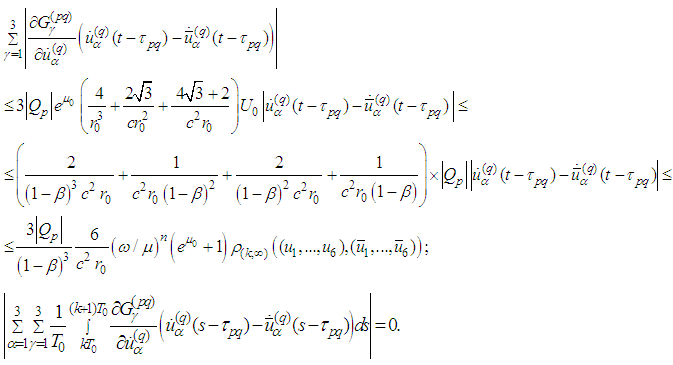 For the radiation term we have
For the radiation term we have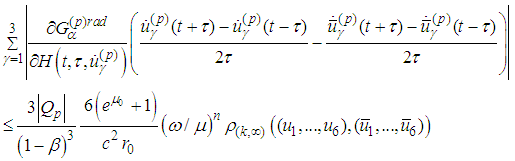 and
and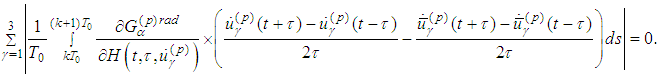 In view of
In view of 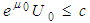 we have
we have
ACKNOWLEDGENTS
- 1) The author thanks Prof. D-r D.-A. Deckert for his kind invitation to deliver a lecture devoted to the problems of the present paper at the Seminar of International Junior Research Group "Interaction between Light and Matter”, Ludwig Maximilian University, Munich, June 2015.2) The author thanks the referee for his very useful remarks and suggestions which improved the paper.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML