Bratianu Daniel
Str. Teiului Nr. 16, Ploiesti, Romania
Correspondence to: Bratianu Daniel, Str. Teiului Nr. 16, Ploiesti, Romania.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
This paper tries to prove that the existence and properties of the electron’s spin can be established not only as a consequence of relativistic quantum mechanics, but also as a consequence of non-relativistic quantum mechanics of the Hydrogen atom or Hydrogenic atoms. It is, in fact, an extended model of the Hydrogen atom or Hydrogenic atoms. This new model starts from the assumption that to the foundation of atomic structure there is not only a potential of electrical nature, but also a potential of magnetic nature, which, together with the Coulomb potential, determine the movement of electrons around the atomic nucleus. As a consequence of this new model is obtained a non-relativistic theory of Hydrogen atom which takes into account the spin of the electron and leads us to a non-relativistic theory of the atom in agreement with the Stern-Gerlach experiment results. As well the model can be used in order to explain the spectrum of Alkali-atoms.
Keywords:
Spin, Magnetic field, Virtual, Nonrelativist, New model, Extended
Cite this paper: Bratianu Daniel, The Hydrogen Atom – Extended Model, International Journal of Theoretical and Mathematical Physics, Vol. 5 No. 6, 2015, pp. 151-159. doi: 10.5923/j.ijtmp.20150506.01.
1. Contents
Let us consider an electron that moves with velocity 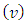 on a circular orbit in the meridian plane of a nucleus.Such an electron produces a "current loop" in this plane. From the fundamental laws of electromagnetism we know that any current loop produces a magnetic field perpendicular oriented to the plane of the orbit. The expression of the magnetic field at the center of such a "current loop" can be described, according to the laws of electromagnetism, by the formula:
on a circular orbit in the meridian plane of a nucleus.Such an electron produces a "current loop" in this plane. From the fundamental laws of electromagnetism we know that any current loop produces a magnetic field perpendicular oriented to the plane of the orbit. The expression of the magnetic field at the center of such a "current loop" can be described, according to the laws of electromagnetism, by the formula: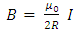 | (1) |
where 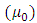 is the vacuum magnetic permeability,
is the vacuum magnetic permeability, 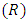 is the radius of the current loop, and
is the radius of the current loop, and 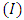 is the circulating current . Further, instead of using Cartesian coordinates
is the circulating current . Further, instead of using Cartesian coordinates 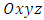 , it is convenient to introduce spherical coordinates
, it is convenient to introduce spherical coordinates 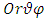 :
: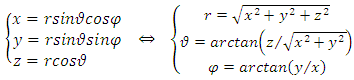 | (2) |
Therefore, we can assume that the component of the magnetic induction in the 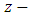 direction is
direction is  because
because 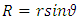 is the radius of the current loop in the meridian plane. But, from the electron’s point of view, the nucleus revolves around him. Thus, the nucleus produces also a “current loop”. Therefore we can assume that the expression of the magnetic induction
is the radius of the current loop in the meridian plane. But, from the electron’s point of view, the nucleus revolves around him. Thus, the nucleus produces also a “current loop”. Therefore we can assume that the expression of the magnetic induction 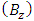 of the magnetic field produced by nucleus in the point where is placed the electron, has the form
of the magnetic field produced by nucleus in the point where is placed the electron, has the form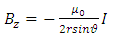 | (3) |
(the minus sign appears because the two systems, electron and atomic nucleus, have the opposite velocities, 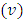 and
and 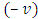 ). Now, as expression of circulating current
). Now, as expression of circulating current 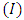 we can introduce the formula
we can introduce the formula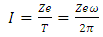 | (4) |
where 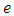 is the elementary charge,
is the elementary charge, 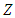 is the atomic number, and
is the atomic number, and 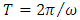 is the orbital period of the atomic nucleus. For the angular velocity of the nucleus
is the orbital period of the atomic nucleus. For the angular velocity of the nucleus 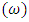 we allow the formula
we allow the formula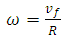 | (5) |
where 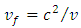 is the phase velocity of the de Broglie wave associated with the atomic nucleus. Thus, the expression of the circulating current
is the phase velocity of the de Broglie wave associated with the atomic nucleus. Thus, the expression of the circulating current 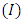 of the atomic nucleus becomes
of the atomic nucleus becomes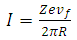 | (6) |
Substituting this expression in the expression of magnetic induction 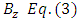 , we get
, we get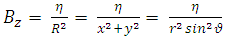 | (7) |
where the constant 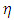 is given by
is given by 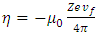 | (8) |
Further, we introduce the formula 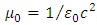 , where
, where 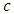 is the speed of light and
is the speed of light and 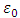 is the vacuum permittivity, so that the constant
is the vacuum permittivity, so that the constant 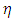 of
of 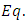 (8) can be rewritten as
(8) can be rewritten as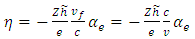 | (9) |
where 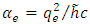 is the fine structure constant,
is the fine structure constant, 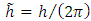 is the reduced Planck constant, and
is the reduced Planck constant, and 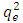 is the well-known expression
is the well-known expression 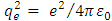 . Thus, we admit that from the electron’s point of view, the nucleus produces a magnetic field, whose expression can be written in vectorial form as
. Thus, we admit that from the electron’s point of view, the nucleus produces a magnetic field, whose expression can be written in vectorial form as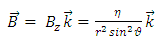 | (10) |
where 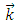 is the unit vector along
is the unit vector along 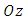 axis, and
axis, and 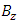 is the
is the 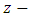 component of the magnetic induction
component of the magnetic induction 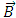 . Therefore, in order to correctly describe the motion of the electron, we must appeal to the Hamilton function of a particle with electric charge
. Therefore, in order to correctly describe the motion of the electron, we must appeal to the Hamilton function of a particle with electric charge 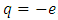 , located in an electromagnetic field represented in terms of the scalar and vector potentials
, located in an electromagnetic field represented in terms of the scalar and vector potentials 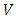 and
and 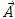 . So, we introduce the Hamiltonian operator of the form
. So, we introduce the Hamiltonian operator of the form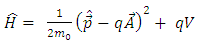 | (11) |
where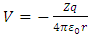 | (12) |
is the expression of the scalar potential 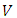 and
and 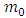 is the rest mass of the electron. We do not know the expression of the vector potential
is the rest mass of the electron. We do not know the expression of the vector potential 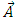 . But, we know that for an electron located into a constant magnetic field, we can write this expression as
. But, we know that for an electron located into a constant magnetic field, we can write this expression as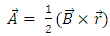 | (13) |
We keep this expression for the case when the magnetic induction (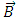 ) is a function of the position
) is a function of the position 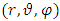 of the electron. Therefore, substituting
of the electron. Therefore, substituting 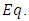 (10) into
(10) into 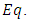 (13), the vector potential
(13), the vector potential 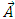 becomes
becomes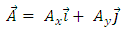 | (14) |
where 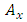 and
and 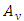 are
are 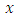 and
and 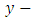 components of the potential vector
components of the potential vector 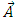
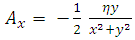 | (15) |
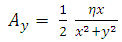 | (16) |
in Cartesian coordinates 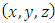 , and
, and 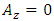 . Now, if we apply the transformations (2), we get
. Now, if we apply the transformations (2), we get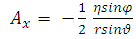 | (17) |
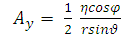 | (18) |
in spherical polar coordinates 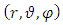 . Thus, the Hamiltonian operator
. Thus, the Hamiltonian operator 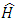 of the electron can be decomposed as the sum
of the electron can be decomposed as the sum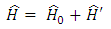 | (19) |
where the expressions of the operators 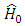 and
and 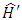 , according to
, according to 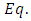 (11), are given by the formulas
(11), are given by the formulas 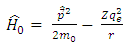 | (20) |
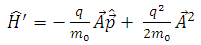 | (21) |
Now, with the aid of components 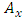 and
and 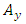 and of the transformations (2), we can find the expressions
and of the transformations (2), we can find the expressions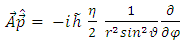 | (22) |
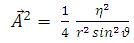 | (23) |
so that 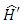 can be written as
can be written as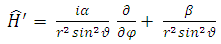 | (24) |
where the constants 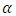 and
and 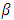 are given by the relations :
are given by the relations :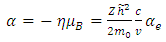 | (25) |
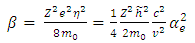 | (26) |
in which 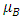 is the Bohr magneton
is the Bohr magneton 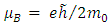 . Let us now consider the Schrodinger equation for an electron in the electromagnetic field of a nucleus of charge
. Let us now consider the Schrodinger equation for an electron in the electromagnetic field of a nucleus of charge 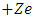
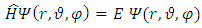 | (27) |
We assume a variables separable solution to this equation of the form 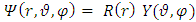 . Substituting this solution in
. Substituting this solution in 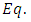 (27), after the separation of variables, we get the following two independent equations:
(27), after the separation of variables, we get the following two independent equations: 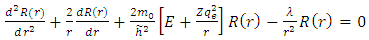 | (28) |
for radial wave function, and respectively 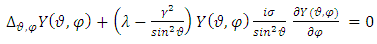 | (29) |
for the angular wave function, and the constants are given by the formulas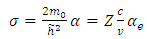 | (30) |
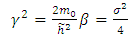 | (31) |
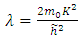 | (32) |
The constant 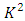 is the separation constant, and
is the separation constant, and 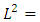
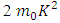 signifies the angular momentum squared. We assume again a variables separable solution to the second equation
signifies the angular momentum squared. We assume again a variables separable solution to the second equation 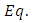 (29) of the form
(29) of the form 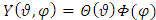 . Thus this equation can be separated in others two independent equations
. Thus this equation can be separated in others two independent equations 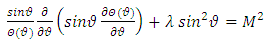 | (33) |
and respectively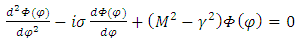 | (34) |
where the constant 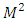 is the separation constant. After the change of variable
is the separation constant. After the change of variable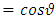 , the first equation
, the first equation 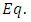 (33) can be rewritten as the well-known equation
(33) can be rewritten as the well-known equation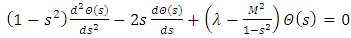 | (35) |
For the second equation 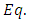 (34), we assume a solution of the form
(34), we assume a solution of the form 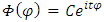 , where
, where 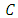 is a real constant. From the normalization condition we find the value of constant
is a real constant. From the normalization condition we find the value of constant 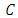 as
as 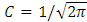 . Inserting the solution of
. Inserting the solution of 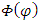 into Eq. (34), we obtain now the following characteristic equation
into Eq. (34), we obtain now the following characteristic equation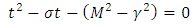 | (36) |
This is a quadratic equation for which, according to Eq. (31), we find the roots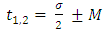 | (37) |
Now, we must consider the azimuth boundary condition 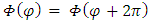 which imposes the conditions
which imposes the conditions 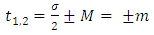 | (38) |
where 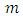 is a positive integer (including zero). Thus, we can write the constant
is a positive integer (including zero). Thus, we can write the constant 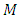 as
as 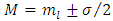 , where we have used the notation
, where we have used the notation 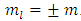 . Further, we introduce for the constant
. Further, we introduce for the constant 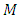 another notation
another notation 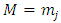 , so that we can write
, so that we can write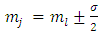 | (39) |
where 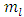 is the well-known orbital magnetic quantum number. Therefore, the solution
is the well-known orbital magnetic quantum number. Therefore, the solution 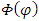 becomes
becomes 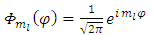 | (40) |
Turning now to 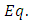 (35), we assume here a solution of the form
(35), we assume here a solution of the form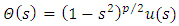 | (41) |
which replaced in this equation leads us to the following differential equation for unknown function 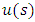
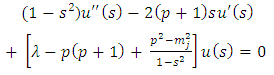 | (42) |
In order to exclude the singularities of the points 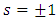 , we must impose the condition
, we must impose the condition 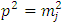 which generates the values of the exponent
which generates the values of the exponent 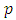 as
as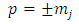 | (43) |
and the equation 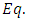 (42) gets the following well-known form
(42) gets the following well-known form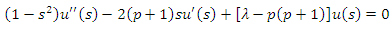 | (44) |
A solution may be found if we admit for 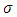 the value
the value 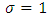 . With this value for
. With this value for 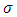 , the solution
, the solution 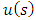 of Eq. (44) can be written as
of Eq. (44) can be written as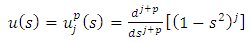 | (45) |
if we admit that the constant 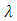 has the expression
has the expression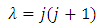 | (46) |
where 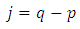 | (47) |
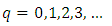 | (48) |
(the proof of formulas (46), (47) is provided by the Annex 1)Another solution for  may be also
may be also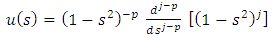 | (49) |
for the same 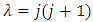 and
and 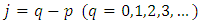 Indeed, if we substitute
Indeed, if we substitute 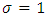 in Eq. (30) and Eq. (39), we find that the velocity of the electron
in Eq. (30) and Eq. (39), we find that the velocity of the electron 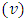 gets the expression
gets the expression 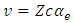 | (50) |
and the quantum number 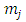 becomes
becomes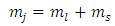 | (51) |
where 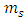 is the spin magnetic quantum number
is the spin magnetic quantum number 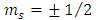 From Eq. (43) and Eq. (47), we can obtain now the formula
From Eq. (43) and Eq. (47), we can obtain now the formula 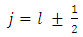 | (52) |
where 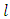 is the orbital quantum number, given by the formula
is the orbital quantum number, given by the formula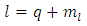 | (53) |
Also, from Eqs. (43) and (47), we can find the inequalities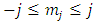 | (54) |
where 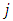 and
and 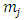 take only half-integers values (It should be mentioned here that in the state
take only half-integers values (It should be mentioned here that in the state 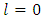 the quantum number
the quantum number 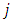 can have a single value,
can have a single value, 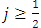 , so we can write
, so we can write 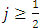 ). Substituting now the solution
). Substituting now the solution 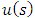 of Eq. (45) into Eq. (41), for
of Eq. (45) into Eq. (41), for 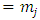 , we can write the solution
, we can write the solution 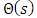 of Eq. (35) in the general form
of Eq. (35) in the general form 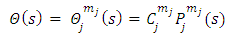 | (55) |
where the 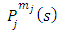 function is the solution Legendre's equation Eq. (35) for the half-integers quantum numbers
function is the solution Legendre's equation Eq. (35) for the half-integers quantum numbers 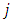 and
and 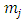
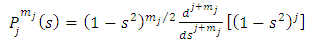 | (56) |
Because this solution must be finite on the interval 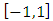 we must permit for
we must permit for 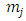 only the values
only the values 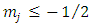 . The constants
. The constants 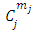 are the multiplication factors determined by the normalization condition which gives
are the multiplication factors determined by the normalization condition which gives 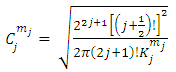 | (57) |
(the proof is provided by the Annex 2)The expression of the 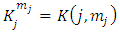 coefficients is given by the formula
coefficients is given by the formula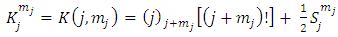 | (58) |
the coefficients 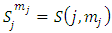 have the expression
have the expression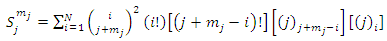 | (59) |
and the symbols 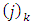 are given by the expressions
are given by the expressions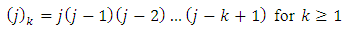 | (60) |
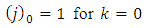 | (61) |
The 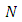 upper limit of the sum from Eq. (59) is
upper limit of the sum from Eq. (59) is 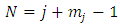 and the symbols
and the symbols 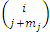 are combinations of
are combinations of 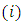 from a set of
from a set of 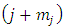 (the binomial coefficients).
(the binomial coefficients). 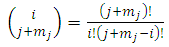 | (62) |
Now, it is convenient to define a radial coordinate with no units as 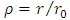 where
where 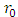 is the unit length or radius of the first Bohr orbit
is the unit length or radius of the first Bohr orbit 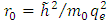 . Thus, we obtain the radial equation Eq. (28) for the Hydrogenic atom as
. Thus, we obtain the radial equation Eq. (28) for the Hydrogenic atom as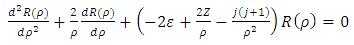 | (63) |
where ε is a dimensionless constant 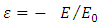 and
and 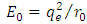 is known as the energy unit. We assumed now a solution of the form
is known as the energy unit. We assumed now a solution of the form 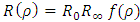 to this equation, where we have
to this equation, where we have 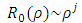 and
and 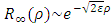 as asymptotic solutions of radial equation. Further, for generality, we can write
as asymptotic solutions of radial equation. Further, for generality, we can write 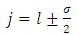 | (64) |
Substituting the solution 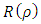 into radial equation Eq. (63), we find the equation for the unknown radial function
into radial equation Eq. (63), we find the equation for the unknown radial function 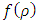
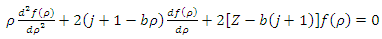 | (65) |
where we have introduced the notation 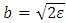 . We can simplify this equation if we introduce a new variable with no units
. We can simplify this equation if we introduce a new variable with no units 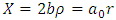 where
where 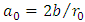 so that we can write our differential equation as
so that we can write our differential equation as 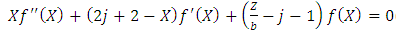 | (66) |
Now we can make the notations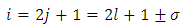 | (67) |
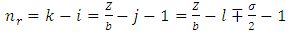 | (68) |
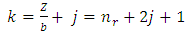 | (69) |
where the indexes 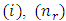 and
and 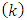 must be integers. So we can bring the equation to the following final form
must be integers. So we can bring the equation to the following final form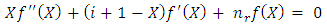 | (70) |
The solution of this equation is a polynomial of degree 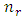
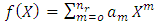 which leads us to following recursion relation between coefficients
which leads us to following recursion relation between coefficients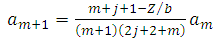 | (71) |
Because the maximum value of 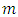 is the degree of the polynomial, we find the condition
is the degree of the polynomial, we find the condition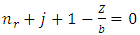 | (72) |
Therefore, the polynomial 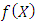 is the same well-known generalized (associated) Laguerre polynomial
is the same well-known generalized (associated) Laguerre polynomial 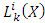 . So, the radial wave function
. So, the radial wave function 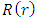 may be written as follows
may be written as follows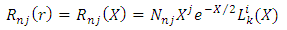 | (73) |
where 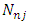 are the multiplication factors, whose expression can be determined by the normalization condition of the wave function
are the multiplication factors, whose expression can be determined by the normalization condition of the wave function 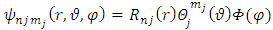 which leads us to the following equation
which leads us to the following equation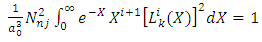 | (74) |
Using here the orthogonality condition of Laguerre polynomials written as 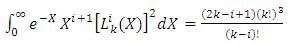 | (75) |
the normalization condition Eq. (74) takes the form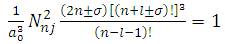 | (76) |
from which we deduce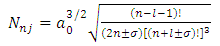 | (77) |
Substituting now Eq. (64) into Eqs. (72) and (70), taking into consideration the expression of principal quantum number 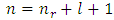 , we get the formulas
, we get the formulas 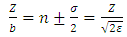 | (78) |
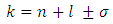 | (79) |
Therefore, we find that the total energy eigenvalues for the Hydrogenic atom are given by the expression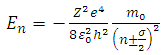 | (80) |
2. Conclusions
A first conclusion that can be drawn from this extended model of the hydrogenic atom is that the changes produced by the own magnetic field 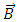 in the evolution of this type of atom are taken into account through the dimensionless variable
in the evolution of this type of atom are taken into account through the dimensionless variable 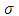 . From the above definitions of the indices
. From the above definitions of the indices 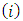 and
and 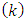 , in which this variable plays an important role, we deduce that it must be an integer. Also, we can observe that there is a relationship between the variable
, in which this variable plays an important role, we deduce that it must be an integer. Also, we can observe that there is a relationship between the variable 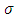 and velocity of the electron
and velocity of the electron 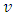 , according to the formula Eq. (30). From this formula we can deduce that the number
, according to the formula Eq. (30). From this formula we can deduce that the number 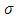 must be positive. Also, from the condition
must be positive. Also, from the condition 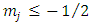 , we get
, we get 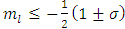 . As well, from Eq. (53), we can find the inequality
. As well, from Eq. (53), we can find the inequality 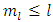 . Further, from these inequalities we get the condition
. Further, from these inequalities we get the condition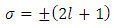 | (1) |
Therefore, we can consider that the 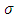 variable is an positive integer
variable is an positive integer 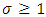 . So, we can observe that for
. So, we can observe that for 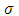 odd, although the electron spin stands out, the total energy formula does not correspond to the experimental results. This weakness of the model is certainly due to the fact that he does not take into account the radiative reaction force (the self force) which acts on the electron. Howbeit, if we admit that
odd, although the electron spin stands out, the total energy formula does not correspond to the experimental results. This weakness of the model is certainly due to the fact that he does not take into account the radiative reaction force (the self force) which acts on the electron. Howbeit, if we admit that 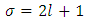 and we rewrite the radial equation Eq. (28) as follows
and we rewrite the radial equation Eq. (28) as follows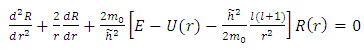 | (2) |
we can observe that it is possible to introduce here another expression for the potential energy 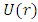 of the atom, as
of the atom, as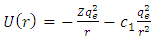 | (3) |
where 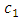 is a positive constant
is a positive constant 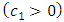 . Indeed, taking into consideration the expressions of the quantum numbers,
. Indeed, taking into consideration the expressions of the quantum numbers,  and
and  from Eqs. (46) and (64), we obtain the equation
from Eqs. (46) and (64), we obtain the equation 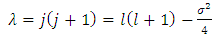 | (4) |
where we have chosen 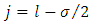 . Therefore, we can identify the second term of this equation as
. Therefore, we can identify the second term of this equation as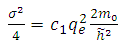 | (5) |
From this equation we can introduce the physics quantity 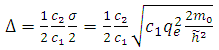 | (6) |
which is named the quantum defect, and for which the experimental formula can be given by the following expression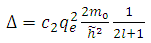 | (7) |
where 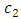 is a positive constant, too. These formulas are the experimental formulas of the alkali atoms. For these atoms the energy eigenvalues are in accordance with the expression Eq. (80), for
is a positive constant, too. These formulas are the experimental formulas of the alkali atoms. For these atoms the energy eigenvalues are in accordance with the expression Eq. (80), for 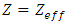 . Also, it can be shown that if we take
. Also, it can be shown that if we take 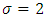 , and we introduce the formulas
, and we introduce the formulas 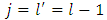 ,
, 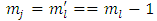 ,
, 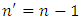 , can be obtained a theoretical situation in agreement with the results of the Stern-Gerlach experiment. The expression of the electron energy eigenvalues, for
, can be obtained a theoretical situation in agreement with the results of the Stern-Gerlach experiment. The expression of the electron energy eigenvalues, for 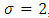 , can be written as
, can be written as 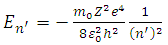 | (8) |
where 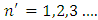 becomes principal quantum number.
becomes principal quantum number.
ANNEX 1
Let us consider the equation for  function
function 
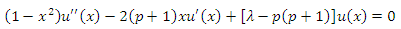 where
where 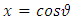 . We can look for the solution as a product between the function
. We can look for the solution as a product between the function 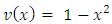 , raised to a power
, raised to a power 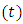 , and a power series in
, and a power series in 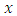
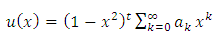 | (2) |
Substituting this solution into the initial equation Eq. (1), we get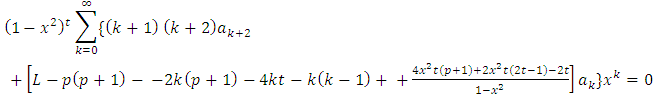 | (3) |
This equation has the singular points 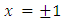 . In order to exclude them, we rewrite the numerator of the fraction as
. In order to exclude them, we rewrite the numerator of the fraction as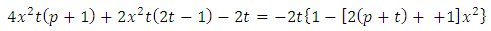 | (4) |
Now we can obtain a simplification of the fraction if we impose the condition 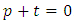 . Therefore, we get for the power
. Therefore, we get for the power 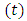 the values
the values 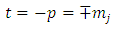 | (5) |
and the initial ecuation Eq. (1) becomes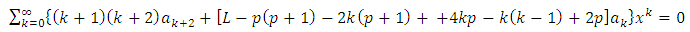 | (6) |
Now, after a rearrangement of terms, we rewrite this equation as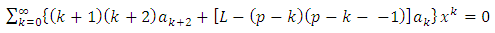 | (7) |
which leads us to the following recursion relation between the coefficients 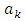
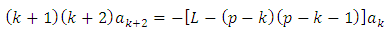 | (8) |
We impose now the condition as the series be reduced to a polynomial of maximum degree 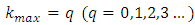 . Therefore, the recurrence relation Eq. (8) leads us to the formula
. Therefore, the recurrence relation Eq. (8) leads us to the formula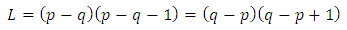 which can be written as
which can be written as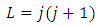 | (9) |
where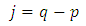 | (10) |
QED.
ANNEX 2
Starting from the solution of the Legendre equation for half-integers numbers 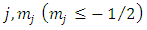
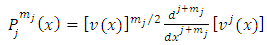 | (1) |
where the function 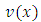 has the expression
has the expression 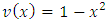 and is defined over the range
and is defined over the range 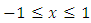 , we can show the orthogonality of
, we can show the orthogonality of 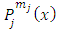 functions with the same superscript
functions with the same superscript 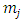 , but different subscripts
, but different subscripts 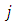 and
and 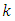
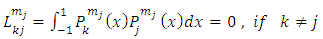 | (2) |
Also, we can calculate the expression for the coefficients of normalization 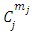 , when the indices
, when the indices 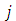 and
and 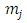 are half-integers numbers. Substituting the solutions Eq. (1) in the integral Eq. (3), we get
are half-integers numbers. Substituting the solutions Eq. (1) in the integral Eq. (3), we get 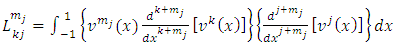 | (3) |
from which we can see that the indexes 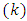 and
and 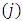 occur symmetrically and, therefore, without loss of generality, it is enough to investigate the case
occur symmetrically and, therefore, without loss of generality, it is enough to investigate the case 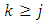 . We use now the formula of integration by parts
. We use now the formula of integration by parts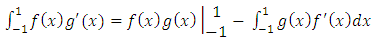 | (4) |
where, we note by 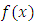 the first bracket, and by
the first bracket, and by 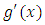 the two
the two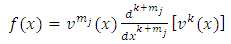 | (5) |
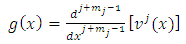 | (6) |
After the first integration, we obtain the following expression for 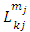
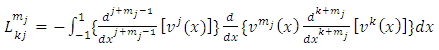 | (7) |
We continue the integration by parts, making the notations 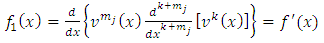 | (8) |
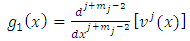 | (9) |
Applying again the formula of integration by parts Eq. (4), we obtain 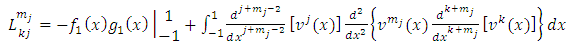 | (10) |
Taking the 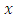 derivative of
derivative of 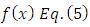 , we obtain
, we obtain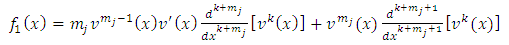 | (11) |
Now we can see that 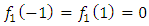 if
if 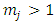 , so the integrated term will be zero, because it contains the
, so the integrated term will be zero, because it contains the 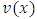 factor to a minimum power,
factor to a minimum power, 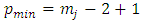 (where number 2 indicates the number of integrations), and the same
(where number 2 indicates the number of integrations), and the same 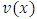 factor to a maximum power,
factor to a maximum power, 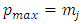 , and therefore, this factor will be zero at both endpoints
, and therefore, this factor will be zero at both endpoints 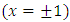 . Continuing the integration by parts, we can see that the degree of the derivative of the
. Continuing the integration by parts, we can see that the degree of the derivative of the 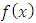 increases by 1 on each integration, while the degree of the derivative of the
increases by 1 on each integration, while the degree of the derivative of the 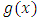 is reduced by 1 on each integration. After a number of
is reduced by 1 on each integration. After a number of 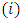 integrations by parts, the
integrations by parts, the 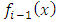 factor of the integrated term will be composed from a sum of terms which will include the
factor of the integrated term will be composed from a sum of terms which will include the 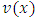 factor at the half-integers powers which extend from
factor at the half-integers powers which extend from 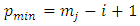 to
to 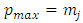 . All these terms will be zero at both endpoints, if
. All these terms will be zero at both endpoints, if 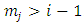 . So, after a number of
. So, after a number of 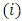 integrations by parts we can write the expression of
integrations by parts we can write the expression of 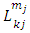 Eq. (7) as follows
Eq. (7) as follows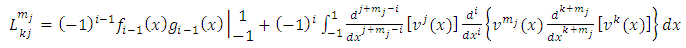 | (12) |
where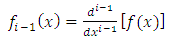 | (13) |
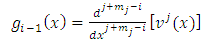 | (14) |
As we have seen above, for 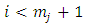 , the
, the 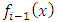 factor of integrated term will be zero. For
factor of integrated term will be zero. For 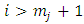 , this factor will no longer be zero. However, this time will be zero the second factor of product,
, this factor will no longer be zero. However, this time will be zero the second factor of product, 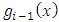 , because, after we calculate higher and higher derivatives, we will have a sum of terms containing the
, because, after we calculate higher and higher derivatives, we will have a sum of terms containing the 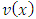 function as factor, and the lowest power of
function as factor, and the lowest power of 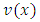 in any of these terms will be
in any of these terms will be 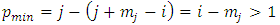 so that every term will go to zero at the endpoints. Therefore, if we integrate by parts
so that every term will go to zero at the endpoints. Therefore, if we integrate by parts 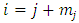 times, we get
times, we get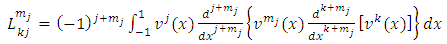 | (15) |
Now if we let 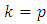 , since
, since 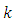 and
and 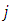 appeared symmetrically in the initial integral, we may write
appeared symmetrically in the initial integral, we may write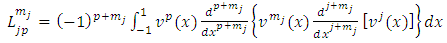 | (16) |
Also, we may consider the case 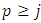 , which covers all possible cases. Further we can write the
, which covers all possible cases. Further we can write the 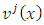 function as follows
function as follows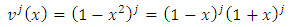 | (17) |
Using the higher derivative formula for the product (the Leibniz’s rule), we take the 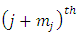 derivative of this function of the form
derivative of this function of the form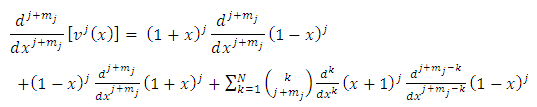 | (18) |
where 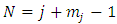 . Since each derivative of the function
. Since each derivative of the function 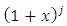 brings down the exponent and then reduces the exponent by 1, we may write
brings down the exponent and then reduces the exponent by 1, we may write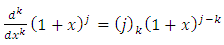 | (19) |
or correspondingly for the function 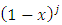 , we may also write
, we may also write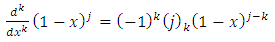 | (20) |
Now if we let 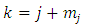 into Eqs. (21) and (22), we obtain
into Eqs. (21) and (22), we obtain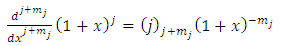 | (21) |
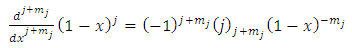 | (22) |
or, using the same symbol, we may also write 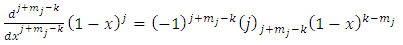 | (23) |
If we replace these formulas in Eq. (18) and then we multiply both sides of equation by the functions 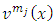 , we obtain
, we obtain 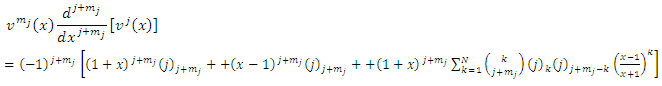 | (24) |
Now taking the 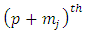 derivative of this expression, we get
derivative of this expression, we get 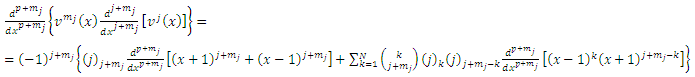 | (25) |
Since the indexes 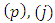 and
and 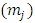 are half-integers numbers, the numbers
are half-integers numbers, the numbers 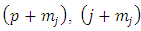 and
and 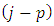 will be integers . Therefore, we can introduce the following higher derivatives formulas
will be integers . Therefore, we can introduce the following higher derivatives formulas 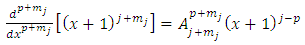 | (26) |
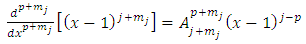 | (27) |
where the symbols 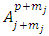 are the permutations of
are the permutations of 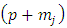 from a set of
from a set of 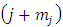
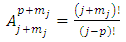 | (28) |
where we must impose the inequality 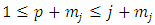 . Also, we can use now the inequality
. Also, we can use now the inequality 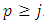 . Adding the
. Adding the 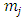 in the both members of this inequality, we get
in the both members of this inequality, we get 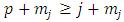 . From these inequalities we find the condition
. From these inequalities we find the condition 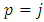 . Applying again the Leibniz's rule, further we may write
. Applying again the Leibniz's rule, further we may write 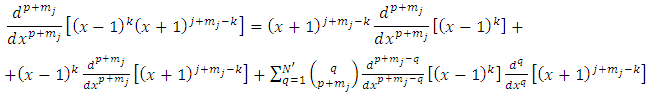 | (29) |
where 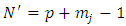 . Since
. Since 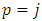 , the index
, the index 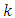 is an integer in the range
is an integer in the range 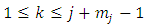 . Therefore, the first two terms of this equation will be zero. So, we can write
. Therefore, the first two terms of this equation will be zero. So, we can write 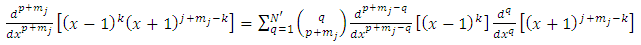 | (30) |
Now we use again the higher derivatives formulas as follows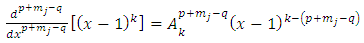 | (31) |
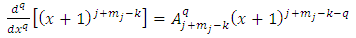 | (32) |
where we must impose the inequalities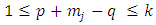 | (33) |
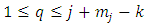 | (34) |
from which we deduce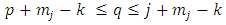 | (35) |
So, we have for the two indexes, 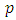 and
and 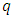 , the conditions
, the conditions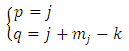 | (36) |
Inserting these conditions in Eqs. (31), (32) we get 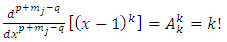 | (37) |
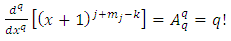 | (38) |
Also, we get 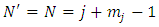 . Therefore, the expression Eq. (30) takes the final form
. Therefore, the expression Eq. (30) takes the final form 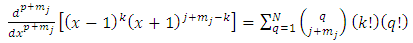 | (39) |
This is different from zero only when 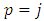 . For
. For 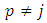 will be zero. Also, for
will be zero. Also, for 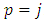 , Eqs. (26) and (27) becomes
, Eqs. (26) and (27) becomes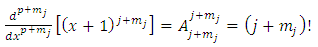 | (40) |
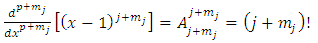 | (41) |
Thus, for 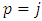 ,
, 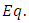 (25) can be written as
(25) can be written as 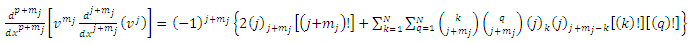 | (42) |
where, if we replace 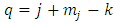 and we take into consideration the relations
and we take into consideration the relations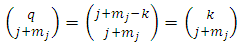 | (43) |
we can write this equation as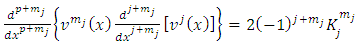 | (44) |
Therefore, the integral 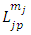 Eq. (16) takes the following form
Eq. (16) takes the following form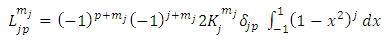 | (45) |
where, in agreement with the previous results, we have used here the Kronecker symbol 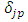 that shows the orthogonality of functions
that shows the orthogonality of functions 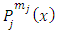 with
with 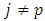 . Thus, for
. Thus, for 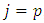 , the integral
, the integral 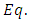 (45) becomes
(45) becomes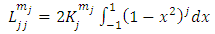 | (46) |
The final integral can be evaluated by using the trigonometric substitution 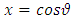 and the trigonometric formula
and the trigonometric formula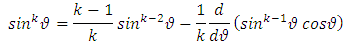 After an integration by parts, the integral can be written as
After an integration by parts, the integral can be written as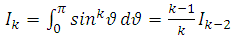 | (47) |
where 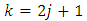 . Therefore, we can establish the following formula
. Therefore, we can establish the following formula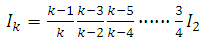 | (48) |
Since 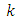 is an even number, we can write
is an even number, we can write 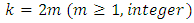 and the integral
and the integral 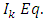 (48) becomes
(48) becomes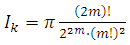 | (49) |
or, using the quantum number 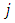 , the integral gets the formula
, the integral gets the formula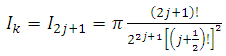 | (50) |
So, plugging this back into Eq. (46), we get finally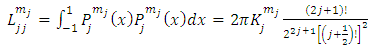 | (51) |
Now if we write the normalization condition for the functions 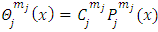 , we obtain
, we obtain 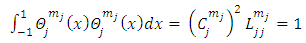 | (52) |
from which we deduce the constants 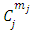 as follows
as follows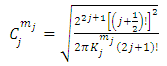 | (53) |
QED.
References
| [1] | www.physicspages.com/.../associated-legendre-. |
| [2] | www.physicspages.com/.../legendre-polynomial. |
| [3] | www.physicspages.com/.../hydrogen-atom-radial. |
| [4] | Physics.gmu.edu/…/hydrogen_atom |
| [5] | https://faculty.washington.edu/.../reading-26-27. |
| [6] | www.udel.edu/pchem/C444/.../04152008.pdf |
| [7] | TRAIAN CRETU FIZICA GENERALA VOL. 2 Ed. Tehnica BUCURESTI, 1984. |
| [8] | SPIRIDON DUMITRU MICROFIZICA Ed. DACIA, CLUJ-NAPOCA, 1984. |
| [9] | Prof. dr. doc. EMIL LUCA, Conf. dr. CORNELIU CIUBOTARIU, Conf. dr. GHEORGHE ZET, Conf. dr. ing. ANASTASIA PADURARU FIZICA GENERALA Editia a doua, Editura Didactica Si Pedagogica Bucuresti, 1981. |



 on a circular orbit in the meridian plane of a nucleus.Such an electron produces a "current loop" in this plane. From the fundamental laws of electromagnetism we know that any current loop produces a magnetic field perpendicular oriented to the plane of the orbit. The expression of the magnetic field at the center of such a "current loop" can be described, according to the laws of electromagnetism, by the formula:
on a circular orbit in the meridian plane of a nucleus.Such an electron produces a "current loop" in this plane. From the fundamental laws of electromagnetism we know that any current loop produces a magnetic field perpendicular oriented to the plane of the orbit. The expression of the magnetic field at the center of such a "current loop" can be described, according to the laws of electromagnetism, by the formula: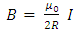
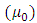 is the vacuum magnetic permeability,
is the vacuum magnetic permeability, 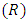 is the radius of the current loop, and
is the radius of the current loop, and 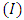 is the circulating current . Further, instead of using Cartesian coordinates
is the circulating current . Further, instead of using Cartesian coordinates 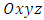 , it is convenient to introduce spherical coordinates
, it is convenient to introduce spherical coordinates 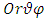 :
: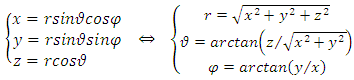
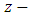 direction is
direction is  because
because 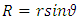 is the radius of the current loop in the meridian plane. But, from the electron’s point of view, the nucleus revolves around him. Thus, the nucleus produces also a “current loop”. Therefore we can assume that the expression of the magnetic induction
is the radius of the current loop in the meridian plane. But, from the electron’s point of view, the nucleus revolves around him. Thus, the nucleus produces also a “current loop”. Therefore we can assume that the expression of the magnetic induction 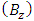 of the magnetic field produced by nucleus in the point where is placed the electron, has the form
of the magnetic field produced by nucleus in the point where is placed the electron, has the form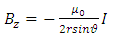
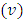 and
and 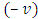 ). Now, as expression of circulating current
). Now, as expression of circulating current 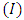 we can introduce the formula
we can introduce the formula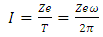
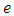 is the elementary charge,
is the elementary charge, 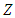 is the atomic number, and
is the atomic number, and 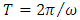 is the orbital period of the atomic nucleus. For the angular velocity of the nucleus
is the orbital period of the atomic nucleus. For the angular velocity of the nucleus 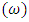 we allow the formula
we allow the formula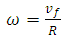
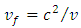 is the phase velocity of the de Broglie wave associated with the atomic nucleus. Thus, the expression of the circulating current
is the phase velocity of the de Broglie wave associated with the atomic nucleus. Thus, the expression of the circulating current 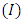 of the atomic nucleus becomes
of the atomic nucleus becomes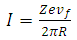
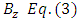 , we get
, we get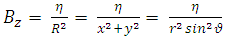
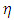 is given by
is given by 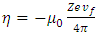
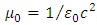 , where
, where 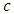 is the speed of light and
is the speed of light and 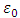 is the vacuum permittivity, so that the constant
is the vacuum permittivity, so that the constant 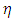 of
of 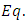 (8) can be rewritten as
(8) can be rewritten as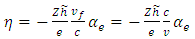
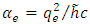 is the fine structure constant,
is the fine structure constant, 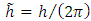 is the reduced Planck constant, and
is the reduced Planck constant, and 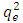 is the well-known expression
is the well-known expression 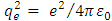 . Thus, we admit that from the electron’s point of view, the nucleus produces a magnetic field, whose expression can be written in vectorial form as
. Thus, we admit that from the electron’s point of view, the nucleus produces a magnetic field, whose expression can be written in vectorial form as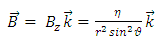
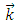 is the unit vector along
is the unit vector along 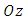 axis, and
axis, and 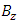 is the
is the 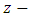 component of the magnetic induction
component of the magnetic induction 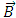 . Therefore, in order to correctly describe the motion of the electron, we must appeal to the Hamilton function of a particle with electric charge
. Therefore, in order to correctly describe the motion of the electron, we must appeal to the Hamilton function of a particle with electric charge 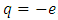 , located in an electromagnetic field represented in terms of the scalar and vector potentials
, located in an electromagnetic field represented in terms of the scalar and vector potentials 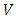 and
and 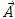 . So, we introduce the Hamiltonian operator of the form
. So, we introduce the Hamiltonian operator of the form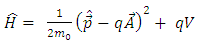
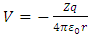
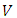 and
and 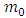 is the rest mass of the electron. We do not know the expression of the vector potential
is the rest mass of the electron. We do not know the expression of the vector potential 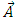 . But, we know that for an electron located into a constant magnetic field, we can write this expression as
. But, we know that for an electron located into a constant magnetic field, we can write this expression as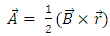
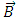 ) is a function of the position
) is a function of the position 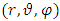 of the electron. Therefore, substituting
of the electron. Therefore, substituting 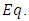 (10) into
(10) into 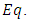 (13), the vector potential
(13), the vector potential 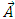 becomes
becomes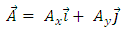
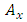 and
and 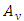 are
are 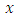 and
and 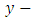 components of the potential vector
components of the potential vector 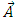
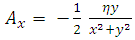
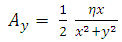
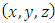 , and
, and 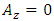 . Now, if we apply the transformations (2), we get
. Now, if we apply the transformations (2), we get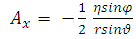
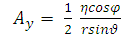
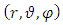 . Thus, the Hamiltonian operator
. Thus, the Hamiltonian operator 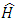 of the electron can be decomposed as the sum
of the electron can be decomposed as the sum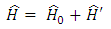
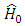 and
and 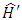 , according to
, according to 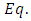 (11), are given by the formulas
(11), are given by the formulas 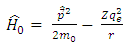
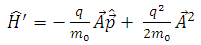
 and
and 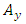 and of the transformations (2), we can find the expressions
and of the transformations (2), we can find the expressions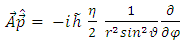
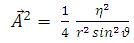
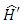 can be written as
can be written as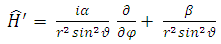
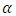 and
and 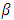 are given by the relations :
are given by the relations :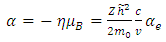
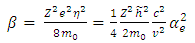
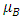 is the Bohr magneton
is the Bohr magneton 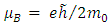 . Let us now consider the Schrodinger equation for an electron in the electromagnetic field of a nucleus of charge
. Let us now consider the Schrodinger equation for an electron in the electromagnetic field of a nucleus of charge 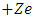
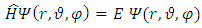
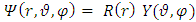 . Substituting this solution in
. Substituting this solution in 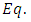 (27), after the separation of variables, we get the following two independent equations:
(27), after the separation of variables, we get the following two independent equations: 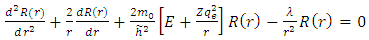
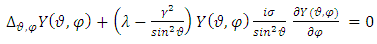
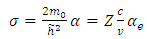
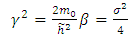
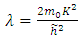
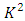 is the separation constant, and
is the separation constant, and 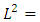
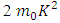 signifies the angular momentum squared. We assume again a variables separable solution to the second equation
signifies the angular momentum squared. We assume again a variables separable solution to the second equation 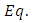 (29) of the form
(29) of the form 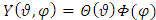 . Thus this equation can be separated in others two independent equations
. Thus this equation can be separated in others two independent equations 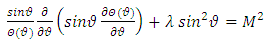
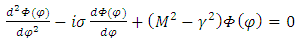
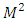 is the separation constant. After the change of variable
is the separation constant. After the change of variable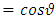 , the first equation
, the first equation 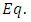 (33) can be rewritten as the well-known equation
(33) can be rewritten as the well-known equation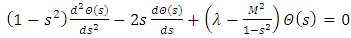
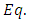 (34), we assume a solution of the form
(34), we assume a solution of the form 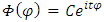 , where
, where 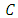 is a real constant. From the normalization condition we find the value of constant
is a real constant. From the normalization condition we find the value of constant 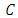 as
as 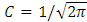 . Inserting the solution of
. Inserting the solution of 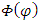 into Eq. (34), we obtain now the following characteristic equation
into Eq. (34), we obtain now the following characteristic equation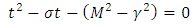
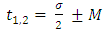
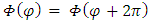 which imposes the conditions
which imposes the conditions 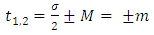
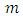 is a positive integer (including zero). Thus, we can write the constant
is a positive integer (including zero). Thus, we can write the constant 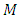 as
as 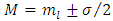 , where we have used the notation
, where we have used the notation 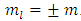 . Further, we introduce for the constant
. Further, we introduce for the constant 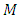 another notation
another notation 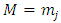 , so that we can write
, so that we can write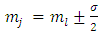
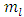 is the well-known orbital magnetic quantum number. Therefore, the solution
is the well-known orbital magnetic quantum number. Therefore, the solution 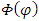 becomes
becomes 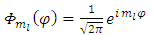
 (35), we assume here a solution of the form
(35), we assume here a solution of the form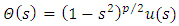
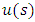
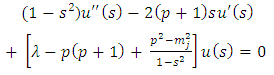
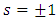 , we must impose the condition
, we must impose the condition 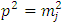 which generates the values of the exponent
which generates the values of the exponent 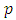 as
as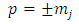
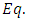 (42) gets the following well-known form
(42) gets the following well-known form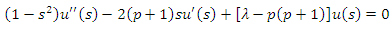
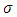 the value
the value 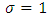 . With this value for
. With this value for 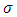 , the solution
, the solution 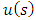 of Eq. (44) can be written as
of Eq. (44) can be written as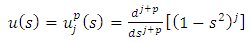
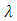 has the expression
has the expression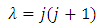
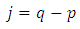
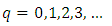
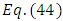 may be also
may be also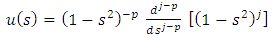
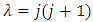 and
and 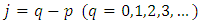 Indeed, if we substitute
Indeed, if we substitute 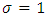 in Eq. (30) and Eq. (39), we find that the velocity of the electron
in Eq. (30) and Eq. (39), we find that the velocity of the electron 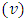 gets the expression
gets the expression 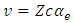
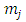 becomes
becomes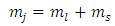
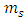 is the spin magnetic quantum number
is the spin magnetic quantum number 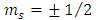 From Eq. (43) and Eq. (47), we can obtain now the formula
From Eq. (43) and Eq. (47), we can obtain now the formula 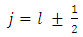
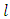 is the orbital quantum number, given by the formula
is the orbital quantum number, given by the formula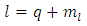
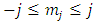
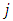 and
and 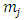 take only half-integers values (It should be mentioned here that in the state
take only half-integers values (It should be mentioned here that in the state 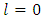 the quantum number
the quantum number 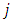 can have a single value,
can have a single value, 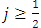 , so we can write
, so we can write 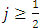 ). Substituting now the solution
). Substituting now the solution 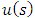 of Eq. (45) into Eq. (41), for
of Eq. (45) into Eq. (41), for 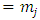 , we can write the solution
, we can write the solution 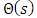 of Eq. (35) in the general form
of Eq. (35) in the general form 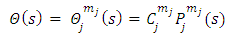
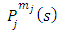 function is the solution Legendre's equation Eq. (35) for the half-integers quantum numbers
function is the solution Legendre's equation Eq. (35) for the half-integers quantum numbers 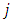 and
and 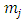
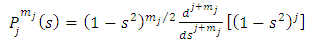
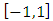 we must permit for
we must permit for 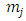 only the values
only the values 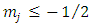 . The constants
. The constants 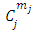 are the multiplication factors determined by the normalization condition which gives
are the multiplication factors determined by the normalization condition which gives 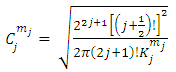
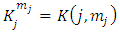 coefficients is given by the formula
coefficients is given by the formula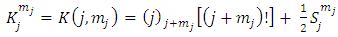
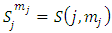 have the expression
have the expression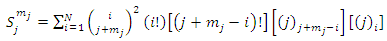
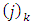 are given by the expressions
are given by the expressions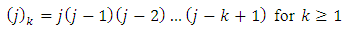
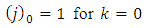
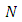 upper limit of the sum from Eq. (59) is
upper limit of the sum from Eq. (59) is 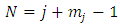 and the symbols
and the symbols 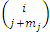 are combinations of
are combinations of 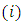 from a set of
from a set of 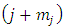 (the binomial coefficients).
(the binomial coefficients). 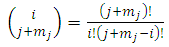
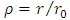 where
where 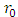 is the unit length or radius of the first Bohr orbit
is the unit length or radius of the first Bohr orbit 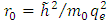 . Thus, we obtain the radial equation Eq. (28) for the Hydrogenic atom as
. Thus, we obtain the radial equation Eq. (28) for the Hydrogenic atom as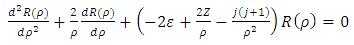
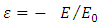 and
and 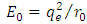 is known as the energy unit. We assumed now a solution of the form
is known as the energy unit. We assumed now a solution of the form 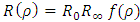 to this equation, where we have
to this equation, where we have 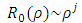 and
and 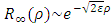 as asymptotic solutions of radial equation. Further, for generality, we can write
as asymptotic solutions of radial equation. Further, for generality, we can write 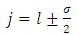
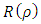 into radial equation Eq. (63), we find the equation for the unknown radial function
into radial equation Eq. (63), we find the equation for the unknown radial function 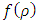
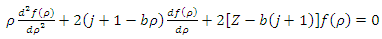
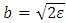 . We can simplify this equation if we introduce a new variable with no units
. We can simplify this equation if we introduce a new variable with no units 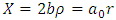 where
where 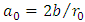 so that we can write our differential equation as
so that we can write our differential equation as 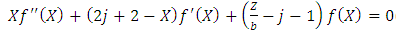
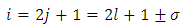
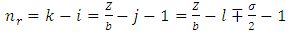
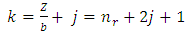
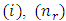 and
and 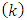 must be integers. So we can bring the equation to the following final form
must be integers. So we can bring the equation to the following final form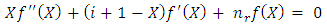
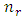
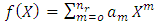 which leads us to following recursion relation between coefficients
which leads us to following recursion relation between coefficients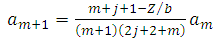
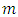 is the degree of the polynomial, we find the condition
is the degree of the polynomial, we find the condition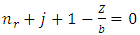
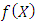 is the same well-known generalized (associated) Laguerre polynomial
is the same well-known generalized (associated) Laguerre polynomial 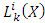 . So, the radial wave function
. So, the radial wave function 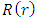 may be written as follows
may be written as follows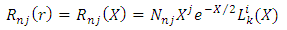
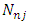 are the multiplication factors, whose expression can be determined by the normalization condition of the wave function
are the multiplication factors, whose expression can be determined by the normalization condition of the wave function 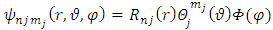 which leads us to the following equation
which leads us to the following equation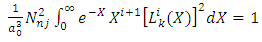
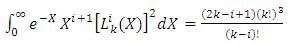
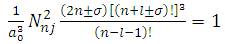
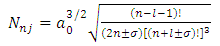
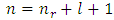 , we get the formulas
, we get the formulas 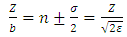
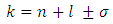
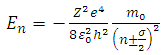
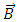 in the evolution of this type of atom are taken into account through the dimensionless variable
in the evolution of this type of atom are taken into account through the dimensionless variable 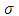 . From the above definitions of the indices
. From the above definitions of the indices 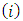 and
and 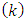 , in which this variable plays an important role, we deduce that it must be an integer. Also, we can observe that there is a relationship between the variable
, in which this variable plays an important role, we deduce that it must be an integer. Also, we can observe that there is a relationship between the variable 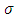 and velocity of the electron
and velocity of the electron 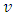 , according to the formula Eq. (30). From this formula we can deduce that the number
, according to the formula Eq. (30). From this formula we can deduce that the number 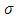 must be positive. Also, from the condition
must be positive. Also, from the condition 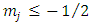 , we get
, we get 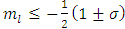 . As well, from Eq. (53), we can find the inequality
. As well, from Eq. (53), we can find the inequality 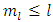 . Further, from these inequalities we get the condition
. Further, from these inequalities we get the condition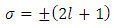
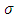 variable is an positive integer
variable is an positive integer 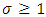 . So, we can observe that for
. So, we can observe that for 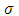 odd, although the electron spin stands out, the total energy formula does not correspond to the experimental results. This weakness of the model is certainly due to the fact that he does not take into account the radiative reaction force (the self force) which acts on the electron. Howbeit, if we admit that
odd, although the electron spin stands out, the total energy formula does not correspond to the experimental results. This weakness of the model is certainly due to the fact that he does not take into account the radiative reaction force (the self force) which acts on the electron. Howbeit, if we admit that 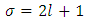 and we rewrite the radial equation Eq. (28) as follows
and we rewrite the radial equation Eq. (28) as follows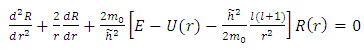
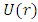 of the atom, as
of the atom, as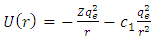
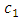 is a positive constant
is a positive constant 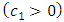 . Indeed, taking into consideration the expressions of the quantum numbers,
. Indeed, taking into consideration the expressions of the quantum numbers, 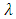 and
and 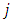 from Eqs. (46) and (64), we obtain the equation
from Eqs. (46) and (64), we obtain the equation 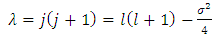
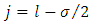 . Therefore, we can identify the second term of this equation as
. Therefore, we can identify the second term of this equation as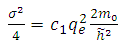
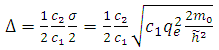
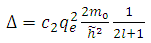
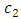 is a positive constant, too. These formulas are the experimental formulas of the alkali atoms. For these atoms the energy eigenvalues are in accordance with the expression Eq. (80), for
is a positive constant, too. These formulas are the experimental formulas of the alkali atoms. For these atoms the energy eigenvalues are in accordance with the expression Eq. (80), for 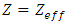 . Also, it can be shown that if we take
. Also, it can be shown that if we take 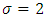 , and we introduce the formulas
, and we introduce the formulas 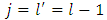 ,
, 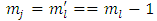 ,
, 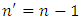 , can be obtained a theoretical situation in agreement with the results of the Stern-Gerlach experiment. The expression of the electron energy eigenvalues, for
, can be obtained a theoretical situation in agreement with the results of the Stern-Gerlach experiment. The expression of the electron energy eigenvalues, for 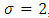 , can be written as
, can be written as 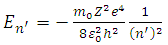
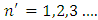 becomes principal quantum number.
becomes principal quantum number.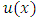 function
function 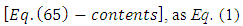
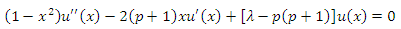 where
where 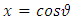 . We can look for the solution as a product between the function
. We can look for the solution as a product between the function 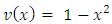 , raised to a power
, raised to a power 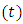 , and a power series in
, and a power series in 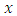
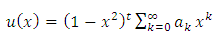
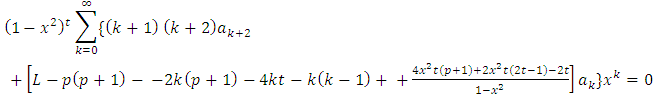
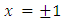 . In order to exclude them, we rewrite the numerator of the fraction as
. In order to exclude them, we rewrite the numerator of the fraction as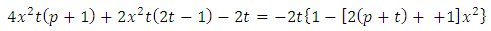
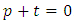 . Therefore, we get for the power
. Therefore, we get for the power 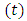 the values
the values 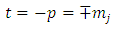
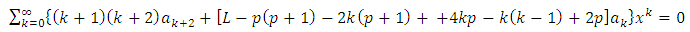
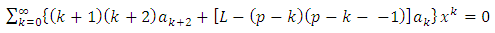
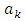
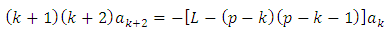
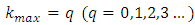 . Therefore, the recurrence relation Eq. (8) leads us to the formula
. Therefore, the recurrence relation Eq. (8) leads us to the formula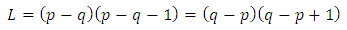 which can be written as
which can be written as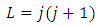
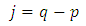
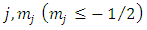
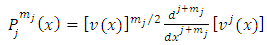
 has the expression
has the expression 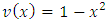 and is defined over the range
and is defined over the range 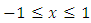 , we can show the orthogonality of
, we can show the orthogonality of 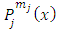 functions with the same superscript
functions with the same superscript 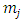 , but different subscripts
, but different subscripts 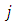 and
and 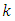
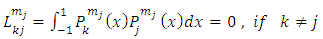
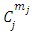 , when the indices
, when the indices 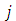 and
and 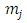 are half-integers numbers. Substituting the solutions Eq. (1) in the integral Eq. (3), we get
are half-integers numbers. Substituting the solutions Eq. (1) in the integral Eq. (3), we get 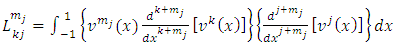
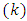 and
and 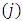 occur symmetrically and, therefore, without loss of generality, it is enough to investigate the case
occur symmetrically and, therefore, without loss of generality, it is enough to investigate the case 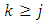 . We use now the formula of integration by parts
. We use now the formula of integration by parts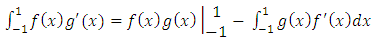
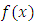 the first bracket, and by
the first bracket, and by 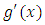 the two
the two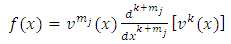
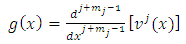
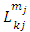
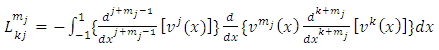
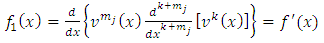
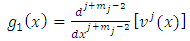
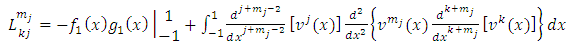
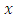 derivative of
derivative of 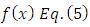 , we obtain
, we obtain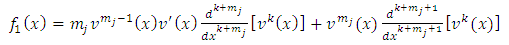
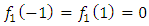 if
if 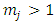 , so the integrated term will be zero, because it contains the
, so the integrated term will be zero, because it contains the 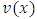 factor to a minimum power,
factor to a minimum power, 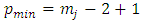 (where number 2 indicates the number of integrations), and the same
(where number 2 indicates the number of integrations), and the same 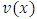 factor to a maximum power,
factor to a maximum power, 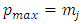 , and therefore, this factor will be zero at both endpoints
, and therefore, this factor will be zero at both endpoints 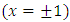 . Continuing the integration by parts, we can see that the degree of the derivative of the
. Continuing the integration by parts, we can see that the degree of the derivative of the 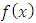 increases by 1 on each integration, while the degree of the derivative of the
increases by 1 on each integration, while the degree of the derivative of the 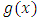 is reduced by 1 on each integration. After a number of
is reduced by 1 on each integration. After a number of 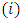 integrations by parts, the
integrations by parts, the 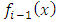 factor of the integrated term will be composed from a sum of terms which will include the
factor of the integrated term will be composed from a sum of terms which will include the 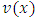 factor at the half-integers powers which extend from
factor at the half-integers powers which extend from 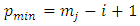 to
to 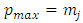 . All these terms will be zero at both endpoints, if
. All these terms will be zero at both endpoints, if 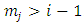 . So, after a number of
. So, after a number of 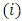 integrations by parts we can write the expression of
integrations by parts we can write the expression of 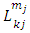 Eq. (7) as follows
Eq. (7) as follows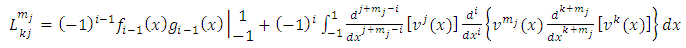
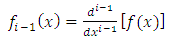
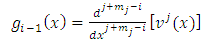
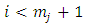 , the
, the 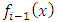 factor of integrated term will be zero. For
factor of integrated term will be zero. For 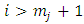 , this factor will no longer be zero. However, this time will be zero the second factor of product,
, this factor will no longer be zero. However, this time will be zero the second factor of product, 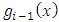 , because, after we calculate higher and higher derivatives, we will have a sum of terms containing the
, because, after we calculate higher and higher derivatives, we will have a sum of terms containing the 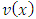 function as factor, and the lowest power of
function as factor, and the lowest power of 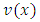 in any of these terms will be
in any of these terms will be 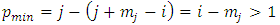 so that every term will go to zero at the endpoints. Therefore, if we integrate by parts
so that every term will go to zero at the endpoints. Therefore, if we integrate by parts 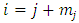 times, we get
times, we get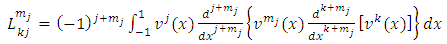
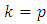 , since
, since 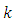 and
and  appeared symmetrically in the initial integral, we may write
appeared symmetrically in the initial integral, we may write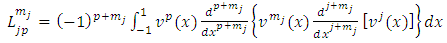
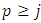 , which covers all possible cases. Further we can write the
, which covers all possible cases. Further we can write the 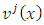 function as follows
function as follows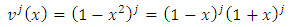
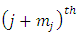 derivative of this function of the form
derivative of this function of the form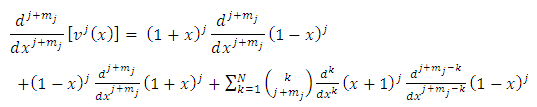
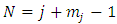 . Since each derivative of the function
. Since each derivative of the function 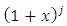 brings down the exponent and then reduces the exponent by 1, we may write
brings down the exponent and then reduces the exponent by 1, we may write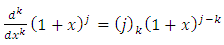
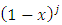 , we may also write
, we may also write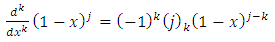
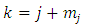 into Eqs. (21) and (22), we obtain
into Eqs. (21) and (22), we obtain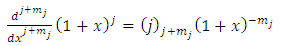
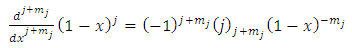
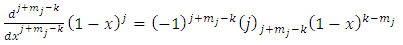
 , we obtain
, we obtain 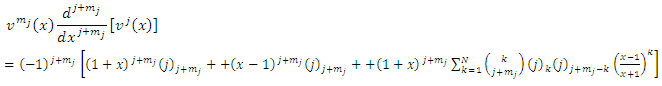
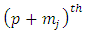 derivative of this expression, we get
derivative of this expression, we get 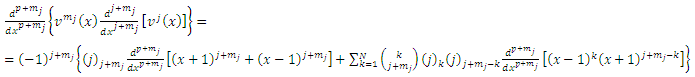
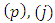 and
and 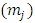 are half-integers numbers, the numbers
are half-integers numbers, the numbers 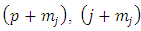 and
and 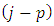 will be integers . Therefore, we can introduce the following higher derivatives formulas
will be integers . Therefore, we can introduce the following higher derivatives formulas 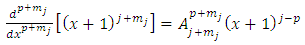
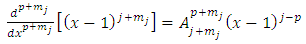
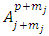 are the permutations of
are the permutations of 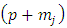 from a set of
from a set of 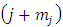
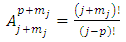
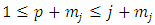 . Also, we can use now the inequality
. Also, we can use now the inequality 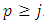 . Adding the
. Adding the 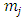 in the both members of this inequality, we get
in the both members of this inequality, we get 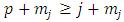 . From these inequalities we find the condition
. From these inequalities we find the condition 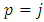 . Applying again the Leibniz's rule, further we may write
. Applying again the Leibniz's rule, further we may write 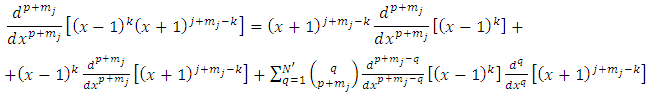
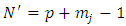 . Since
. Since 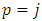 , the index
, the index 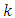 is an integer in the range
is an integer in the range 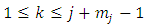 . Therefore, the first two terms of this equation will be zero. So, we can write
. Therefore, the first two terms of this equation will be zero. So, we can write 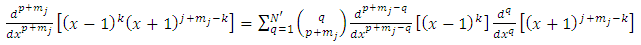
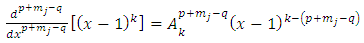
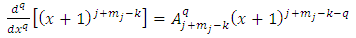
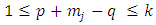
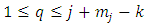
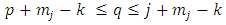
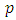 and
and 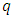 , the conditions
, the conditions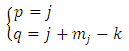
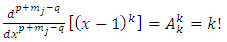
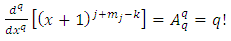
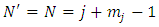 . Therefore, the expression Eq. (30) takes the final form
. Therefore, the expression Eq. (30) takes the final form 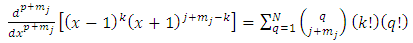
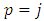 . For
. For 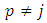 will be zero. Also, for
will be zero. Also, for 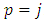 , Eqs. (26) and (27) becomes
, Eqs. (26) and (27) becomes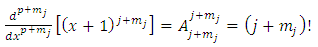
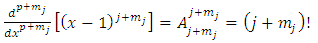
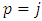 ,
, 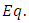 (25) can be written as
(25) can be written as 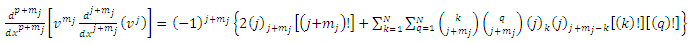
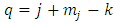 and we take into consideration the relations
and we take into consideration the relations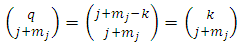
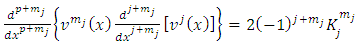
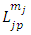 Eq. (16) takes the following form
Eq. (16) takes the following form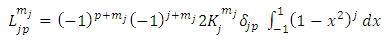
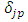 that shows the orthogonality of functions
that shows the orthogonality of functions 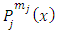 with
with 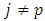 . Thus, for
. Thus, for 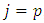 , the integral
, the integral 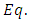 (45) becomes
(45) becomes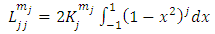
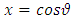 and the trigonometric formula
and the trigonometric formula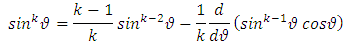 After an integration by parts, the integral can be written as
After an integration by parts, the integral can be written as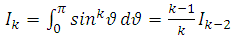
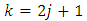 . Therefore, we can establish the following formula
. Therefore, we can establish the following formula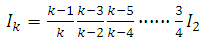
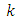 is an even number, we can write
is an even number, we can write 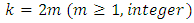 and the integral
and the integral 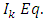 (48) becomes
(48) becomes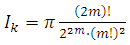
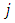 , the integral gets the formula
, the integral gets the formula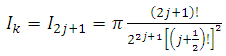
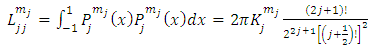
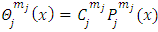 , we obtain
, we obtain 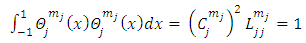
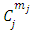 as follows
as follows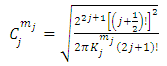
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML