Takaaki Shirahata
Laboratory of Pharmaceutical Education, Kagawa School of Pharmaceutical Sciences, Tokushima Bunri University, Shido, Japan
Correspondence to: Takaaki Shirahata, Laboratory of Pharmaceutical Education, Kagawa School of Pharmaceutical Sciences, Tokushima Bunri University, Shido, Japan.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Komendantov and Kononenko proposed a mathematical model of snail RPa1 neurons, which was described by a system of nonlinear ordinary differential equations based on the Hodgkin–Huxley formalism. This model shows bistability between regular bursting and chaotic spiking. A transient current pulse can switch the dynamical state of the model from regular bursting to chaotic spiking and vice versa. This study performed a numerical simulation analysis of the model to show the dependence of the switching from regular bursting to chaotic spiking on the amplitude, duration, and phase of the current pulse.
Keywords:
Nonlinear Dynamics, Hodgkin–Huxley Model, Bistability, Chaos
Cite this paper: Takaaki Shirahata, Numerical Simulation of Bistability between Regular Bursting and Chaotic Spiking in a Mathematical Model of Snail Neurons, International Journal of Theoretical and Mathematical Physics, Vol. 5 No. 5, 2015, pp. 145-150. doi: 10.5923/j.ijtmp.20150505.08.
1. Introduction
Chaos is an important research topic in the fields of applied mathematics (page 118 in [1]) and mathematical and theoretical physics (page 382 in [2] and page 85 in [3]). Aihara [4] reports that the Hodgkin–Huxley model, one of the most widely accepted mathematical models that describe electrical excitability of neurons, can generate chaotic oscillations. The Hodgkin–Huxley model is a system of highly nonlinear ordinary differential equations (ODEs) and is an important mathematical model of nonlinear dynamics ([5] and page 160 in [6]). In addition, chaotic oscillations are observed in various mathematical models of neurons, which are described by a system of nonlinear ODEs based on the Hodgkin–Huxley formalism. Examples include models of onchidium neurons (Figure 12 in [7]), leech interneurons (Figure 3 in [8] and Figure 10 in [9]), and snail RPa1 neurons (Figures 2, 8, and 9 in [10]).Chaotic activity observed in a mathematical model of RPa1 neurons possesses a unique feature: chaotic spiking coexists with regular bursting under certain conditions (bistability). This concept is illustrated in Figure 9 in [10], which shows that a transient depolarizing current pulse switches the activity mode of the model from chaotic spiking to regular bursting. The paper also describes that a transient hyperpolarizing current pulse switches the activity mode in the other direction, i.e., from regular bursting to chaotic spiking (see the last sentence of the results section in page 227 in [10]). However, the paper did not investigate how variations in stimulus characteristics such as amplitude, duration, and timing (i.e., phase) of the current pulse affect the switching from regular bursting to chaotic spiking.Bistability is also observed in a leech interneuron model [11]. Barnett et al. showed that the switching of the dynamical states depends on the amplitude and timing of the current pulse (Figure 2 in [11]), indicating that investigating pulse characteristics is important to assess the multistability of a neuron model. Therefore, the present study performed numerical studies of a snail RPa1 neuron model to characterize the amplitude, duration, and timing of the current pulse necessary for the switching from regular bursting to chaotic spiking.
2. Materials and Methods
A mathematical model of the snail RPa1 neurons used here was developed by Komendantov and Kononenko [10] and is described by a system of nonlinear ODEs based on the Hodgkin–Huxley formalism. The model consists of eight state variables: the membrane potential of RPa1 neurons [V (mV)], six gating variables of ionic currents (mB, hB, m, h, n, and mCa), and the intracellular calcium concentration {[Ca] (mM)}. The time evolution of these state variables is described by the following equation. 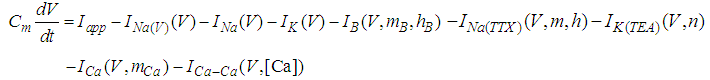 | (1) |
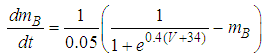 | (2) |
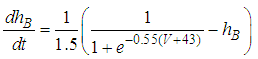 | (3) |
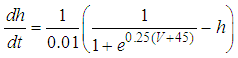 | (5) |
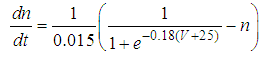 | (6) |
 | (7) |
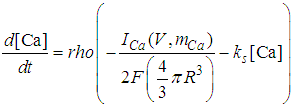 | (8) |
Here, Cm is the membrane capacitance (0.02 μF), Iapp is the current pulse with constant amplitude (Iapp values are varied in this study), INa(V) (V) is the sodium current with a voltage-dependent conductance, INa (V) is the sodium current with a voltage-independent conductance, IK (V) is the potassium current with voltage-independent conductance, IB(V, mB, hB) is the chemosensitive B current, INa(TTX)(V, m, h) is the tetrodotoxin (TTX)-sensitive sodium current, IK(TEA)(V, n) is the tetraethylammonium (TEA)-sensitive potassium current, ICa(V, mCa) is the inward calcium current, and ICa-Ca(V, [Ca]) is the calcium-inhibited calcium current. These currents are defined in Equations (9)(16) below. Rho is an endogenous calcium buffer capacity (0.002), F is the Faraday constant (96485 C/mol), R is the cell radius (0.1 mm), ks is the rate constant of intracellular calcium uptake by intracellular calcium stores (50 s−1).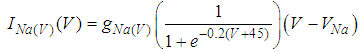 | (9) |
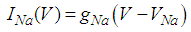 | (10) |
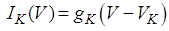 | (11) |
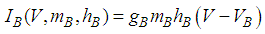 | (12) |
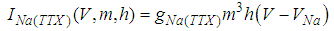 | (13) |
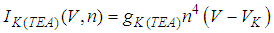 | (14) |
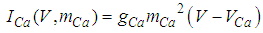 | (15) |
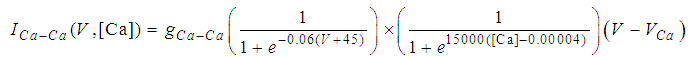 | (16) |
Here, gNa(V) (= 0.11 μS), gNa (= 0.0231 μS), gK (= 0.25 μS), gB (= 0.1372 μS), gNa(TTX) (= 400 μS), gK(TEA) (= 10 μS), gCa (= 1.5 μS), and gCa-Ca (= 0.02 μS) are maximal conductances of INa(V) (V), INa (V), IK (V), IB(V, mB, hB), INa(TTX)(V, m, h), IK(TEA)(V, n), ICa(V, mCa), and ICa-Ca(V, [Ca]), respectively. VNa (= 40 mV), VK (= −70 mV), VB (= −58 mV), and VCa (= 150 mV) are reversal potentials of sodium currents (INa(V) (V), INa (V), and INa(TTX)(V, m, h)); potassium currents (IK (V) and IK(TEA)(V, n)); IB(V, mB, hB); and calcium currents (ICa(V, mCa) and ICa-Ca(V, [Ca])), respectively. Detailed explanations of the model are provided in [10]. The free and open source software Scilab (http://www.scilab.org/) was used to numerically solve the model.
3. Results
The model of the snail RPa1 neurons shows several dynamical states by varying the value of gB (Figure 5 in [10]). However, throughout the simulation, we fixed gB at 0.1372 μS, which corresponds to the chaotic mode. The ODEs that can show multistability demonstrate several qualitatively different solutions depending on the initial conditions. For example, since the ODEs of the current study represent a bistable system, two qualitatively different solutions can be obtained. When the initial condition is V = −42 mV, mB = 0.95, hB = 0.77, m = 0.14, h = 0.1, n = 0.048, mCa = 0.0002, [Ca] = 7.0 × 10−5 mM and no transient current pulse is applied (Iapp = 0), the model shows chaotic spiking (Figure 1A). However, when the initial value of [Ca] is increased to [Ca]init = 13.0 × 10−5 mM, the model shows regular bursting (Figure 1B). Figure 1C is an expansion of Figure 1B, which illustrates the definition of the characteristics of regular bursting. An active phase of regular bursting is defined as the period of repetitive spiking, whereas a silent phase is defined as the period of nonspiking. Injection of a current pulse, i.e., hyperpolarizing input, is started at an early, intermediate, or late phase of the silent phase ((1), (2), or (3), respectively) or an early, intermediate, or late phase of the active phase ((4), (5), or (6), respectively) (Figures 2 and 3).Next, the simulations for evaluating the effect of variations in the amplitude, duration, and timing of the current pulse (Iapp) on the model dynamics are performed under initial conditions: V = −42 mV, mB = 0.95, hB = 0.77, m = 0.14, h = 0.1, n = 0.048, mCa = 0.0002, and [Ca] = 13.0 × 10−5 mM. The responses to the current pulse differed on the basis of the pulse amplitude, duration, and timing (Figure 2). When the current pulse with an amplitude of −0.5 nA and duration of 15 s is applied at an intermediate phase of an active phase (Figure 2A), the model shows a resetting behavior similar to that shown in Figure 3 in [12]. In other words, the current pulse did not switch the dynamical state of the model from regular bursting to chaotic spiking. When the current pulse with an amplitude of −0.5 nA and duration of 12 s is applied at an early phase of the active phase (Figure 2B), the model shows a transient irregular spiking behavior, after which the dynamical state returned to regular bursting. Again, in this case, the current pulse did not switch the dynamical state of the model from regular bursting to chaotic spiking. However, when the current pulse with an amplitude of −0.5 nA and duration of 15 s is applied at an early phase of the silent phase (Figure 2C), the model shows the switching from regular bursting to chaotic spiking.The results showing the dependence of the switching from regular bursting to chaotic spiking on the amplitude, duration, and timing of the current pulse are summarized in Figure 3. Figure 3A shows that the switching depends on the duration and timing of the current pulse at a fixed pulse amplitude (−0.5 nA), whereas Figure 3B shows that the switching depends on the amplitude and timing of the current pulse at a fixed pulse duration (15 s). Figure 3 shows that the conditions in which the switching from regular bursting to chaotic spiking occurs are highly complex. 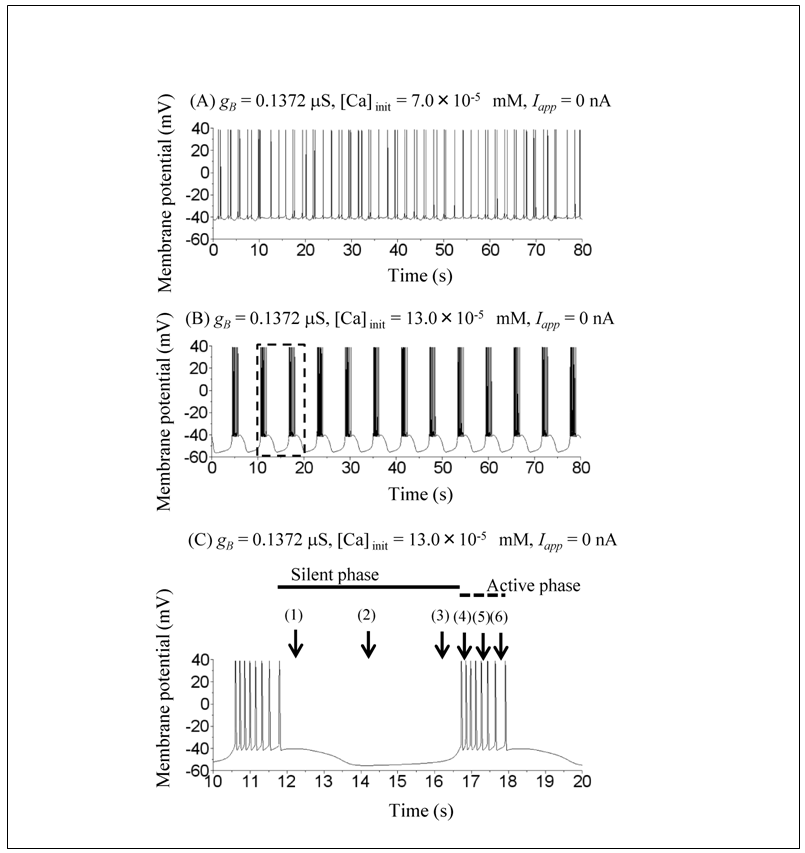 | Figure 1. Time courses of simulated membrane potentials of the RPa1 neuron model under different initial conditions. (A) Initial conditions were V = −42 mV, mB = 0.95, hB = 0.77, m = 0.14, h = 0.1, n = 0.048, mCa = 0.0002, and [Ca] = 7.0 × 10−5 mM. (B) Initial conditions were V = −42 mV, mB = 0.95, hB = 0.77, m = 0.14, h = 0.1, n = 0.048, mCa = 0.0002, and [Ca] = 13.0 × 10−5 mM. (C) The dashed square in (B) was expanded. Active and silent phases of regular bursting were explained. Current pulse injections in Figures 2 and 3 started at either (1) or (6) |
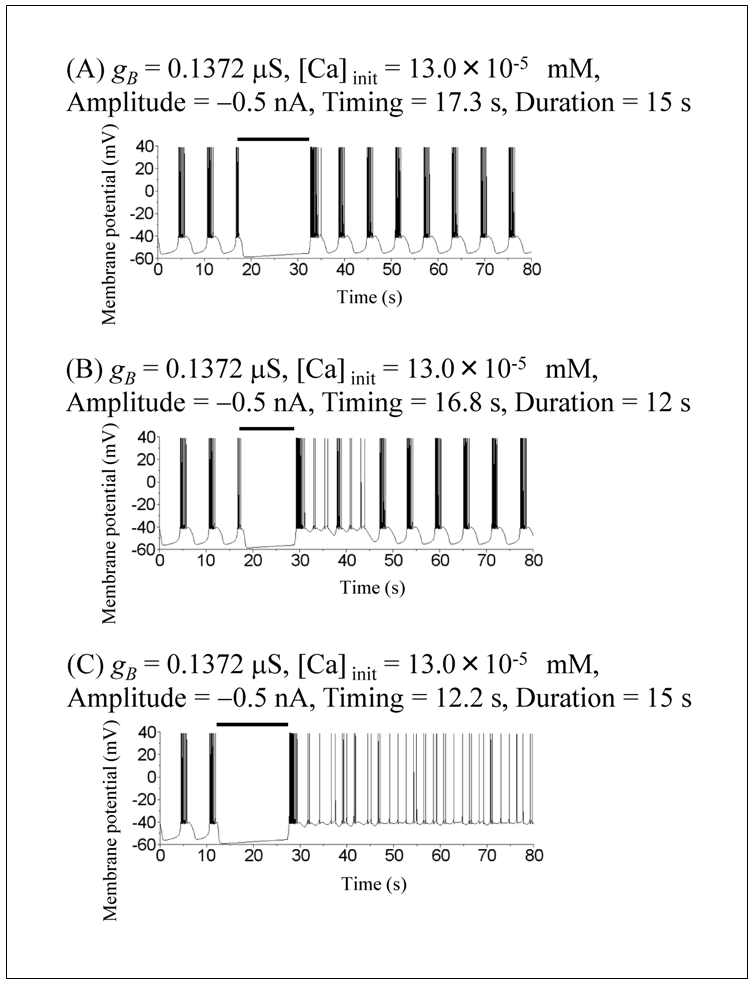 | Figure 2. Simulated responses to current pulse injections under different pulse conditions. The amplitude, timing, and duration of the pulses were (A) −0.5 nA, 17.3 s, and 15 s, (B) −0.5 nA, 16.8 s, and 12 s, and (C) −0.5 nA, 12.2 s, and 15 s, respectively. Horizontal bars indicate the period during which the pulses were applied |
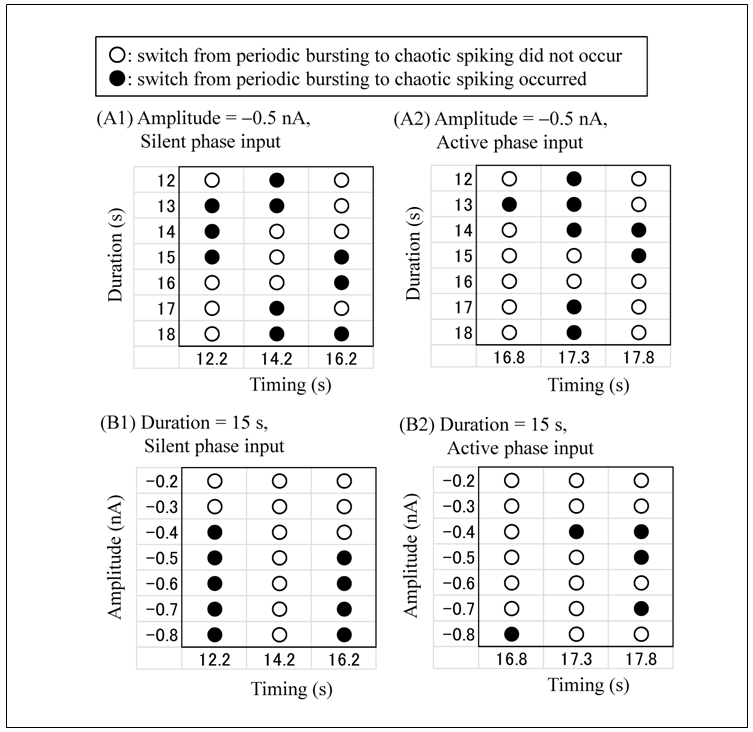 | Figure 3. Summary of the pulse characteristics necessary for the switching from regular bursting to chaotic spiking. (A) The pulse amplitude was fixed at −0.5 nA. Pulse injections started at a silent phase (A1) or an active phase (A2). (B) The pulse duration was fixed at 15 s. Pulse injections started at a silent phase (B1) or an active phase (B2). White circle: switching did not occur. Black circle: switching occurred |
4. Discussions
This study investigated the effect of the current pulse on the dynamics of the snail RPa1 neuron model and revealed pulse characteristics that induced the switching from regular bursting to chaotic spiking. A previous study described that the current pulse with an amplitude of −0.5 nA and duration of 15 s induced the switching from regular bursting to chaotic spiking (page 227 in [10]). However, that study did not clarify whether the switching depended on the timing of the current pulses. The present study showed the importance of the timing of the current pulse as the switching is influenced by not only the pulse amplitude and duration but also the timing of the current pulse (Figure 3).The responses to the current pulse have been studied in other neuron and endocrine cell models [11-13]. In a pre-Bötzinger complex neuron model, the hyperpolarizing current pulse applied during the active phase of regular bursting induced the resetting behavior (Figure 3 in [12]). Although a similar resetting behavior was also observed in the present study (Figure 2A), the RPa1 neuron model was more complex than the pre-Bötzinger complex neuron model because the former can exhibit the resetting behavior (Figure 2A) as well as the switching from regular bursting to chaotic spiking (Figure 2C) depending on pulse characteristics. In an endocrine cell model, the resetting behavior was induced by the depolarizing current pulse (Figure 9 in [13]); however, bistability corresponding to that of the RPa1 neuron model was not reported. The present study focused on the switching from regular bursting to chaotic spiking. In contrast, the bistability reported in a leech interneuron model was between regular bursting and silence [11]. Interestingly, pulse characteristics necessary for the switching differed between the two models. The amplitude ranges for the switching at an early phase overlapped with those at a late phase in the snail model (Figure 3B1) but not in the leach model (Figures 2 and 5 in [11]).
5. Conclusions
The present study showed that under certain conditions, the snail RPa1 neuron model do not switch from regular bursting to chaotic spiking. Therefore, it is important to regulate appropriately the pulse characteristics such as the pulse amplitude, duration, and timing of the current pulse.
ACKNOWLEDGEMENTS
The author would like to thank Enago (www.enago.jp) for the English language review.
References
| [1] | G. B. Ermentrout and D. H. Terman, Mathematical Foundations of Neuroscience, Interdisciplinary Applied Mathematics, vol. 35, Springer, New York, 2010. |
| [2] | C. W. Wong, Introduction to Mathematical Physics: Methods & Concepts, Oxford University Press, Oxford, 2013. |
| [3] | U. Krey and A. Owen, Basic Theoretical Physics, Springer, Berlin, 2007. |
| [4] | K. Aihara (2008), “Chaos in neurons,” Scholarpedia, 3(5): 1786. |
| [5] | T. Shirahata, “Numerical Study of a Mathematical Model of Vibrissa Motoneurons: The Relationship between Repetitive Spiking and Two Types of Sodium Conductance”, International Journal of Theoretical and Mathematical Physics, vol. 5, no. 3, pp. 48-52, 2015. |
| [6] | A. Fuchs, Nonlinear Dynamics in Complex Systems, Springer, Heidelberg, 2013. |
| [7] | H. Hayashi and S. Ishizuka, “Chaotic nature of bursting discharges in the Onchidium pacemaker neuron,” Journal of Theoretical Biology, vol. 156, no. 3, pp. 269-291, 1992. |
| [8] | G. Cymbalyuk and A. Shilnikov, “Coexistence of tonic spiking oscillations in a leech neuron model,” Journal of Computational Neuroscience, vol. 18, no. 3, pp. 255-263, 2005. |
| [9] | A. Shilnikov, R. L. Calabrese, and G. Cymbalyuk, “Mechanism of bistability: Tonic spiking and bursting in a neuron model,” Physical Review E, vol. 71, pp. 056214, 2005. |
| [10] | A. O. Komendantov and N. I. Kononenko, “Deterministic chaos in mathematical model of pacemaker activity in bursting neurons of snail, Helix Pomatia,” Journal of Theoretical Biology, vol. 183, no. 2, pp. 219-230, 1996. |
| [11] | W. Barnett, G. O’Brien, and G. Cymbalyuk, “Bistability of silence and seizure-like bursting,” Journal of Neuroscience Methods, vol. 220, no. 2, pp. 179-189, 2013. |
| [12] | T. Shirahata, “The effect of hyperpolarizing inputs on the dynamics of a bursting pacemaker neuron model in the pre-Bötzinger complex,” Neuroscience Letters, vol. 473, no. 1, pp. 16-21, 2010. |
| [13] | J. V. Stern, H. M. Osinga, A. LeBeau, and A. Sherman, “Resetting behavior in a model of bursting in secretory pituitary cells: distinguishing plateaus from pseudo-plateaus,” Bulletin of Mathematical Biology, vol. 70, no. 1, pp. 68-88, 2008. |


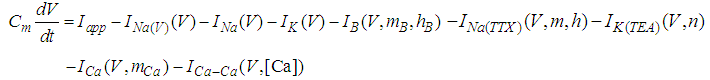
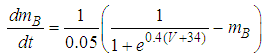
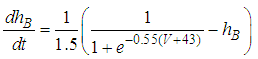
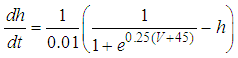
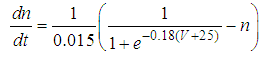

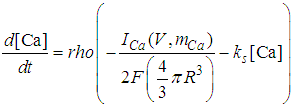
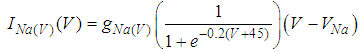
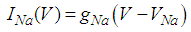
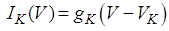
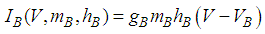
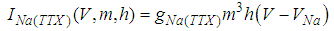
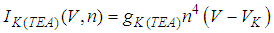
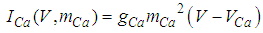
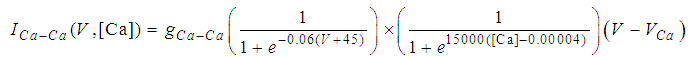
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML

