Danladi Eli1, Gyuk P. M.2
1Department of Physics, Nigerian Defence Academy, Kaduna, Nigeria
2Department of Physics, Kaduna State University, Kaduna, Nigeria
Correspondence to: Danladi Eli, Department of Physics, Nigerian Defence Academy, Kaduna, Nigeria.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
A general solution for transverse magnetization, the nuclear magnetic resonance (NMR) signals for diffusion-advection equation with spatially varying velocity and diffusion coefficients, which is based on the fundamental Bloch NMR flow equations, was obtained using the method of separation of variable. It assumed that the velocity component is proportional to the coordinate and that the diffusion coefficient is proportional to the square of the corresponding component. There is a simple transformation which reduces the spatially variable equation to a constant coefficient. After some assumptions, the 3-D equation degenerates to a 2-D problem. The solution to this equation is useful in describing physical phenomenon such as transport of materials in a fluid. The result obtained in this study can have applications in functional magnetic resonance imaging (fMRI) with more accurate information.
Keywords:
NMR diffusion advection equation, Diffusion coefficient, Separation of variable, Magnetic resonance imaging (MRI)
Cite this paper: Danladi Eli, Gyuk P. M., Analytical Solution to Diffusion-Advection Equation in Spherical Coordinate Based on the Fundamental Bloch NMR Flow Equations, International Journal of Theoretical and Mathematical Physics, Vol. 5 No. 5, 2015, pp. 140-144. doi: 10.5923/j.ijtmp.20150505.07.
1. Introduction
To investigate the diffusion process of magnetization in a fluid moving at a uniform velocity, v, which is constant in time, we have to take the process of advection into consideration. The equation which describes such a process is known as the advection equation (Awojoyegbe et.,al, 2010). The advection equation is the partial differential equation that governs the motion of a conserved scalar as it is advected by a known velocity field. It is derived using the scalar’s conservation law, together with Gauss’s theorem, and taking the infinitesimal limit. The diffusion–advection equation (a differential equation describing the process of diffusion and advection) is obtained by adding the advection operator to the main diffusion equation. In the spherical coordinates, the advection operator is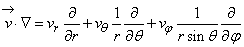 Where the velocity vector v has components
Where the velocity vector v has components 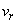 ,
,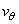 , and
, and 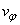 in the
in the 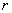 ,
, 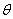 , and
, and 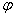 directions, respectively.
directions, respectively.
2. The NMR Diffusion Advection Equation
In accordance with Awojoyogbe et.,al 2010, The NMR diffusion–advection equation with variable coefficient could be obtained from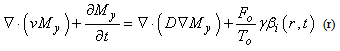 Where
Where 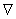 is the Del operator in the spherical coordinate system. We have to re-write the advection operator (the first term on the left hand side of Eq. (r)) because this fluid velocity is now spatially dependent. Generally speaking, the advection term for the transverse magnetization is
is the Del operator in the spherical coordinate system. We have to re-write the advection operator (the first term on the left hand side of Eq. (r)) because this fluid velocity is now spatially dependent. Generally speaking, the advection term for the transverse magnetization is 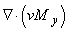 . After expansion we obtained
. After expansion we obtained 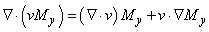 When the fluid velocity is constant,
When the fluid velocity is constant, 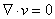 and then
and then 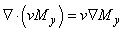 this is similar to a case of incompressible fluid in fluid dynamics.Since perfusing substances obey the advection equation, the appropriate equation to accurately describe a flow process in a spherical geometry based on equation (r).Awojoyobe el., al 2010 is
this is similar to a case of incompressible fluid in fluid dynamics.Since perfusing substances obey the advection equation, the appropriate equation to accurately describe a flow process in a spherical geometry based on equation (r).Awojoyobe el., al 2010 is | (1) |
If the parameters 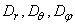 represent the diffusion coefficients, then the equation above is the equation of diffusion of magnetization as the nuclear spins move. The function
represent the diffusion coefficients, then the equation above is the equation of diffusion of magnetization as the nuclear spins move. The function 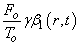 is the forcing function, which shows that the application of radio frequency (RF),
is the forcing function, which shows that the application of radio frequency (RF), 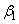 field has an influence on the diffusion of magnetization. It is interesting to note that the dimension of equation above exactly matches that of diffusion coefficient.In this paper, we are interested in getting the general solution of the equation using the method of separation of variables.If we define
field has an influence on the diffusion of magnetization. It is interesting to note that the dimension of equation above exactly matches that of diffusion coefficient.In this paper, we are interested in getting the general solution of the equation using the method of separation of variables.If we define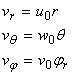 and
and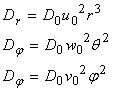 (dada et.,al 2010)Where
(dada et.,al 2010)Where 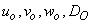 are constants (M. Dada. et.,al 2010)In each direction the velocity component has a linear dependence on the coordinates and the corresponding diffusion coefficient has a quadratic dependence on the coordinates. And if we assume
are constants (M. Dada. et.,al 2010)In each direction the velocity component has a linear dependence on the coordinates and the corresponding diffusion coefficient has a quadratic dependence on the coordinates. And if we assume 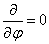 (E. Danladi et.,al 2015) then the equation above reduces to
(E. Danladi et.,al 2015) then the equation above reduces to 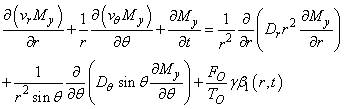 | (2) |
Differentiating equation (2) we have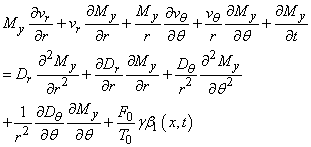 | (3) |
The transformation of equation (3) involves introducing a new variable by making some assumptions (Sprawls, 2000) | (3a) |
and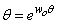 | (3b) |
From (a) we have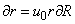 Also, from (b)
Also, from (b)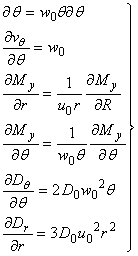 | (3c) |
Equation (3) can also be rearrange as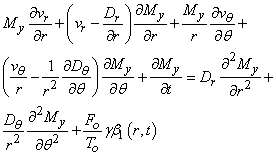 | (4) |
Substitute (c) and 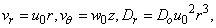
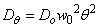 into (4) we have
into (4) we have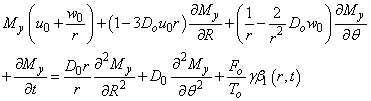 | (5) |
If we then make the assumption that 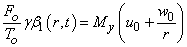 Awojoyogbe et., al 2010,Then equation (5) becomes
Awojoyogbe et., al 2010,Then equation (5) becomes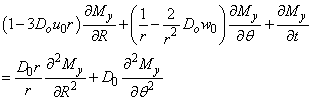 | (6) |
equation (6) can also be written as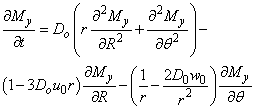 | (7) |
It is always possible to find solutions of the equation above, by separating into time and position coordinates. The method of the separation of variables relies upon the assumption that a function of the form 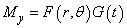 Where
Where 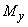 is a function of r,
is a function of r, 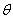 and t, and F is a function of r,
and t, and F is a function of r, 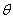 and G is a function of t alone, will be the solution to the partial differential equation above. Equation (7) can now be written as:
and G is a function of t alone, will be the solution to the partial differential equation above. Equation (7) can now be written as: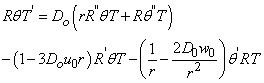 Divide through by
Divide through by 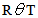
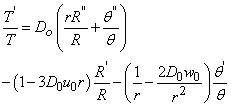 Equate both sides with a constant
Equate both sides with a constant 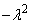 to have
to have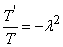 | (7) |
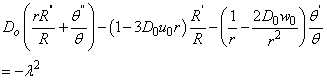 | (8) |
From (7),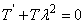 | (9) |
Let 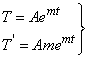 | (10) |
Putting (10) into (9) 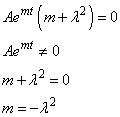 Therefore
Therefore 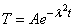 | (11) |
Also from (8)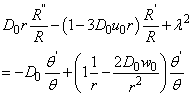 | (12) |
Equation (12) can also be separated by equating both sides with a constant 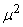 and by re-arrangement we obtain
and by re-arrangement we obtain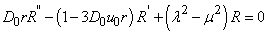 | (13) |
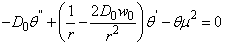 | (14) |
Equation (14) can also be written as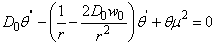 | (15) |
From (13)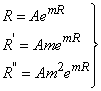 | (16) |
Substitute (16) into (13)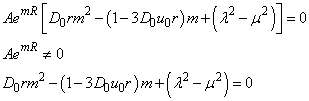
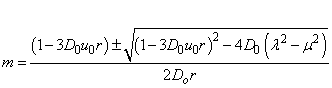 Therefore,
Therefore,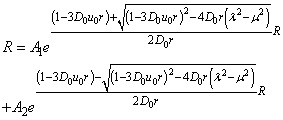 | (17) |
From (17) let 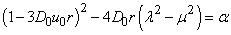 And making
And making 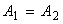 we have:
we have: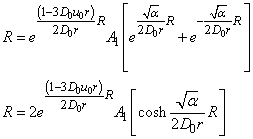 From (15), let
From (15), let 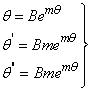 | (18) |
Put (18) into (15)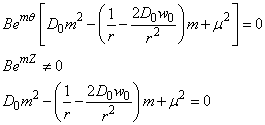
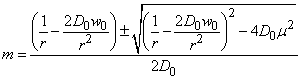 Therefore,
Therefore, 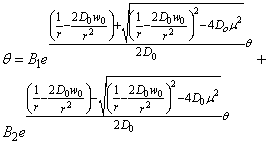 | (19) |
From (19), let 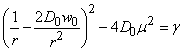
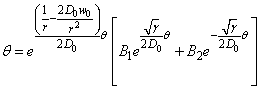 If we let
If we let 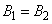 we have:
we have: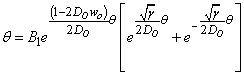 Then the transverse magnetization becomes
Then the transverse magnetization becomes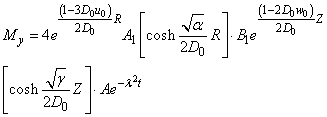 | (20) |
The solution above is the NMR transverse magnetization and signal in spherical geometry. This NMR signal is a function of diffusion coefficient 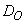 . The solution can be a tool to accurately understand the combined effect of diffusion and perfusion processes in human physiological and pathological flow systems. There seems to be evidence to suggest that in some transport processes the velocity and diffusion coefficients are not constants but functions of time and space (Zoppou and, Knight. 999).
. The solution can be a tool to accurately understand the combined effect of diffusion and perfusion processes in human physiological and pathological flow systems. There seems to be evidence to suggest that in some transport processes the velocity and diffusion coefficients are not constants but functions of time and space (Zoppou and, Knight. 999).
3. Conclusions
We have obtained basic expression for the transverse magnetization (the NMR signals) in spherical geometry based on the bloch NMR flow equations. This general solution is quite interesting and promising in the context of some recent research works on dynamical flow. The application of this fundamental solution to solve real life flow problems in which NMR-sensitive materials are transported will be presented separately.
ACKNOWLEDGEMENTS
The authors are grateful to both Mr. Dada O.M and Dr. Jiya Mohammed for their constructive comments.
References
| [1] | Awojoyogbe OB, Faromika OP, Folorunsho Dada. OM, Fuwape IA, Boubaker K (2010). Mathematical model of the Bloch NMR flow equations for the analysis of fluid flow in restricted geometries using the Boubaker polynomials expansion scheme, Curr. Appl. Phys. 10: 289-293. |
| [2] | Awojoyogbe, OB, Dada OM, Faromika OP, Dada OE (2010). Mathematical Concept of the Bloch Flow Equations for General Magnetic Resonance Imaging: A Review pg 85-101 |
| [3] | Dada OM, Awojoyogbe, Boubaker K and Ojambati OS (2010). BPES analyses of a new diffusion-advection equation for fluid flow in blood vessels under different bio-physico-geometrical conditions, Journal of Biophysics and Structural Biology Vol. 2(3), pp. 28-34. |
| [4] | Danladi E, Hycienth O (2015). Analytical solution to Diffusion-Advection Equation with Variable Velocity and Diffusion Coefficient in Cylindrical Coordinate. Submitted for publication in Nigerian Journal of Physics. |
| [5] | Sprawls P (2000). Magnetic Resonance Imaging: Principle, Methods, and Techniques. Medical Physics Publishing: Madison, Wisconsin pp. 137-144. |
| [6] | Zoppou C, Knight JH (1999). Analytical solution of spatially variable coefficient advection-diffusion equation in upto three dimensions. Applied mathematical modelling. Vol 23(9): 667-685. |
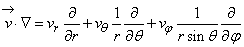 Where the velocity vector v has components
Where the velocity vector v has components 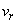 ,
,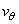 , and
, and 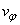 in the
in the 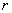 ,
, 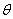 , and
, and 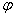 directions, respectively.
directions, respectively.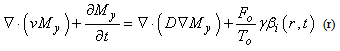 Where
Where 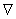 is the Del operator in the spherical coordinate system. We have to re-write the advection operator (the first term on the left hand side of Eq. (r)) because this fluid velocity is now spatially dependent. Generally speaking, the advection term for the transverse magnetization is
is the Del operator in the spherical coordinate system. We have to re-write the advection operator (the first term on the left hand side of Eq. (r)) because this fluid velocity is now spatially dependent. Generally speaking, the advection term for the transverse magnetization is 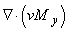 . After expansion we obtained
. After expansion we obtained 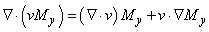 When the fluid velocity is constant,
When the fluid velocity is constant, 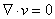 and then
and then 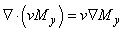 this is similar to a case of incompressible fluid in fluid dynamics.Since perfusing substances obey the advection equation, the appropriate equation to accurately describe a flow process in a spherical geometry based on equation (r).Awojoyobe el., al 2010 is
this is similar to a case of incompressible fluid in fluid dynamics.Since perfusing substances obey the advection equation, the appropriate equation to accurately describe a flow process in a spherical geometry based on equation (r).Awojoyobe el., al 2010 is
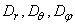 represent the diffusion coefficients, then the equation above is the equation of diffusion of magnetization as the nuclear spins move. The function
represent the diffusion coefficients, then the equation above is the equation of diffusion of magnetization as the nuclear spins move. The function 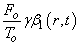 is the forcing function, which shows that the application of radio frequency (RF),
is the forcing function, which shows that the application of radio frequency (RF), 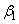 field has an influence on the diffusion of magnetization. It is interesting to note that the dimension of equation above exactly matches that of diffusion coefficient.In this paper, we are interested in getting the general solution of the equation using the method of separation of variables.If we define
field has an influence on the diffusion of magnetization. It is interesting to note that the dimension of equation above exactly matches that of diffusion coefficient.In this paper, we are interested in getting the general solution of the equation using the method of separation of variables.If we define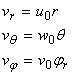 and
and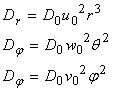 (dada et.,al 2010)Where
(dada et.,al 2010)Where 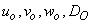 are constants (M. Dada. et.,al 2010)In each direction the velocity component has a linear dependence on the coordinates and the corresponding diffusion coefficient has a quadratic dependence on the coordinates. And if we assume
are constants (M. Dada. et.,al 2010)In each direction the velocity component has a linear dependence on the coordinates and the corresponding diffusion coefficient has a quadratic dependence on the coordinates. And if we assume 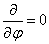 (E. Danladi et.,al 2015) then the equation above reduces to
(E. Danladi et.,al 2015) then the equation above reduces to 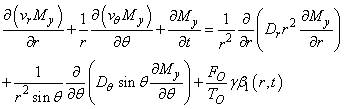
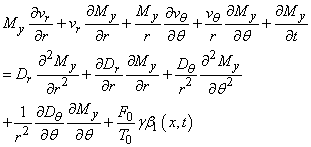
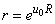
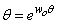
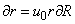 Also, from (b)
Also, from (b)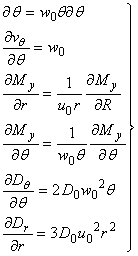
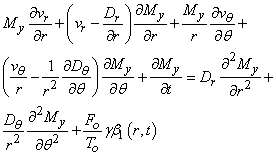
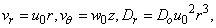
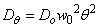 into (4) we have
into (4) we have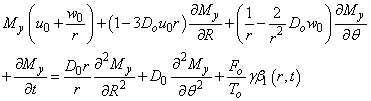
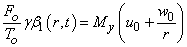 Awojoyogbe et., al 2010,Then equation (5) becomes
Awojoyogbe et., al 2010,Then equation (5) becomes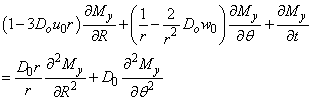
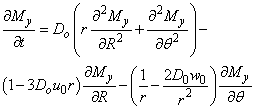
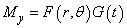 Where
Where 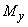 is a function of r,
is a function of r, 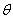 and t, and F is a function of r,
and t, and F is a function of r, 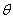 and G is a function of t alone, will be the solution to the partial differential equation above. Equation (7) can now be written as:
and G is a function of t alone, will be the solution to the partial differential equation above. Equation (7) can now be written as: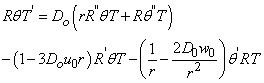 Divide through by
Divide through by 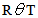
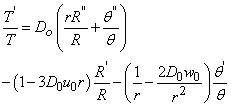 Equate both sides with a constant
Equate both sides with a constant 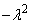 to have
to have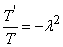
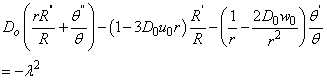
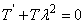
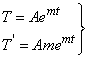
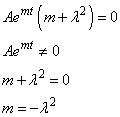 Therefore
Therefore 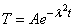
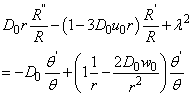
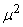 and by re-arrangement we obtain
and by re-arrangement we obtain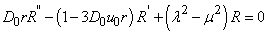
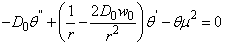
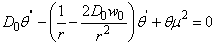
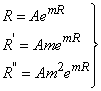
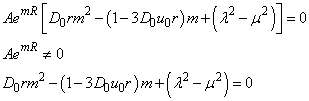
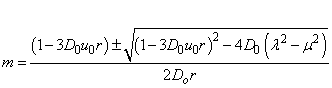 Therefore,
Therefore,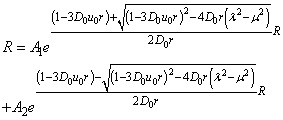
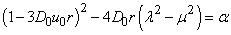 And making
And making 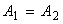 we have:
we have: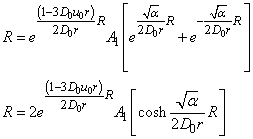 From (15), let
From (15), let 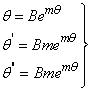
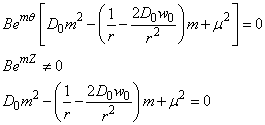
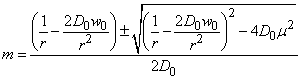 Therefore,
Therefore, 
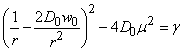
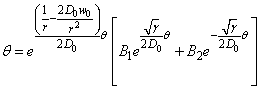 If we let
If we let 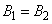 we have:
we have: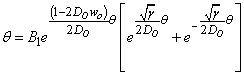 Then the transverse magnetization becomes
Then the transverse magnetization becomes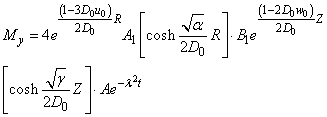
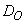 . The solution can be a tool to accurately understand the combined effect of diffusion and perfusion processes in human physiological and pathological flow systems. There seems to be evidence to suggest that in some transport processes the velocity and diffusion coefficients are not constants but functions of time and space (Zoppou and, Knight. 999).
. The solution can be a tool to accurately understand the combined effect of diffusion and perfusion processes in human physiological and pathological flow systems. There seems to be evidence to suggest that in some transport processes the velocity and diffusion coefficients are not constants but functions of time and space (Zoppou and, Knight. 999).  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML