-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2015; 5(5): 120-136
doi:10.5923/j.ijtmp.20150505.05
Two-Body Problem of Classical Electrodynamics with Radiation Terms-Derivation of Equations (I)
Vasil G. Angelov
Department of Mathematics, University of Mining and Geology “St. I. Rilski”, Sofia, Bulgaria
Correspondence to: Vasil G. Angelov, Department of Mathematics, University of Mining and Geology “St. I. Rilski”, Sofia, Bulgaria.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
This paper is the first part of our investigations devoted to the two-body problem of classical electrodynamics. The primary purpose of this first part is to derive equations of motion describing two moving charged mass particles taking into account the radiation. We proceed from the suggestions given by J. L. Synge [1]. He has proposed a formulation of the of relativistic two-body problem with usually accepted Dirac’s radiation terms [2] containing second derivatives of the velocities: 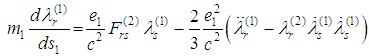 ,
, 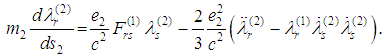 Here we propose a general approach to introduce new equations of motion based on the same Dirac’s physical assumptions from [2]. Instead of the above system of eight equations of motion we derive consider an analogous system
Here we propose a general approach to introduce new equations of motion based on the same Dirac’s physical assumptions from [2]. Instead of the above system of eight equations of motion we derive consider an analogous system 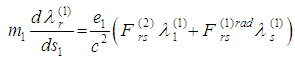 ,
, 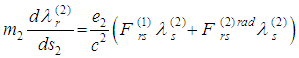 where the classical Lorentz-Dirac radiation terms are replaced by newly derived ones. We show that two equations are consequences of the rest ones and so we have to solve a system of six equations for six unknown velocities, issue that has not been discussed in the literature. Instead of second order differential system (with respect to the unknown velocities) we obtain a first order neutral system with both retarded and advanced arguments depending on the unknown trajectories. In the second part we solve the system and so we give a method for overcoming the singularities arising in Dirac radiation terms.
where the classical Lorentz-Dirac radiation terms are replaced by newly derived ones. We show that two equations are consequences of the rest ones and so we have to solve a system of six equations for six unknown velocities, issue that has not been discussed in the literature. Instead of second order differential system (with respect to the unknown velocities) we obtain a first order neutral system with both retarded and advanced arguments depending on the unknown trajectories. In the second part we solve the system and so we give a method for overcoming the singularities arising in Dirac radiation terms.
Keywords: Classical electrodynamics, Two-Body problem, Dirac-Lorentz radiation term, Neutral equations with both delay and advanced arguments, Fixed point theorem
Cite this paper: Vasil G. Angelov, Two-Body Problem of Classical Electrodynamics with Radiation Terms-Derivation of Equations (I), International Journal of Theoretical and Mathematical Physics, Vol. 5 No. 5, 2015, pp. 120-136. doi: 10.5923/j.ijtmp.20150505.05.
Article Outline
1. Introduction
- In [1] J. L. Synge has formulated a two-body problem in the frame of classical electrodynamics and has mentioned at the very end of [1] the possibility to generalize the model including Dirac radiation terms [2]. The Synge’s considerations [1] of two-body problem are based on the Lorentz ponder-motive force derived in a relativistic form by W. Pauli [3] via Lienard-Wiechert retarded potentials and adding the Dirac’s radiation terms. Our goal is, following [1], to give a unified approach of derivation of equations of motion for two-body problem with radiation terms. We propose a new mathematical formulation of the Dirac’s idea based on retarded and advanced potentials. Let us note that Dirac’s derivations lead to the second order differential equations with respect to the unknown velocities which by necessity needs prescribing of initial accelerations. A lot of papers investigate equations with usually accepted Dirac-Lorentz radiation terms [4]-[27]. In contrast of these papers following the Synge’s formalism [1] here we derive a new form of the radiation term leading to the first order neutral equations with respect to unknown velocities and introduce retarded and advanced arguments depending on unknown trajectories [28]. We note that this new term is applied in the one-dimensional case to overcome P. Ehrenfest paradox [29] and in three-dimensional case for correction of the Lorentz-Dirac equation [30]. We point out that the following difficulty arises that has not been discussed in the literature. The relativistic Lorentz – Dirac equations in the Minkowski’s space are four in number for three unknown functions. In [30] we have proved that 4-th equation is a consequence of the first three ones. An analogous problems arises in the two-body problem.The equations of motion are eight in number for six un-known functions velocities. Here we prove that the 4-th and the 8-th equation are consequence of the rest ones. In this manner we overcome a mathematical problem generated by overdetermined system. From the physical point of view, solving this system substituting the found functions in the 4-th and 8-th equations we obtain the energy balance of the moving particles.In the second part we prove an existence-uniqueness of a periodic solution of the system mentioned which means an existence of a closed orbit of two-body problem. In this way, we show that the Bohr-Sommerfeld stationary states (cf. [31], [32]) are rather implicated by the classical electrodynamics than contradict it. Here we use the technique introduced in [33], [34] and obtain a system of eight equations of motion with new form of the radiation terms:
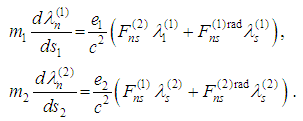 Main results are given in Section 2. Subsection 2.1 is devoted to the strict mathematical formulation of the original Dirac’s assumptions. In fact, we compare the relative and absolute times assuming that the past and future instants depend only on the present instant. In Subsection 2.2 we show that the 4-th equation is a consequence of the first three ones and the 8-th equation is a consequence of the 5-th, 6-th and 7-th ones. So we obtain a system of six equations for six unknown functions − the velocities of the moving particles. This system is of neutral type with respect to the unknown velocities with both retarded and advanced arguments depending on the unknown trajectories.Section 3 is Conclusion.Some cumbersome calculations are separated in Supplement 1 and Supplement 2.
Main results are given in Section 2. Subsection 2.1 is devoted to the strict mathematical formulation of the original Dirac’s assumptions. In fact, we compare the relative and absolute times assuming that the past and future instants depend only on the present instant. In Subsection 2.2 we show that the 4-th equation is a consequence of the first three ones and the 8-th equation is a consequence of the 5-th, 6-th and 7-th ones. So we obtain a system of six equations for six unknown functions − the velocities of the moving particles. This system is of neutral type with respect to the unknown velocities with both retarded and advanced arguments depending on the unknown trajectories.Section 3 is Conclusion.Some cumbersome calculations are separated in Supplement 1 and Supplement 2.2. Main Results
2.1. Derivation of Equations of Motion for Two-Body Problem with New Dirac Radiation Term
- The considerations are in the Minkowski’s space [3]. Roman suffixes run over 1, 2, 3, 4 while Greek – 1, 2, 3 with Einstein summation convention. We use denotations from [1]. By
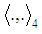 we denote the dot product in the Minkowski space, and by
we denote the dot product in the Minkowski space, and by 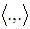 – the dot product in three-dimensional Euclidean subspace. The space-time coordinates of the moving particles are
– the dot product in three-dimensional Euclidean subspace. The space-time coordinates of the moving particles are 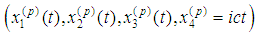
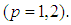 Quantities relating to the particles are denoted in the following way:
Quantities relating to the particles are denoted in the following way: 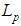 – world lines;
– world lines; 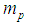 – proper masses;
– proper masses; 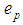 – charges. The components of unit tangent vectors to world lines are
– charges. The components of unit tangent vectors to world lines are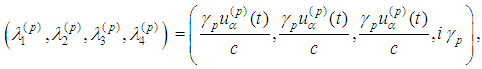
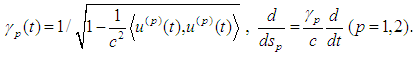 Then
Then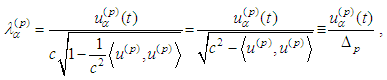
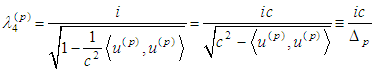 where
where 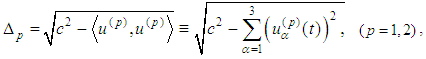 c is the vacuum speed of light and
c is the vacuum speed of light and 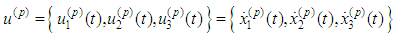 are velocities of the moving particles. The components of the accelerations are
are velocities of the moving particles. The components of the accelerations are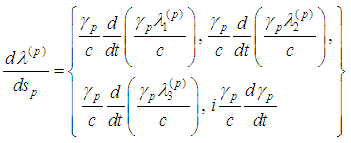 or
or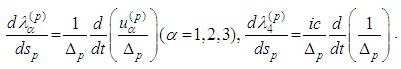 Let
Let 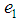 be a charge describing any curve L1 in space-time (cf. [1]). Let A2 be any event and let A1 be an intersection of L1 with the null-cone drawn into the past from A2. Let
be a charge describing any curve L1 in space-time (cf. [1]). Let A2 be any event and let A1 be an intersection of L1 with the null-cone drawn into the past from A2. Let 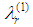 be the unit tangent vector to L1 at A1, and let
be the unit tangent vector to L1 at A1, and let 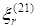 be the null-vector A1A2. Then, by hypothesis from [1], the field at A2 due to L1 is given by the retarded potential 4-vector
be the null-vector A1A2. Then, by hypothesis from [1], the field at A2 due to L1 is given by the retarded potential 4-vector 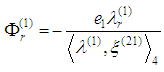 | (1) |
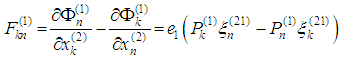 | (2) |
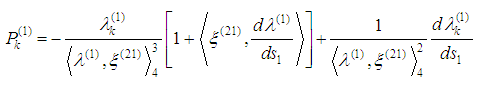 | (3) |
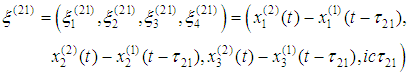 is an isotropic vector, i.e. it lies on the light-cone [1]. The world-line L2 of the charge
is an isotropic vector, i.e. it lies on the light-cone [1]. The world-line L2 of the charge 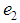 , passing through A2, satisfies the equations of motion
, passing through A2, satisfies the equations of motion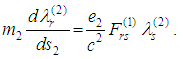 We have to add however the radiation field caused by the particle itself. Then equations of motion for the second particle are the following four ones:
We have to add however the radiation field caused by the particle itself. Then equations of motion for the second particle are the following four ones: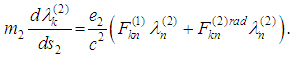 If we interchange the roles of the two world-lines we have the following equations of motion for the first particle:
If we interchange the roles of the two world-lines we have the following equations of motion for the first particle: 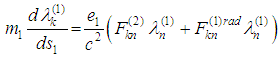 | (4) |
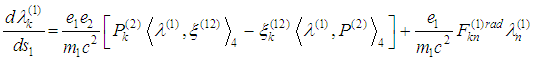 | (5) |
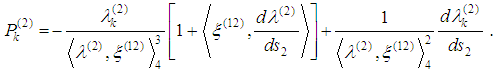 So we obtain eight equations of motion for two-body problem with radiation terms:
So we obtain eight equations of motion for two-body problem with radiation terms: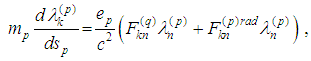
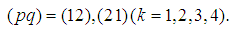 We recall that derivation of the radiation term is based on the physical assumptions from [2].Consider a charge
We recall that derivation of the radiation term is based on the physical assumptions from [2].Consider a charge 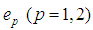 describing any curve
describing any curve 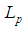 in the space-time. Let
in the space-time. Let 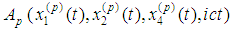 be any event,
be any event, 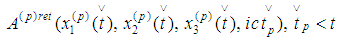 be the intersection of
be the intersection of 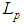 with the null-cone drawn into the past from
with the null-cone drawn into the past from 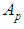 and
and 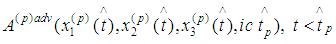 be the intersection of
be the intersection of 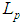 with the null-cone drawn into the future from
with the null-cone drawn into the future from  .The components of the velocity (tangent) vector to the world-line
.The components of the velocity (tangent) vector to the world-line  at
at  are
are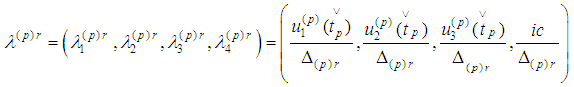 where
where 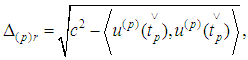 and let
and let 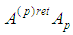 be isotropic vector
be isotropic vector 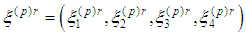 ,where
,where 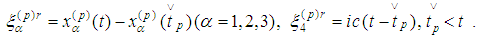 Similarly the components of the velocity (tangent) vector to the world-line
Similarly the components of the velocity (tangent) vector to the world-line 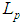 at
at 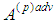 are
are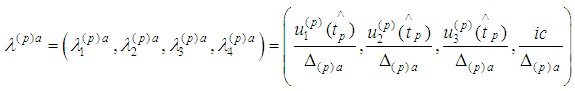 where
where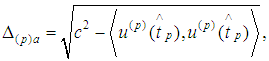 and let
and let 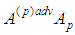 be isotropic vector
be isotropic vector 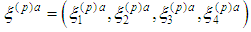 where
where 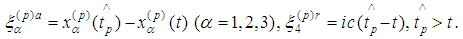 In accordance with Dirac assumptions [2] the radiation term is defined as a half of the difference between both retarded and advanced potentials, that is,
In accordance with Dirac assumptions [2] the radiation term is defined as a half of the difference between both retarded and advanced potentials, that is, 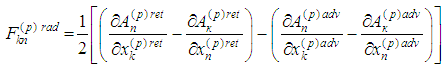 where
where 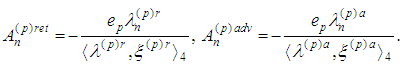 So in view of (3) we obtain the following eight equations:
So in view of (3) we obtain the following eight equations: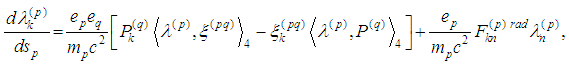 or
or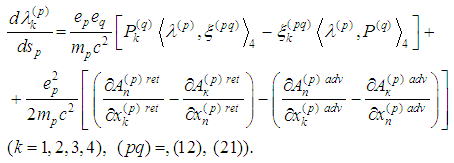 Now follow [33] and [34] we obtain
Now follow [33] and [34] we obtain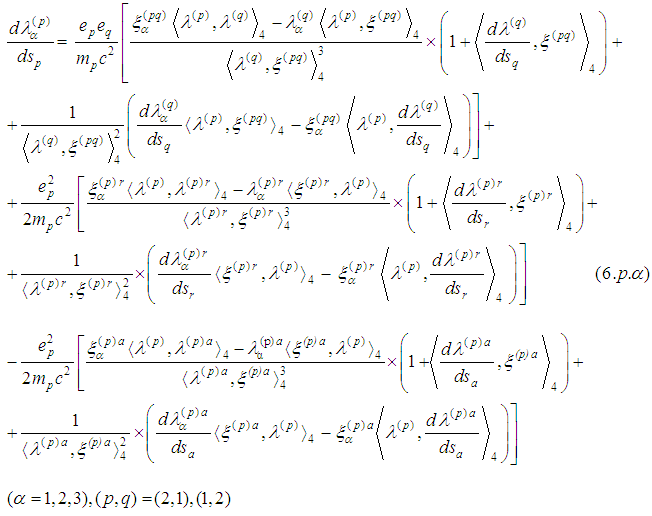
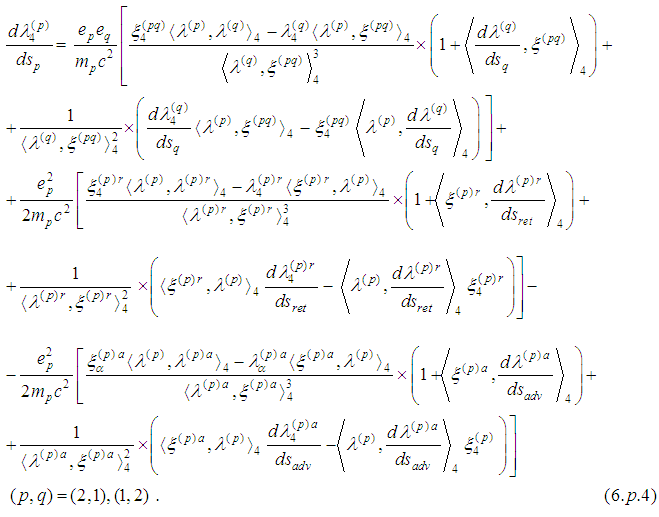
2.2. The Fourth Equation Is a Consequence of the First Three Ones
- The system
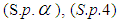 obtained in Supplement 1 can be rewritten as
obtained in Supplement 1 can be rewritten as 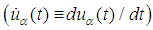

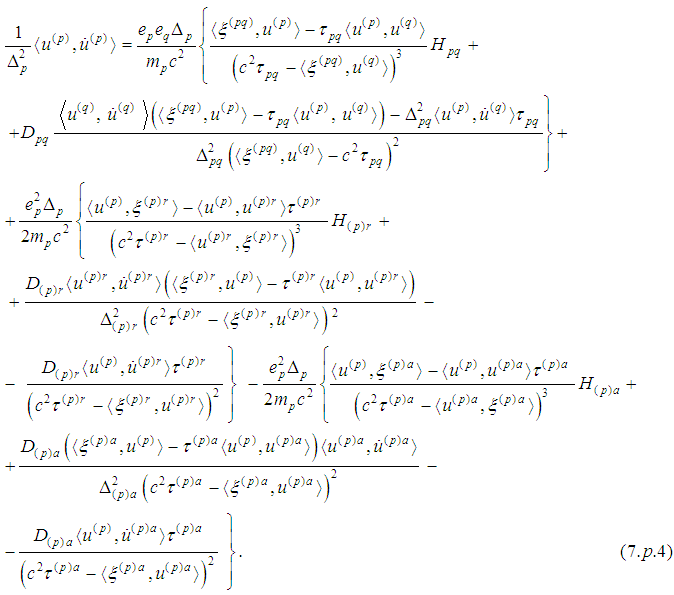 Proceeding as in [30], [34] we multiply
Proceeding as in [30], [34] we multiply 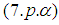 by
by 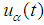 , summing up in α and dividing into c2 we obtain
, summing up in α and dividing into c2 we obtain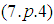 .In other words the fourth equation is a consequence of the first three ones and the eighth equation is a consequence of the previous three ones. In this way we obtain 6 equations for 6 unknown functions.The system from Supplement 2 can be written in the following form
.In other words the fourth equation is a consequence of the first three ones and the eighth equation is a consequence of the previous three ones. In this way we obtain 6 equations for 6 unknown functions.The system from Supplement 2 can be written in the following form 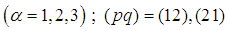 :
: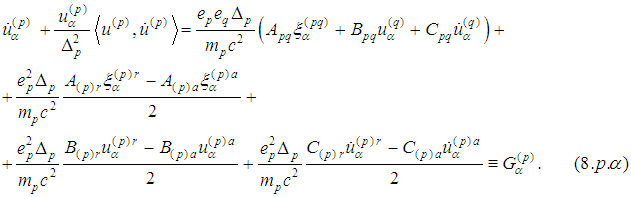 Denoting by
Denoting by 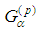 the right-hand sides of
the right-hand sides of 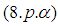 we have to solve the following system with respect to
we have to solve the following system with respect to 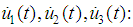
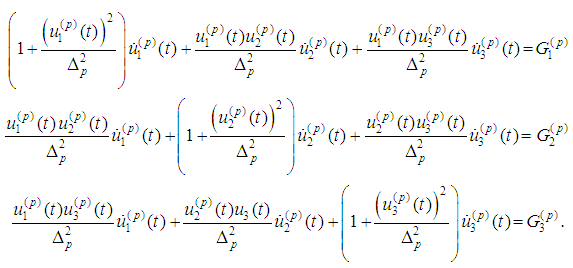 We make the following: Assumption (C): All velocities satisfy the inequalities
We make the following: Assumption (C): All velocities satisfy the inequalities 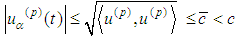 and then
and then 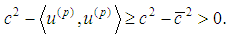 Therefore, the determinant of the above system is
Therefore, the determinant of the above system is 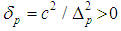 and consequently we reach the system:
and consequently we reach the system: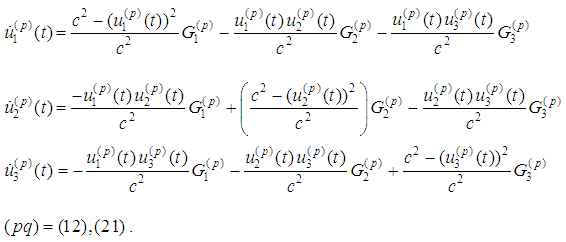 The right-hand side of
The right-hand side of 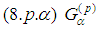 is a sum of two terms
is a sum of two terms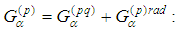 Lorentz term
Lorentz term 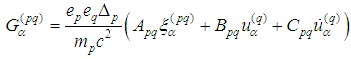 and radiation term
and radiation term 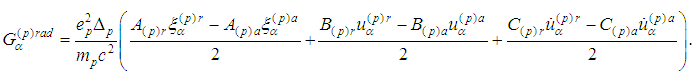
3. Conclusions
- Here we introduce a unified approach to derive two-body problem with radiation terms. The system obtained is of neutral type containing both retarded and advanced arguments. The unknown functions are velocities of the moving particles. The deviating arguments depend on the unknown trajectories. We would like to point that we follow physical reasoning due to Dirac [2] which leads to assumption
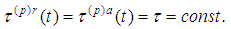 But with accordance of special relativity theory we have to consider radiation time in the form
But with accordance of special relativity theory we have to consider radiation time in the form 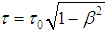 where
where 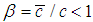 . In view of
. In view of 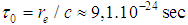 and
and 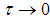 as
as 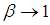 then the parameter
then the parameter 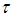 should be consider as an infinitely small parameter. Extending the technique from [30] and [34] we replace the usually accepted second order Dirac’s system of ordinary differential equations by a first order system of neutral equations with both retarded and advanced arguments.We would like to comment our basic assumption (C):
should be consider as an infinitely small parameter. Extending the technique from [30] and [34] we replace the usually accepted second order Dirac’s system of ordinary differential equations by a first order system of neutral equations with both retarded and advanced arguments.We would like to comment our basic assumption (C): 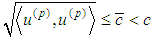 (cf. also [30]). In the Newton theory − the speed of propagation of the interaction is
(cf. also [30]). In the Newton theory − the speed of propagation of the interaction is 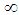 , but anybody cannot reach this speed
, but anybody cannot reach this speed 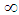 . Here the role of
. Here the role of 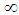 is played by c.Supplement 1In 2.1 we have obtained system
is played by c.Supplement 1In 2.1 we have obtained system 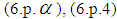 . In order to solve it we have to transform it in a suitable form. First of all we have to find a relation between the relativistic and absolute time. Indeed, following [19], [33], and [34] we assume that
. In order to solve it we have to transform it in a suitable form. First of all we have to find a relation between the relativistic and absolute time. Indeed, following [19], [33], and [34] we assume that 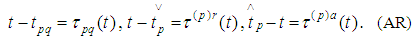 Since
Since 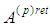 and
and 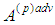 lie on the trajectory
lie on the trajectory  we put
we put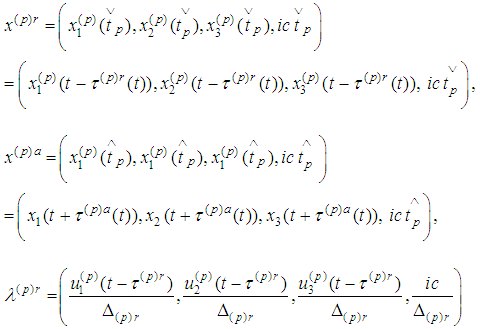 where
where 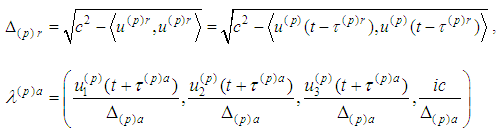 where
where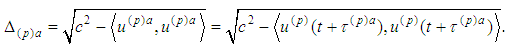
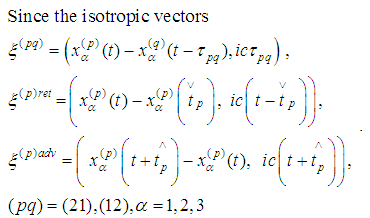 have lengths 0 we obtain
have lengths 0 we obtain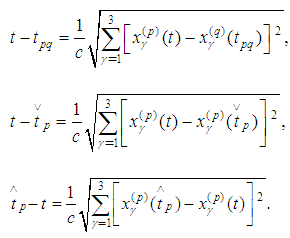 We put
We put 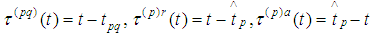 and then
and then 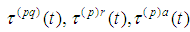 ,can be obtained as solutions of the equations
,can be obtained as solutions of the equations 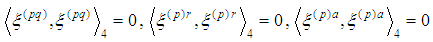 or
or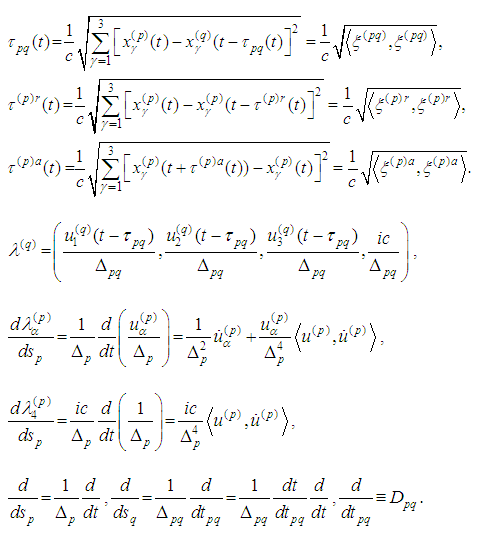 We have to find relations between the derivatives at past, present and future instants. Indeed, extending reasoning from [19], differentiating the relations
We have to find relations between the derivatives at past, present and future instants. Indeed, extending reasoning from [19], differentiating the relations 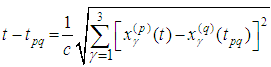 and solving with respect to
and solving with respect to 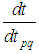 we obtain
we obtain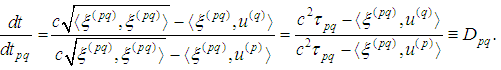 Therefore
Therefore In a similar way we differentiate
In a similar way we differentiate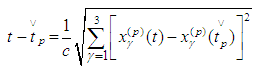 with respect to
with respect to 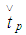 (considering
(considering 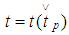 ) and obtain
) and obtain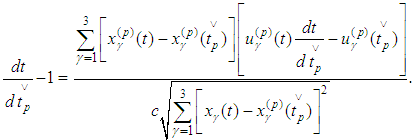 Hence
Hence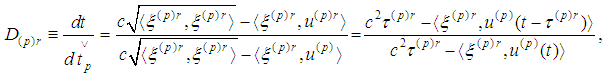 and similarly
and similarly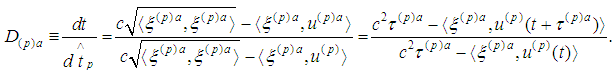 Further on we have
Further on we have
 Substituting the expressions obtained we reach the system
Substituting the expressions obtained we reach the system


 The last equation should be divided into
The last equation should be divided into  . Supplement 2Introduce denotations
. Supplement 2Introduce denotations 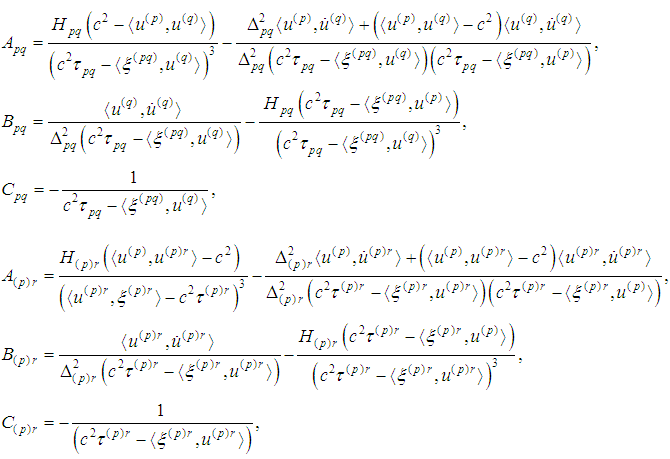
 Regrouping the terms in the right-hand sides of
Regrouping the terms in the right-hand sides of 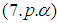 we obtain the system in a vector form:
we obtain the system in a vector form:
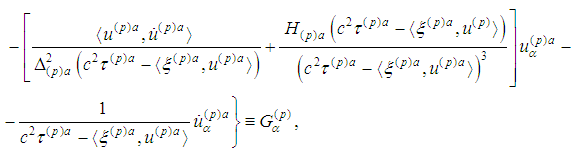

ACKNOWLEDGEMENTS
- The author thanks very much the referee for his very useful suggestions which improve the paper.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML