Yuchuan Wei1, 2
1International Center of Quantum Mechanics, Three Gorges University, China
2Department of Radiation Oncology, Wake Forest University, NC
Correspondence to: Yuchuan Wei, International Center of Quantum Mechanics, Three Gorges University, China.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
There has been a continuous argument on the correctness of the Laskin’s solution for the infinite square well problem in the fractional quantum mechanics. In this paper, we prove that the Laskin’s functions are not amathematical solution to the fractional Schrödinger equation and the equation does not have any nonzero solutions at all in the sense of mathematics. As in the standard quantum mechanics, we view the infinite square well problem as the limit of the finite well problem, and define the solution for the infinite square well problem as the limit of the solution for the finite square well problem. Using the simple property of the infinite operators, we show that Laskin’s function can be the limit solution for the infinite square well problem. The single-sided well problem and the 3 dimensional well problem are included. This operator method works for the same problems in the relativistic quantum mechanicsas well.
Keywords:
Fractional quantum mechanics, Relativistic quantum mechanics, Fractional Schrödinger equation, Relativistic Schrödinger equation
Cite this paper: Yuchuan Wei, The Infinite Square Well Problem in the Standard, Fractional, and Relativistic Quantum Mechanics, International Journal of Theoretical and Mathematical Physics, Vol. 5 No. 4, 2015, pp. 58-65. doi: 10.5923/j.ijtmp.20150504.02.
1. Introduction
In 2000, Laskin introduced the fractional quantum mechanics [1-3]. As an example he solved the infinite square well problem in a piecewise fashion [3]. However, in 2010 Jeng, et al [4] criticized that it was meaningless to solve a nonlocal equation in a piecewise fashion and they demonstrated that it was impossible for the ground state function to satisfy the fractional Schrödinger equation near the boundary inside the well. In a series of papers [5-8], Bayin insisted that he explicitly completed the calculation in Jeng’s paper and the wave functions did satisfy the fractional Schrödinger equation inside the well. Hawkins and Schwarz [9] claimed that the Bayin’s calculation contained serious mistakes. Luchko [10] provided some evidence that the solution did not satisfy the equation outside the well. On the other hand, Dong [11] re-obtained the Laskin’s solution by solving the fractional Schrödinger equation with the path integral method. It is not easy for readers to judge their mathematical argument [12, 13], but weagree with Jeng’s opinion, including that the piecewise way to solve the equation is wrong, and that the solution does not satisfy the fractional Schrödinger equation, since we will inarguably show that the Laskin’s functions do not satisfy the fractional Schrödinger equation 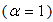 anywhere on the x-axis. However, in fact, this solution does not satisfy the standard Schrödinger equation either, and it is nothing but the limit of the solution to the finite square problem. Without a mathematical definition of the eigenvalues and eigenfunctions of a Hamiltonian operator with local infinity, the argument will be endless. Therefore, in this paper we mathematically define the infinite square well problem as a limit of the finite well. This viewpoint is also useful for other potentials with infinity, such as the coulomb potential in the hydrogen atom, the single-sided harmonic oscillator, etc.Since it is difficult to solve the fractional Schrödinger’s equation with a finite square well potential, we wish a direct way to find the solution of the infinite square well problem. Fortunately, we can express the fractional Hamiltonian in terms of the standard Hamiltonian. In the same way, we can also solve the infinite square well problem in the relativistic quantum mechanics, since the fractional and relativistic quantum mechanics are closely related. We acknowledge that these solutions need to be verified when the solutions to the finite square well problem are reported later. We first recall the infinite square well problem in standard quantum mechanics, and then solve the problem in the fractional quantum mechanics and in the relativistic quantum mechanics.
anywhere on the x-axis. However, in fact, this solution does not satisfy the standard Schrödinger equation either, and it is nothing but the limit of the solution to the finite square problem. Without a mathematical definition of the eigenvalues and eigenfunctions of a Hamiltonian operator with local infinity, the argument will be endless. Therefore, in this paper we mathematically define the infinite square well problem as a limit of the finite well. This viewpoint is also useful for other potentials with infinity, such as the coulomb potential in the hydrogen atom, the single-sided harmonic oscillator, etc.Since it is difficult to solve the fractional Schrödinger’s equation with a finite square well potential, we wish a direct way to find the solution of the infinite square well problem. Fortunately, we can express the fractional Hamiltonian in terms of the standard Hamiltonian. In the same way, we can also solve the infinite square well problem in the relativistic quantum mechanics, since the fractional and relativistic quantum mechanics are closely related. We acknowledge that these solutions need to be verified when the solutions to the finite square well problem are reported later. We first recall the infinite square well problem in standard quantum mechanics, and then solve the problem in the fractional quantum mechanics and in the relativistic quantum mechanics.
2. Definition of the Infinite Well Problem
In this section we will recallthe relation between the finite and infinite square well problems in the standard quantum mechanics, and accordingly define the infinite square well problem in the fractional quantum mechanics.
2.1. The Finite and Infinite Potential Wells in the Standard Quantum Mechanics
In the standard quantum mechanics [14], the one dimensional time-independent Schrödinger equationis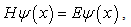 | (1) |
where 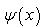 is a wave function defined on the x-axis, and E is an energy. The Hamiltonian operator
is a wave function defined on the x-axis, and E is an energy. The Hamiltonian operator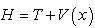 | (2) |
is the summation of the kinetic energy and the potentialenergy of a particle. The standard kinetic energy operator is 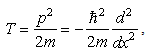 | (3) |
where p is the one dimensional momentum operator 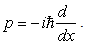 | (4) |
As usual, m is the mass of the particle and 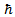 is the reduced Plank constant.A finite square well [15] is defined as
is the reduced Plank constant.A finite square well [15] is defined as 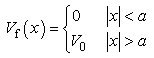 | (5) |
where 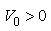 is the depth of the well and 2a is the width of the well. The subscript f means the finite square well. The eigenequation of the finite square well problem is
is the depth of the well and 2a is the width of the well. The subscript f means the finite square well. The eigenequation of the finite square well problem is 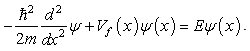 | (6) |
This equation can be solved separately in three regions first and then the piecewise solutions are connected by the continuity condition that the wave function and its derivative must be continuous. This process generates the eigenvalues 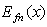 and eigenstates
and eigenstates 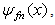 with
with  The state with n=1 is the ground state [15]. One can easily verify that the explicit solutions satisfy the eigenequation at every point on the whole x-axis
The state with n=1 is the ground state [15]. One can easily verify that the explicit solutions satisfy the eigenequation at every point on the whole x-axis | (7) |
which convinces us that the continuity condition we use is suitable. In fact this continuity condition comes from the Schrödinger equation. The infinite square well potential is defined as  | (8) |
At 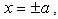 the potential has two infinite jumps. The subscript imeans the infinite square well.Obviously the potential
the potential has two infinite jumps. The subscript imeans the infinite square well.Obviously the potential 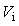 is not real in physics and not well-defined in mathematics, since we do not know how to determine the value of the multiplication
is not real in physics and not well-defined in mathematics, since we do not know how to determine the value of the multiplication 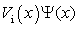 outside the well, even if the wave function outside the well is zero. (Does
outside the well, even if the wave function outside the well is zero. (Does 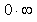 equal
equal 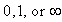 ?) In physics this potential is used as a simplified model for ‘a very deep finite square well’. Conventionally the Schrödinger equation
?) In physics this potential is used as a simplified model for ‘a very deep finite square well’. Conventionally the Schrödinger equation 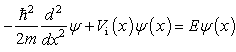 | (9) |
is solved in a piecewise way again [15]. The wave function outside the well is zero because the potential is infinite and the wavefunction inside the well is a sine or cosine function. The revised continuity condition for this case is that the wave functions must be continuous but their derivative should not be. The infinite square well problem has the simple and well-known solution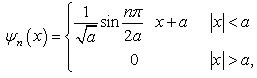 | (10) |
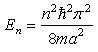 | (11) |
for 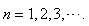 However, we emphasize that this solution does not satisfy the Schrödinger Equations (9). Take the ground state as an example, we have
However, we emphasize that this solution does not satisfy the Schrödinger Equations (9). Take the ground state as an example, we have 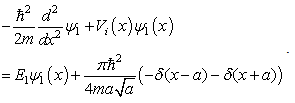 | (12) |
The wave function satisfies the Schrödinger equation everywhere except at x=a and x=-a. This is not a small flaw for a differential equation, and we have to say that the wave functions in (10) are not the solution of the Schrödinger equation at all. The extra terms in the above equation comes from the discontinuity of the derivative of the wave function, but if we keep the derivative of the wavefunction continuous, we can only get a trivial solution 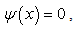 which is meaningless in physics. We have to say that the Schrödinger equation with the infinite square well potential does not have solutions in mathematics. (See the appendix if one feels surprised.)Since the infinite square well is a limit of the finite square well, conventionally we call the limit of the solutions of the finite square well problem
which is meaningless in physics. We have to say that the Schrödinger equation with the infinite square well potential does not have solutions in mathematics. (See the appendix if one feels surprised.)Since the infinite square well is a limit of the finite square well, conventionally we call the limit of the solutions of the finite square well problem 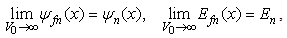 | (13) |
the solution of the infinite square well, and symbolically write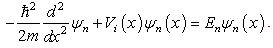 | (14) |
The piecewise way to solve the Schrödinger equation for the infinite square well, together with the aforementioned revised continuity condition, is nothing but an easy and direct way to get the limit of the finite square well solution without solving the finite square well problem. This definition for the infinity potential is applicable for several important cases in quantum mechanics. It helps us to answer the following questions:(1) in what sense the wave functions of the hydrogen atom [14]can satisfy the Schrödinger equation at the origin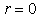 where the coulomb potential
where the coulomb potential 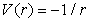 is undefined. (r is the distance of a point to the origin.) (2) why the wave functions for the potential
is undefined. (r is the distance of a point to the origin.) (2) why the wave functions for the potential 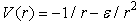 [14], where
[14], where 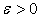 is much smaller than 1, can be divergent at the origin while we claim that the wave functions should be be continuous and differentiable everyday, (3) why only the odd (rather than even) eigen-functions of the simple harmonic oscillator [15] are the solutions of the single-sided oscillator
is much smaller than 1, can be divergent at the origin while we claim that the wave functions should be be continuous and differentiable everyday, (3) why only the odd (rather than even) eigen-functions of the simple harmonic oscillator [15] are the solutions of the single-sided oscillator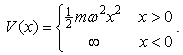 | (15) |
(4) why half-sine functions are the solution of the single-sided infinite square well (or infinite wall) but half-cosine functions are not. We will explain this case further in the section III. In one word, the different continuity conditions of wave functions in quantum mechanics are used in order that one can directly find the limit solution for a potential with infinity, instead of solving the Schrödinger equation with a corresponding finite potential first and then calculating the limit of the solutions.
2.2. The Laskin’s Solution of the Infinite Square Well
In 2000, Laskin generalized the classical kinetic and momentum relation to 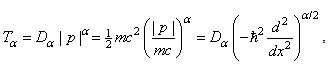 | (16) |
where the coefficient 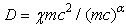 with χ a positive real number, and c is the speed of the light. When
with χ a positive real number, and c is the speed of the light. When 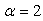 , taking
, taking 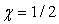 and hence
and hence 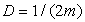 , the fractional kinetic energy recovers the standard kinetic energy, i.e.
, the fractional kinetic energy recovers the standard kinetic energy, i.e. 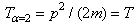 . Originally Laskin [1-3] required the fractional parameter
. Originally Laskin [1-3] required the fractional parameter 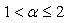 , but in this paper we allow
, but in this paper we allow 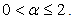 The fractional Schrödinger equation is
The fractional Schrödinger equation is 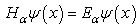 | (17) |
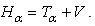 | (18) |
For the infinite square well problem, we have 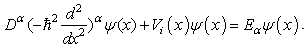 | (19) |
Laskin [3] solved the equation above in a piecewise fashion, and got the same wave functions and a new energy level 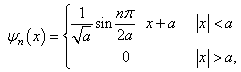 | (20) |
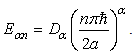 | (21) |
However, in 2010 Jeng, et al [4] criticized that it was meaningless to solve the nonlocal equation (19) in a piecewise fashion and by contradiction they demonstrated that the ground state function did not satisfy the fractional Schrödinger equation.We believe that Jeng et al is correct and Basin is wrongin this argument. There are two reasons. (1) The inarguable evidence is that the solution does not satisfy the fractional Schrödinger equation 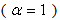 anywhere on the x-axis. Taking the ground state as an example, we have the fact
anywhere on the x-axis. Taking the ground state as an example, we have the fact 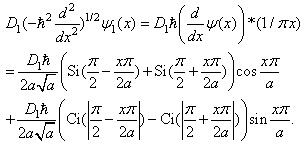 | (22) |
The above function is not proportional to 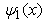 inside the well, it is not zero outside the well, and it is divergent at the boundaries
inside the well, it is not zero outside the well, and it is divergent at the boundaries 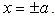 Here Si and Ci are sine and cosine integral functions, respectively. (2) In fact, the fractional Schrödinger equation with the infinite square well (19) does not have any nonzero solutions. Since the potential
Here Si and Ci are sine and cosine integral functions, respectively. (2) In fact, the fractional Schrödinger equation with the infinite square well (19) does not have any nonzero solutions. Since the potential 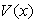 is infinity, to avoid
is infinity, to avoid 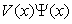 be infinity, we have to let
be infinity, we have to let 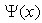 be zero outside the well, that is,
be zero outside the well, that is, 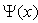 is a compactly supported function. Thuswe have
is a compactly supported function. Thuswe have 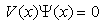 on the x-axis (if we take
on the x-axis (if we take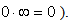 For
For 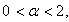 the kinetic energy operator is nonlocal, so the resultant function
the kinetic energy operator is nonlocal, so the resultant function 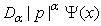 will be extended outside the well. Therefore Equation (19) requires a compacted function to equal a non-compacted function. This is impossible. Therefore there are no nonzero solutions to the fractional Schrödinger equation
will be extended outside the well. Therefore Equation (19) requires a compacted function to equal a non-compacted function. This is impossible. Therefore there are no nonzero solutions to the fractional Schrödinger equation 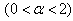 with an infinite square well potential. By the way, Luchko [10] ever had a conjecture that the solution for the infinite square well problem in fractional quantum mechanics should be treated as a new special function.Now let us define the infinite square well problem and its solutionin the fractional quantum mechanics mathematically. Definition 1. The solution of the infinite square well problem.Suppose the fractional Schrödinger equation for the finite square well potential
with an infinite square well potential. By the way, Luchko [10] ever had a conjecture that the solution for the infinite square well problem in fractional quantum mechanics should be treated as a new special function.Now let us define the infinite square well problem and its solutionin the fractional quantum mechanics mathematically. Definition 1. The solution of the infinite square well problem.Suppose the fractional Schrödinger equation for the finite square well potential 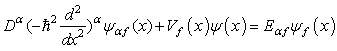 has the solutions
has the solutions 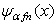 and
and 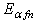 with
with 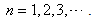 If their limits exist
If their limits exist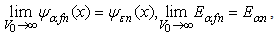 | (23) |
we say that they are the solutions for the infinite square well problem, and symbolically write 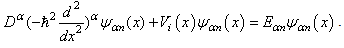 Obviously it will be difficult and complicated to solve the infinite square well problem according to the above definition. Before any strict solutions have been reported in the publications, let us develop a tentative way to solve the infinite square well problem based on some intuitive property of the infinity operator.
Obviously it will be difficult and complicated to solve the infinite square well problem according to the above definition. Before any strict solutions have been reported in the publications, let us develop a tentative way to solve the infinite square well problem based on some intuitive property of the infinity operator.
3. The Infinite Square Well Problems in Fractional Quantum Mechanics
Based on the relation between the standard and fractional Hamiltonians, one can construct a non-piecewise method for the infinite square well. There are three cases, (1) one dimensional, (2) three dimensional and (3) one-sided infinite square well problems.
3.1. The 1D Infinite Square Well Problem
For the 1D infinite square well problem, the fractional Hamiltonian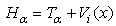 | (24) |
can be expressed in terms of the standard Hamiltonian 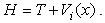 | (25) |
as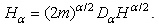 | (26) |
Here is the deduction of the above operator relationship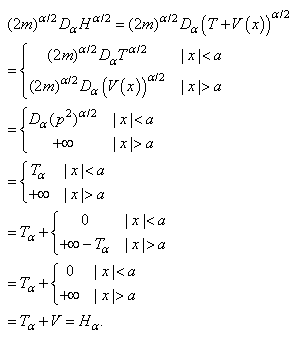 | (27) |
Therefore we have 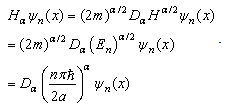 | (28) |
We see that the wave functions of the fractional Hamiltonian are the same functions of the original Hamiltonian, and the new energy levels are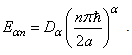 | (29) |
That is to say, the Laskin’s solution is re-obtained in a non-piecewise fashion. In the above deduction, we use some formal operations of the infinity operator 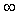 , such as
, such as  | (30) |
3.2. The 3D Infinite Square Well Problem
In quantum mechanics, the 3D infinite square well is defined 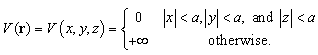 | (31) |
Here 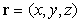 is a point in the 3D Euclidean space. Please notice that the 3D infinite square well potential is the summation of three one dimensional infinite square wells,
is a point in the 3D Euclidean space. Please notice that the 3D infinite square well potential is the summation of three one dimensional infinite square wells, 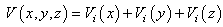 | (32) |
since 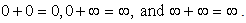 By the way, a 3D finite square well potential does not have such a simple relation, so it is very difficult and complicated to solve. Here we see that the use of the infinity potential
By the way, a 3D finite square well potential does not have such a simple relation, so it is very difficult and complicated to solve. Here we see that the use of the infinity potential 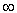 can greatly simplify the problem with a very big finite potential. The standard Hamiltonian is
can greatly simplify the problem with a very big finite potential. The standard Hamiltonian is 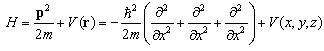 | (33) |
where 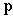 is the 3D momentum operator. The Schrödinger’s equation
is the 3D momentum operator. The Schrödinger’s equation 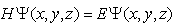 | (34) |
has the solution 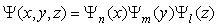 | (35) |
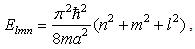 | (36) |
with 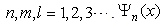 is defined in (10)The fractional Hamilton is
is defined in (10)The fractional Hamilton is 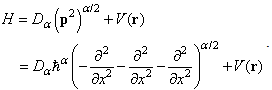 | (37) |
Again, we have the same relation between the standard and fractional Hamiltonian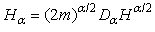 | (38) |
Therefore, the fractional Schrödinger equation 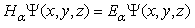 | (39) |
has the solution 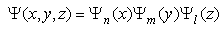 | (40) |
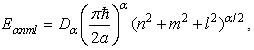 | (41) |
With 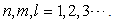
3.3. One-sided Infinite Square Well
The 1D one-sided infinite square well is defined as 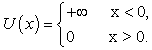 | (42) |
The standard Hamilton is 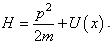 | (43) |
The Schrödinger equation 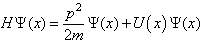 | (44) |
has the solution 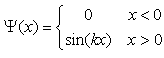 | (45) |
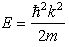 | (46) |
with 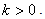 Here we repeat that the wave function in (45) does not satisfy the Schrödinger equation (44) at x=0. Then one natural question is why we do not call
Here we repeat that the wave function in (45) does not satisfy the Schrödinger equation (44) at x=0. Then one natural question is why we do not call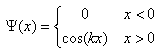 | (47) |
a solution.In fact, for a finite single–sided square well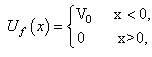 | (48) |
the solution to the Schrödinger equation is 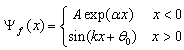 | (49) |
Here the parameters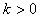 and
and 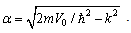 The other parameters A and
The other parameters A and 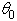 are chosen so that this solution is continuous and differentiable at x=0. It is easy to verify that
are chosen so that this solution is continuous and differentiable at x=0. It is easy to verify that 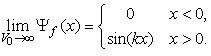 | (50) |
This is the reason why the half-sine function in (45) is a solution, but the half-cosine function 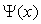 in (47) is not. The fractional Hamiltonian is
in (47) is not. The fractional Hamiltonian is 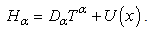 | (51) |
Based on (26), the fractional Schrödinger equation 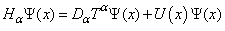 | (52) |
has the solution 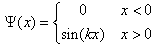 | (53) |
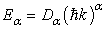 | (54) |
with 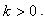
4. Infinite Square Well Problems in Relativistic Quantum Mechanics
According to special relativity [14], the relation between the kinetic energy 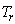 and the 3D momentum
and the 3D momentum 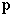 is
is 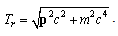 | (55) |
The subscript r means special relativity. The relativistic Hamiltonian [14] is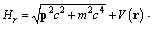 | (56) |
In Summerfield’s quantum theory [14], this Hamiltonian leaded to an energy formula for the coulomb potential, which accurately matches the hydrogen spectrum with the fine structure. Accordingly, the relativistic Schrödinger equation is 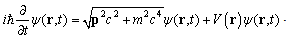 | (57) |
The square root operator above is defined by the Fourier Transformation of the wave function, 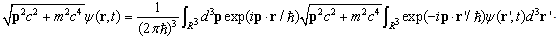 | (58) |
Obviously it is difficult to deal with this equation mathematically [14], so this equation had been abandoned until recently when we discovered that its energy formula has an extremely valuable 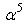 terms, which is 41% of the experimental Lamb shift [16, 17]. As the only exception in this paper, the notation
terms, which is 41% of the experimental Lamb shift [16, 17]. As the only exception in this paper, the notation 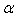 stands for the fine structure constant rather than the fractional order. For a low speed motion, the relativistic equation (57) recovers the Schrödinger equation
stands for the fine structure constant rather than the fractional order. For a low speed motion, the relativistic equation (57) recovers the Schrödinger equation 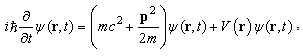 whose fractional parameter
whose fractional parameter 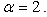 For a very high speed motion, if the rest energy can be neglected approximately, we have
For a very high speed motion, if the rest energy can be neglected approximately, we have 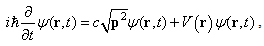 | (59) |
which is the fractional Schrödinger equation with 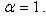 Generally speaking, if the speed of a particle increases from low to high, the relativistic Schrödinger equation (57) will approximately relate to a fractional Schrödinger equation, whose parameters
Generally speaking, if the speed of a particle increases from low to high, the relativistic Schrödinger equation (57) will approximately relate to a fractional Schrödinger equation, whose parameters 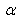 changes from 2 to 1. Therefore the fractional and the relativistic Schrödinger equation should be studied at the same time as two sister equations.
changes from 2 to 1. Therefore the fractional and the relativistic Schrödinger equation should be studied at the same time as two sister equations.
4.1. The 1D Infinite Square Well
For the one-dimensional infinite square well problem, the relativistic Hamiltonian is 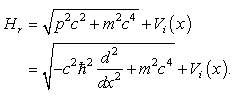 | (60) |
Again, we can express the relativistic Hamiltonian in terms of the classical Hamiltonian as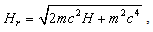 | (61) |
since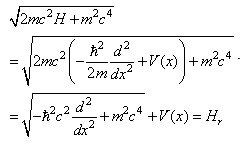 | (62) |
See the stepwise deduction in (27) for details.Therefore the Laskin’s wave functions 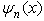 satisfy the relativistic Schrödinger equation
satisfy the relativistic Schrödinger equation 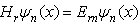 | (63) |
with a new energy level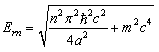 | (64) |
for 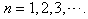 For the extreme relativistic case, we have
For the extreme relativistic case, we have 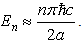 | (65) |
4.2. The 3D Infinite Square Well Problem
The relativistic Hamiltonian 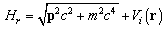 | (66) |
can be expressed in terms of the classical Hamiltonian 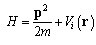 as
as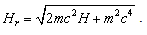 | (67) |
Therefore, the relativistic Schrödinger equation 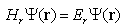 | (68) |
has the solution 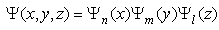 | (69) |
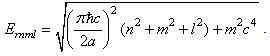 | (70) |
4.3. The One-sided Infinite Square Well Problem
The relativistic Hamiltonian for the one-sided square well is 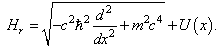 | (71) |
Based on the relation between the relativistic standard Hamiltonians (61), we know that the relativistic Schrödinger equation has the solution 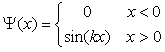 | (72) |
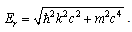 | (73) |
5. Conclusions
We agree with Jeng et al that the fractional Schrödinger equation cannot be solved in a piecewise fashion, and the Laskin’s functions are not a mathematical solution of this equation. On the other hand, since these functions are not the mathematical solution of the standard Schrödinger equation either and are just the limit of the solutions of the finite square well, to disprove the Laskin’s solution, one needs to solve the finite square well problem and take the limit of the solutions. Before the solution of the finite square well problem is reported, we develop a tentative direct method to solve the infinite square well problem in three cases using the straightforward property of the infinity operator. Meanwhile, we point out that the relativistic quantum mechanics is an approximate realization of the fractional quantum mechanics and the infinite square well problem can be treated in a same way.Note 1. We just noticed that the paper [18] reported some initial research on the one dimensional relativistic infinite square well, but to utilize the existing mathematical results, they used a completely different definition on the infinite square well, which had no relation to the finite square well. They defined 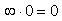 in the multiplication
in the multiplication 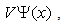 and artificially demanded the resultant function of the Hamiltonian operator to become zerooutside the well though they are actually not. From the viewpoint of physics, they changed the infinite square well problem to another one. Note 2. In [4], there were two sentences that “By raising that Hamiltonian to the power α/2, we get a plausible fractional Laplacian and Eq. (7) is indeed a solution. However, this is not the Riesz fractional derivative.” These words remind us that Jeng et al knew the method used in this paper but thought it did not work since the operator in this method was not Riesz fractional derivative. In fact, this is the Riesz fractional derivative, see Equation (7) in [1] for the definition.
and artificially demanded the resultant function of the Hamiltonian operator to become zerooutside the well though they are actually not. From the viewpoint of physics, they changed the infinite square well problem to another one. Note 2. In [4], there were two sentences that “By raising that Hamiltonian to the power α/2, we get a plausible fractional Laplacian and Eq. (7) is indeed a solution. However, this is not the Riesz fractional derivative.” These words remind us that Jeng et al knew the method used in this paper but thought it did not work since the operator in this method was not Riesz fractional derivative. In fact, this is the Riesz fractional derivative, see Equation (7) in [1] for the definition.
ACKNOWLEDGEMENTS
This work is supported by the National Natural Science Foundation. The research on the relativistic Schrödinger equation was supported by Gansu Industry University during 1989-1991, with a subject title ‘On the solvability of an equation with a square root operator in relativistic quantum mechanics’. Thanks for the support from my family as well.
Appendix 1. ‘Particle in a box’
Usually in quantum mechanics it is also demanded that the derivative of the wavefunction in addition to the wavefunction itself be continuous; here this demand would lead to the only solution being the constant zero function, which is not what we desire, so we give up this demand (as this system with infinite potential can be regarded as a nonphysical abstract limiting case, we can treat it as such and "bend the rules"). Note that giving up this demand means that the wavefunction is not a differentiable function at the boundary of the box, and thus it can be said that the wavefunction does not solve the Schrödinger equation at the boundary points x = 0 and x = L (but does solve everywhere else).http://en.wikipedia.org/wiki/Particle_in_a_box
Appendix 2. An Alternative Definition on the Infinite Square Well Problem
Definition 2. The solution of the infinite square well problem.We define a potential 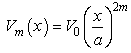 with
with 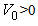 and a>0, m=1,2,3.Suppose the fractional Schrödinger equation for the finite potential
and a>0, m=1,2,3.Suppose the fractional Schrödinger equation for the finite potential 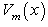
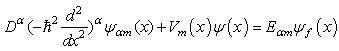 has the solutions
has the solutions 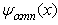 and
and 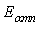 with
with 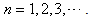 If their limits exist
If their limits exist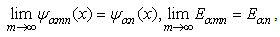 we say that they are the solutions for the infinite square well problem, and symbolically write
we say that they are the solutions for the infinite square well problem, and symbolically write 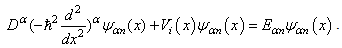
References
| [1] | N. Laskin, “Fractional quantum mechanics,” Physical Review E 62, pp3135-3145 (2000). |
| [2] | N. Laskin, “Fractional Schrödinger equation,” Physical Review E66, 056108 (2002). |
| [3] | N. Laskin, “Fractional and quantum mechanics,” Chaos 10, pp780-790 (2000). |
| [4] | M. Jeng, S.-L.-Y. Xu, E. Hawkins, and J. M. Schwarz, “On the nonlocality of the fractional Schrödinger equation,” Journal of Mathematical Physics 51, 062102 (2010). |
| [5] | S. S. Bayin, “On the consistency of the solutions of the space fractional Schrödinger equation,” J. Math.Phys. 53, 042105 (2012). |
| [6] | S. S. Bayin, “Comment‘On the consistency of the solutions of the space fractional Schrödinger equation,” Journal of Mathematical Physics 53, 084101 (2012). |
| [7] | S. S. Bayin, “Comment‘On the consistency of the solutions of the space fractional Schrödinger equation,” Journal of Mathematical Physics 54, 074101 (2013). |
| [8] | S. S. Bayin, “Consistency problem of the solutions of the space fractional Schrödinger equation”, Journal of Mathematical Physics 54, 092101(2013). |
| [9] | E. Hawkins and J. M. Schwarz, “Comment‘On the consistency of the solutions of the space fractional Schrödinger equation,” Journal of Mathematical Physics 54, 014101 (2013). |
| [10] | Y. Luchko, “Fractional Schrödinger equation for a particle moving in a potential well,” Journal of Mathematical Physics 54, 012111 (2013). |
| [11] | J. Dong, “Levy path integral approach to the solution of the fractional Schrödinger equation with infinite square well,” preprint arXiv:1301.3009v1 [math-ph] (2013). |
| [12] | J. Tare and J. Esguerra, “Bound states for multiple Dirac-δ wells in space-fractional quantum mechanics,” Journal of Mathematical Physics 55, 012106 (2014). |
| [13] | J. Tare and J. Esguerra, “Transmission through locally periodic potentials in space-fractional quantum mechanics,” Physica A: Statistical Mechanics and its Applications 407(2014), pp 43–53. |
| [14] | A. Messiah, Quantum Mechanics Vol 1, 2(North Holland Publishing Company 1965). |
| [15] | M. Bellonia and R.W. Robinettb, “The infinite well and Dirac delta function potentials aspedagogical, mathematical and physical models inquantum mechanics,” Physics Reports 540(2014), pp25-122. |
| [16] | Y. Wei, “The Quantum Mechanics Explanation for the Lamb Shift,” SOP Transactions on Theoretical Physics1(2014), no. 4, pp.1-12. |
| [17] | Y. Wei, “On the divergence difficulty in perturbation method for relativistic correction of energy levels of H atom,” College Physics14(1995), No. 9, pp25-29 |
| [18] | K. Kaleta, M. Kwasnicki, and J. Malecki, “One-dimensional quasi-relativistic particle in a box,” Reviews in Mathematical Physics25, No. 8 (2013) 1350014. |
 anywhere on the x-axis. However, in fact, this solution does not satisfy the standard Schrödinger equation either, and it is nothing but the limit of the solution to the finite square problem. Without a mathematical definition of the eigenvalues and eigenfunctions of a Hamiltonian operator with local infinity, the argument will be endless. Therefore, in this paper we mathematically define the infinite square well problem as a limit of the finite well. This viewpoint is also useful for other potentials with infinity, such as the coulomb potential in the hydrogen atom, the single-sided harmonic oscillator, etc.Since it is difficult to solve the fractional Schrödinger’s equation with a finite square well potential, we wish a direct way to find the solution of the infinite square well problem. Fortunately, we can express the fractional Hamiltonian in terms of the standard Hamiltonian. In the same way, we can also solve the infinite square well problem in the relativistic quantum mechanics, since the fractional and relativistic quantum mechanics are closely related. We acknowledge that these solutions need to be verified when the solutions to the finite square well problem are reported later. We first recall the infinite square well problem in standard quantum mechanics, and then solve the problem in the fractional quantum mechanics and in the relativistic quantum mechanics.
anywhere on the x-axis. However, in fact, this solution does not satisfy the standard Schrödinger equation either, and it is nothing but the limit of the solution to the finite square problem. Without a mathematical definition of the eigenvalues and eigenfunctions of a Hamiltonian operator with local infinity, the argument will be endless. Therefore, in this paper we mathematically define the infinite square well problem as a limit of the finite well. This viewpoint is also useful for other potentials with infinity, such as the coulomb potential in the hydrogen atom, the single-sided harmonic oscillator, etc.Since it is difficult to solve the fractional Schrödinger’s equation with a finite square well potential, we wish a direct way to find the solution of the infinite square well problem. Fortunately, we can express the fractional Hamiltonian in terms of the standard Hamiltonian. In the same way, we can also solve the infinite square well problem in the relativistic quantum mechanics, since the fractional and relativistic quantum mechanics are closely related. We acknowledge that these solutions need to be verified when the solutions to the finite square well problem are reported later. We first recall the infinite square well problem in standard quantum mechanics, and then solve the problem in the fractional quantum mechanics and in the relativistic quantum mechanics. 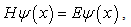
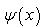 is a wave function defined on the x-axis, and E is an energy. The Hamiltonian operator
is a wave function defined on the x-axis, and E is an energy. The Hamiltonian operator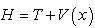
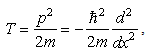
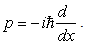
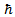 is the reduced Plank constant.A finite square well [15] is defined as
is the reduced Plank constant.A finite square well [15] is defined as 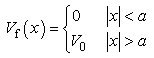
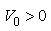 is the depth of the well and 2a is the width of the well. The subscript f means the finite square well. The eigenequation of the finite square well problem is
is the depth of the well and 2a is the width of the well. The subscript f means the finite square well. The eigenequation of the finite square well problem is 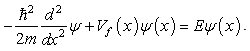
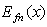 and eigenstates
and eigenstates 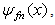 with
with 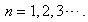 The state with n=1 is the ground state [15]. One can easily verify that the explicit solutions satisfy the eigenequation at every point on the whole x-axis
The state with n=1 is the ground state [15]. One can easily verify that the explicit solutions satisfy the eigenequation at every point on the whole x-axis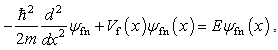
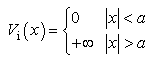
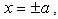 the potential has two infinite jumps. The subscript imeans the infinite square well.Obviously the potential
the potential has two infinite jumps. The subscript imeans the infinite square well.Obviously the potential 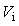 is not real in physics and not well-defined in mathematics, since we do not know how to determine the value of the multiplication
is not real in physics and not well-defined in mathematics, since we do not know how to determine the value of the multiplication 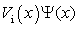 outside the well, even if the wave function outside the well is zero. (Does
outside the well, even if the wave function outside the well is zero. (Does 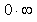 equal
equal 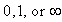 ?) In physics this potential is used as a simplified model for ‘a very deep finite square well’. Conventionally the Schrödinger equation
?) In physics this potential is used as a simplified model for ‘a very deep finite square well’. Conventionally the Schrödinger equation 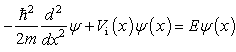
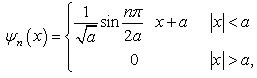
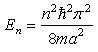
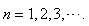 However, we emphasize that this solution does not satisfy the Schrödinger Equations (9). Take the ground state as an example, we have
However, we emphasize that this solution does not satisfy the Schrödinger Equations (9). Take the ground state as an example, we have 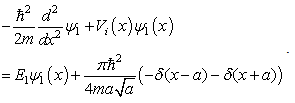
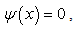 which is meaningless in physics. We have to say that the Schrödinger equation with the infinite square well potential does not have solutions in mathematics. (See the appendix if one feels surprised.)Since the infinite square well is a limit of the finite square well, conventionally we call the limit of the solutions of the finite square well problem
which is meaningless in physics. We have to say that the Schrödinger equation with the infinite square well potential does not have solutions in mathematics. (See the appendix if one feels surprised.)Since the infinite square well is a limit of the finite square well, conventionally we call the limit of the solutions of the finite square well problem 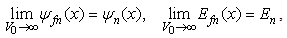
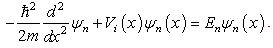
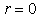 where the coulomb potential
where the coulomb potential 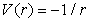 is undefined. (r is the distance of a point to the origin.) (2) why the wave functions for the potential
is undefined. (r is the distance of a point to the origin.) (2) why the wave functions for the potential 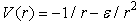 [14], where
[14], where 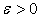 is much smaller than 1, can be divergent at the origin while we claim that the wave functions should be be continuous and differentiable everyday, (3) why only the odd (rather than even) eigen-functions of the simple harmonic oscillator [15] are the solutions of the single-sided oscillator
is much smaller than 1, can be divergent at the origin while we claim that the wave functions should be be continuous and differentiable everyday, (3) why only the odd (rather than even) eigen-functions of the simple harmonic oscillator [15] are the solutions of the single-sided oscillator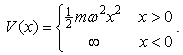
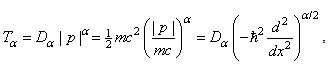
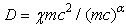 with χ a positive real number, and c is the speed of the light. When
with χ a positive real number, and c is the speed of the light. When 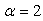 , taking
, taking 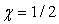 and hence
and hence 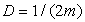 , the fractional kinetic energy recovers the standard kinetic energy, i.e.
, the fractional kinetic energy recovers the standard kinetic energy, i.e. 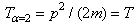 . Originally Laskin [1-3] required the fractional parameter
. Originally Laskin [1-3] required the fractional parameter 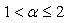 , but in this paper we allow
, but in this paper we allow 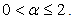 The fractional Schrödinger equation is
The fractional Schrödinger equation is 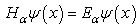
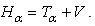
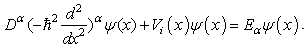
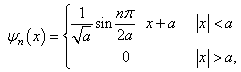
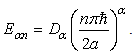
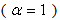 anywhere on the x-axis. Taking the ground state as an example, we have the fact
anywhere on the x-axis. Taking the ground state as an example, we have the fact 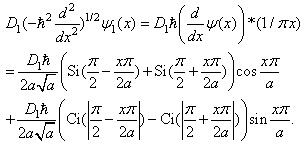
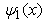 inside the well, it is not zero outside the well, and it is divergent at the boundaries
inside the well, it is not zero outside the well, and it is divergent at the boundaries 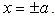 Here Si and Ci are sine and cosine integral functions, respectively. (2) In fact, the fractional Schrödinger equation with the infinite square well (19) does not have any nonzero solutions. Since the potential
Here Si and Ci are sine and cosine integral functions, respectively. (2) In fact, the fractional Schrödinger equation with the infinite square well (19) does not have any nonzero solutions. Since the potential 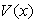 is infinity, to avoid
is infinity, to avoid 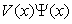 be infinity, we have to let
be infinity, we have to let 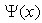 be zero outside the well, that is,
be zero outside the well, that is, 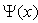 is a compactly supported function. Thuswe have
is a compactly supported function. Thuswe have 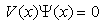 on the x-axis (if we take
on the x-axis (if we take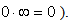 For
For 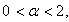 the kinetic energy operator is nonlocal, so the resultant function
the kinetic energy operator is nonlocal, so the resultant function 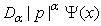 will be extended outside the well. Therefore Equation (19) requires a compacted function to equal a non-compacted function. This is impossible. Therefore there are no nonzero solutions to the fractional Schrödinger equation
will be extended outside the well. Therefore Equation (19) requires a compacted function to equal a non-compacted function. This is impossible. Therefore there are no nonzero solutions to the fractional Schrödinger equation 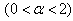 with an infinite square well potential. By the way, Luchko [10] ever had a conjecture that the solution for the infinite square well problem in fractional quantum mechanics should be treated as a new special function.Now let us define the infinite square well problem and its solutionin the fractional quantum mechanics mathematically. Definition 1. The solution of the infinite square well problem.Suppose the fractional Schrödinger equation for the finite square well potential
with an infinite square well potential. By the way, Luchko [10] ever had a conjecture that the solution for the infinite square well problem in fractional quantum mechanics should be treated as a new special function.Now let us define the infinite square well problem and its solutionin the fractional quantum mechanics mathematically. Definition 1. The solution of the infinite square well problem.Suppose the fractional Schrödinger equation for the finite square well potential 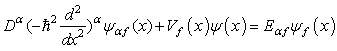 has the solutions
has the solutions 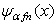 and
and 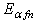 with
with 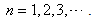 If their limits exist
If their limits exist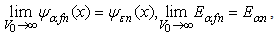
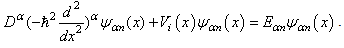 Obviously it will be difficult and complicated to solve the infinite square well problem according to the above definition. Before any strict solutions have been reported in the publications, let us develop a tentative way to solve the infinite square well problem based on some intuitive property of the infinity operator.
Obviously it will be difficult and complicated to solve the infinite square well problem according to the above definition. Before any strict solutions have been reported in the publications, let us develop a tentative way to solve the infinite square well problem based on some intuitive property of the infinity operator. 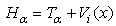
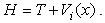
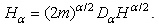
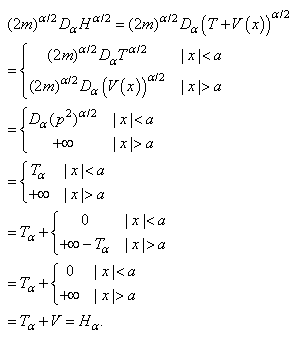
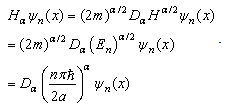
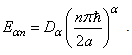
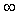 , such as
, such as 
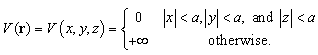
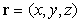 is a point in the 3D Euclidean space. Please notice that the 3D infinite square well potential is the summation of three one dimensional infinite square wells,
is a point in the 3D Euclidean space. Please notice that the 3D infinite square well potential is the summation of three one dimensional infinite square wells, 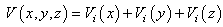
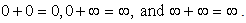 By the way, a 3D finite square well potential does not have such a simple relation, so it is very difficult and complicated to solve. Here we see that the use of the infinity potential
By the way, a 3D finite square well potential does not have such a simple relation, so it is very difficult and complicated to solve. Here we see that the use of the infinity potential 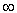 can greatly simplify the problem with a very big finite potential. The standard Hamiltonian is
can greatly simplify the problem with a very big finite potential. The standard Hamiltonian is 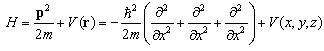
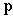 is the 3D momentum operator. The Schrödinger’s equation
is the 3D momentum operator. The Schrödinger’s equation 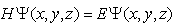
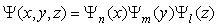
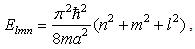
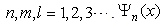 is defined in (10)The fractional Hamilton is
is defined in (10)The fractional Hamilton is 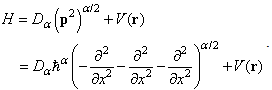
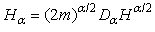
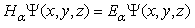
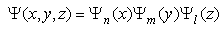
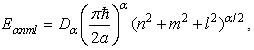
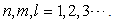
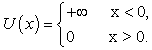
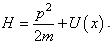
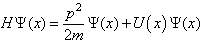
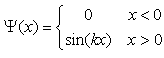
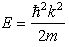
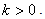 Here we repeat that the wave function in (45) does not satisfy the Schrödinger equation (44) at x=0. Then one natural question is why we do not call
Here we repeat that the wave function in (45) does not satisfy the Schrödinger equation (44) at x=0. Then one natural question is why we do not call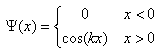
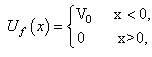
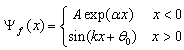
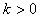 and
and 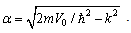 The other parameters A and
The other parameters A and 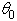 are chosen so that this solution is continuous and differentiable at x=0. It is easy to verify that
are chosen so that this solution is continuous and differentiable at x=0. It is easy to verify that 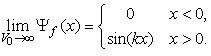
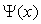 in (47) is not. The fractional Hamiltonian is
in (47) is not. The fractional Hamiltonian is 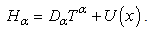
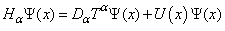
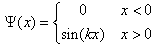
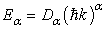
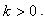
 and the 3D momentum
and the 3D momentum 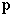 is
is 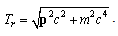
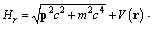
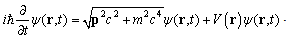
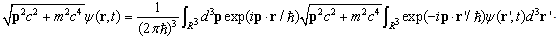
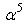 terms, which is 41% of the experimental Lamb shift [16, 17]. As the only exception in this paper, the notation
terms, which is 41% of the experimental Lamb shift [16, 17]. As the only exception in this paper, the notation 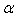 stands for the fine structure constant rather than the fractional order. For a low speed motion, the relativistic equation (57) recovers the Schrödinger equation
stands for the fine structure constant rather than the fractional order. For a low speed motion, the relativistic equation (57) recovers the Schrödinger equation 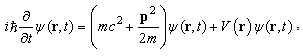 whose fractional parameter
whose fractional parameter 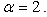 For a very high speed motion, if the rest energy can be neglected approximately, we have
For a very high speed motion, if the rest energy can be neglected approximately, we have 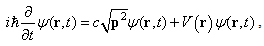
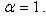 Generally speaking, if the speed of a particle increases from low to high, the relativistic Schrödinger equation (57) will approximately relate to a fractional Schrödinger equation, whose parameters
Generally speaking, if the speed of a particle increases from low to high, the relativistic Schrödinger equation (57) will approximately relate to a fractional Schrödinger equation, whose parameters 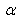 changes from 2 to 1. Therefore the fractional and the relativistic Schrödinger equation should be studied at the same time as two sister equations.
changes from 2 to 1. Therefore the fractional and the relativistic Schrödinger equation should be studied at the same time as two sister equations. 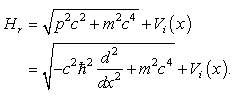
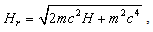
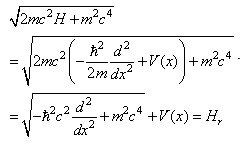
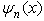 satisfy the relativistic Schrödinger equation
satisfy the relativistic Schrödinger equation 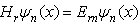
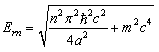
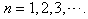 For the extreme relativistic case, we have
For the extreme relativistic case, we have 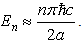
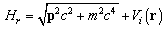
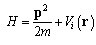 as
as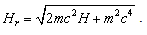
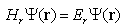
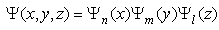
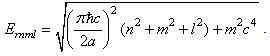
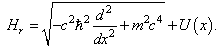
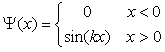
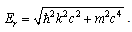
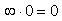 in the multiplication
in the multiplication 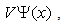 and artificially demanded the resultant function of the Hamiltonian operator to become zerooutside the well though they are actually not. From the viewpoint of physics, they changed the infinite square well problem to another one. Note 2. In [4], there were two sentences that “By raising that Hamiltonian to the power α/2, we get a plausible fractional Laplacian and Eq. (7) is indeed a solution. However, this is not the Riesz fractional derivative.” These words remind us that Jeng et al knew the method used in this paper but thought it did not work since the operator in this method was not Riesz fractional derivative. In fact, this is the Riesz fractional derivative, see Equation (7) in [1] for the definition.
and artificially demanded the resultant function of the Hamiltonian operator to become zerooutside the well though they are actually not. From the viewpoint of physics, they changed the infinite square well problem to another one. Note 2. In [4], there were two sentences that “By raising that Hamiltonian to the power α/2, we get a plausible fractional Laplacian and Eq. (7) is indeed a solution. However, this is not the Riesz fractional derivative.” These words remind us that Jeng et al knew the method used in this paper but thought it did not work since the operator in this method was not Riesz fractional derivative. In fact, this is the Riesz fractional derivative, see Equation (7) in [1] for the definition.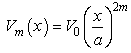 with
with 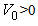 and a>0, m=1,2,3.Suppose the fractional Schrödinger equation for the finite potential
and a>0, m=1,2,3.Suppose the fractional Schrödinger equation for the finite potential 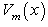
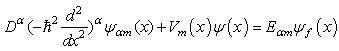 has the solutions
has the solutions 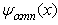 and
and 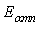 with
with 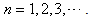 If their limits exist
If their limits exist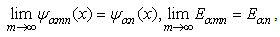 we say that they are the solutions for the infinite square well problem, and symbolically write
we say that they are the solutions for the infinite square well problem, and symbolically write 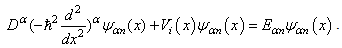
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML