Takaaki Shirahata
Laboratory of Pharmaceutical Education, Kagawa School of Pharmaceutical Sciences, Tokushima Bunri University, Shido, Japan
Correspondence to: Takaaki Shirahata, Laboratory of Pharmaceutical Education, Kagawa School of Pharmaceutical Sciences, Tokushima Bunri University, Shido, Japan.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Harish and Golomb developed a mathematical model of vibrissa motoneurons (vMN), which was described by a system of ordinary differential equations based on the Hodgkin–Huxley formalism. This model can generate repetitive spiking in response to external stimulation. The present study used this model to reveal the relationship between the repetitive spiking and variations in two system parameters of the vMN model: a maximal conductance of a persistent sodium current (gNaP) and a maximal conductance of a transient sodium current (gNa). Numerical analysis by computer simulation clarified the (gNaP, gNa)-parameter space that supported the repetitive spiking.
Keywords:
Hodgkin–Huxley Model, Nonlinear Dynamics, Sodium Conductance, Numerical Simulation
Cite this paper: Takaaki Shirahata, Numerical Study of a Mathematical Model of Vibrissa Motoneurons: The Relationship between Repetitive Spiking and Two Types of Sodium Conductance, International Journal of Theoretical and Mathematical Physics, Vol. 5 No. 3, 2015, pp. 48-52. doi: 10.5923/j.ijtmp.20150503.02.
1. Introduction
Membrane electrical excitability of living cells such as neurons and endocrine cells represents a physical phenomenon that can be analyzed via mathematical models such as the Hodgkin–Huxley model (page 144 in [1]). This model is described by a system of nonlinear ordinary differential equations (ODEs), and its nonlinear dynamics is studied in the field of theoretical and mathematical physics [2]. In addition, physics textbook points out that a detailed analysis of membrane conductance in the Hodgkin–Huxley model is not only interesting but also very important (page 26 in [3]). In fact, analysis of the electrosensory ghostbursting neuron model, which is formulated based on the Hodgkin–Huxley scheme, reveals the relationship between model dynamics and potassium conductance (Figure 13 in [4]). In addition, analysis of the endocrine cell model, which is also formulated based on the Hodgkin–Huxley scheme, reveals the dependence of the model dynamics on two different types of potassium conductance (Figure 3 in [5], Figure 12 in [6], and Figure 4 in [7]). Although analyses of various types of potassium conductance were extensively performed as described above, analysis of sodium conductance, in particular the analysis of the effect of several types of sodium conductance on the neuron model dynamics is limited except for a few studies such as Figure 2 in [8] and Figure 2 in [9]. Therefore, to facilitate further a detailed analysis of membrane conductance, it will be important to analyze sodium conductance in detail.In the present study, we focused on a mathematical model of vibrissa motoneurons (vMN), which plays an important role for vibrissa motor control [10, 11]. This model is also formulated based on the Hodgkin–Huxley scheme and described by a system of nonlinear ODEs (refer to Materials and Methods Section of this paper and Methods Section in [10]). In response to injection of a supra-threshold excitatory current, the vMN model shows repetitive spiking (Figure 2A in [10]). Similar behavior is experimentally observed in the electrophysiological recording (Figure 2 in [12]). Although two types of sodium conductance i.e., persistent sodium conductance and transient sodium conductance are assumed to play an important role in this spiking activity, the influence of variations in these two conductance values on the spiking activity was not clarified in detail in a previous study [10]. Investigation of this influence will provide a deeper understanding of the characteristics of sodium conductance. Therefore, in the present study, computer simulations were carried out to clarify how the repetitive spiking of the vMN model depends on a maximal conductance of persistent sodium current (gNaP) and a maximal conductance of transient sodium current (gNa).
2. Materials and Methods
The vMN model used in the present study is based on the study by Harish and Golomb [10], and it is described by a system of nonlinear ODEs. The model consists of five state variables i.e., a membrane potential of the vMN model [V (mV)] and four gating variables of ionic currents (h, n, u, and r). The time evolution of the five state variables is described as follows: 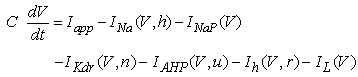 | (1) |

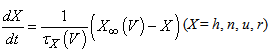
 (2)–(5)where C is the membrane capacitance
(2)–(5)where C is the membrane capacitance 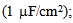 Iapp is the externally injected current of a constant amplitude; INa(V, h), INaP(V), IKdr(V, n), IAHP(V, u), Ih(V, r), and IL(V) denote the transient sodium current, persistent sodium current, delayed rectifier potassium current, calcium-dependent potassium current, hyperpolarization-activated h-current, and leak current, respectively, which are defined below in Equations (6)(11).
Iapp is the externally injected current of a constant amplitude; INa(V, h), INaP(V), IKdr(V, n), IAHP(V, u), Ih(V, r), and IL(V) denote the transient sodium current, persistent sodium current, delayed rectifier potassium current, calcium-dependent potassium current, hyperpolarization-activated h-current, and leak current, respectively, which are defined below in Equations (6)(11). 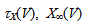 are time constants of activation/ inactivation and steady-state activation/inactivation functions, respectively, which are defined below in Equations (12)(19).
are time constants of activation/ inactivation and steady-state activation/inactivation functions, respectively, which are defined below in Equations (12)(19).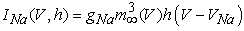 | (6) |
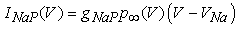 | (7) |
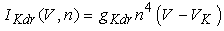 | (8) |
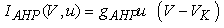 | (9) |
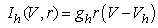 | (10) |
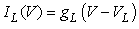 | (11) |
where gNa, gNaP, gKdr, gAHP, gh, and gL are maximal conductances of a transient sodium current (from 0 to 100 mS/cm2), a persistent sodium current (from 0.00 to 0.04 mS/cm2), a delayed rectifier potassium current (20 mS/cm2), a calcium-dependent potassium current (10 mS/cm2), a hyperpolarization-activated h-current (0.05 mS/cm2), and a leak current (0.12 mS/cm2), respectively. VNa, VK, Vh, and VL are reversal potentials of a sodium current (55 mV), a potassium current (−90 mV), a hyperpolarization-activated h-current (−27.4 mV), and a leak current (−70 mV), respectively. m∞(V) and p∞(V) are defined in Equations (20) and (21), respectively.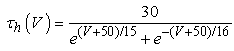 | (12) |
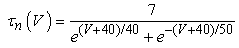 | (13) |
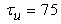 | (14) |
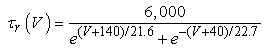 | (15) |
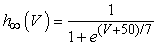 | (16) |
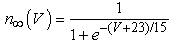 | (17) |
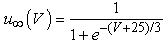 | (18) |
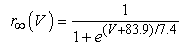 | (19) |
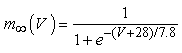 | (20) |
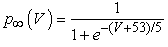 | (21) |
See paper [10] for detailed explanations of the equations. A slow potassium current (M current), an external input current describing noise, and a CPG input current contained in the original model (see Equation (1) in [10]) were not included in Equation (1) of the present study because the spiking activity considered in the present study was observed in the absence of these three currents.The free and open source software Scilab (http://www.scilab.org/) was used to numerically solve the ODEs (initial conditions: V = −65.84 mV, h = 0.92141213, n = 0.0497938, u = 0.00040176, and r = 0.095137881). The detailed information about the vMN model is provided by the ModelDB website: https://senselab.med.yale.edu/ModelDB/ShowModel.cshtml?model=127022.
3. Results
Time courses of the membrane potential of the vMN model at various conditions are illustrated in Figure 1. Figure 1A1 shows the repetitive spiking in response to a weak stimulus (Iapp = 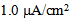 ) injected between 0.2 and 1.8 s. When the value of gNaP was decreased to zero while the other parameter values remained the same as in Figure 1A1, the spiking was completely blocked (Figure 1A2). When the value of gNa was decreased to zero while the other parameter values remained the same as in Figure 1A1, the spiking was also blocked (Figure 1A3). Figure 1B1 shows the repetitive spiking in response to a strong stimulus
) injected between 0.2 and 1.8 s. When the value of gNaP was decreased to zero while the other parameter values remained the same as in Figure 1A1, the spiking was completely blocked (Figure 1A2). When the value of gNa was decreased to zero while the other parameter values remained the same as in Figure 1A1, the spiking was also blocked (Figure 1A3). Figure 1B1 shows the repetitive spiking in response to a strong stimulus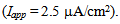 Under this condition, the spiking frequency was greater than that in Figure 1A1. Contrary to Figure 1A2, when the value of gNaP was decreased to zero with the other parameter values remaining the same as in Figure 1B1, the spiking was not blocked, but the spiking frequency decreased compared with that in Figure 1B1 (Figure 1B2). When the value of gNa was decreased to zero with the other parameter values remaining the same as in Figure 1B1, the spiking was completely blocked (Figure 1B3), which was similar to that in Figure 1A3.
Under this condition, the spiking frequency was greater than that in Figure 1A1. Contrary to Figure 1A2, when the value of gNaP was decreased to zero with the other parameter values remaining the same as in Figure 1B1, the spiking was not blocked, but the spiking frequency decreased compared with that in Figure 1B1 (Figure 1B2). When the value of gNa was decreased to zero with the other parameter values remaining the same as in Figure 1B1, the spiking was completely blocked (Figure 1B3), which was similar to that in Figure 1A3.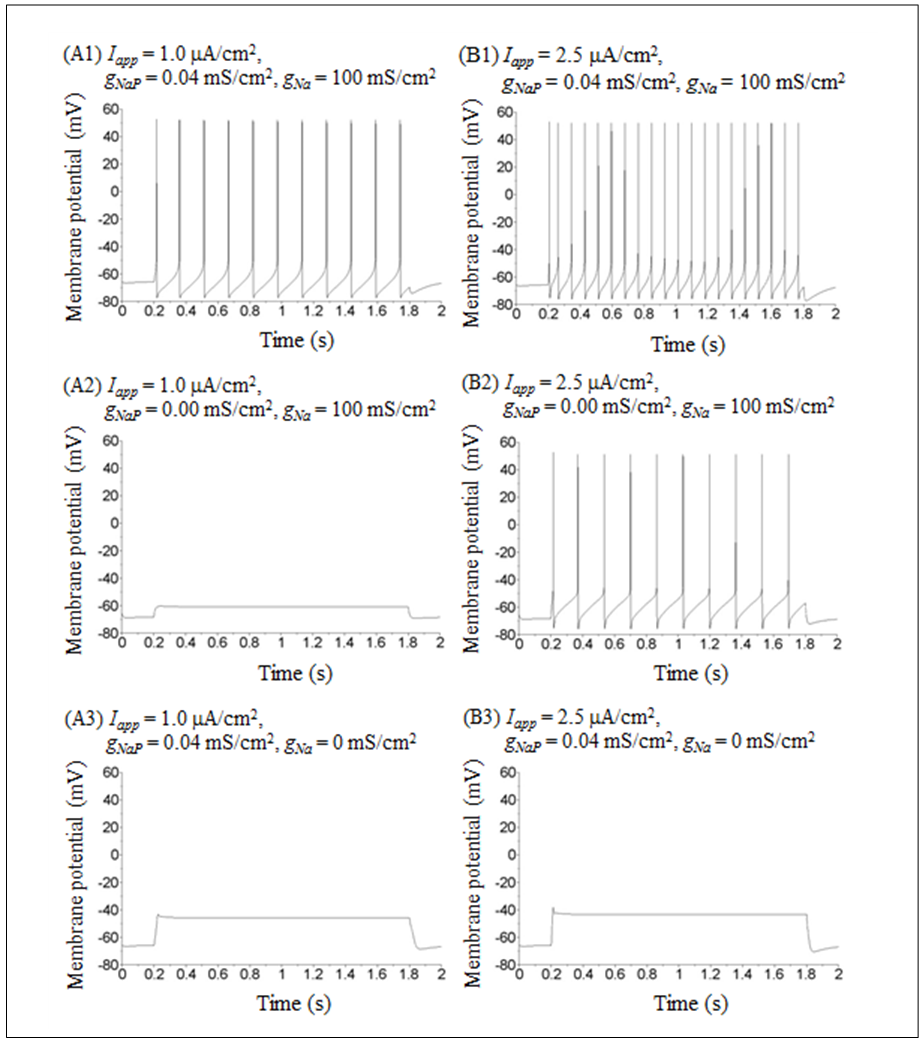 | Figure 1. Numerical simulation results of time evolution of the vMN model membrane potential. (A1) (Iapp, gNaP, and gNa) = (1.0 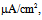 0.04 mS/cm2, and 100 mS/cm2). (A2) (Iapp, gNaP, and gNa) = (1.0 0.04 mS/cm2, and 100 mS/cm2). (A2) (Iapp, gNaP, and gNa) = (1.0 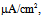 0.00 mS/cm2, and 100 mS/cm2). (A3) (Iapp, gNaP, and gNa) = (1.0 0.00 mS/cm2, and 100 mS/cm2). (A3) (Iapp, gNaP, and gNa) = (1.0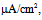 0.04 mS/cm2, and 0 mS/cm2). (B1) (Iapp, gNaP, and gNa) = (2.5 0.04 mS/cm2, and 0 mS/cm2). (B1) (Iapp, gNaP, and gNa) = (2.5 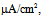 0.04 mS/cm2, and 100 mS/cm2). (B2) (Iapp, gNaP, and gNa) = (2.5 0.04 mS/cm2, and 100 mS/cm2). (B2) (Iapp, gNaP, and gNa) = (2.5 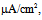 0.00 mS/cm2, and 100 mS/cm2). (B3) (Iapp, gNaP, and gNa) = (2.5 0.00 mS/cm2, and 100 mS/cm2). (B3) (Iapp, gNaP, and gNa) = (2.5 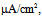 0.04 mS/cm2, and 0 mS/cm2) 0.04 mS/cm2, and 0 mS/cm2) |
The dynamical states of the vMN model at various gNaP and gNa values are shown in Figure 2. It was revealed that irrespective of Iapp, the (gNaP, gNa)-parameter space was divided into two dynamical states i.e., the repetitive spiking state (black circle) and the quiescent state (white circle). Figure 2 illustrates that irrespective of Iapp, the gNa range in which the repetitive spiking appeared decreased with a decrease in gNaP. When comparing Figures 2A and 2B, it was observed that when Iapp increased (Figure 2A → 2B), the area of the spiking state (black circle) expanded and the area of the quiescent state (white circle) shrunk. 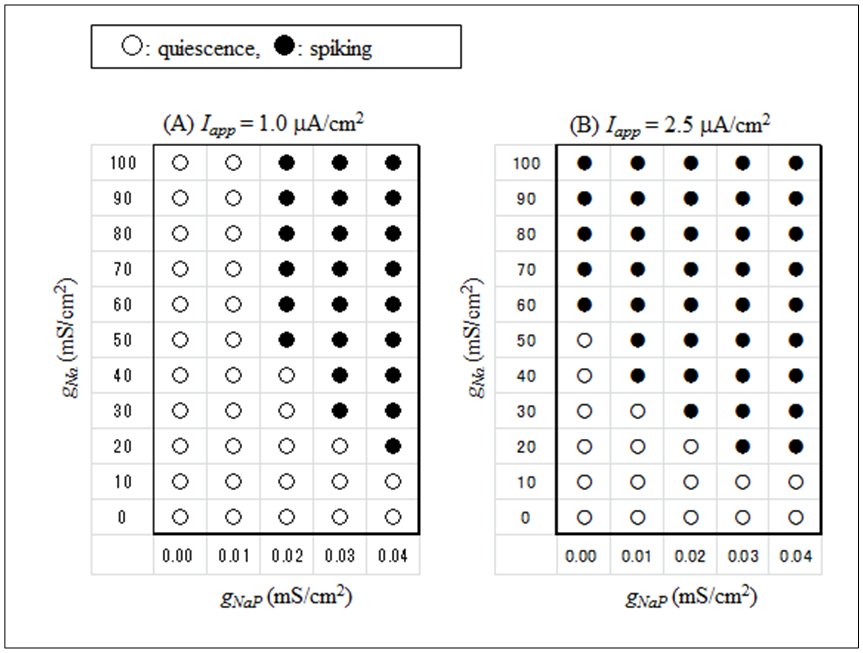 | Figure 2. Phase diagrams illustrating the dependence of the dynamical states of the vMN model on gNaP and gNa. (A) Iapp = 1.0 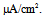 (B) Iapp = 2.5 (B) Iapp = 2.5 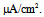 Black circle indicates the state of repetitive spiking, while white circle indicates the state of quiescence Black circle indicates the state of repetitive spiking, while white circle indicates the state of quiescence |
4. Discussions
The present study revealed the sensitivity of the spiking activity to variations of two types of sodium conductance. In contrast to a previous study [10], the present study clearly indicates the roles of different types of sodium conductance: a transient sodium conductance is indispensable to the repetitive spiking irrespective of the amplitude of injected current (Figures 1A3 and 1B3), while the necessity of a persistent sodium conductance in the repetitive spiking is dependent on the amplitude of injected current i.e., when the amplitude is large, the persistent sodium conductance is not indispensable (Figure 1B2), whereas it is indispensable when it is small (Figure 1A2).Based on previous studies, we can categorize the relationship between neuronal pacemaking and sodium conductance into two types. The first type consists of transient sodium conductance range in which pacemaking appears that decreases with a decrease in persistent sodium conductance such as in the amacrine cell model (Figure 2 in [8]). The second type consists of transient sodium conductance range in which pacemaking appears that increases with a decrease in persistent sodium conductance such as in the pyramidal neuron model (Figure 2 in [9]). The present results (Figure 2) indicate that the relationship between the vMN model pacemaking and sodium conductance can be categorized into the first type. When we carefully compare Figure 2 in [8] with Figure 2 in the present study, we found the following important difference: under excitable conditions, pacemaking in the amacrine model can occur in the absence of transient sodium conductance but cannot occur in the absence of persistent sodium conductance (see Figure 2A, 2B, and 2C in [8]), while pacemaking in the vMN model can occur in the absence of persistent sodium conductance but cannot occur in the absence of transient sodium conductance (see Figure 2B in the present study). In other words, we can categorize the first type further into the following two subtypes: one in which a persistent sodium conductance plays a more important role in pacemaking than a transient sodium conductance and the other in which a transient sodium conductance plays a more important role than a persistent sodium conductance.
5. Conclusions
The present study conducted a computational analysis of the vMN model. By integrating the results obtained in the present study and previous results, we can propose a new subtype regarding the relationship between neuronal pacemaking and different types of sodium conductance. This leads to a deeper understanding of the characteristics of sodium conductance, thus greatly contributing to a detailed analysis of membrane conductance of the neuron model.
ACKNOWLEDGEMENTS
The author would like to thank Enago (www.enago.jp) for the English language review.
References
| [1] | P. O. J. Scherer, S.F. Fischer, Theoretical Molecular Biophysics, Springer, 2010. |
| [2] | W. Lim, S. Y. Kim, “Strange nonchaotic oscillations in the quasiperiodically forced Hodgkin-Huxley neuron,” Journal of Physics A: Mathematical and Theoretical, vol. 42, no. 26, 265103 (13 pp), 2009. |
| [3] | M. Ashrafuzzaman and J. Tuszynski, Membrane Biophysics, Springer, 2012 |
| [4] | B. Doiron, C. Laing, A. Longtin, and L. Maler, “Ghostbursting: a novel neuronal burst mechanism,” Journal of Computational Neuroscience, vol. 12, no. 1, pp. 5-25, 2002. |
| [5] | T. Vo, R. Bertram, J. Tabak, and M. Wechselberger, “Mixed mode oscillations as a mechanism for pseudo-plateau bursting,” Journal of Computational Neuroscience, vol. 28, no. 3, pp. 443-458, 2010. |
| [6] | W. Teka, J. Tabak, T. Vo, M. Wechselberger, and R. Bertram, “The dynamics underlying pseudo-plateau bursting in a pituitary cell model,” The Journal of Mathematical Neuroscience, 1:12, 2011. |
| [7] | T. Vo, R. Bertram, and M. Wechselberger, “Multiple geometric viewpoints of mixed mode dynamics associated with pseudo-plateau bursting,” SIAM Journal on Applied Dynamical Systems, vol. 12, no. 2, pp. 789-830, 2013. |
| [8] | T. Shirahata, “The effect of variations in sodium conductances on pacemaking in a dopaminergic retinal neuron model,” Acta Biologica Hungarica, vol. 62, no. 2, pp. 211214, 2011. |
| [9] | T. Shirahata, “Effect of sodium conductance variations on electrical behavior of a neocortical neuron model,” Acta Biologica Hungarica, vol. 65, no. 4, pp. 379384, 2014. |
| [10] | O. Harish and D. Golomb, “Control of the firing patterns of vibrissa motoneurons by modulatory and phasic synaptic inputs: A modeling study,” Journal of Neurophysiology, vol. 103, no. 5, pp. 26842699, 2010. |
| [11] | J. Dörfl, “The musculature of the mystacial vibrissae of the white mouse,” Journal of Anatomy, vol. 135, no. 1, pp. 147154, 1982. |
| [12] | Q-T. Nguyen, R. Wessel, and D. Kleinfeld, “Developmental regulation of active and passive membrane properties in rat vibrissa motoneurones,” The Journal of Physiology, vol. 556, no. 1, pp. 203–219, 2004. |
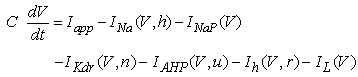

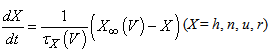
 (2)–(5)where C is the membrane capacitance
(2)–(5)where C is the membrane capacitance 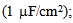 Iapp is the externally injected current of a constant amplitude; INa(V, h), INaP(V), IKdr(V, n), IAHP(V, u), Ih(V, r), and IL(V) denote the transient sodium current, persistent sodium current, delayed rectifier potassium current, calcium-dependent potassium current, hyperpolarization-activated h-current, and leak current, respectively, which are defined below in Equations (6)(11).
Iapp is the externally injected current of a constant amplitude; INa(V, h), INaP(V), IKdr(V, n), IAHP(V, u), Ih(V, r), and IL(V) denote the transient sodium current, persistent sodium current, delayed rectifier potassium current, calcium-dependent potassium current, hyperpolarization-activated h-current, and leak current, respectively, which are defined below in Equations (6)(11). 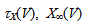 are time constants of activation/ inactivation and steady-state activation/inactivation functions, respectively, which are defined below in Equations (12)(19).
are time constants of activation/ inactivation and steady-state activation/inactivation functions, respectively, which are defined below in Equations (12)(19).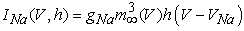
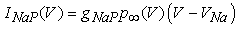
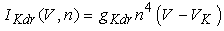
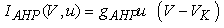
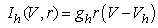
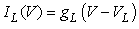
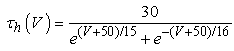
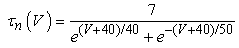
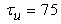
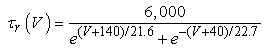
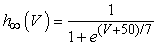
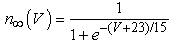
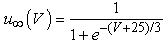
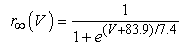
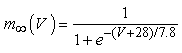
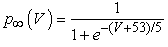
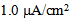 ) injected between 0.2 and 1.8 s. When the value of gNaP was decreased to zero while the other parameter values remained the same as in Figure 1A1, the spiking was completely blocked (Figure 1A2). When the value of gNa was decreased to zero while the other parameter values remained the same as in Figure 1A1, the spiking was also blocked (Figure 1A3). Figure 1B1 shows the repetitive spiking in response to a strong stimulus
) injected between 0.2 and 1.8 s. When the value of gNaP was decreased to zero while the other parameter values remained the same as in Figure 1A1, the spiking was completely blocked (Figure 1A2). When the value of gNa was decreased to zero while the other parameter values remained the same as in Figure 1A1, the spiking was also blocked (Figure 1A3). Figure 1B1 shows the repetitive spiking in response to a strong stimulus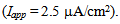 Under this condition, the spiking frequency was greater than that in Figure 1A1. Contrary to Figure 1A2, when the value of gNaP was decreased to zero with the other parameter values remaining the same as in Figure 1B1, the spiking was not blocked, but the spiking frequency decreased compared with that in Figure 1B1 (Figure 1B2). When the value of gNa was decreased to zero with the other parameter values remaining the same as in Figure 1B1, the spiking was completely blocked (Figure 1B3), which was similar to that in Figure 1A3.
Under this condition, the spiking frequency was greater than that in Figure 1A1. Contrary to Figure 1A2, when the value of gNaP was decreased to zero with the other parameter values remaining the same as in Figure 1B1, the spiking was not blocked, but the spiking frequency decreased compared with that in Figure 1B1 (Figure 1B2). When the value of gNa was decreased to zero with the other parameter values remaining the same as in Figure 1B1, the spiking was completely blocked (Figure 1B3), which was similar to that in Figure 1A3. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
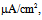 0.04 mS/cm2, and 100 mS/cm2). (A2) (Iapp, gNaP, and gNa) = (1.0
0.04 mS/cm2, and 100 mS/cm2). (A2) (Iapp, gNaP, and gNa) = (1.0 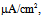 0.00 mS/cm2, and 100 mS/cm2). (A3) (Iapp, gNaP, and gNa) = (1.0
0.00 mS/cm2, and 100 mS/cm2). (A3) (Iapp, gNaP, and gNa) = (1.0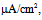 0.04 mS/cm2, and 0 mS/cm2). (B1) (Iapp, gNaP, and gNa) = (2.5
0.04 mS/cm2, and 0 mS/cm2). (B1) (Iapp, gNaP, and gNa) = (2.5 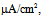 0.04 mS/cm2, and 100 mS/cm2). (B2) (Iapp, gNaP, and gNa) = (2.5
0.04 mS/cm2, and 100 mS/cm2). (B2) (Iapp, gNaP, and gNa) = (2.5 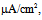 0.00 mS/cm2, and 100 mS/cm2). (B3) (Iapp, gNaP, and gNa) = (2.5
0.00 mS/cm2, and 100 mS/cm2). (B3) (Iapp, gNaP, and gNa) = (2.5 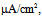 0.04 mS/cm2, and 0 mS/cm2)
0.04 mS/cm2, and 0 mS/cm2)
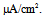 (B) Iapp = 2.5
(B) Iapp = 2.5 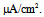 Black circle indicates the state of repetitive spiking, while white circle indicates the state of quiescence
Black circle indicates the state of repetitive spiking, while white circle indicates the state of quiescence