Vlad L. Negulescu
Correspondence to: Vlad L. Negulescu , .
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The mathematical model and calculus with Hyper-Complex Numbers are extensively presented. The representation of particles as Hyper-Complex Numbers and the concept of Physical World are further developed. Results concerning special relativity, electro-magnetism, light and matter-waves are consequently derived. Finally, it appears that this model conciliates the special relativity and quantum behaviour.
Keywords:
HC-numbers, Units multiplication table, Extension of Euler formula, Unit multipliers, 0I numbers, Function of HC-variables, Ideal particle as HC-number, Physical world, Axiom of motion, Composition of forces, Light -And matter waves
Cite this paper: Vlad L. Negulescu , Hyper-Complex Numbers in Physics, International Journal of Theoretical and Mathematical Physics, Vol. 5 No. 2, 2015, pp. 28-43. doi: 10.5923/j.ijtmp.20150502.03.
1. Introduction
In an article [1] published in 1997, the author developed the mathematical model of hyper-complex numbers and presented some of its applications in relativistic mechanics. The present paper is enhancing the main aspects of the hyper-numbers representation; bringing new concepts and ideas.
2. Calculus with Hyper-Complex Numbers
2.1. Definition
Hyper-complex numbers, or H-numbers, are ordered pairs of complex numbers which follow certain computation rules [1], and belong to a set H. One element p of the set H represents a unique H- number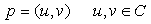 | (2.1) |
where C denotes the set of complex numbers.The basic rules of H- numbers are further presented:a) EqualityTwo H-numbers 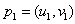 and
and 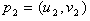 are equal if and only if,
are equal if and only if,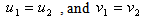 | (2.2) |
b) AdditionThe addition is a binary operation on the set H, defined as: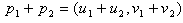 | (2.3) |
where the sign + in the right member has its usual meaning, i.e. normal addition between complex numbers.c) Multiplication of H-numbersThe multiplication is a binary operation on the set H, defined as follows: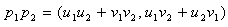 | (2.4) |
Multiplication satisfies the following three conditions:(i) For all  commutativity holds i.e.
commutativity holds i.e. (ii) For all
(ii) For all 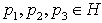 associativity holds i.e.
associativity holds i.e. 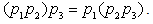 (iii) For all
(iii) For all 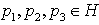 distributivity related to addition (as defined at the point b above) holds, i.e.
distributivity related to addition (as defined at the point b above) holds, i.e.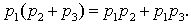 The following fundamental units are denominated: - the number
The following fundamental units are denominated: - the number 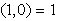 is the real unit;- the number
is the real unit;- the number 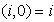 is the imaginary unit;- the number
is the imaginary unit;- the number 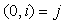 is the co-imaginary unit;- the number
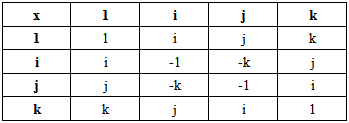
is the co-imaginary unit;- the number 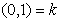 is the co-real unit.Applying the multiplication rule (2.4), we obtain the units multiplication table.
is the co-real unit.Applying the multiplication rule (2.4), we obtain the units multiplication table. Table 1. Units’ Multiplication Table
 |
| |
|
2.2. The Rectangular form of an H-Number
According to the addition rule (2.3) we may write: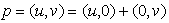 | (2.5) |
Using the basic rules c and the units’ definitions, we arrive at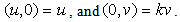 Replacing this into (2.5) we have
Replacing this into (2.5) we have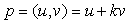 | (2.6) |
But complex numbers u and v can be also written using their usual rectangular form: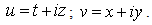 | (2.7) |
Introducing the expressions (2.7) in (2.6) and using Table 1, we obtain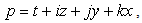 | (2.8) |
where t is the real part, z is the imaginary part, y is the co-imaginary part , and x is the co-real part of p, or: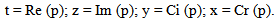 An H-number written as in (2.8) can be represented as a point
An H-number written as in (2.8) can be represented as a point  in a four-dimensional space, named hyperspace, using a Cartesian coordinates system with four reciprocally perpendicular axes:- the real axis, with its unit 1,- the imaginary axis, with its unit i,- the co-imaginary, axis with its unit j,- the co-real axis, with its unit k.This point is called the image of the H-number in the hyperspace. Alternatively the image can be the vector OP. Reciprocally, every point P, or vector OP, of the hyperspace has a correspondent H-number which is named the affix of the point P.Between the hyperspace’s points and H-numbers is thus established a one-to-one correspondence. The origin O of the coordinate system represents the image of H-number zero.
in a four-dimensional space, named hyperspace, using a Cartesian coordinates system with four reciprocally perpendicular axes:- the real axis, with its unit 1,- the imaginary axis, with its unit i,- the co-imaginary, axis with its unit j,- the co-real axis, with its unit k.This point is called the image of the H-number in the hyperspace. Alternatively the image can be the vector OP. Reciprocally, every point P, or vector OP, of the hyperspace has a correspondent H-number which is named the affix of the point P.Between the hyperspace’s points and H-numbers is thus established a one-to-one correspondence. The origin O of the coordinate system represents the image of H-number zero.
2.3. The Extension of the Euler's Formula
Let us consider the function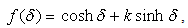 | (2.9) |
where δ∈ C is a complex variable and k is the co-real unit. The expression (2.9) can be differentiated with respect to δ because both functions, hyperbolic sine and hyperbolic cosine, are analytical in C, except the point at infinity. The derivative is: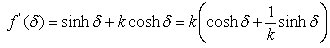 But because k = 1/k, we obtain
But because k = 1/k, we obtain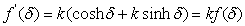 | (2.10) |
The general solution of the differential equation (2.10) is given by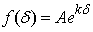 | (2.11) |
where A is a constant. Comparing (2.9) and (2.11) for δ = 0, the value of A is found to be 1. Thus, the final result takes the following form: 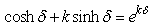 | (2.12) |
This is valid for all δ∈ C, except for the point at infinity.
2.4. The Exponential Representation; Complex Modulus and Norm
Let us consider an H-number: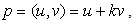 where u, v∈ C, and u2 ≠ v2By definition the complex modulus of p is:
where u, v∈ C, and u2 ≠ v2By definition the complex modulus of p is: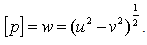 | (2.13) |
But w may be written as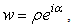 | (2.14) |
where ρ>0, is called the norm of p, and α is the imaginary argument of p. The norm of p is denoted by 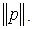 For convenience we write:
For convenience we write: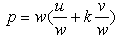 | (2.15) |
Now, introducing the argument 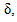 we replace
we replace 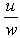 and
and 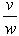 as follows:
as follows: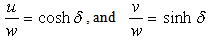 | (2.16) |
The argument 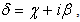 is a complex number, and will be further called Hyperbolic Complex Argument (HCA).Substituting (2.14) and (2.16) into (2.15) one obtains:
is a complex number, and will be further called Hyperbolic Complex Argument (HCA).Substituting (2.14) and (2.16) into (2.15) one obtains: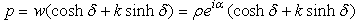 | (2.17) |
By applying the Euler's extended formula we arrive at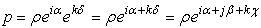 | (2.18) |
ρ is norm of p, α is the imaginary argument, β co-imaginary argument, and χ co-real argument.As we can easily see, this representation is not suitable for H-numbers with u = ± v. In this case ρ = 0 but χ = ± ∞ and the extended Euler's formula does not apply anymore.
2.5. The Hyperspace Generated by Planes; Complex Distance
Let us consider a set in H with its elements having the form 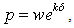 where δ is a complex constant.If w takes all values of the set C, then the image of p is a plane in the hyperspace. When ð varies, the resulting family of planes will generate and cover the hyperspace. The variable ð belongs to the domain in the complex plane (χ, β) bordered by the lines β=0 and
where δ is a complex constant.If w takes all values of the set C, then the image of p is a plane in the hyperspace. When ð varies, the resulting family of planes will generate and cover the hyperspace. The variable ð belongs to the domain in the complex plane (χ, β) bordered by the lines β=0 and 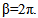 The following expressions represent the transformation from rectangular to exponential coordinates.
The following expressions represent the transformation from rectangular to exponential coordinates.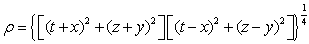 | (2.19) |
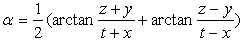 | (2.20) |
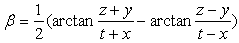 | (2.21) |
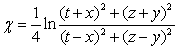 | (2.22) |
Because of the periodicity of 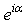 and respectively
and respectively 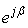 , a
, a 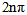 can be added to arguments α and β, where n is an arbitrary integer. If v=0, then the H-number will be reduced to a simple complex number, u, and its complex modulus will be
can be added to arguments α and β, where n is an arbitrary integer. If v=0, then the H-number will be reduced to a simple complex number, u, and its complex modulus will be 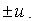 The norm becomes the absolute value of u. Let us make the following notations:
The norm becomes the absolute value of u. Let us make the following notations: 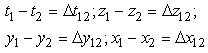 By extension of (2.13) and (2.19) we will define the complex gap, s12, and respectively the norm-distance, l12, between two H-numbers, p1 and p2. Please see 2.23 and 2.24.
By extension of (2.13) and (2.19) we will define the complex gap, s12, and respectively the norm-distance, l12, between two H-numbers, p1 and p2. Please see 2.23 and 2.24.
2.6. Fundamental Planes
An H number is univocally defined if we have the projections of its image on the three fundamental planes. These fundamental subspaces are:a. 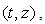 or the 1st fundamental plane;b.
or the 1st fundamental plane;b. 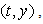 or the 2nd fundamental plane;c.
or the 2nd fundamental plane;c. 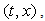 or the 3rd fundamental plane.
or the 3rd fundamental plane.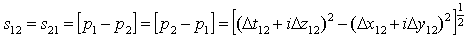 | (2.23) |
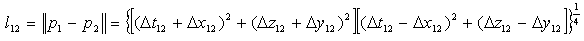 | (2.24) |
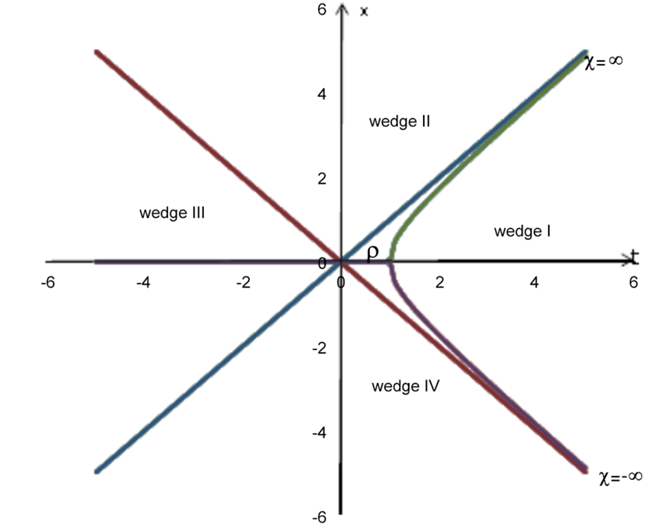 | Figure 1. The 3rd fundamental plane or the plane (t, x) |
Let us analyse the expression (1.18) which represents the exponential form of an arbitrary hyper-number. For β=0 and χ=0 the formula (2.18) will become 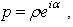 and represents the first fundamental plane for
and represents the first fundamental plane for  and
and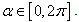 For α=0 and χ=0 we get:
For α=0 and χ=0 we get: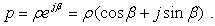 This is the second fundamental plane for
This is the second fundamental plane for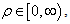 and
and 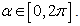 For α=0 and β=0 the expression becomes
For α=0 and β=0 the expression becomes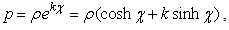 which for
which for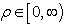 and
and 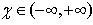 will represents only the wedge I shown in the Figure 1, above. The hyperbola represents the locus of points with ρ constant, belonging to wedge I.Following expressions are valid for H-numbers belonging to others wedges of the plane (t, x).
will represents only the wedge I shown in the Figure 1, above. The hyperbola represents the locus of points with ρ constant, belonging to wedge I.Following expressions are valid for H-numbers belonging to others wedges of the plane (t, x).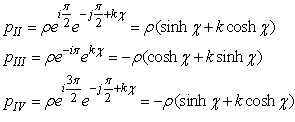 | (2.25) |
2.7. The Transformation from Exponential to Rectangular
Let us consider an H- number represented in the exponential form. The rectangular components of the above number are given by: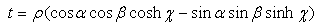 | (2.26) |
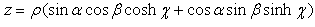 | (2.27) |
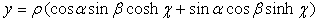 | (2.28) |
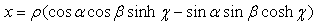 | (2.29) |
An alternative development yields to: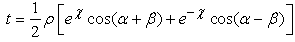 | (2.30) |
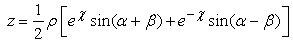 | (2.31) |
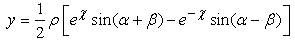 | (2.32) |
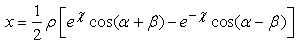 | (2.33) |
By similarity with vectors, the magnitude of an H-number can be defined as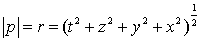 | (2.34) |
The following two relations can be further developed: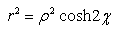 | (2.35) |
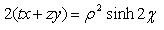 | (2.36) |
The relation (2.35) states that the magnitude of an H-number is bigger than or equal with its norm.
2.8. Interrelated Numbers
a. The conjugate H-numberIf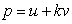 , where
, where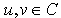 , then its conjugate H-number
, then its conjugate H-number 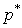 is defined as,
is defined as, 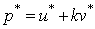 , where
, where 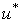 and
and 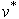 represent the complex conjugates of u and v.
represent the complex conjugates of u and v.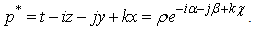 | (2.37) |
b. The reciprocal H-numberBy definition the reciprocal H-number of p is: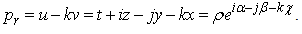 | (2.38) |
c. The replicate H-numberBy definition the replicate H-number of p is: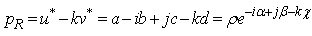 | (2.39) |
It can be easily seen that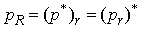 | (2.40) |
Further the following relations can be written: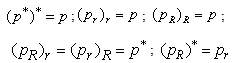 | (2.41) |
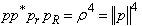 | (2.42) |
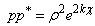 | (2.43) |
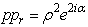 | (2.44) |
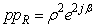 | (2.45) |
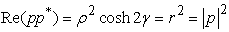 | (2.46) |
If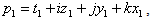 and
and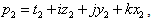 then
then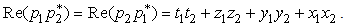 | (2.47) |
2.9. The Angle between Two Image Vectors
Applying the rule of the scalar product, the cosine of the angle between two image vectors, 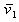 (corresponding number
(corresponding number 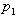 ) and
) and 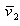 (corresponding number
(corresponding number 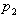 ), can be written as:
), can be written as: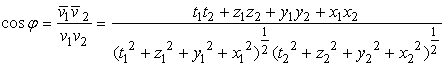 | (2.48) |
In the formula above v1 and v2, are the corresponding magnitudes of image vectors.We may write (2.48) alternately: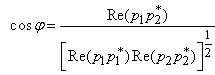 | (2.49) |
Using the exponential form and applying formulas (2.26) and (2.46), one obtains finally: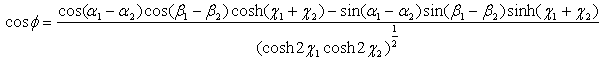 | (2.50) |
2.10. Unit Multipliers
An H-number with ρ = 1 will be named a unit multiplier. Two particular groups of unit multipliers can be further defined: rotors and pseudo-rotors. A rotor is a unit multiplier having the following expression: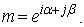 | (2.51) |
Let D be a subset of H and Δ the image of this subset in the hyperspace. If every element p∈ D is multiplied by the same arbitrary rotor, then a new subset D° will be obtained. The image of D° in the four-dimension space is Δ°.Theorem 2.1The image subsets Δ and Δ° are geometrically identical and superposable.Multiplication by a rotor conserves the magnitude and the angle and thus the demonstration of the above theorem is almost evident. This is why this multiplication is named rotation.A pseudo-rotor is a unit multiplier having the expression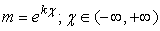 | (2.52) |
Consequently the multiplication is called pseudo-rotation.It is easy to see that:- The 1st fundamental plane conserves itself after an arbitrary rotation by 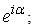 - The 2nd fundamental plane conserves itself after an arbitrary rotation by
- The 2nd fundamental plane conserves itself after an arbitrary rotation by 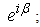 -Each wedge of the 3rd fundamental plane conserves itself after a pseudo-rotation.
-Each wedge of the 3rd fundamental plane conserves itself after a pseudo-rotation.
2.11. The Hyper-Volume
Let us find the volume (content) element in a four-dimension Euclidean space using the H-numbers‘exponential representation. We will differentiate the expression (2.18) obtaining the four basic vectors of the elementary cell: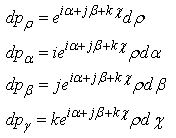 | (2.53) |
The multiplication by the rotor 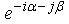 does not change the form of the cell´s image and thus the differential hyper-volume is:
does not change the form of the cell´s image and thus the differential hyper-volume is: 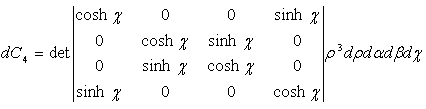 | (2.54) |
The value of the determinant is 1 and thus the elementary hyper-volume is: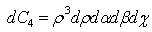 | (2.55) |
Starting from the above equation we can develop some interesting applications.1. Let D be a subset of H and Δ the image of this subset in the hyperspace. If every element p∈ D is multiplied by the same arbitrary pseudo-rotor 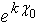 , then a new subset D° will be obtained. The image of D° in the hyperspace is Δ°.Δ and Δ° have the same hyper-volume.The proof is based on the fact that the pseudo-rotation does not change the elementary volume.2. Now we use the expression of the elementary hyper-volume (2.55) and integrating it for
, then a new subset D° will be obtained. The image of D° in the hyperspace is Δ°.Δ and Δ° have the same hyper-volume.The proof is based on the fact that the pseudo-rotation does not change the elementary volume.2. Now we use the expression of the elementary hyper-volume (2.55) and integrating it for 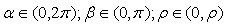 we get:
we get: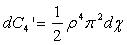 | (2.56) |
The equation of a four-dimensional sphere with radius R and the centre at the origin has the expression (see 2.35), 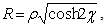 and thus the formula above becomes:
and thus the formula above becomes: 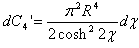 Doing the integral we obtain the volume of the four-dimensional sphere:
Doing the integral we obtain the volume of the four-dimensional sphere: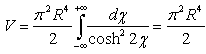 | (2.57) |
3. A subset of H- numbers having the same norm ρ has as image a super- hyperboloid in the hyperspace. Using (2.53) we obtain, for ρ constant, the following differential vectors: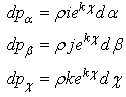 The content of this elementary cell is:
The content of this elementary cell is: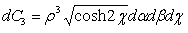 | (2.58) |
We build a super-tetrahedron using the elementary cell and the point O (origin of axes).Its four dimension volume is: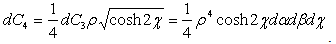 Integrating we obtain the four- dimension volume bordered by the super hyperboloid:
Integrating we obtain the four- dimension volume bordered by the super hyperboloid: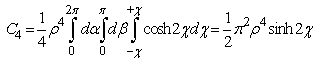 | (2.59) |
It is clear that for any 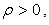 the hyper-volume tends to infinity when
the hyper-volume tends to infinity when 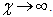 For
For 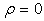 the hyper-volume is indeterminate and can have eventually a finite value.
the hyper-volume is indeterminate and can have eventually a finite value.
2.12. Zero-Interval (0I) Subsets and Bases
As we have already seen in paragraph 2.4., there are some H-numbers which cannot be exponentially represented. These numbers have the following form: 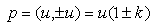 | (2.60) |
They are named Zero Interval (0I) numbers. The image of a 0I number belongs to one of the two 0I basic planes in the hyperspace. If the images of two arbitrary numbers belong either to one of 0I basic planes or to one parallel with them, then the complex gap and the norm-distance between these numbers (as were defined in paragraph 2.5) are zero. These planes are generally named 0I planes. There are two categories of such planes, 0I+ or b like, and 0I- or 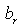 like.It is clear that for any 0I number the complex modulus is zero and the hyperbolic complex argument δ represents the point at infinity. The expression (2.60) shows that every 0I-number can be written as a product of an ordinary complex number with either (1 + k) or (1 - k). Let us define now two particular numbers which are called bases:
like.It is clear that for any 0I number the complex modulus is zero and the hyperbolic complex argument δ represents the point at infinity. The expression (2.60) shows that every 0I-number can be written as a product of an ordinary complex number with either (1 + k) or (1 - k). Let us define now two particular numbers which are called bases: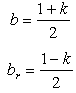 | (2.61) |
The main properties of bases will be further presented.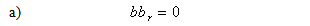 | (2.62) |
The image vectors are evidently perpendicular. 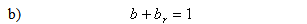 | (2.63) |
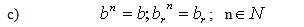 | (2.64) |
d) Expressions like 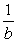 and
and 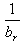 have no mathematical sense in H.e) The following relations are valid:
have no mathematical sense in H.e) The following relations are valid: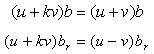 | (2.65) |
f) Following identities can be also developed: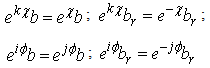 | (2.66) |
2.13. Bases’ Representation
Let us remember which forms of an H-number were used until now.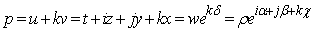 | (2.67) |
By multiplying (2.67) with the number 1, written as under (2.63), and using the properties of bases the following expressions will be obtained: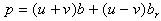 | (2.68) |
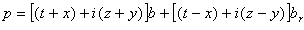 | (2.69) |
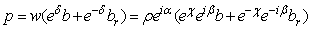 | (2.70) |
In some cases the basses’ representation can offer certain advantages as we will see latter.
2.14. Functions of an H-Number Variable, or HC Functions
Consider E and F two subsets of the set H, with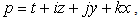 and
and 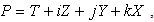 their corresponding elements.Let ΔE and ΔF be images of subsets E and F in the hyperspace.A function, or a map, f associates to each element p∈ E an element P∈ F, and can be written as:
their corresponding elements.Let ΔE and ΔF be images of subsets E and F in the hyperspace.A function, or a map, f associates to each element p∈ E an element P∈ F, and can be written as: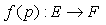 | (2.71) |
The arbitrary element 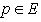 is called the H-number variable. The derivative of the function f (p) in
is called the H-number variable. The derivative of the function f (p) in 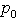 is defined as:
is defined as: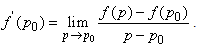 If the derivative at p0 is unique, for all paths in hyperspace, then the function is said to be monogenic at this point (we just extended the definition [2] used for functions of complex variables). A monogenic function in p satisfies at the image point of p, in the four dimensional space, the following equations:
If the derivative at p0 is unique, for all paths in hyperspace, then the function is said to be monogenic at this point (we just extended the definition [2] used for functions of complex variables). A monogenic function in p satisfies at the image point of p, in the four dimensional space, the following equations: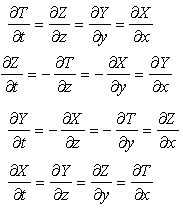 | (2.72) |
The equalities (2.72) will be named the extended Cauchy-Riemann’s equations.The demonstration can be easily performed using the differentials of functions T, Z, Y, X and considering the uniqueness of the derivative of f (p). A function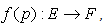 which is monogenic in every point of a subset D⊂ E is said to be monogenic on the subset D or holomorphic [3] on D.The following properties are valid.Property #1.If f(p) is holomorphic on D and its derivative is zero in all points p∈D, then f is a constant on the subset D.Property #2
which is monogenic in every point of a subset D⊂ E is said to be monogenic on the subset D or holomorphic [3] on D.The following properties are valid.Property #1.If f(p) is holomorphic on D and its derivative is zero in all points p∈D, then f is a constant on the subset D.Property #2 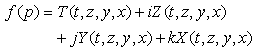 If the function above is holomorphic on D and T, Z, Y, X have their second degree derivatives continuous on the image of D, then the functions T, Z, Y, X satisfy the following system of differential equations:
If the function above is holomorphic on D and T, Z, Y, X have their second degree derivatives continuous on the image of D, then the functions T, Z, Y, X satisfy the following system of differential equations: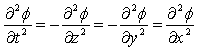 | (2.73) |
Property #3If f (p) is holomorphic on D and if the functions T, Z, Y, X, have their fourth degree derivatives continuous on the image of D, then these functions satisfy the following equations: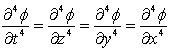 | (2.74) |
The Euler formula can be further extended for H-number variables: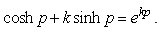 | (2.75) |
The expression (2.75) is valid for any p∈H, except the point at infinity.A curve in the four-dimension space is represented by a function of a real variable 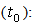
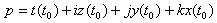 | (2.76) |
The differential norm- length of the curve is: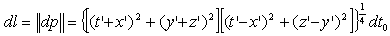 | (2.77) |
The apostrophe signifies the derivative in respect to t0.Similarly with the length of a curve in the Euclidean space, the norm- length of the curve will be obtained integrating the expression (2.77).
2.15. The Development of an H- Function Using 0I Basic Numbers
According to (2.68) and (2.69) a hyper-number variable may be also written as: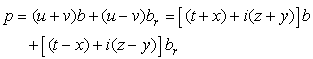 | (2.78) |
Theorem 2.2If the function 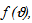 where
where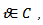 is an analytic one, then:
is an analytic one, then: 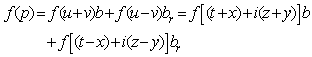 | (2.79) |
The proof is based on the fact that all cross-products having the form 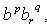 where
where 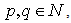 are zero. The above theorem reduces the study of functions with the H-number variable to the ordinary case of functions of complex variable.Now let us write:
are zero. The above theorem reduces the study of functions with the H-number variable to the ordinary case of functions of complex variable.Now let us write: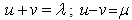 | (2.80) |
By using this complex variables ‘change the formula (2.79) becomes: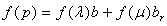 | (2.81) |
When λ or μ is constant the equation (2.81) will describe a 0I plane.Theorem 2.3.A holomorphic function transforms a 0I plane into another 0I plane, keeping the sign. The proof is easy for an analytic function when we use the expression (2.81).
2.16. Conservative Mapping and the Curvature of a Surface
Let us write again the equation (2.17) replacing w by p0∈C, δ being a complex constant.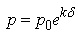 | (2.82) |
The above equation represents a plane in a four-dimension space. If we differentiate it, then we get: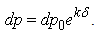 | (2.83) |
It is evident that 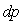 and
and 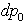 have the same complex modulus. We will say that the mapping p0 →p, performed by (2.82), is conservative. In general a conservative map fulfils the equation (2.83) i.e. it conserves the differential complex modulus. The HCA, δ is no more a constant but a holomorphic function of a complex variable p0.A conservative map transforms a domain belonging to complex plane C into a surface Σ in hyperspace. Its corresponding equation is:
have the same complex modulus. We will say that the mapping p0 →p, performed by (2.82), is conservative. In general a conservative map fulfils the equation (2.83) i.e. it conserves the differential complex modulus. The HCA, δ is no more a constant but a holomorphic function of a complex variable p0.A conservative map transforms a domain belonging to complex plane C into a surface Σ in hyperspace. Its corresponding equation is: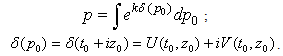 | (2.84) |
A transformation using this map is conformal, i.e. it preserves both the angles and the shape of infinitesimally small figures [4]. A line parallel to the real axis of the complex plane will be transformed into a curve 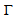 on the surface Σ. In this case t0 is the arc norm- length of the curve
on the surface Σ. In this case t0 is the arc norm- length of the curve 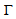 , i.e. this curve is parameterized by its arc norm- length (see 2.77). The complex curvature of the surface Σ is defined as:
, i.e. this curve is parameterized by its arc norm- length (see 2.77). The complex curvature of the surface Σ is defined as: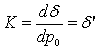 | (2.85) |
The curve 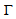 as defined above has an “arc norm- length”-curvature:
as defined above has an “arc norm- length”-curvature: 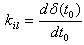 | (2.86) |
Please compare (2.86) with the definition of the Euclidean radius of curvature [5].
2.17. Conclusions
The hyper-numbers represent a new kind of extension of complex numbers. Unlike other extension models, see quaternions, this one shows a commutative multiplication. The hyper-complex numbers differ from bicomplex numbers or tessarines in their multiplication tables. As we will see further the pseudo-rotation of hyper-complex number is paramount for their physical applications.
3. Applications in Special Relativity and Electromagnetism
3.1. Pseudo-Rotation and Its Similarity to Lorenz Transformation
Let us consider the hyperspace and an axes coordinate system, S. We define now a transformation of axes generated by a pseudo-rotation of antireal argument –χ.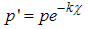 | (3.1) |
where p and p’ are the affixes of the same point with reference to the coordinate systems S and respectively S’. Processing (3.1) we obtain the relationships between the old and the new coordinates: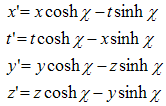 | (3.2) |
The relations (3.2) are definitely some kind of déjà-vu, being similar to Lorenz transformation equations [6]. This similarity brought us to the idea to associate a material particle with an H-number.
3.2. The Ideal Particle as H-number; Physical World
Let us consider an ideal particle which is characterized by four basic parameters: time (t), mass (z), momentum(y) and position in space(x). These parameters can be measured by an observer carrying specific measuring instruments and bound to an observational frame of reference. The parameter time “flows” in one direction and is recorded by the observer’s clock.The observer will display the result of his measurements on the particle, using an appropriate coordinate system. The position in space and the momentum are normally three- dimensional vectors but, for simplicity reasons, let us consider first only the case when these two parameters are scalars. Thus the four basic parameters of an arbitrary particle become the coordinates of a point P in a four dimensional space, the so called 'physical world'.Axiom #1 The 'physical world' and the set H of hyper-numbers are isomorphic groups. A subset of points in the 'physical world' corresponds to a subset of H-numbers in H.According to this axiom a particle described by its t, z, y, and x is associated with an H-number 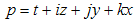 | (3.3) |
All four basic parameters of an ideal particle have to be measured using a common unit. This unit can be, for example, the length unit, the meter. An adequate system is the geometrized unit (GU) system [7], where the speed of light in vacuum c, and gravitational constant G, are considered to be equal to 1. The connection with the International System of Units (SI) is shown in the Table 2.Table 2. The direct and reversed conversion SI- GU
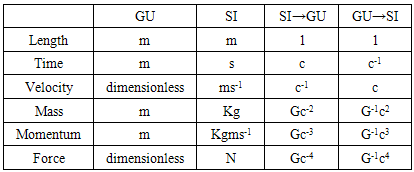 |
| |
|
We can conclude that the “physical world “is a metric space [8] with the metric (distance function) given by the formula 2.24.This metric melts together all four basic parameters, which are inextricably connected and transform each other. In according to (2.23), the complex gap between two infinitely close points of the 'physical world’ is given by: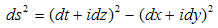 | (3.4) |
The differential norm-distance (see 2.24) has the following expression: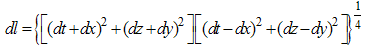 | (3.5) |
The expression (3.5) can be processed to: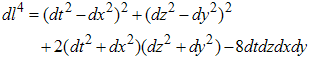 | (3.6) |
This form remains valid when space and momentum are vectors if the following replacements are made: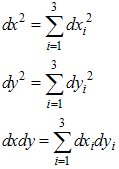 | (3.7) |
The “physical world” is not static because the time is varying continuously. An observed particle will follows a curve in H, called the evolution line of this particle. A particle is said to be in motion if x, the anti-real part of the corresponding number, is changing with t. The evolution line represents evidently an extension of the world line [9] used in special relativity. If we consider now the equations (3.2), then it is obvious that the first two equations represent the Lorenz transformation equations. The last two equations show relativistic transformations of the momentum and mass. The parameter 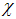 represents the relative rapidity [10] of the coordinate system S’ with respect with the old one S. The velocity of S’ relative to S has the expression:
represents the relative rapidity [10] of the coordinate system S’ with respect with the old one S. The velocity of S’ relative to S has the expression: 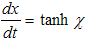
3.3. The Invariance of the Speed of Light
As we know (see paragraph 2.12), there are H-numbers having their images located on 0I planes. According to the theorem 2.3, these numbers keep the zero interval separation between them after any arbitrary transformation through a holomorphic function. Their correspondents in the 'physical world' are evolution lines of light particles (photons). A photon is associated with following H-numbers: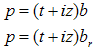 The real, physically observable photon must have a non-zero mass/ momentum z, otherwise it is elusive. The evolution line of a photon will be also named light-path. Once this correspondence has been stated, the theorem 2.3 can be reformulated as follows:Any coordinates transformation performed by a holomorphic function will transform a light-path into another light-path.This fundamental theorem represents a generalisation of the Einstein's law of light propagation.An equivalent formulation of the above theorem is: the speed of light is an invariant (1 in GU system) for any such coordinates transformation.
The real, physically observable photon must have a non-zero mass/ momentum z, otherwise it is elusive. The evolution line of a photon will be also named light-path. Once this correspondence has been stated, the theorem 2.3 can be reformulated as follows:Any coordinates transformation performed by a holomorphic function will transform a light-path into another light-path.This fundamental theorem represents a generalisation of the Einstein's law of light propagation.An equivalent formulation of the above theorem is: the speed of light is an invariant (1 in GU system) for any such coordinates transformation.
3.4. The ST Plane or the Minkowski Space
When the particle moves, the observer “sees” only the world line, i.e. the projection of the particle’s evolution line on the third fundamental subspace (paragraph2.6). The 3rd fundamental space, also named ST plane, extended for a three-dimensional space component is evidently the Minkowski space-time. The first and the third wedge of the diagram presented in Fig.1 represent the future and respectively the past. The wedge II and the wedge IV belong to the region between light cones known as “elsewhere”. The differential space-time interval, as was defined in the special relativity, will be obtained from (3.4) by nullifying z and y.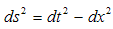 | (3.8) |
3.5. The Collision of Particles; Conservation of Mass and Momentum
Two or more particles are said to be at collision if their images in hyperspace have the same ST coordinates. The collision occurs as an event (t0, x0) in the continuous space-time. For all associated hyper-numbers following condition are fulfilled: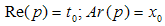 | (3.9) |
Images of these hypernumbers belong to a plane in hyperspace named the dynamic plane of the event (t0, x0). Considering the homogeneity and continuity of the space-time the following equation must be valid: 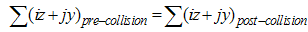 | (3.10) |
The above equation takes finally the following form: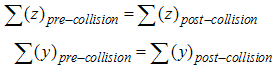 | (3.11) |
Relations (3.11) represent the laws of mass and momentum conservation. In the general case, the momentum is a vector and the second equation will contain vectorial components.
3.6. The Generalized Pseudo-Rotation Transformation
The formulas (3.2) were given for the simple case of scalar space and momentum. For the general case, where 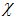 , y and x are vectors, should be considered that the pseudo-rotation acts on t, z and only on the components of x and y parallel to the vector representing the anti-real argument:
, y and x are vectors, should be considered that the pseudo-rotation acts on t, z and only on the components of x and y parallel to the vector representing the anti-real argument: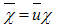 | (3.12) |
The expression 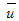 denotes a unit vector and
denotes a unit vector and 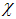 represents the magnitude of
represents the magnitude of 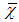 . Thus the general pseudo-rotation transformation equations are:
. Thus the general pseudo-rotation transformation equations are: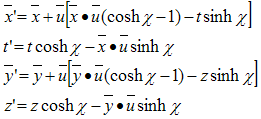 | (3.13) |
The expression 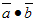 represents the scalar products of two arbitrary vectors. The formula of velocity’s transformation can be obtained by differentiation:
represents the scalar products of two arbitrary vectors. The formula of velocity’s transformation can be obtained by differentiation: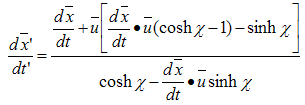 | (3.14) |
Making 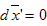 , one obtains the velocity of S’ relative to S:
, one obtains the velocity of S’ relative to S: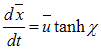 | (3.15) |
3.7. The Axiom of the Motion
As you have seen, the four basic particle's parameters were introduced like a kind of “deus ex machina”, without insisting on their physical significance. I intentionally made no reference to the laws governing particle mechanics or to the experimental support for this approach.My intention was to state a general axiom of the mechanical motion based on the H-numbers representation of particles. The logical consequence of this axiom will be laws of particle mechanics, in according with the empirical evidence, and encompassing the special relativity. Now let us consider a particle with an observer spatially attached to it. In this particular reference system the particle's evolution line stays in the complex plane C. The above reference frame represents the rest frame of the particle, as was defined in the special relativity theory. The time measured by the observer in this frame is the so-called proper time 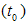 . The mass of the particle represents evidently the rest mass (z0). The observer records only these two parameters and the particle's evline is expressed by:
. The mass of the particle represents evidently the rest mass (z0). The observer records only these two parameters and the particle's evline is expressed by: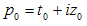 | (3.16) |
Axiom #2The mechanical motion of a particle is represented by a conservative mapping (see the paragraph 2.16) of C on H. The motion means a coordinate-transformation from the proper frame to an exterior one. The particle is now seen by an observer attached to another reference frame, distinct from the particle's proper frame.The differential form of a conservative mapping is given by the equation (2.83), where 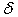 is an analytic function expressed as in the equation (2.84):
is an analytic function expressed as in the equation (2.84):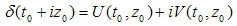 | (3.17) |
With all this, the conservative mapping of C on H is expressed by the following relation: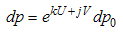 | (3.18) |
The functions U and V are respectively called rapidity and vigor.
3.8. General Equations of the Particle’s Motion; Mass and Momentum
Processing (3.18) one obtains the general equations of the particle’s motion in differential format: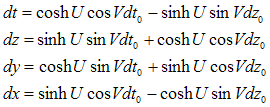 | (3.19) |
The equations are given for the simple case of one-dimensional lengths and momenta. For the further analysis, the expressions (3.19) are sufficient, but we should keep in mind that U and V are vectors.The equation (3.18) shows that differentials 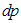 and
and 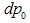 have the same complex modulus and thus:
have the same complex modulus and thus: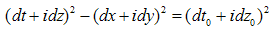 | (3.20) |
Equalizing real and imaginary parts we obtain the implicit form of the equations of the motion: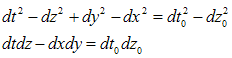 | (3.21) |
Using formulas (3.7) the implicit equations (3.21) can be easily extended when space and momentum are vectors.The rest mass of the moving object expressed in meter is, for most practical cases, very small.With this assumption we may write: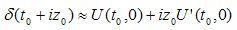 | (3.22) |
where U’ is the derivative of U with respect to t0.Following approximations are allowed: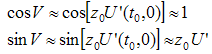 | (3.23) |
Introducing (3.23) in the second and third equation of (2.19) we get: 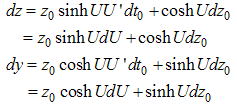 | (3.24) |
The above equations integrate to: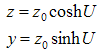 | (3.25) |
They represent the familiar relativistic expression of mass and momentum. About these expressions and their meaning there are still a lot of discussions and controversy [11]. The model and the deduction presented above could bring a contribution to this theme.
3.9. Motion with Constant Rest Mass
Let us now look closer at the second equation of the system (3.21). When the rest mass of the particle remains constant it reduces to: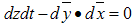 For convenience this equation can be re-written as:
For convenience this equation can be re-written as: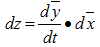 | (3.26) |
But the derivative of the momentum in respect to time represents the force acting on particle. This kind of force is commonly called pure force. Now we re-write (3.26) using SI units: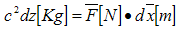 | (3.27) |
It is clear that the right member represents the work done by the pure force 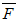 when moving its point of application through
when moving its point of application through 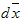 . Because the work equals the increase in particle energy, the equation (2.27) shows the equivalence of mass and energy. The result of the above analyse is the famous Einstein’s formula:
. Because the work equals the increase in particle energy, the equation (2.27) shows the equivalence of mass and energy. The result of the above analyse is the famous Einstein’s formula: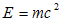 The motion with constant rest mass is produced by a pure force which acts on a moving particle. In this case the equations (3.19) become:
The motion with constant rest mass is produced by a pure force which acts on a moving particle. In this case the equations (3.19) become: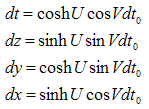 | (3.28) |
Processing equations (3.28) we obtain further the expression of velocity and force.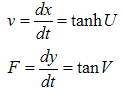 | (3.29) |
For week forces the equations (3.28) contain practically all special relativistic mechanics. If a particle moves non-uniformly under a pure force influence, then the speed of the particle is less than or equal with the speed of light (see the expression of velocity in 3.29).
3.10. The Composition Formula of Forces
The force equation in (3.29) is absolutely new and is a direct result of the H-numbers representation. Let us consider two vigors, V1 and V2, acting simultaneously on a particle. According to relation (3.18) they add together and the resultant force will be,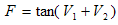 | (3.30) |
But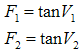 With all that, (3.30) becomes
With all that, (3.30) becomes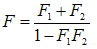 | (3.31) |
This new composition formula has a great theoretical meaning but, for the normal scale of physical reality, it reduces to classical addition of forces. Indeed by translating from GU to SI it obtains: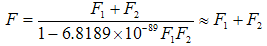
3.11. The Uniform Accelerated Motion
Using the approximations (3.23) and integrating the equations (3.28) it obtains the expressions of all parameters of the moving particle: 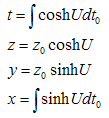 | (3.32) |
In the case of uniform accelerated motion the rapidity is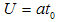 , where a represents the proper acceleration. The expressions of time and space will be:
, where a represents the proper acceleration. The expressions of time and space will be: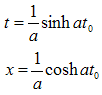 | (3.33) |
We came at the expressions above by conveniently choosing the constants of integration. Thus we arrive to the hyperbolic motion known from special relativity (see Rindler [6]):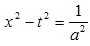 | (3.34) |
The acceleration of the motion is the derivative of velocity in respect to time: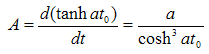 | (3.35) |
3.12. Field Equations in Minkowski Space-Time
Let us consider a function defined on the set E belonging to the 3rd fundamental subspace (see paragraph 2.6):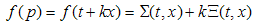 | (3.36) |
We associate with function f a plane vector field, 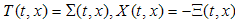 , for every point of the 3rd fundamental subspace. If the function f is monogenic in p, then the following equations are valid:
, for every point of the 3rd fundamental subspace. If the function f is monogenic in p, then the following equations are valid: 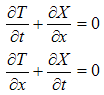 | (3.37) |
If the function f is not monogenic in p, then we can eventually write the equations below: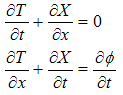 | (3.38) |
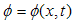 In the Minkowski space-time the spatial component x, is three- dimensional and:
In the Minkowski space-time the spatial component x, is three- dimensional and: 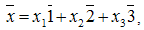 where barred numbers are versors of space coordinates.The Nabla –operator for space variable is:
where barred numbers are versors of space coordinates.The Nabla –operator for space variable is: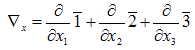 Using the Nabla-operator, the relations (3.38) will become:
Using the Nabla-operator, the relations (3.38) will become: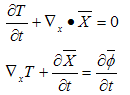 | (3.39) |
where 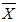 and
and 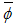 are vector functions. Processing the equations (3.39) it obtains:
are vector functions. Processing the equations (3.39) it obtains: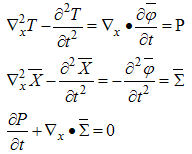 | (3.40) |
These are the general field equations in the Minkowski space. For holomorphic functions, the vector function 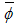 is zero and equations obtained are light-wave equations in vacuum. The field components could be, for example, electromagnetic potentials [12]. Now let us re-write the equations (3.40) using SI units.
is zero and equations obtained are light-wave equations in vacuum. The field components could be, for example, electromagnetic potentials [12]. Now let us re-write the equations (3.40) using SI units.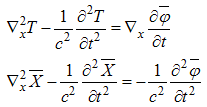 | (3.41) |
If we consider the pair of inhomogeneous wave equations [12] for electromagnetic potentials and identify them with the above ones, then we obtain: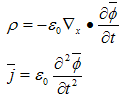 | (3.42) |
More than that, we can write [12] the electric field intensity E, and magnetic induction B as: 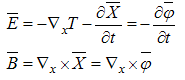 | (3.43) |
We can also verify that the expressions (3.42) and (3.43) lead to the law of charge conservation and to all four Maxwell’s Equations.
4. Physical World and Quantum Behaviour
4.1. Ball in the “Physical World”; Plank’s Constant and Wave Representation
As it was stated in the paragraph 3.2 the physical world is a metric space with the metric defined as follows: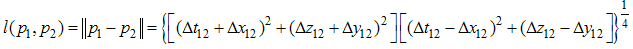 | (4.1) |
Now let us consider a ball [13] centred at a point p0 belonging to the “physical world” and having a radius ρ. The equation of this ball is: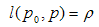 | (4.2) |
This ball is geometrically a super-hyperboloid as we have seen at paragraph 2.11. According to the formula (2.59) the super-volume of this ball is infinite when 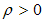 . However, for the case of the light super-hyperboloid (more exactly super-cone) the volume is indeterminate and may have a finite value. By extrapolation we can write:
. However, for the case of the light super-hyperboloid (more exactly super-cone) the volume is indeterminate and may have a finite value. By extrapolation we can write: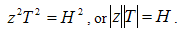 | (4.3) |
Quantities, 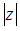 and
and 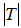 are the absolute values of the mass/momentum and time duration/length of a light particle just emerging from point O. For Euclidean spaces the ball is an n-dimensional sphere and its volume becomes zero when radius goes to zero. These spaces are called continuous. The “physical world” becomes intrinsically a discrete space once we state that the ball’s volume, when radius goes to zero, has a finite and constant value. It can be considered as a network of “super-pixels”, each having the super-volume H2.This hypothesis is sustained by empirical evidence and is expressed by the Max Plank’s quantum theory [14] and the Heisenberg uncertainty principle [15]. The H-numbers model states from beginning that light means moving particles. The idea of particles of light is not new and was developed and sustained by Isaac Newton long time ago.The classic theory of light and Maxwell’s electro-magnetism are treating the light as a wave and this fact is excellently confirmed by various experiments and measurements. Considering this, we may associate a wave, having the frequency
are the absolute values of the mass/momentum and time duration/length of a light particle just emerging from point O. For Euclidean spaces the ball is an n-dimensional sphere and its volume becomes zero when radius goes to zero. These spaces are called continuous. The “physical world” becomes intrinsically a discrete space once we state that the ball’s volume, when radius goes to zero, has a finite and constant value. It can be considered as a network of “super-pixels”, each having the super-volume H2.This hypothesis is sustained by empirical evidence and is expressed by the Max Plank’s quantum theory [14] and the Heisenberg uncertainty principle [15]. The H-numbers model states from beginning that light means moving particles. The idea of particles of light is not new and was developed and sustained by Isaac Newton long time ago.The classic theory of light and Maxwell’s electro-magnetism are treating the light as a wave and this fact is excellently confirmed by various experiments and measurements. Considering this, we may associate a wave, having the frequency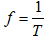 , with the light particle. Thus the equation (4.3) becomes Plank’s equation:
, with the light particle. Thus the equation (4.3) becomes Plank’s equation: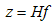 | (4.4) |
The constant H is the Planck’s constant equivalent in GU system. The value of this constant is 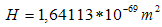 An observer sees a light particle coming from a non-moving source. The corresponding hyper -number representation is:
An observer sees a light particle coming from a non-moving source. The corresponding hyper -number representation is: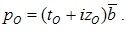 | (4.5) |
The expression 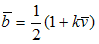 is called vector- base and represents a vector extension of the 0I basic number b (see 2.61). The quantity
is called vector- base and represents a vector extension of the 0I basic number b (see 2.61). The quantity 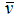 represents a unit vector. The norm of the vector-base is zero if we consider the scalar product for vector components, instead of normal product between real numbers. The reciprocal number
represents a unit vector. The norm of the vector-base is zero if we consider the scalar product for vector components, instead of normal product between real numbers. The reciprocal number 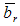 will be written accordingly:
will be written accordingly: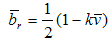 All properties of bases, presented in the paragraph 2.12, remain valid.The associated light wave is represented as a plane wave equation [16]:
All properties of bases, presented in the paragraph 2.12, remain valid.The associated light wave is represented as a plane wave equation [16]: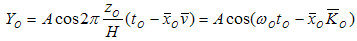 | (4.6) |
The angular frequency is 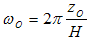 . The vector wave number is
. The vector wave number is 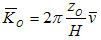 , and
, and 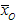 represents the position vector of a point in space.
represents the position vector of a point in space.
4.2. Doppler Shift for Light
If the observer is travelling away from the light-source, then using the generalized pseudo-rotation (see the paragraph 2.6) we can formally write the following equation: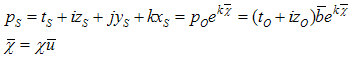 | (4.7) |
Indices O and S mean observer and source. Both 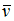 and
and 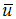 are unit vectors, and their scalar product is
are unit vectors, and their scalar product is 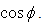 Using the equations (3.13) and changing χ in –χ, we obtain:
Using the equations (3.13) and changing χ in –χ, we obtain: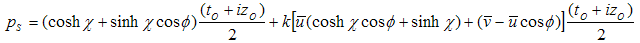 | (4.8) |
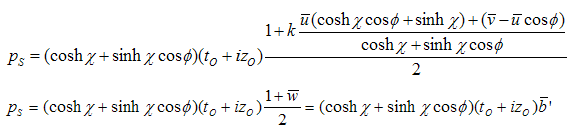 | (4.9) |
The expression 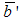 is evidently a vector- base, because
is evidently a vector- base, because 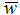 is a unit vector.The relationship between the mass of the particle seen by observer and the mass at the source is:
is a unit vector.The relationship between the mass of the particle seen by observer and the mass at the source is: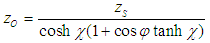 | (4.10) |
Thus the corresponding frequency of the associated wave is: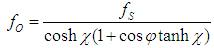 | (4.11) |
The result is the well known relativistic Doppler Effect for light.
4.3. Wave Associated with a Particle
Consider a material point at rest and its corresponding H-number: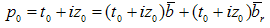 | (4.12) |
This representation is valid for any arbitrary vector base. If the particle is moving with constant velocity, then this is equivalent to a vector pseudo-rotation, and using the procedure exposed in the last paragraph we obtain the expression: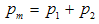 | (4.13) |
The numbers in the right side of (3.13) represents the following two light particles. 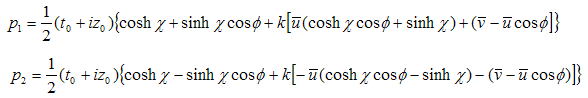 | (4.14) |
As we can see there is a superposition of two light particles moving in symmetric directions. The two corresponding light waves have the angular frequencies: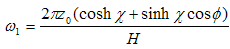 , and respectively,
, and respectively, 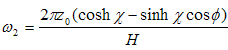 .Their wave numbers are:
.Their wave numbers are: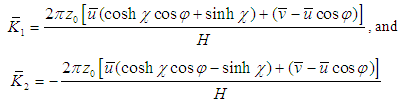 | (4.15) |
The equations of the associated waves, with the presumption that they must have the same amplitude 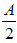 , are written below:
, are written below: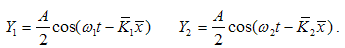 The resulting wave for the moving particle is:
The resulting wave for the moving particle is: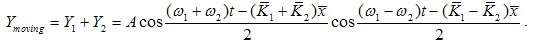 | (4.16) |
But for 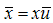 , we get:
, we get: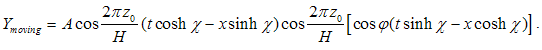 | (4.17) |
Now we should consider that the particle at rest cannot be associated with something moving through the space and so for 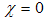 it is required that
it is required that 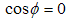 , otherwise the expression above is absurd. Because
, otherwise the expression above is absurd. Because 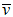 is arbitrary it can be chosen to be perpendicular on
is arbitrary it can be chosen to be perpendicular on 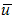 .With all these we finally obtain:
.With all these we finally obtain: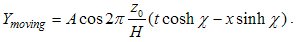 | (4.18) |
Let us have a closer look at this important equation.a. For a particle at rest it becomes: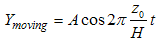 | (4.19) |
This particle is equivalent to a harmonic oscillator having the frequency proportional with the rest mass of the particle.b. For a moving particle the angular frequency and the wave number of the associated wave are 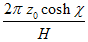 and, respectively
and, respectively 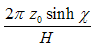 . The frequency and the wave length of this wave are consequently:
. The frequency and the wave length of this wave are consequently: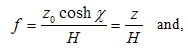 | (4.20) |
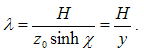 | (4.21) |
The equation (4.21) represents evidently the de Broglie wave length of the matter wave [17]. The phase velocity and the group velocity [18] of the wave are respectively: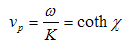 | (4.22) |
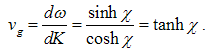 | (4.23) |
In this paragraph has been proved that the matter wave and de Broglie relations are not only the result of the genial, but speculative, hypothesis of Louis de Broglie. The matter wave is the natural consequence of intrinsic properties of the “physical world” and its H-number representation. If we associate a light particle with a light-wave, then a material particle in motion has a corresponding matter wave.
References
| [1] | Vlad L. Negulescu, Hypernumbers and their applications in Mechanics, Romanian Journal of Physics, Volume 42, Nos. 3-4, 1997. |
| [2] | Monogenic functions. E.P. Dolzhenko (originator), Encyclopedia of Mathematics. URL: http://www.encyclopediaofmath.org/index.php?title=Monogenic_function&oldid=15905. |
| [3] | Holomorphic functionhttp://en.wikipedia.org/wiki/Holomorphic_function (accessed May 3 2014). |
| [4] | Conformal map, http://en.wikipedia.org/wiki/Conformal_map (accessed May 3, 2014). |
| [5] | Radius of curvature, http://en.wikipedia.org/wiki/Radius_of_curvature_(mathematics) (accessed May 3, 2014). |
| [6] | Wolfgang Rindler, Introduction to Special Relativity, Oxford University Press, 1982. |
| [7] | Geometrized Units System, http://en.wikipedia.org/wiki/Geometrized_unit_system, (accessed May 3, 2014). |
| [8] | Metric Space, http://en.wikipedia.org/wiki/Metric_space, (accessed May 4, 2014). |
| [9] | World lines in Special Relativity, http://en.wikipedia.org/wiki/World_line, (accessed May 4, 2014). |
| [10] | Rapidity, http://en.wikipedia.org/wiki/Rapidity (accessed May 5, 2014). |
| [11] | Mass in Special Relativity, http://en.wikipedia.org/wiki/Mass_in_special_relativity (accessed May 5, 2014). |
| [12] | R.P. Feynman, R. B. Leighton, M. Sands, The Feynman lectures on physics, 2. Mainly electromagnetism and matter (Reading, Mass., Addison-Wesley,1969). |
| [13] | Ball in general metric spaces, http://en.wikipedia.org/wiki/Ball_(mathematics) (accessed May 5, 2014). |
| [14] | Plank constant http://en.wikipedia.org/wiki/Planck_constant (accessed May 5, 2014). |
| [15] | Uncertainty principle http://en.wikipedia.org/wiki/Uncertainty_principle (accessed May 5, 2014). |
| [16] | Plane wave http://en.wikipedia.org/wiki/Plane_wave (accessed May 25, 2014). |
| [17] | Matter wave http://en.wikipedia.org/wiki/Matter_wave (accessed May 25, 2014). |
| [18] | Waves http://en.wikipedia.org/wiki/Wave#Phase_velocity_ad_group_velocity (accessed May 25, 2014). |

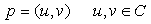
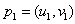 and
and 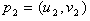 are equal if and only if,
are equal if and only if,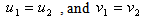
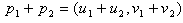
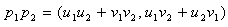
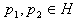 commutativity holds i.e.
commutativity holds i.e.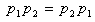 (ii) For all
(ii) For all 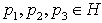 associativity holds i.e.
associativity holds i.e. 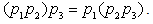 (iii) For all
(iii) For all 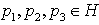 distributivity related to addition (as defined at the point b above) holds, i.e.
distributivity related to addition (as defined at the point b above) holds, i.e.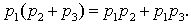 The following fundamental units are denominated: - the number
The following fundamental units are denominated: - the number 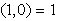 is the real unit;- the number
is the real unit;- the number 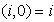 is the imaginary unit;- the number
is the imaginary unit;- the number 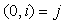 is the co-imaginary unit;- the number
is the co-imaginary unit;- the number 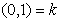 is the co-real unit.Applying the multiplication rule (2.4), we obtain the units multiplication table.
is the co-real unit.Applying the multiplication rule (2.4), we obtain the units multiplication table. 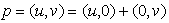
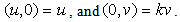 Replacing this into (2.5) we have
Replacing this into (2.5) we have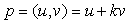
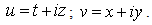
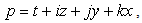
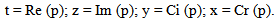 An H-number written as in (2.8) can be represented as a point
An H-number written as in (2.8) can be represented as a point 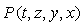 in a four-dimensional space, named hyperspace, using a Cartesian coordinates system with four reciprocally perpendicular axes:- the real axis, with its unit 1,- the imaginary axis, with its unit i,- the co-imaginary, axis with its unit j,- the co-real axis, with its unit k.This point is called the image of the H-number in the hyperspace. Alternatively the image can be the vector OP. Reciprocally, every point P, or vector OP, of the hyperspace has a correspondent H-number which is named the affix of the point P.Between the hyperspace’s points and H-numbers is thus established a one-to-one correspondence. The origin O of the coordinate system represents the image of H-number zero.
in a four-dimensional space, named hyperspace, using a Cartesian coordinates system with four reciprocally perpendicular axes:- the real axis, with its unit 1,- the imaginary axis, with its unit i,- the co-imaginary, axis with its unit j,- the co-real axis, with its unit k.This point is called the image of the H-number in the hyperspace. Alternatively the image can be the vector OP. Reciprocally, every point P, or vector OP, of the hyperspace has a correspondent H-number which is named the affix of the point P.Between the hyperspace’s points and H-numbers is thus established a one-to-one correspondence. The origin O of the coordinate system represents the image of H-number zero.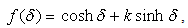
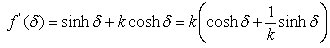 But because k = 1/k, we obtain
But because k = 1/k, we obtain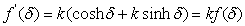
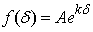
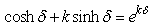
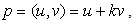 where u, v∈ C, and u2 ≠ v2By definition the complex modulus of p is:
where u, v∈ C, and u2 ≠ v2By definition the complex modulus of p is: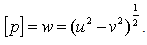
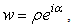
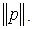 For convenience we write:
For convenience we write: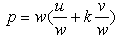
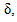 we replace
we replace 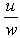 and
and 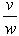 as follows:
as follows: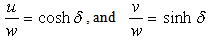
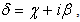 is a complex number, and will be further called Hyperbolic Complex Argument (HCA).Substituting (2.14) and (2.16) into (2.15) one obtains:
is a complex number, and will be further called Hyperbolic Complex Argument (HCA).Substituting (2.14) and (2.16) into (2.15) one obtains: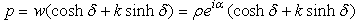
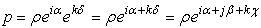
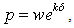 where δ is a complex constant.If w takes all values of the set C, then the image of p is a plane in the hyperspace. When ð varies, the resulting family of planes will generate and cover the hyperspace. The variable ð belongs to the domain in the complex plane (χ, β) bordered by the lines β=0 and
where δ is a complex constant.If w takes all values of the set C, then the image of p is a plane in the hyperspace. When ð varies, the resulting family of planes will generate and cover the hyperspace. The variable ð belongs to the domain in the complex plane (χ, β) bordered by the lines β=0 and 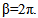 The following expressions represent the transformation from rectangular to exponential coordinates.
The following expressions represent the transformation from rectangular to exponential coordinates.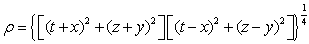
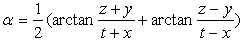
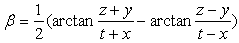
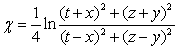
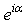 and respectively
and respectively 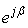 , a
, a 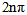 can be added to arguments α and β, where n is an arbitrary integer. If v=0, then the H-number will be reduced to a simple complex number, u, and its complex modulus will be
can be added to arguments α and β, where n is an arbitrary integer. If v=0, then the H-number will be reduced to a simple complex number, u, and its complex modulus will be 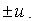 The norm becomes the absolute value of u. Let us make the following notations:
The norm becomes the absolute value of u. Let us make the following notations: 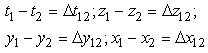 By extension of (2.13) and (2.19) we will define the complex gap, s12, and respectively the norm-distance, l12, between two H-numbers, p1 and p2. Please see 2.23 and 2.24.
By extension of (2.13) and (2.19) we will define the complex gap, s12, and respectively the norm-distance, l12, between two H-numbers, p1 and p2. Please see 2.23 and 2.24.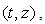 or the 1st fundamental plane;b.
or the 1st fundamental plane;b. 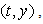 or the 2nd fundamental plane;c.
or the 2nd fundamental plane;c. 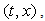 or the 3rd fundamental plane.
or the 3rd fundamental plane.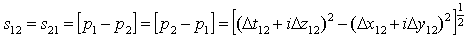
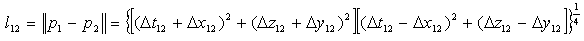

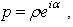 and represents the first fundamental plane for
and represents the first fundamental plane for 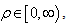 and
and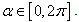 For α=0 and χ=0 we get:
For α=0 and χ=0 we get: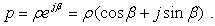 This is the second fundamental plane for
This is the second fundamental plane for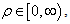 and
and 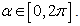 For α=0 and β=0 the expression becomes
For α=0 and β=0 the expression becomes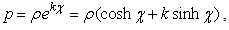 which for
which for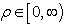 and
and 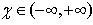 will represents only the wedge I shown in the Figure 1, above. The hyperbola represents the locus of points with ρ constant, belonging to wedge I.Following expressions are valid for H-numbers belonging to others wedges of the plane (t, x).
will represents only the wedge I shown in the Figure 1, above. The hyperbola represents the locus of points with ρ constant, belonging to wedge I.Following expressions are valid for H-numbers belonging to others wedges of the plane (t, x).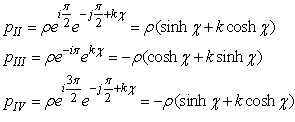
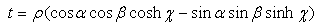
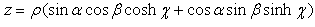
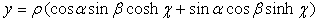
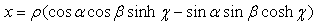
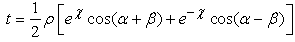
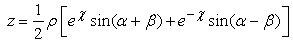
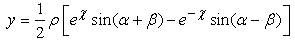
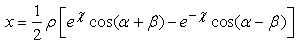
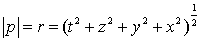
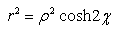
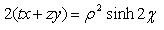
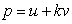 , where
, where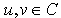 , then its conjugate H-number
, then its conjugate H-number 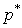 is defined as,
is defined as, 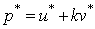 , where
, where 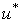 and
and 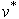 represent the complex conjugates of u and v.
represent the complex conjugates of u and v.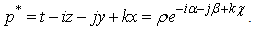
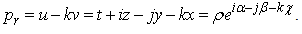
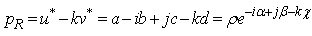
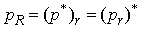
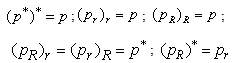
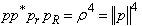
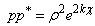
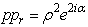
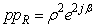
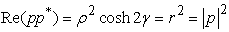
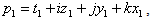 and
and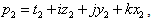 then
then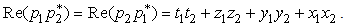
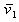 (corresponding number
(corresponding number 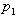 ) and
) and 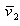 (corresponding number
(corresponding number 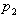 ), can be written as:
), can be written as: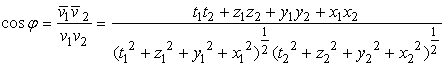
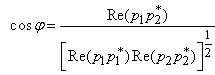
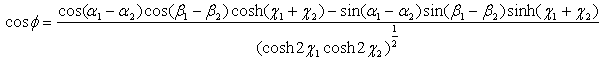
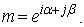
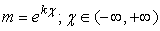
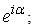 - The 2nd fundamental plane conserves itself after an arbitrary rotation by
- The 2nd fundamental plane conserves itself after an arbitrary rotation by 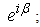 -Each wedge of the 3rd fundamental plane conserves itself after a pseudo-rotation.
-Each wedge of the 3rd fundamental plane conserves itself after a pseudo-rotation. 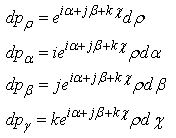
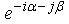 does not change the form of the cell´s image and thus the differential hyper-volume is:
does not change the form of the cell´s image and thus the differential hyper-volume is: 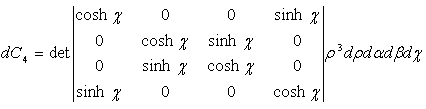
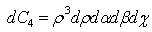
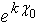 , then a new subset D° will be obtained. The image of D° in the hyperspace is Δ°.Δ and Δ° have the same hyper-volume.The proof is based on the fact that the pseudo-rotation does not change the elementary volume.2. Now we use the expression of the elementary hyper-volume (2.55) and integrating it for
, then a new subset D° will be obtained. The image of D° in the hyperspace is Δ°.Δ and Δ° have the same hyper-volume.The proof is based on the fact that the pseudo-rotation does not change the elementary volume.2. Now we use the expression of the elementary hyper-volume (2.55) and integrating it for 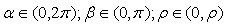 we get:
we get: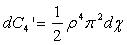
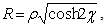 and thus the formula above becomes:
and thus the formula above becomes: 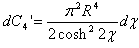 Doing the integral we obtain the volume of the four-dimensional sphere:
Doing the integral we obtain the volume of the four-dimensional sphere: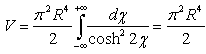
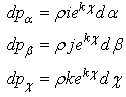 The content of this elementary cell is:
The content of this elementary cell is: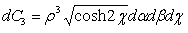
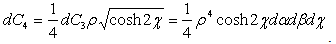 Integrating we obtain the four- dimension volume bordered by the super hyperboloid:
Integrating we obtain the four- dimension volume bordered by the super hyperboloid: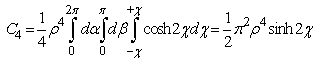
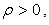 the hyper-volume tends to infinity when
the hyper-volume tends to infinity when 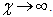 For
For 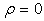 the hyper-volume is indeterminate and can have eventually a finite value.
the hyper-volume is indeterminate and can have eventually a finite value. 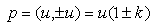
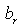 like.It is clear that for any 0I number the complex modulus is zero and the hyperbolic complex argument δ represents the point at infinity. The expression (2.60) shows that every 0I-number can be written as a product of an ordinary complex number with either (1 + k) or (1 - k). Let us define now two particular numbers which are called bases:
like.It is clear that for any 0I number the complex modulus is zero and the hyperbolic complex argument δ represents the point at infinity. The expression (2.60) shows that every 0I-number can be written as a product of an ordinary complex number with either (1 + k) or (1 - k). Let us define now two particular numbers which are called bases: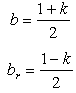
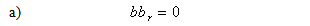
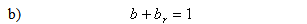
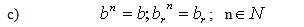
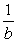 and
and 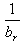 have no mathematical sense in H.e) The following relations are valid:
have no mathematical sense in H.e) The following relations are valid: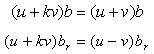
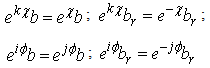
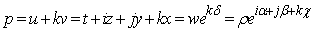
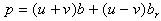
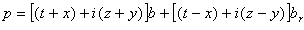
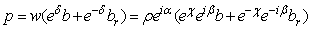
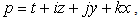 and
and 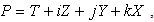 their corresponding elements.Let ΔE and ΔF be images of subsets E and F in the hyperspace.A function, or a map, f associates to each element p∈ E an element P∈ F, and can be written as:
their corresponding elements.Let ΔE and ΔF be images of subsets E and F in the hyperspace.A function, or a map, f associates to each element p∈ E an element P∈ F, and can be written as: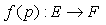
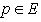 is called the H-number variable. The derivative of the function f (p) in
is called the H-number variable. The derivative of the function f (p) in 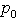 is defined as:
is defined as: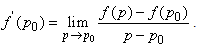 If the derivative at p0 is unique, for all paths in hyperspace, then the function is said to be monogenic at this point (we just extended the definition [2] used for functions of complex variables). A monogenic function in p satisfies at the image point of p, in the four dimensional space, the following equations:
If the derivative at p0 is unique, for all paths in hyperspace, then the function is said to be monogenic at this point (we just extended the definition [2] used for functions of complex variables). A monogenic function in p satisfies at the image point of p, in the four dimensional space, the following equations: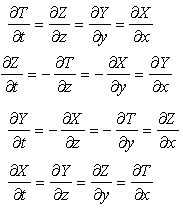
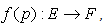 which is monogenic in every point of a subset D⊂ E is said to be monogenic on the subset D or holomorphic [3] on D.The following properties are valid.Property #1.If f(p) is holomorphic on D and its derivative is zero in all points p∈D, then f is a constant on the subset D.Property #2
which is monogenic in every point of a subset D⊂ E is said to be monogenic on the subset D or holomorphic [3] on D.The following properties are valid.Property #1.If f(p) is holomorphic on D and its derivative is zero in all points p∈D, then f is a constant on the subset D.Property #2 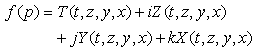 If the function above is holomorphic on D and T, Z, Y, X have their second degree derivatives continuous on the image of D, then the functions T, Z, Y, X satisfy the following system of differential equations:
If the function above is holomorphic on D and T, Z, Y, X have their second degree derivatives continuous on the image of D, then the functions T, Z, Y, X satisfy the following system of differential equations: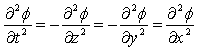
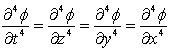
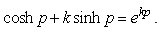
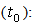
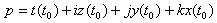
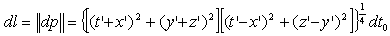
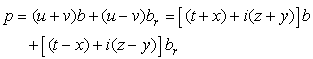
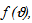 where
where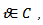 is an analytic one, then:
is an analytic one, then: 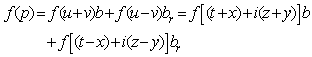
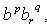 where
where 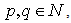 are zero. The above theorem reduces the study of functions with the H-number variable to the ordinary case of functions of complex variable.Now let us write:
are zero. The above theorem reduces the study of functions with the H-number variable to the ordinary case of functions of complex variable.Now let us write: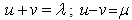
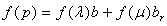
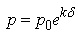
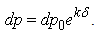
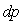 and
and 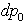 have the same complex modulus. We will say that the mapping p0 →p, performed by (2.82), is conservative. In general a conservative map fulfils the equation (2.83) i.e. it conserves the differential complex modulus. The HCA, δ is no more a constant but a holomorphic function of a complex variable p0.A conservative map transforms a domain belonging to complex plane C into a surface Σ in hyperspace. Its corresponding equation is:
have the same complex modulus. We will say that the mapping p0 →p, performed by (2.82), is conservative. In general a conservative map fulfils the equation (2.83) i.e. it conserves the differential complex modulus. The HCA, δ is no more a constant but a holomorphic function of a complex variable p0.A conservative map transforms a domain belonging to complex plane C into a surface Σ in hyperspace. Its corresponding equation is: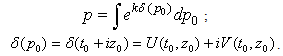
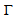 on the surface Σ. In this case t0 is the arc norm- length of the curve
on the surface Σ. In this case t0 is the arc norm- length of the curve 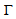 , i.e. this curve is parameterized by its arc norm- length (see 2.77). The complex curvature of the surface Σ is defined as:
, i.e. this curve is parameterized by its arc norm- length (see 2.77). The complex curvature of the surface Σ is defined as: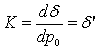
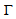 as defined above has an “arc norm- length”-curvature:
as defined above has an “arc norm- length”-curvature: 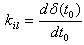
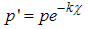
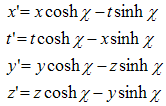
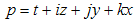
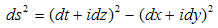
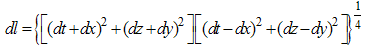
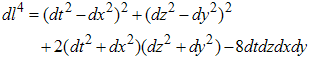
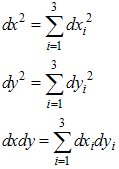
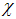 represents the relative rapidity [10] of the coordinate system S’ with respect with the old one S. The velocity of S’ relative to S has the expression:
represents the relative rapidity [10] of the coordinate system S’ with respect with the old one S. The velocity of S’ relative to S has the expression: 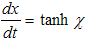
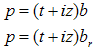 The real, physically observable photon must have a non-zero mass/ momentum z, otherwise it is elusive. The evolution line of a photon will be also named light-path. Once this correspondence has been stated, the theorem 2.3 can be reformulated as follows:Any coordinates transformation performed by a holomorphic function will transform a light-path into another light-path.This fundamental theorem represents a generalisation of the Einstein's law of light propagation.An equivalent formulation of the above theorem is: the speed of light is an invariant (1 in GU system) for any such coordinates transformation.
The real, physically observable photon must have a non-zero mass/ momentum z, otherwise it is elusive. The evolution line of a photon will be also named light-path. Once this correspondence has been stated, the theorem 2.3 can be reformulated as follows:Any coordinates transformation performed by a holomorphic function will transform a light-path into another light-path.This fundamental theorem represents a generalisation of the Einstein's law of light propagation.An equivalent formulation of the above theorem is: the speed of light is an invariant (1 in GU system) for any such coordinates transformation.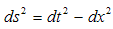
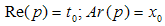
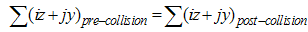
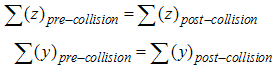
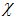 , y and x are vectors, should be considered that the pseudo-rotation acts on t, z and only on the components of x and y parallel to the vector representing the anti-real argument:
, y and x are vectors, should be considered that the pseudo-rotation acts on t, z and only on the components of x and y parallel to the vector representing the anti-real argument: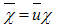
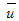 denotes a unit vector and
denotes a unit vector and 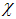 represents the magnitude of
represents the magnitude of 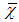 . Thus the general pseudo-rotation transformation equations are:
. Thus the general pseudo-rotation transformation equations are: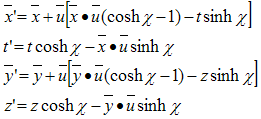
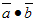 represents the scalar products of two arbitrary vectors. The formula of velocity’s transformation can be obtained by differentiation:
represents the scalar products of two arbitrary vectors. The formula of velocity’s transformation can be obtained by differentiation: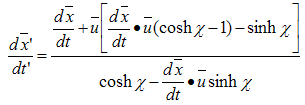
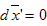 , one obtains the velocity of S’ relative to S:
, one obtains the velocity of S’ relative to S: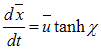
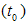 . The mass of the particle represents evidently the rest mass (z0). The observer records only these two parameters and the particle's evline is expressed by:
. The mass of the particle represents evidently the rest mass (z0). The observer records only these two parameters and the particle's evline is expressed by: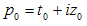
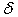 is an analytic function expressed as in the equation (2.84):
is an analytic function expressed as in the equation (2.84):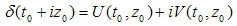
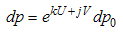
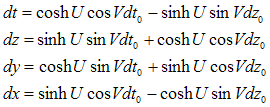
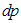 and
and 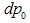 have the same complex modulus and thus:
have the same complex modulus and thus: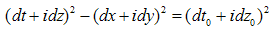
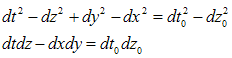
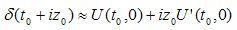
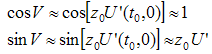
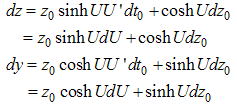
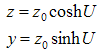
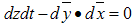 For convenience this equation can be re-written as:
For convenience this equation can be re-written as: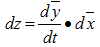
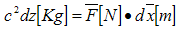
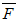 when moving its point of application through
when moving its point of application through 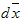 . Because the work equals the increase in particle energy, the equation (2.27) shows the equivalence of mass and energy. The result of the above analyse is the famous Einstein’s formula:
. Because the work equals the increase in particle energy, the equation (2.27) shows the equivalence of mass and energy. The result of the above analyse is the famous Einstein’s formula: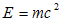 The motion with constant rest mass is produced by a pure force which acts on a moving particle. In this case the equations (3.19) become:
The motion with constant rest mass is produced by a pure force which acts on a moving particle. In this case the equations (3.19) become: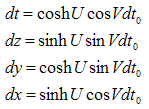
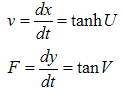
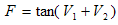
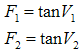 With all that, (3.30) becomes
With all that, (3.30) becomes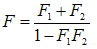
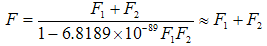
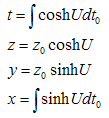
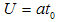 , where a represents the proper acceleration. The expressions of time and space will be:
, where a represents the proper acceleration. The expressions of time and space will be: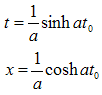
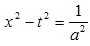
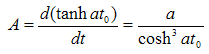
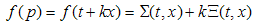
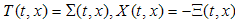 , for every point of the 3rd fundamental subspace. If the function f is monogenic in p, then the following equations are valid:
, for every point of the 3rd fundamental subspace. If the function f is monogenic in p, then the following equations are valid: 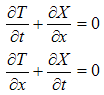
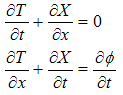
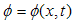 In the Minkowski space-time the spatial component x, is three- dimensional and:
In the Minkowski space-time the spatial component x, is three- dimensional and: 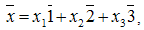 where barred numbers are versors of space coordinates.The Nabla –operator for space variable is:
where barred numbers are versors of space coordinates.The Nabla –operator for space variable is: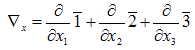 Using the Nabla-operator, the relations (3.38) will become:
Using the Nabla-operator, the relations (3.38) will become: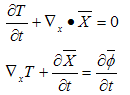
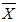 and
and 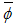 are vector functions. Processing the equations (3.39) it obtains:
are vector functions. Processing the equations (3.39) it obtains: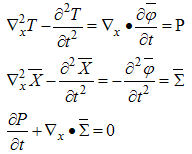
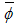 is zero and equations obtained are light-wave equations in vacuum. The field components could be, for example, electromagnetic potentials [12]. Now let us re-write the equations (3.40) using SI units.
is zero and equations obtained are light-wave equations in vacuum. The field components could be, for example, electromagnetic potentials [12]. Now let us re-write the equations (3.40) using SI units.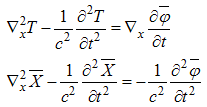
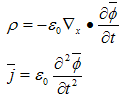
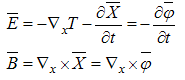
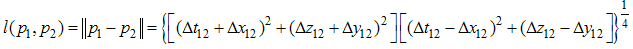
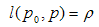
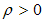 . However, for the case of the light super-hyperboloid (more exactly super-cone) the volume is indeterminate and may have a finite value. By extrapolation we can write:
. However, for the case of the light super-hyperboloid (more exactly super-cone) the volume is indeterminate and may have a finite value. By extrapolation we can write: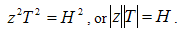
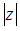 and
and 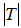 are the absolute values of the mass/momentum and time duration/length of a light particle just emerging from point O. For Euclidean spaces the ball is an n-dimensional sphere and its volume becomes zero when radius goes to zero. These spaces are called continuous. The “physical world” becomes intrinsically a discrete space once we state that the ball’s volume, when radius goes to zero, has a finite and constant value. It can be considered as a network of “super-pixels”, each having the super-volume H2.This hypothesis is sustained by empirical evidence and is expressed by the Max Plank’s quantum theory [14] and the Heisenberg uncertainty principle [15]. The H-numbers model states from beginning that light means moving particles. The idea of particles of light is not new and was developed and sustained by Isaac Newton long time ago.The classic theory of light and Maxwell’s electro-magnetism are treating the light as a wave and this fact is excellently confirmed by various experiments and measurements. Considering this, we may associate a wave, having the frequency
are the absolute values of the mass/momentum and time duration/length of a light particle just emerging from point O. For Euclidean spaces the ball is an n-dimensional sphere and its volume becomes zero when radius goes to zero. These spaces are called continuous. The “physical world” becomes intrinsically a discrete space once we state that the ball’s volume, when radius goes to zero, has a finite and constant value. It can be considered as a network of “super-pixels”, each having the super-volume H2.This hypothesis is sustained by empirical evidence and is expressed by the Max Plank’s quantum theory [14] and the Heisenberg uncertainty principle [15]. The H-numbers model states from beginning that light means moving particles. The idea of particles of light is not new and was developed and sustained by Isaac Newton long time ago.The classic theory of light and Maxwell’s electro-magnetism are treating the light as a wave and this fact is excellently confirmed by various experiments and measurements. Considering this, we may associate a wave, having the frequency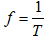 , with the light particle. Thus the equation (4.3) becomes Plank’s equation:
, with the light particle. Thus the equation (4.3) becomes Plank’s equation: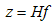
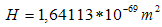 An observer sees a light particle coming from a non-moving source. The corresponding hyper -number representation is:
An observer sees a light particle coming from a non-moving source. The corresponding hyper -number representation is: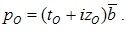
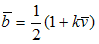 is called vector- base and represents a vector extension of the 0I basic number b (see 2.61). The quantity
is called vector- base and represents a vector extension of the 0I basic number b (see 2.61). The quantity 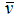 represents a unit vector. The norm of the vector-base is zero if we consider the scalar product for vector components, instead of normal product between real numbers. The reciprocal number
represents a unit vector. The norm of the vector-base is zero if we consider the scalar product for vector components, instead of normal product between real numbers. The reciprocal number 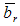 will be written accordingly:
will be written accordingly: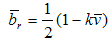 All properties of bases, presented in the paragraph 2.12, remain valid.The associated light wave is represented as a plane wave equation [16]:
All properties of bases, presented in the paragraph 2.12, remain valid.The associated light wave is represented as a plane wave equation [16]: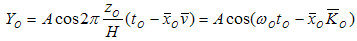
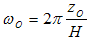 . The vector wave number is
. The vector wave number is 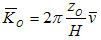 , and
, and 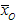 represents the position vector of a point in space.
represents the position vector of a point in space.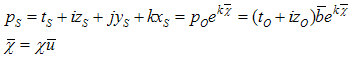
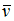 and
and 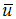 are unit vectors, and their scalar product is
are unit vectors, and their scalar product is 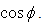 Using the equations (3.13) and changing χ in –χ, we obtain:
Using the equations (3.13) and changing χ in –χ, we obtain: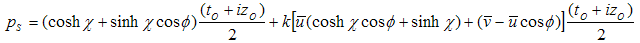
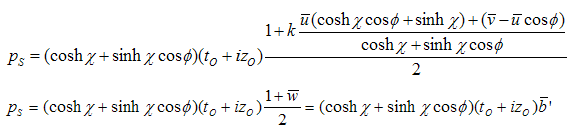
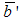 is evidently a vector- base, because
is evidently a vector- base, because 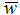 is a unit vector.The relationship between the mass of the particle seen by observer and the mass at the source is:
is a unit vector.The relationship between the mass of the particle seen by observer and the mass at the source is: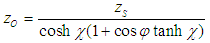
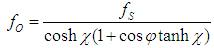
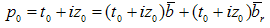
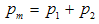
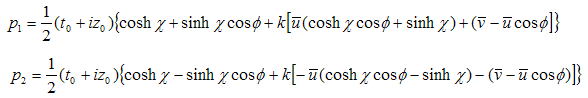
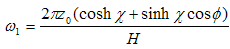 , and respectively,
, and respectively, 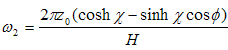 .Their wave numbers are:
.Their wave numbers are: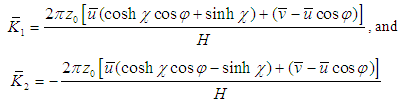
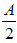 , are written below:
, are written below: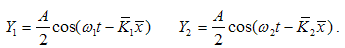 The resulting wave for the moving particle is:
The resulting wave for the moving particle is: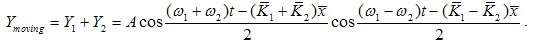
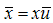 , we get:
, we get: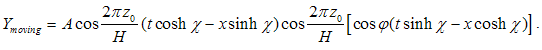
 it is required that
it is required that 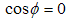 , otherwise the expression above is absurd. Because
, otherwise the expression above is absurd. Because 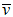 is arbitrary it can be chosen to be perpendicular on
is arbitrary it can be chosen to be perpendicular on 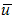 .With all these we finally obtain:
.With all these we finally obtain: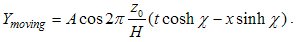
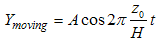
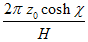 and, respectively
and, respectively 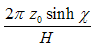 . The frequency and the wave length of this wave are consequently:
. The frequency and the wave length of this wave are consequently: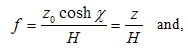
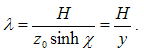
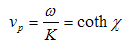
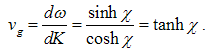
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
