Nelson O. Nenuwe 1, Famous Akpojotor 2
1Department of Physics, Federal University of Petroleum Resources, Effurun, Nigeria
2Department of Physics, University of Benin, Benin City, Nigeria
Correspondence to: Nelson O. Nenuwe , Department of Physics, Federal University of Petroleum Resources, Effurun, Nigeria.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The power-law dependence of correlation functions at low energies is what clearly distinguishes the Tomonaga-Luttinger (TL) liquid and the Fermi liquid (FL). The correlation function critical exponent for the FL is usually fixed to an integer, while that of the TL liquid varies continuously. We calculate the nature of power-law dependence in the charge, spin and electron correlation functions for the TL liquid at both zero and small magnetic fields. In particular, our approach centres on the Bethe Ansatz and conformal field theory (CFT). This is important since the concept of CFT relates critical exponents of various correlation functions with the finite-size corrections to the energy spectrum. Our findings show that increase in the particle density nc, and external magnetic field B, increases the value of the critical exponents while increase in the interaction strength u, decreases the value of the critical exponents.
Keywords:
Tomonaga-Luttinger liquid, Power-law, Correlation function, Conformal field theory
Cite this paper: Nelson O. Nenuwe , Famous Akpojotor , Power-Law Dependence of Correlaration Functions in the Tomonaga-Luttinger Liquid, International Journal of Theoretical and Mathematical Physics, Vol. 5 No. 1, 2015, pp. 8-15. doi: 10.5923/j.ijtmp.20150501.02.
1. Introduction
In condensed matter physics, the Tomonaga-Luttinger (TL) liquid [1-3] has received huge interest because of its role in replacing the properties of the Fermi liquid (FL) in one-dimension. The most significant behaviour of the TL liquid is the unusual power-law dependence [4] appearing in various correlation functions at low energies. For instance, the charge, spin and electron correlation functions between two positions 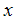 and
and 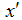 shows a power-law dependence in the long-distance region, where the critical exponent changes continuously depending on the strength of interaction between particles and spin dimension. This is quite different from the FL behaviour where the critical exponent is fixed to an integer. The typical FL theory in based on a quasi-particle picture breaks down in one dimension due to large quantum fluctuations, and therefore the TL liquid governed by collective excitations of spin and charge takes over the role of FL in one dimension [5]. The charge and spin fluctuations scatter with different velocities and the correlations between excitations are unusual and appears as interaction dependent power-laws in physical quantities [6]. The concept of TL liquid coined by Haldane [7] to describe general low-energy properties of gapless one-dimensional (1D) systems and to emphasize that an asymptotic description can be based on the TL liquid in much the same way as the FL theory in three-dimension is based on the Fermi gas, makes it clear that the TL liquid properties governs a large class of universal lattice models in one dimension, such as the 1D Hubbard model and t-J model [8].Conformal field theory which has important applications in string theory, statistical mechanics and condensed matter physics provides a general method for calculating correlation functions of interest. It relates the critical exponents of the correlation functions with finite-size corrections to the energy spectrum [9]. The dressed charge matrix is the basic tool used to determine the critical exponents from the finite-size correction. In this study, the CFT technique will be used to calculate the power-law dependence of the correlation functions and evaluate the nature of the critical exponents of the highly correlated 1D repulsive Hubbard model, as an example of a TL liquid at zero field and small magnetic field.
shows a power-law dependence in the long-distance region, where the critical exponent changes continuously depending on the strength of interaction between particles and spin dimension. This is quite different from the FL behaviour where the critical exponent is fixed to an integer. The typical FL theory in based on a quasi-particle picture breaks down in one dimension due to large quantum fluctuations, and therefore the TL liquid governed by collective excitations of spin and charge takes over the role of FL in one dimension [5]. The charge and spin fluctuations scatter with different velocities and the correlations between excitations are unusual and appears as interaction dependent power-laws in physical quantities [6]. The concept of TL liquid coined by Haldane [7] to describe general low-energy properties of gapless one-dimensional (1D) systems and to emphasize that an asymptotic description can be based on the TL liquid in much the same way as the FL theory in three-dimension is based on the Fermi gas, makes it clear that the TL liquid properties governs a large class of universal lattice models in one dimension, such as the 1D Hubbard model and t-J model [8].Conformal field theory which has important applications in string theory, statistical mechanics and condensed matter physics provides a general method for calculating correlation functions of interest. It relates the critical exponents of the correlation functions with finite-size corrections to the energy spectrum [9]. The dressed charge matrix is the basic tool used to determine the critical exponents from the finite-size correction. In this study, the CFT technique will be used to calculate the power-law dependence of the correlation functions and evaluate the nature of the critical exponents of the highly correlated 1D repulsive Hubbard model, as an example of a TL liquid at zero field and small magnetic field.
2. Finite-Size Scaling in Conformal Field Theory
The conformal dimensions will be obtained from the Hamiltonian of the 1D Hubbard model, defined by [10]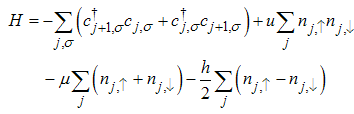 | (1) |
Where 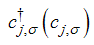 | (2) |
is creation (annihilation) operator with electron spin σ at site j and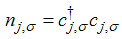 | (3) |
is the number operator. u is the on-site Coulomb repulsion, μ is the chemical potential and h is the external magnetic field. The hopping integral t=1. Eqn. (1) has been solved exactly using the Bethe Ansatz by Lieb and Wu [11]. The wave function of the chain with sites can be written in terms of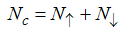 | (4) |
electrons, where N↑ and N↓ are the number of electrons with spin up and down, and Ns =N↓ down spins are characterized by the momenta kj of holons and rapidities λα of spinons. This leads to the Bethe Ansatz equations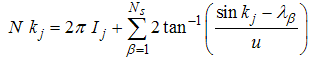 | (5) |
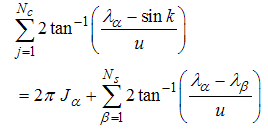 | (6) |
with quantum number Ij and Jα as integers or half-odd integer, depending on the parities of the numbers of down and up spins, respectively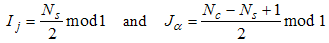 | (7) |
The state corresponding to the solution of Eqns. (5) and (6) has energy and momentum given by [12, 13]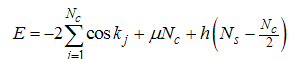 | (8) |
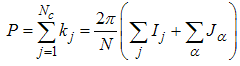 | (9) |
To leading order in 1/N the energy and momentum of the excitations can be written in the form [14]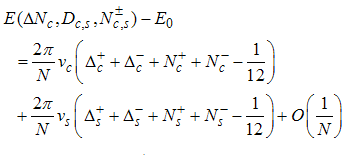 | (10) |
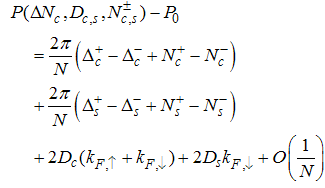 | (11) |
Where the conformal dimensions are given by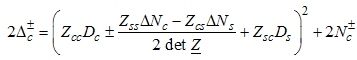 | (12) |
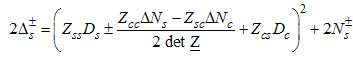 | (13) |
The Dc and Ds takes integer or half-odd integer values and is the dressed charge matrix defined by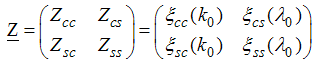 | (14) |
The elements of the dressed charge matrix (14) are given by the coupled integral equations 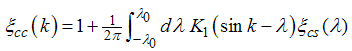 | (15) |
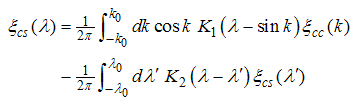 | (16) |
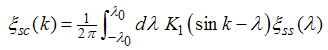 | (17) |
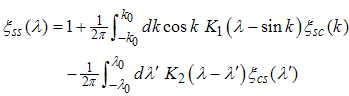 | (18) |
Where the kernel is defined as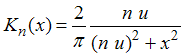 | (19) |
It is well known that the CFT expressions for correlation function of a primary operator [11] contains factors from holons and spinons, given by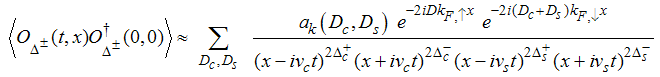 | (20) |
Where ΟΔ± is the field operator, kF,↑ and kF,↓ are the Fermi momenta for electrons with spin up and down, respectively. vc and vs are the Fermi velocities of charge and spin density waves andɑk are constant coefficients.
3. Power-Law Decay of the Correlation Functions
In this section we proceed to calculate the charge, spin and electron correlation functions at zero magnetic field and small magnetic field for the 1D Hubbard model.
3.1. Zero Magnetic Field
At zero magnetic field the ground state of the Hubbard model is antiferromagnetic, and the dressed charge matrix takes the form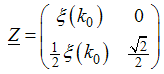 | (21) |
and 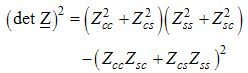 | (22) |
Using Eqn. (21) on (22), we obtain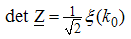 | (23) |
Using Eqn. (21) on Eqns. (12) and (13), we obtain the consequence of the dressed charge matrix on the conformal dimensions as 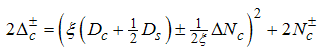 | (24) |
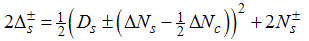 | (25) |
Therefore, the correlation functions are obtained as follows.(i) The power-law decay for the charge density correlatororiginates from the quantum numbers (Dc, Ds) = (0, 1), (1, 0), (1, -1), ΔNc=ΔNs=0 and N±c,s=0. The equivalent conformal dimensions to these set of quantum numbers are obtained as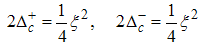 | (26) |
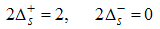 | (27) |
for (Dc, Ds) = (0, 1), with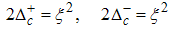 | (28) |
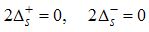 | (29) |
for (Dc, Ds) = (1, 0), and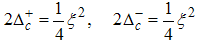 | (30) |
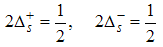 | (31) |
for (Dc, Ds) = (1, -1). Therefore, the correlation function is obtained as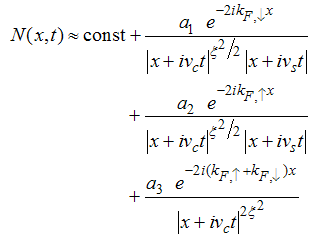 | (32) |
It is well known that at vanishing magnetic field 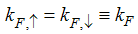 | (33) |
Expressing the critical exponents of the correlator as function of 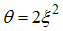 | (34) |
Eqn. (32) becomes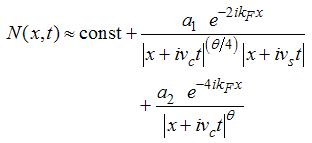 | (35) |
The critical exponent θ changes continuously with change in interaction strength.(ii) The power-law decay for the transverse spin correlatororiginates from the quantum numbers (Dc, Ds) = (1/2, 0), (-3/2, 1), and (-5/2, 1), ΔNc=0, ΔNs=1 and N±c,s=0. The equivalent conformal dimensions are 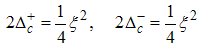 | (36) |
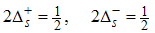 | (37) |
for (Dc, Ds) = (1/2, 0), with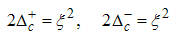 | (38) |
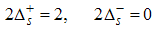 | (39) |
for (Dc, Ds) = (-3/2, 1), and 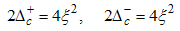 | (40) |
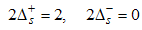 | (41) |
for (Dc, Ds) = (-5/2, 1). Therefore, the spin correlator is then given by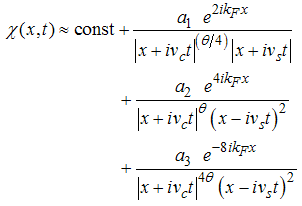 | (42) |
The spin correlator decays in powers of θ and the critical exponent θ changes continuously as the interaction strength u, changes.(iii) Power-law decay for the electron correlator with spin up originates from the quantum numbers (Dc, Ds) = (-1/2, 1/2), (-3/2, 3/2), ΔNc=1, ΔNs=0 and N±c,s=0. The equivalent conformal dimensions are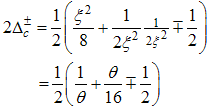 | (43) |
By using 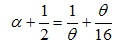 | (44) |
on Eqn. (43), we obtain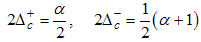 | (45) |
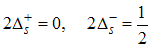 | (46) |
for (Dc, Ds) = (-1/2, 1/2), and for (Dc, Ds) = (-3/2, 3/2), we obtain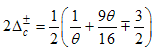 | (47) |
Using 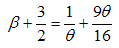 | (48) |
on (47), we obtain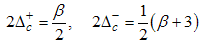 | (49) |
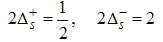 | (50) |
The electron correlation function is then obtained as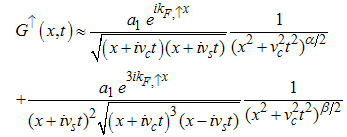 | (51) |
Here the electron correlator decays as functions of α for contributions from kF, ↑ and β for contributions from 3kF, ↑. The critical exponents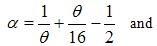 | (52) |
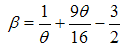 | (53) |
change continuously as θ also changes with change in the interaction strength u.
3.2. The Limit of Small Magnetic Field
Solving the dressed charge matrix Eqns. (15) to (18) for small magnetic field with the Wiener-Hopf technique gives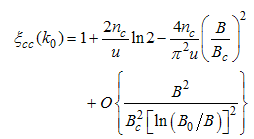 | (54) |
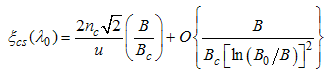 | (55) |
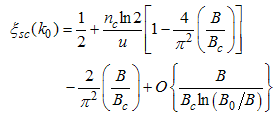 | (56) |
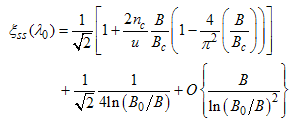 | (57) |
Where B is an external field, Bc is the critical field u is the interacting strength and nc is the particle density.Using Eqns. (54) to (57) on Eqns. (12) and (13), we obtain the magnetic field dependence of the conformal dimensions as 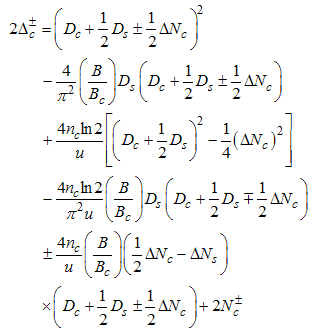 | (58) |
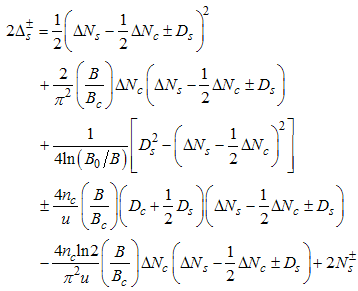 | (59) |
Using Eqn. (58) and (59), we proceed to calculate the power-law dependence for the correlation functions in the presence of small magnetic field.(i) The power-law decay for the charge density correlator. The conformal dimensions here are obtained as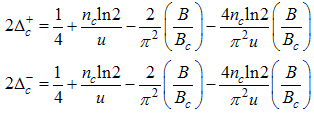 | (60) |
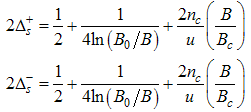 | (61) |
for (Dc, Ds) = (0, 1), with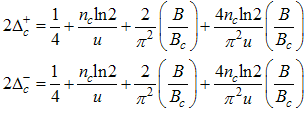 | (62) |
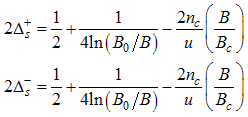 | (63) |
for (Dc, Ds) = (1, -1), and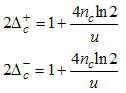 | (64) |
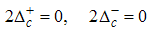 | (65) |
for (Dc, Ds) = (1, 0). The correlation function then decay as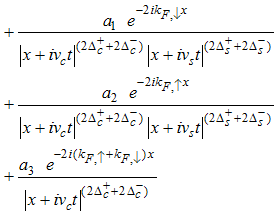 | (66) |
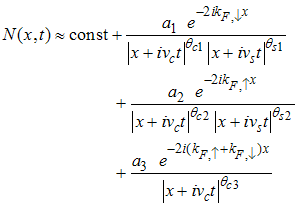 | (67) |
Where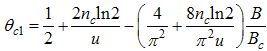 | (68) |
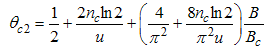 | (69) |
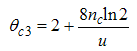 | (70) |
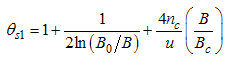 | (71) |
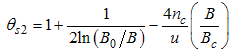 | (72) |
Here, the charge density correlator decays as functions of the critical exponents given in Eqns. (68) to (72).It can be seen that the critical exponents has logarithmic dependence and also varies as functions of interaction strength u, electron density nc and external magnetic field.(ii) The power-law decay for the transverse spin correlator. The equivalent conformal dimensions are 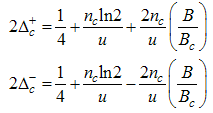 | (73) |
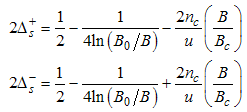 | (74) |
for (Dc, Ds) = (1/2, 0), with 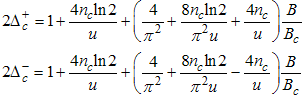 | (75) |
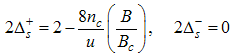 | (76) |
for (Dc, Ds) = (-3/2, 1), and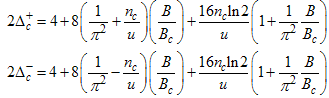 | (77) |
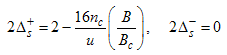 | (78) |
for (Dc, Ds) = (-5/2, 1).Therefore, the transverse spin correlation function is given by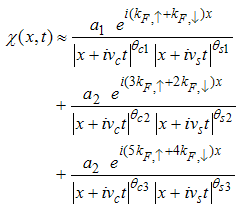 | (79) |
Where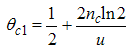 | (80) |
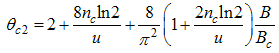 | (81) |
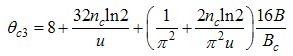 | (82) |
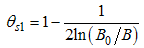 | (83) |
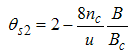 | (84) |
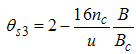 | (85) |
The critical exponents Eqns. (80) to (85) change continuously as functions of interaction strength u, electron density nc, and external magnetic field B. From the critical exponents, it is obvious that the spin correlation function also has logarithmic dependence. (iii) The power-law decay for the electron correlator with spin up. The equivalent conformal dimensions here are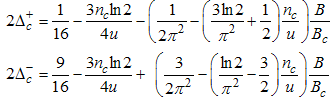 | (86) |
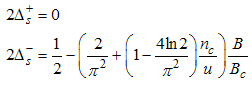 | (87) |
for (Dc, Ds) = (-1/2, 1/2), and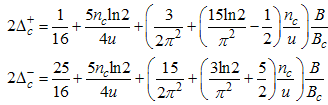 | (88) |
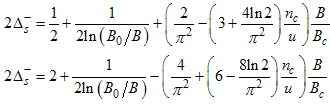 | (89) |
for Dc, Ds) = (-3/2, 3/2).Then, the electron correlation function 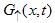 is given by
is given by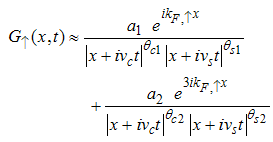 | (90) |
Where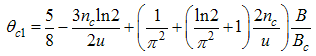 | (91) |
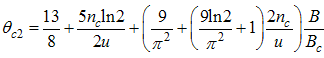 | (92) |
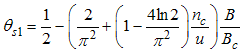 | (93) |
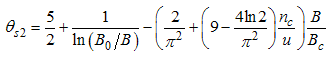 | (94) |
The electron correlator, 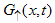 decays in powers of the critical exponents Eqns. (91) to (94), which varies continuously with change in interaction strength u, electron density nc, and external magnetic field.
decays in powers of the critical exponents Eqns. (91) to (94), which varies continuously with change in interaction strength u, electron density nc, and external magnetic field.
4. Conclusions
We have calculated the nature of power-law dependence of correlation functions for the TL liquid and discovered that the correlation functions decay as powers of varying critical exponents. It is generally believed that, the physics of power-law behaviour of most correlated 1D electron systems, differentiates the TL liquid from the three dimensional electron systems governed by the FL. For the 1D Hubbard model (Section 3), at zero magnetic field, the charge, spin and electron correlation functions decay as power of the critical exponent 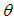 , which varies with varying interaction strength u, while in the limit of small magnetic field, the charge, spin and electron correlation functions decay as powers of the critical exponents given by Eqns. (68) to (72), Eqns. (80) to (85) and Eqns. (91) to (94), respectively. The values of the critical exponents for small magnetic field, increase with increasing particle density nc, and magnetic field B, while increasing the interaction strength u, decreases the value of the critical exponents. Therefore, it is expected that our calculation will provide very useful insights in investigating how power-law behaviour affects other physical properties of interest in TL liquids.
, which varies with varying interaction strength u, while in the limit of small magnetic field, the charge, spin and electron correlation functions decay as powers of the critical exponents given by Eqns. (68) to (72), Eqns. (80) to (85) and Eqns. (91) to (94), respectively. The values of the critical exponents for small magnetic field, increase with increasing particle density nc, and magnetic field B, while increasing the interaction strength u, decreases the value of the critical exponents. Therefore, it is expected that our calculation will provide very useful insights in investigating how power-law behaviour affects other physical properties of interest in TL liquids.
References
| [1] | Luttinger, J. M. (1963). An exactly soluble model of a many fermion system. J. Math. Phys.4 (9), 1154-1162. |
| [2] | Mattis, D.C., and Lieb, E.H. (1965).Exact solution of a Many-Fermion Systems and its Associated Boson Field. J. Math. Phys.6 (2), 304-312. |
| [3] | Nenuwe, O.N., Babalola, M.E. and Idiodi J.O.A. (2012). The Tomonaga model. J. NAMP 20, 205-212. |
| [4] | Stanley, H.E., Buldyrev, S.V., Goldberger, A.L., Havlin, S., Peng, C.K. and Simons, M. (1993). Long-range power-law correlation in condensed matter physics and biophysics. Physica A 200, 4-24. |
| [5] | Kawakami, N. (2007). Tomonaga theory for collective fermions: basic concept of one dimensional correlated electrons. Prog. Theor. Phys. Suppl. (170), 185-197. |
| [6] | Voit, J. (1995). One-dimensional Fermi liquids. Reports on Progress in Physics,58(9), 977. |
| [7] | Haldane, F.D.M. (1981). 'Luttinger liquid theory' of one-dimensional quantum fluids. I. Properties of the Luttinger model and their extension to the general 1D interacting spinless Fermi gas. Journal of Physics C: Solid State Physics, 14(19), 2585. |
| [8] | Sirker, J. (2012). The Luttinger liquid and integrable models. International Journal of Modern Physics B, 26(22). |
| [9] | Belavin, A.A., Polyakov, A.M., and Zamolodchikov, A.B. (1984). Infinite conformal symmetry in two-dimensional quantum field theory. Nucl. Phys. B241, 333-380. |
| [10] | Penc, K. and Solyom, J. (1993). One dimensional Hubbard model in a magnetic field and the multicomponent Tomonaga-Luttinger model. Phys. Rev. B 47, 6273-6292. |
| [11] | Lieb, E.H., and Wu, F.Y. (1968). Absence of Mott Transition in an Exact Solution of the Short-Range, One-Band Model in One Dimension. Phys. Rev. Lett.20 (25), 1445-1448. |
| [12] | Kawakami, N., and Yang, S-K. (1992).Conformal field theory approach to one dimensional quantum liquids. Prog. Theor. Phys. Suppl. No.107, p59-75. |
| [13] | Frahm, H. and Korepin, V.E. (1990).Critical Exponents for the One-Dimensional Hubbard Model. Phys. Rev. B42 (16), 10553-10565. |
| [14] | Woynarovich, F. (1989). Finite-size effects in a non-half-filled Hubbard chain. J. Phys. A22, 4243-4256. |
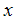 and
and 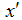 shows a power-law dependence in the long-distance region, where the critical exponent changes continuously depending on the strength of interaction between particles and spin dimension. This is quite different from the FL behaviour where the critical exponent is fixed to an integer. The typical FL theory in based on a quasi-particle picture breaks down in one dimension due to large quantum fluctuations, and therefore the TL liquid governed by collective excitations of spin and charge takes over the role of FL in one dimension [5]. The charge and spin fluctuations scatter with different velocities and the correlations between excitations are unusual and appears as interaction dependent power-laws in physical quantities [6]. The concept of TL liquid coined by Haldane [7] to describe general low-energy properties of gapless one-dimensional (1D) systems and to emphasize that an asymptotic description can be based on the TL liquid in much the same way as the FL theory in three-dimension is based on the Fermi gas, makes it clear that the TL liquid properties governs a large class of universal lattice models in one dimension, such as the 1D Hubbard model and t-J model [8].Conformal field theory which has important applications in string theory, statistical mechanics and condensed matter physics provides a general method for calculating correlation functions of interest. It relates the critical exponents of the correlation functions with finite-size corrections to the energy spectrum [9]. The dressed charge matrix is the basic tool used to determine the critical exponents from the finite-size correction. In this study, the CFT technique will be used to calculate the power-law dependence of the correlation functions and evaluate the nature of the critical exponents of the highly correlated 1D repulsive Hubbard model, as an example of a TL liquid at zero field and small magnetic field.
shows a power-law dependence in the long-distance region, where the critical exponent changes continuously depending on the strength of interaction between particles and spin dimension. This is quite different from the FL behaviour where the critical exponent is fixed to an integer. The typical FL theory in based on a quasi-particle picture breaks down in one dimension due to large quantum fluctuations, and therefore the TL liquid governed by collective excitations of spin and charge takes over the role of FL in one dimension [5]. The charge and spin fluctuations scatter with different velocities and the correlations between excitations are unusual and appears as interaction dependent power-laws in physical quantities [6]. The concept of TL liquid coined by Haldane [7] to describe general low-energy properties of gapless one-dimensional (1D) systems and to emphasize that an asymptotic description can be based on the TL liquid in much the same way as the FL theory in three-dimension is based on the Fermi gas, makes it clear that the TL liquid properties governs a large class of universal lattice models in one dimension, such as the 1D Hubbard model and t-J model [8].Conformal field theory which has important applications in string theory, statistical mechanics and condensed matter physics provides a general method for calculating correlation functions of interest. It relates the critical exponents of the correlation functions with finite-size corrections to the energy spectrum [9]. The dressed charge matrix is the basic tool used to determine the critical exponents from the finite-size correction. In this study, the CFT technique will be used to calculate the power-law dependence of the correlation functions and evaluate the nature of the critical exponents of the highly correlated 1D repulsive Hubbard model, as an example of a TL liquid at zero field and small magnetic field. 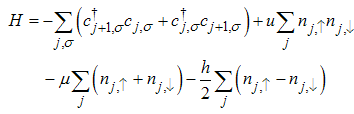
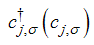
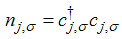
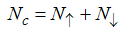
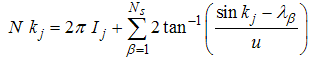
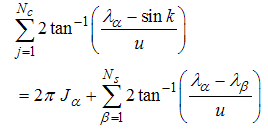
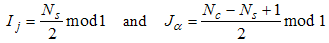
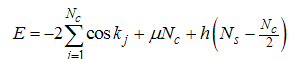
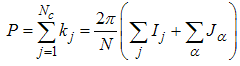
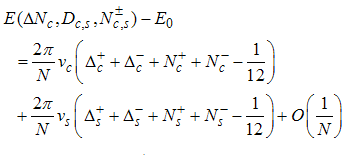
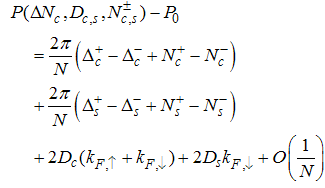
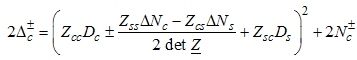
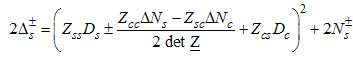
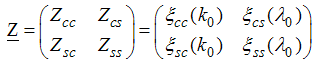
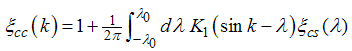
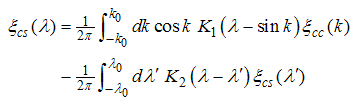
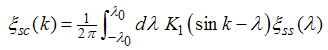
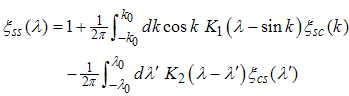
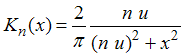
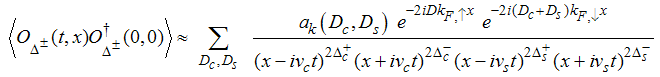
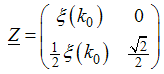
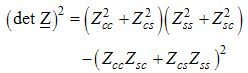
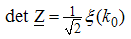
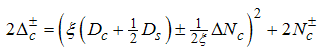
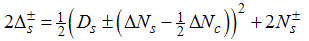
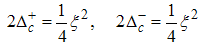
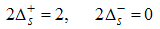
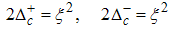
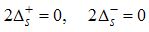
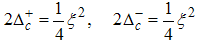
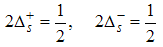
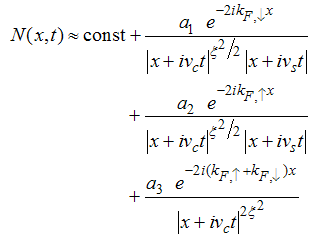
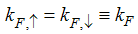
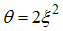
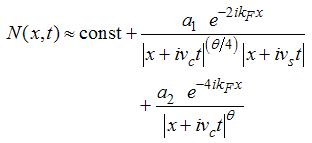
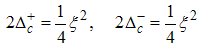
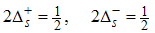
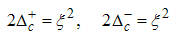
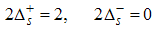
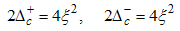
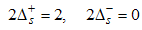
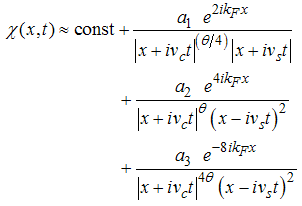
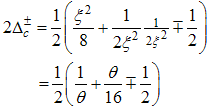
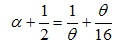
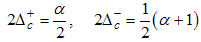
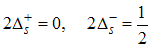
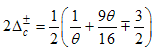
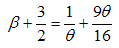
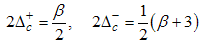
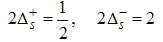
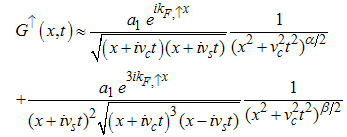
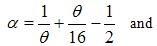
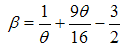
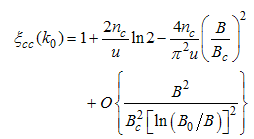
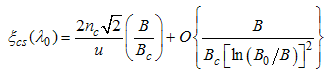
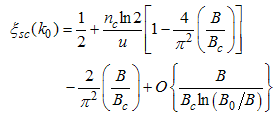
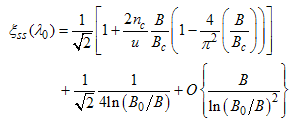
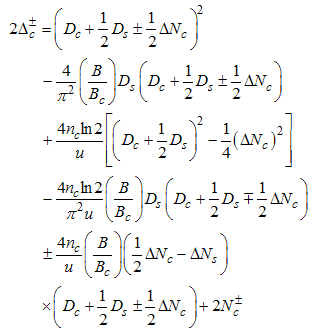
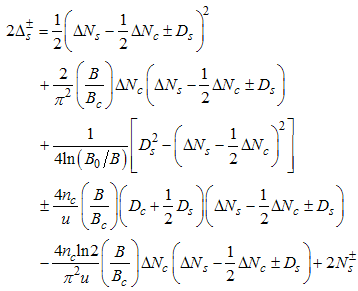
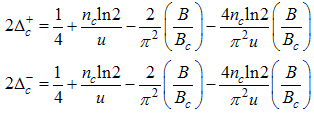
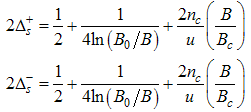
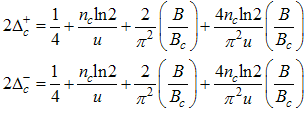
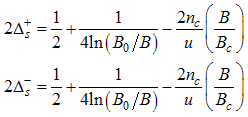
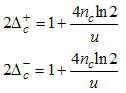
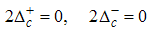
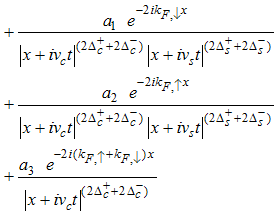
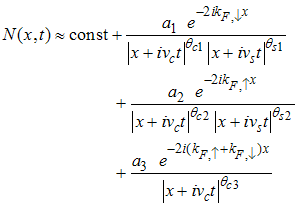
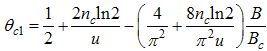
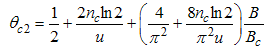
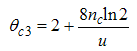
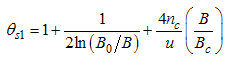
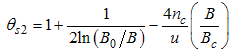
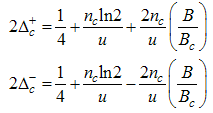
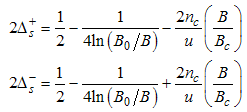
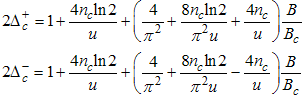
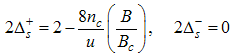
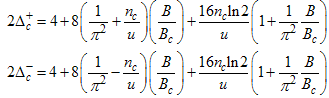
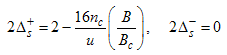
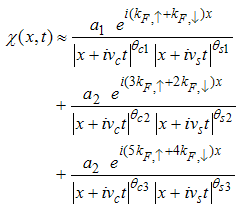
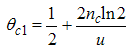
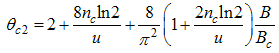
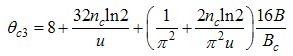
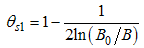
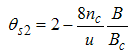
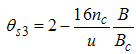
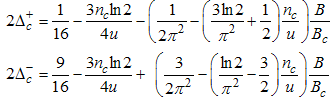
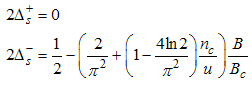
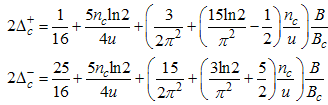
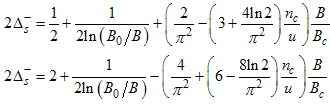
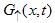 is given by
is given by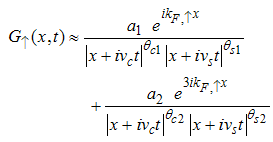
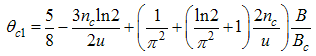
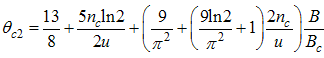
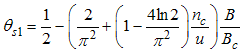
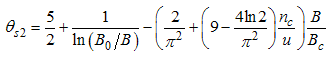
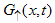 decays in powers of the critical exponents Eqns. (91) to (94), which varies continuously with change in interaction strength u, electron density nc, and external magnetic field.
decays in powers of the critical exponents Eqns. (91) to (94), which varies continuously with change in interaction strength u, electron density nc, and external magnetic field.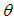 , which varies with varying interaction strength u, while in the limit of small magnetic field, the charge, spin and electron correlation functions decay as powers of the critical exponents given by Eqns. (68) to (72), Eqns. (80) to (85) and Eqns. (91) to (94), respectively. The values of the critical exponents for small magnetic field, increase with increasing particle density nc, and magnetic field B, while increasing the interaction strength u, decreases the value of the critical exponents. Therefore, it is expected that our calculation will provide very useful insights in investigating how power-law behaviour affects other physical properties of interest in TL liquids.
, which varies with varying interaction strength u, while in the limit of small magnetic field, the charge, spin and electron correlation functions decay as powers of the critical exponents given by Eqns. (68) to (72), Eqns. (80) to (85) and Eqns. (91) to (94), respectively. The values of the critical exponents for small magnetic field, increase with increasing particle density nc, and magnetic field B, while increasing the interaction strength u, decreases the value of the critical exponents. Therefore, it is expected that our calculation will provide very useful insights in investigating how power-law behaviour affects other physical properties of interest in TL liquids. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML