-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2014; 4(6): 240-247
doi:10.5923/j.ijtmp.20140406.02
Bianchi Type-IX Bulk Viscous String Cosmological Model in f(R,T) Gravity with Special Form of Deceleration Parameter
H. R. Ghate, Atish S. Sontakke
Department of Mathematics, Jijamata Mahavidyalaya, Buldana, India
Correspondence to: H. R. Ghate, Department of Mathematics, Jijamata Mahavidyalaya, Buldana, India.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
A Bianchi type-IX bulk viscous string cosmological model has been investigated in the frame work of f(R,T) gravity proposed by Harko et al. (Phys. Rev. D 84:024020, 2011). The source for energy momentum tensor is bulk viscous fluid containing one dimensional cosmic strings. The field equations have been solved by applying a special form of deceleration parameter proposed by Singha and Debnath (IJTP 48:351, 2009). A barotropic equation of state for the pressure and energy density is assumed to get a determinate solution of the field equations. Also the bulk viscous pressure is assumed to be proportional to energy density. The physical and geometrical properties of the models are also discussed.
Keywords: f(R,T) Gravity, Cosmic Strings, Bulk Viscosity, Bianchi type-IX, Special form of Deceleration Parameter
Cite this paper: H. R. Ghate, Atish S. Sontakke, Bianchi Type-IX Bulk Viscous String Cosmological Model in f(R,T) Gravity with Special Form of Deceleration Parameter, International Journal of Theoretical and Mathematical Physics, Vol. 4 No. 6, 2014, pp. 240-247. doi: 10.5923/j.ijtmp.20140406.02.
Article Outline
1. Introduction
- It is well known that Einstein’s general theory of relativity has been successful in developing various cosmological models to study a structure formation and early stages of evolution of the universe. Einstein pointed out that general relativity does not account satisfactorily for inertial properties of matter i.e. Mach’s principle is not substantiated by general relativity. Several attempts have been made to generalize the general theory of gravitation by incorporating Mach’s principle and other desired features which were lacking in the original theory. Alternative theories of gravitation have been proposed to Einstein’s theory to incorporate certain desirable features in the general theory. In the last decades, as an alternative to general relativity, scalar tensor theories and modified theories of gravitation have been proposed. Brans and Dicke [1], Saez and Ballester [2] have much importance amongst the scalar-tensor theories of gravitation. Recently
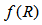 gravity and
gravity and 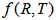 gravity [3, 4] theories have much importance amongst the modified theories of gravity because these theories are supposed to provide natural gravitation alternatives to dark energy. From the cosmological observations, it is known that the energy composition of the universe has 76% dark energy, 20% dark matter and 4% Baryon matter. This is confirmed by the high red shift supernovae experiments [5, 6] and cosmic microwave background radiation observations [7, 8]. Coperland et al. [9] have given a comprehensive review of
gravity [3, 4] theories have much importance amongst the modified theories of gravity because these theories are supposed to provide natural gravitation alternatives to dark energy. From the cosmological observations, it is known that the energy composition of the universe has 76% dark energy, 20% dark matter and 4% Baryon matter. This is confirmed by the high red shift supernovae experiments [5, 6] and cosmic microwave background radiation observations [7, 8]. Coperland et al. [9] have given a comprehensive review of 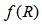 gravity and Harko et al. [4] proposed
gravity and Harko et al. [4] proposed 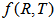 theory of gravity as an alternative amongst the modified theory of gravity of Einstein’s theory of gravitation. Several authors have studied
theory of gravity as an alternative amongst the modified theory of gravity of Einstein’s theory of gravitation. Several authors have studied 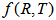 theory of gravity in different contexts [10-15]. Recently Chirde and Kadam [16] have studied A new class of Bianchi type bulk viscous and string cosmological model in
theory of gravity in different contexts [10-15]. Recently Chirde and Kadam [16] have studied A new class of Bianchi type bulk viscous and string cosmological model in 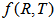 theory of gravitation. In
theory of gravitation. In 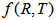 theory of gravity, the field equations are obtained from the Hilbert-Einstein type variation principle.
theory of gravity, the field equations are obtained from the Hilbert-Einstein type variation principle.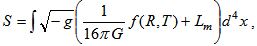 | (1) |
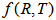 is an arbitrary function of the Ricci scalar R and the trace T of the stress-energy tensor of the matter
is an arbitrary function of the Ricci scalar R and the trace T of the stress-energy tensor of the matter 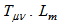 is the matter Lagrangian density.The stress-energy tensor of matter is defined as [17]
is the matter Lagrangian density.The stress-energy tensor of matter is defined as [17]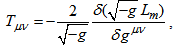 | (2) |
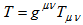 respectively. By assuming that the Lagrangian density
respectively. By assuming that the Lagrangian density 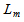 of matter depends only on the metric tensor components
of matter depends only on the metric tensor components 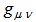 and not on its derivatives, we obtain
and not on its derivatives, we obtain 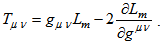 In the present paper, we use the natural system of units with
In the present paper, we use the natural system of units with 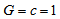 so that the Einstein gravitational constant is defined as
so that the Einstein gravitational constant is defined as 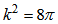 .The corresponding field equations of the
.The corresponding field equations of the 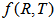 gravity are found by varying the action with respect to the metric
gravity are found by varying the action with respect to the metric 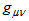 [4]:
[4]: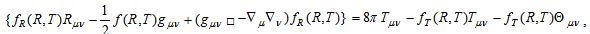 | (3) |
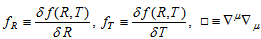 ,
,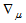 is the covariant derivative and
is the covariant derivative and 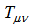 is the standard matter energy-momentum tensor derived from the Lagrangian
is the standard matter energy-momentum tensor derived from the Lagrangian 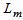 .Contracting (3) gives the relation between the Ricci scalar
.Contracting (3) gives the relation between the Ricci scalar 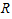 and the trace
and the trace 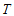 of the stress-energy tensor,
of the stress-energy tensor,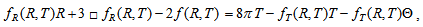 | (4) |
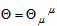 .Generally the field equations also depend [through the tensor
.Generally the field equations also depend [through the tensor 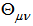 ] on the physical nature of the matter field. Hence several theoretical models corresponding to different matter sources in
] on the physical nature of the matter field. Hence several theoretical models corresponding to different matter sources in 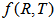 gravity can be obtained.By considering some particular class of
gravity can be obtained.By considering some particular class of 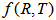 modified gravity model obtained by explicitly specifying the functional form of
modified gravity model obtained by explicitly specifying the functional form of 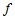 . Assuming that the function
. Assuming that the function 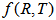 given by
given by 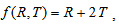 | (5) |
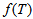 is an arbitrary function of the trace of the stress-energy tensor of matter.From equation (3), the gravitational field equations are given by
is an arbitrary function of the trace of the stress-energy tensor of matter.From equation (3), the gravitational field equations are given by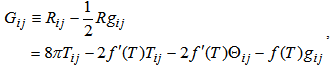 | (6) |
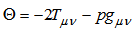 then the above equation (6) reduces to
then the above equation (6) reduces to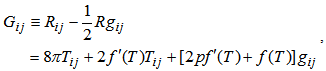 | (7) |
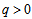 , (ii) an expansion with constant rate if
, (ii) an expansion with constant rate if 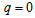 , (iii) accelerating power law expansion if
, (iii) accelerating power law expansion if 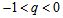 , (iv) exponential expansion (de-Sitter expansion) if
, (iv) exponential expansion (de-Sitter expansion) if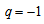 (v) super-exponential expansion if
(v) super-exponential expansion if 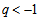 . Many relativists have studied DE cosmological models with different form of deceleration parameters. Singha and Debnath [18], Adhav et al. [19, 20] have obtained DE models with special form of deceleration parameter. The study of Bianchi type cosmological models are important in achieving better understanding of anisotropy in the universe. Moreover the anisotropic universes have greater generality than FRW isotropic models. The simplicity of the field equations made Bianchi type space-times useful. Bianchi type I-IX cosmological models are homogeneous and anisotropic. Bianchi type-IX universe are studied by the number of cosmologists because of familiar solutions like Robertson–Walker Universe, the de-sitter universe, the Taub-Nut solutions etc. Chakraborty [21], Bali and Dave [22], Bali and Yadav [23], Pradhan et al. [24], Tyagi et al. [25], Ghate and Sontakke [26, 27] have obtained Bianchi type-IX cosmological models in different contexts. Bulk viscosity plays a very important role in getting accelerated expansion of the universe. The matter behaves like viscous fluid in the early stages of the universe when neutrinos decoupling occurs. The effect of viscosity on the evolution of the universe had been studied by Misner [28, 29]. Several authors have studied bulk viscous cosmological models in general relativity [30-37] Johri and Sudharsan [38], Pimental [39], Banerjee and Beesham [40], Singh et al. [41], Rao et al. [42], Naidu et al. [43], Reddy et al. [44] have studied bulk viscous string cosmological models in scalar-tensor theories of gravitation. Recently Naidu et al. [45], Reddy et al. [46] have studied Bianchi type-V and Kaluza-Klein cosmological models with bulk viscosity and cosmic strings in
. Many relativists have studied DE cosmological models with different form of deceleration parameters. Singha and Debnath [18], Adhav et al. [19, 20] have obtained DE models with special form of deceleration parameter. The study of Bianchi type cosmological models are important in achieving better understanding of anisotropy in the universe. Moreover the anisotropic universes have greater generality than FRW isotropic models. The simplicity of the field equations made Bianchi type space-times useful. Bianchi type I-IX cosmological models are homogeneous and anisotropic. Bianchi type-IX universe are studied by the number of cosmologists because of familiar solutions like Robertson–Walker Universe, the de-sitter universe, the Taub-Nut solutions etc. Chakraborty [21], Bali and Dave [22], Bali and Yadav [23], Pradhan et al. [24], Tyagi et al. [25], Ghate and Sontakke [26, 27] have obtained Bianchi type-IX cosmological models in different contexts. Bulk viscosity plays a very important role in getting accelerated expansion of the universe. The matter behaves like viscous fluid in the early stages of the universe when neutrinos decoupling occurs. The effect of viscosity on the evolution of the universe had been studied by Misner [28, 29]. Several authors have studied bulk viscous cosmological models in general relativity [30-37] Johri and Sudharsan [38], Pimental [39], Banerjee and Beesham [40], Singh et al. [41], Rao et al. [42], Naidu et al. [43], Reddy et al. [44] have studied bulk viscous string cosmological models in scalar-tensor theories of gravitation. Recently Naidu et al. [45], Reddy et al. [46] have studied Bianchi type-V and Kaluza-Klein cosmological models with bulk viscosity and cosmic strings in 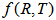 theory of gravitation. Motivated by the above discussion and investigations in
theory of gravitation. Motivated by the above discussion and investigations in 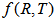 modified theory of gravity, in this paper we have investigated Bianchi type-IX bulk viscous string cosmological model in
modified theory of gravity, in this paper we have investigated Bianchi type-IX bulk viscous string cosmological model in 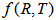 theory of gravity with special form of deceleration parameter. Bianchi type-IX space-time has considered when universe is filled with cosmic strings and bulk viscosity in
theory of gravity with special form of deceleration parameter. Bianchi type-IX space-time has considered when universe is filled with cosmic strings and bulk viscosity in 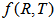 theory of gravity with special form of deceleration parameter. This work is organized as follows: In Section 2, the model and field equations have been presented. The field equations have been solved in Section 3 by applying special form of deceleration parameter. The physical and geometrical behavior of the model have been discussed in Section 4. In the last Section 5, concluding remarks have been expressed.
theory of gravity with special form of deceleration parameter. This work is organized as follows: In Section 2, the model and field equations have been presented. The field equations have been solved in Section 3 by applying special form of deceleration parameter. The physical and geometrical behavior of the model have been discussed in Section 4. In the last Section 5, concluding remarks have been expressed.2. Metric and Field Equations
- Bianchi type-IX metric is considered in the form,
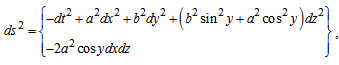 | (8) |
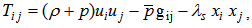 | (9) |
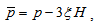 | (10) |
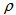 is the rest energy density of the system,
is the rest energy density of the system, 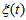 is the coefficient of bulk viscosity,
is the coefficient of bulk viscosity, 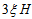 is bulk viscous pressure, H is Hubble’s parameter,
is bulk viscous pressure, H is Hubble’s parameter, 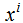 is the direction of the string and
is the direction of the string and 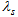 is the string tension density. Also
is the string tension density. Also 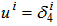 is a four-velocity vector which satisfies
is a four-velocity vector which satisfies 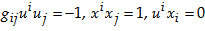 . Here we consider
. Here we consider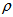 ,
, 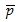 and
and 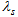 as function of time t only.We assume the string to be lying along the x-axis. One-dimensional strings are assumed to be loaded with particles and the particle energy density is
as function of time t only.We assume the string to be lying along the x-axis. One-dimensional strings are assumed to be loaded with particles and the particle energy density is 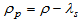 .In co-moving coordinate system, we get
.In co-moving coordinate system, we get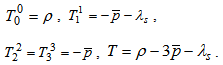 | (11) |
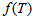 of the trace of the stress-energy tensor of the matter so that
of the trace of the stress-energy tensor of the matter so that 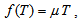 | (12) |
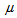 is constant.In the co-moving coordinate system, the field equations (7) for the metric (8) and with the help of (9)-(12) can be written as
is constant.In the co-moving coordinate system, the field equations (7) for the metric (8) and with the help of (9)-(12) can be written as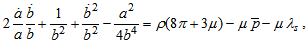 | (13) |
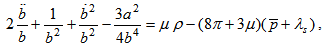 | (14) |
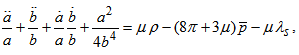 | (15) |
 denotes the differentiation with respect to t.
denotes the differentiation with respect to t. 3. Solutions of Field Equations
- The field equations (13)–(15) are a system three independent equations in six unknowns
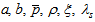 . Three additional conditions relating these unknowns may be used to obtain explicit solutions of the systems.(i) Firstly, we assume that the expansion
. Three additional conditions relating these unknowns may be used to obtain explicit solutions of the systems.(i) Firstly, we assume that the expansion 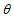 in the model is proportional to the shear
in the model is proportional to the shear 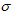 . This condition leads to
. This condition leads to 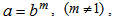 | (16) |
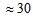 percent [48, 49]. Collin et al. [50] have pointed out that for spatially homogeneous metric, the normal congruence to the homogeneous expansion satisfies that the condition
percent [48, 49]. Collin et al. [50] have pointed out that for spatially homogeneous metric, the normal congruence to the homogeneous expansion satisfies that the condition 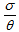 is constant.(ii) Secondly for a barotropic fluid, the combined effect of the proper pressure and the bulk viscous pressure can be expressed as
is constant.(ii) Secondly for a barotropic fluid, the combined effect of the proper pressure and the bulk viscous pressure can be expressed as 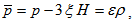 | (17) |
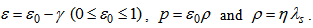 Here
Here 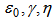 are constants.(iii) Lastly following Singha and Debnath [17], we use a special form of deceleration parameter as:
are constants.(iii) Lastly following Singha and Debnath [17], we use a special form of deceleration parameter as: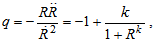 | (18) |
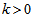 is constant.Solving equation (18), the average scale factor R is given by
is constant.Solving equation (18), the average scale factor R is given by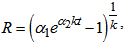 | (19) |
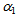 and
and 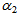 are constants of integration. For the metric (8), the scale factor R is given by
are constants of integration. For the metric (8), the scale factor R is given by 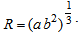 | (20) |
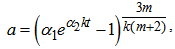 | (21) |
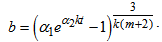 | (22) |
 | (23) |
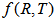 gravity with special form of deceleration parameter.
gravity with special form of deceleration parameter.4. Some Physical Properties of the Model
- For the cosmological model (23), the physical quantities Spatial volume
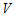 , Hubble parameter
, Hubble parameter 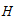 , Expansion scalar
, Expansion scalar 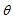 , Mean Anisotropy parameter
, Mean Anisotropy parameter 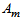 , Shear scalar
, Shear scalar 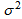 , Energy density
, Energy density 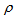 , String tension density
, String tension density 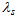 , Bulk viscosity pressure
, Bulk viscosity pressure 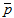 , Coefficient of bulk viscosity
, Coefficient of bulk viscosity 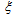 and Particle energy density
and Particle energy density 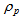 are obtained as follows :Spatial volume,
are obtained as follows :Spatial volume,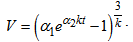 | (24) |
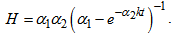 | (25) |
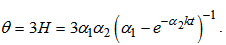 | (26) |
 | (27) |
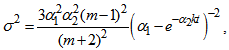 | (28) |
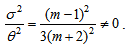 | (29) |
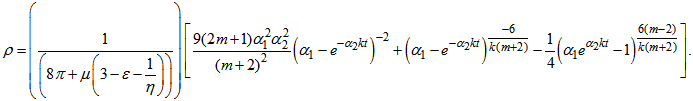 | (30) |
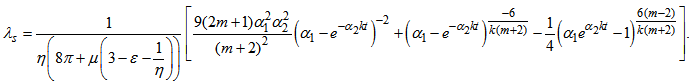 | (31) |
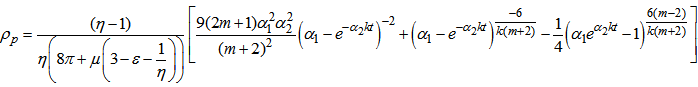 | (32) |
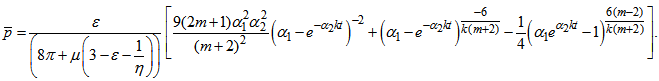 | (33) |
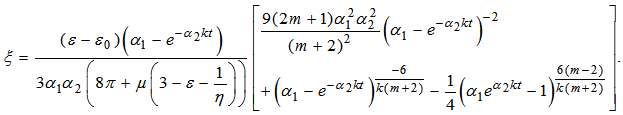 | (34) |
4.1. Physical Behavior of the Model
- For the cosmological model (23), we observed that, the spatial scale factors has finite value at the initial epoch
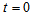 and increases for large values of t. In particular for
and increases for large values of t. In particular for 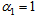 and
and 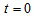 , the model has a big bang type singularity. It can also be observed that, at
, the model has a big bang type singularity. It can also be observed that, at 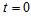 , the universe starts evolving with finite volume and expands infinitely with the increase in cosmic time t (Figure 1). The values of expansion
, the universe starts evolving with finite volume and expands infinitely with the increase in cosmic time t (Figure 1). The values of expansion 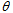 and shear
and shear 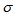 tend to infinity for large values of
tend to infinity for large values of 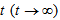 showing that the universe is expanding with increase of time (Figure 3, 4).From equations (27) and (29), the mean anisotropy parameter
showing that the universe is expanding with increase of time (Figure 3, 4).From equations (27) and (29), the mean anisotropy parameter 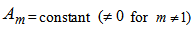 and
and 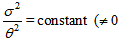
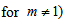 indicates that the model is anisotropic throughout the evolution of the universe except at
indicates that the model is anisotropic throughout the evolution of the universe except at 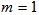 (i.e. the model does not approach isotropy). In figure 5, the plot of deceleration parameter verses time is given from which we conclude that the model is decelerating at an initial phase and changes the expansion from decelerating to accelerating. Hence the model is consistent with the recent cosmological observations [5-6, 51-55].Bulk viscosity in the model decreases with increase in time which is in accordance with the well-known fact that bulk viscosity decreases with time and leads to inflationary model [56].For illustrative purposes, evolutionary behaviors of some cosmological parameters are shown graphically (Figure 1-5).
(i.e. the model does not approach isotropy). In figure 5, the plot of deceleration parameter verses time is given from which we conclude that the model is decelerating at an initial phase and changes the expansion from decelerating to accelerating. Hence the model is consistent with the recent cosmological observations [5-6, 51-55].Bulk viscosity in the model decreases with increase in time which is in accordance with the well-known fact that bulk viscosity decreases with time and leads to inflationary model [56].For illustrative purposes, evolutionary behaviors of some cosmological parameters are shown graphically (Figure 1-5).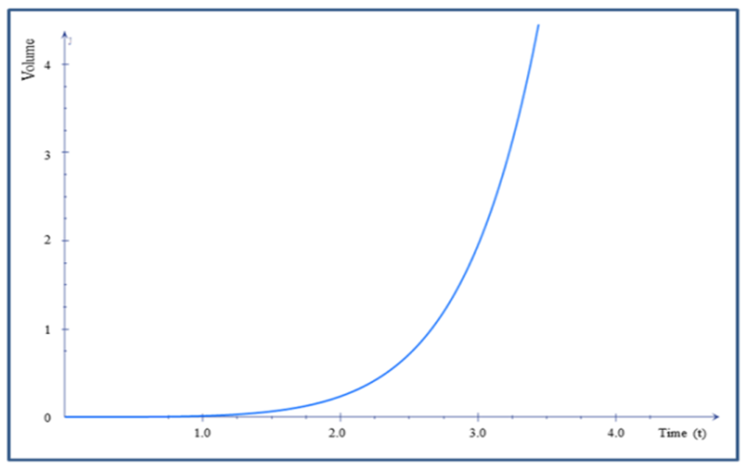 | Figure 1. The Plot of Volume verses time |
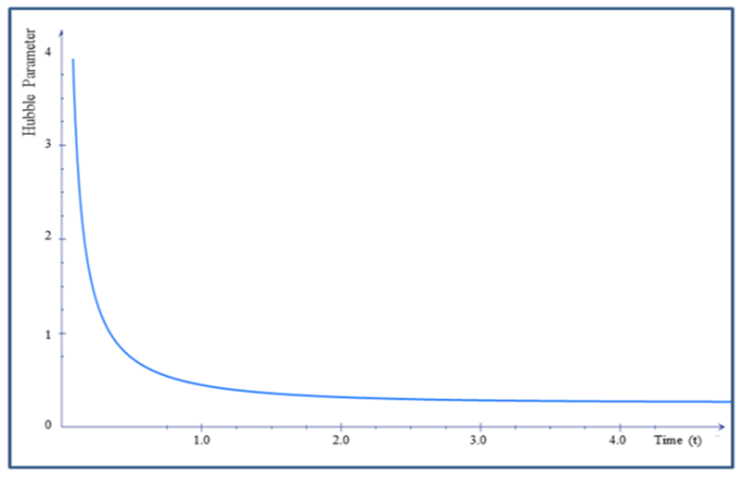 | Figure 2. The Plot of Hubble parameter verses time |
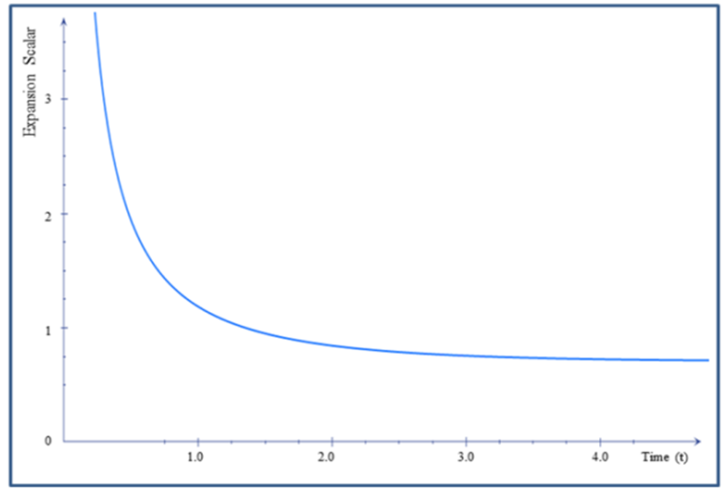 | Figure 3. The Plot of Expansion scalar verses time |
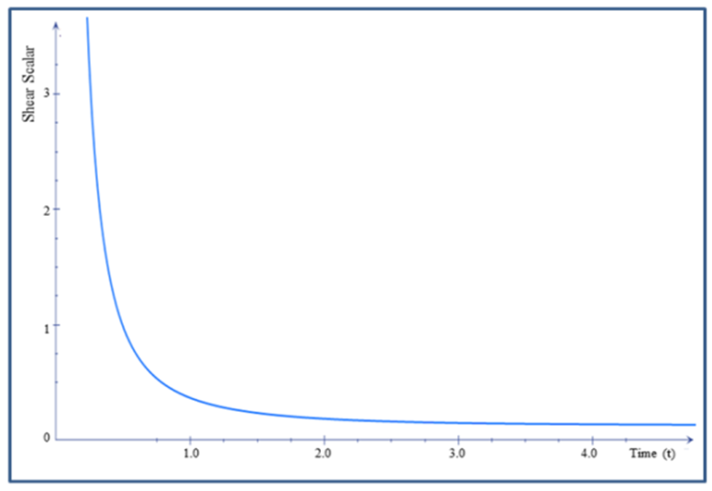 | Figure 4. The Plot of Shear scalar verses time |
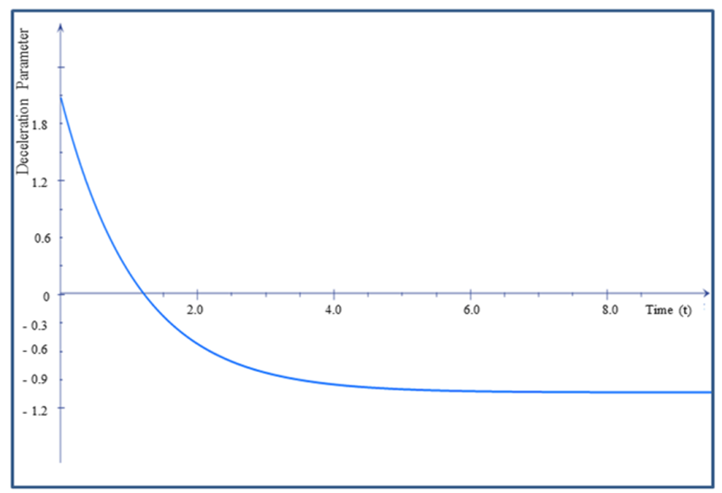 | Figure 5. The Plot of deceleration parameter verses time |
5. Conclusions
- Bianchi type-IX bulk viscous strings cosmological model has been discussed in the frame work of gravity proposed by Harko et al. (Phys. Rev. D 84:024020, 2011) when the source for energy momentum tensor is bulk viscous fluid containing one dimensional cosmic strings. The solution of the field equations has obtained by choosing the special form of deceleration parameter
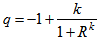 . It is observed that in early phase of universe, the value of deceleration parameter is positive while as
. It is observed that in early phase of universe, the value of deceleration parameter is positive while as 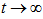 , the value of
, the value of 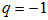 . Hence the universe had a decelerated expansion in the past and has accelerated expansion at present which is in good agreement with the recent observations of SN Ia. It is worth to mention that, the model obtained is point type singular, expanding, shearing, non-rotating and do not approach isotropy for large t. Further the models are anisotropic throughout the evolution. This shows that the present model not only represent accelerating universe but also confirms the well-known fact that the bulk viscosity will play a vital role in getting the accelerated expansion. We hope that our model will be useful in the discussion of structure formation in the early universe and an accelerating expansion of the universe at present.
. Hence the universe had a decelerated expansion in the past and has accelerated expansion at present which is in good agreement with the recent observations of SN Ia. It is worth to mention that, the model obtained is point type singular, expanding, shearing, non-rotating and do not approach isotropy for large t. Further the models are anisotropic throughout the evolution. This shows that the present model not only represent accelerating universe but also confirms the well-known fact that the bulk viscosity will play a vital role in getting the accelerated expansion. We hope that our model will be useful in the discussion of structure formation in the early universe and an accelerating expansion of the universe at present. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML