-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2014; 4(6): 225-239
doi:10.5923/j.ijtmp.20140406.01
Ring of Large Number Mutually Coupled Oscillators – Periodic Solutions
Vasil G. Angelov1, Dafinka Tz. Angelova2
1Department Name of Mathematics, University of Mining and Geology “St. I. Rilski”, Sofia, Bulgaria
2Department of Mechanics and Mathematics, University of Structural Engineering & Architecture (VSU) “L. Karavelov”, Sofia, Bulgaria
Correspondence to: Vasil G. Angelov, Department Name of Mathematics, University of Mining and Geology “St. I. Rilski”, Sofia, Bulgaria.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
The paper is devoted to the investigation of periodic regimes of a ring of a large number mutually coupled oscillators with active elements characterized by a simple symmetric cubic nonlinearity. In contrast to the usually accepted approach leading to Van der Pol equations we reduce the original system describing the ring oscillator to a first order integro-differential one. Introducing a suitable function space we define an operator acting in this space and by fixed point method we prove the basic result: an existence-uniqueness of T0-periodic solution of the obtained integro-differential system. Finally we give a numerical example.
Keywords: Oscillators, Coupled oscillators, Ring of oscillators, Van der Pol differential equations, Integro-differential system, Periodic solutions, Fixed-point theorem
Cite this paper: Vasil G. Angelov, Dafinka Tz. Angelova, Ring of Large Number Mutually Coupled Oscillators – Periodic Solutions, International Journal of Theoretical and Mathematical Physics, Vol. 4 No. 6, 2014, pp. 225-239. doi: 10.5923/j.ijtmp.20140406.01.
Article Outline
1. Introduction
- Oscillatory behavior is ubiquitous in all physical systems in different disciplines ranging from biology and chemistry to engineering and physics, especially in electronic and optical systems. In radio frequency and lightwave communication systems, oscillators are used for transformation signals and channel selection. Oscillators are also present in all digital electronic systems, which require a time reference. Coupled oscillators are oscillators connected in such a way that energy can be transferred between them. Since about 1960, mathematical biologists have been studying simplified models of coupled oscillators that retain the essence of their biological prototypes: pacemaker cells in the heart, insulin-secreting cells in the pancreas; and neural networks in the brain and spinal cord that control such rhythmic behavior as breathing, running and chewing. Ring of coupled oscillators is cascaded combination of delay stages, connected in a close loop chain and it has a number of applications in communication systems, especially in anatomic – organs such as the heart, intestine and ureter consist of many cellular oscillators coupled together. An ideal oscillator would provide a perfect time reference, i.e., a periodic signal. However all physical oscillators are corrupted by undesired perturbation noise. Hence signals, generated by physical oscillators, are not perfectly periodic.Mathematical basis of coupled oscillators has been established in [1], [2] and mutual synchronization of a large number of oscillators has been investigated in [3]. Very interesting applications can be found in [4] and [5]. In [6] the authors have investigated a ring array of van der Pol oscillators and clarified each mode structure. Their results are based on the method of equivalent linearization of the nonlinear terms using Krylov-Bogoliubov method. An active element is characterized by a simple symmetric cubic nonlinearity, that is, with V-I characteristic
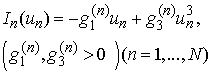 .A ring oscillator is described by the following integro-differential system:
.A ring oscillator is described by the following integro-differential system: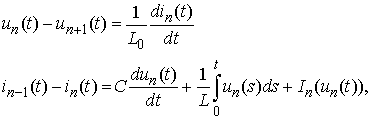 | (1) |
 The usually accepted approach (cf. [6]) is to exclude the current functions after differentiation and to obtain a second order system of van der Pol differential equations
The usually accepted approach (cf. [6]) is to exclude the current functions after differentiation and to obtain a second order system of van der Pol differential equations 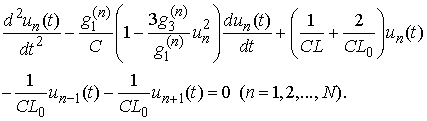 Here we consider the original integro-differential system (1) and exclude current functions without differentiation. So we reach the following first order (instead of second order) integro-differential system:
Here we consider the original integro-differential system (1) and exclude current functions without differentiation. So we reach the following first order (instead of second order) integro-differential system: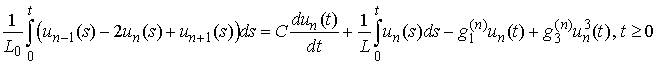
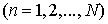 or
or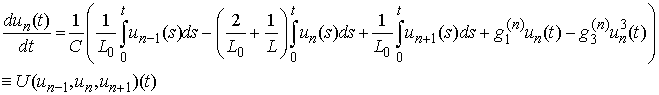
 .In view of the boundary conditions for the ring connection
.In view of the boundary conditions for the ring connection  .the above system yields the following system of N equations for N unknown functions.
.the above system yields the following system of N equations for N unknown functions.  | (2) |
 .We define an operator acting on suitable function space and its fixed point is a periodic solution of the above system. The advantages of our method is its simpler technique and obtaining of successive approximations beginning with simple initial functions.We formulate a periodic problem: to find a periodic solution
.We define an operator acting on suitable function space and its fixed point is a periodic solution of the above system. The advantages of our method is its simpler technique and obtaining of successive approximations beginning with simple initial functions.We formulate a periodic problem: to find a periodic solution 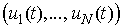 on
on 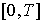 of the system (2). To solve the periodic problem we use the method from [7]. By
of the system (2). To solve the periodic problem we use the method from [7]. By 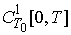 we mean the space of all differentiable
we mean the space of all differentiable 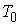 -periodic functions with continuous derivatives.First we introduce the sets (assuming
-periodic functions with continuous derivatives.First we introduce the sets (assuming 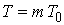 ):
):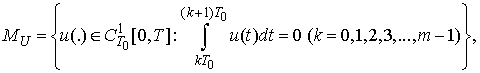
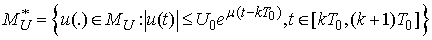
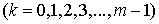 The set
The set 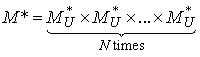 turns out into a complete metric space with respect to the metric:
turns out into a complete metric space with respect to the metric: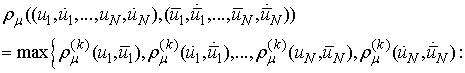
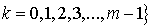 where
where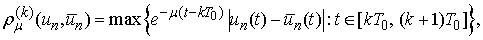
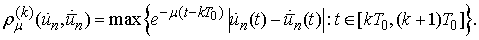 It is easy to see
It is easy to see 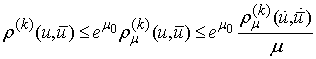 .Introduce the operator B as a n-tuple
.Introduce the operator B as a n-tuple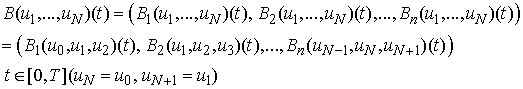 defined on every interval
defined on every interval 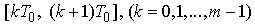 by the expressions
by the expressions 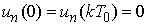 ;
;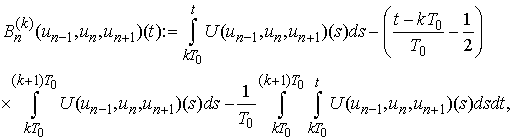
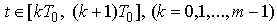 ,
, 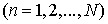 ,where
,where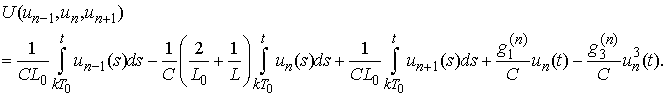
2. Preliminary Results
- Now we formulate some useful preliminary assertions for our investigation. Lemma 1. If
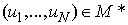 then
then 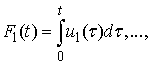
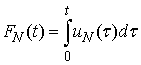 are
are 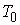 -periodic functions.Proof: Indeed, we have
-periodic functions.Proof: Indeed, we have 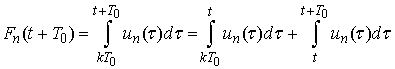
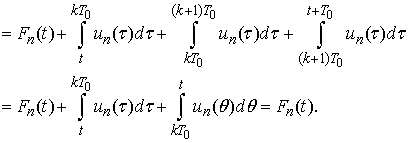 Lemma 1 is thus proved.Lemma 2. If
Lemma 1 is thus proved.Lemma 2. If 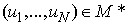 then
then 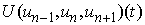 are
are 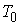 -periodic functions.The proof is straightforward based on the previous Lemma 1.Lemma 3. For every
-periodic functions.The proof is straightforward based on the previous Lemma 1.Lemma 3. For every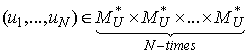 it follows
it follows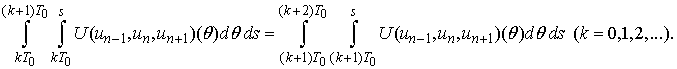 Proof:We notice that in view of Lemma 2 the functions
Proof:We notice that in view of Lemma 2 the functions 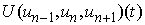 are
are 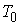 -periodic. Let us define the functions
-periodic. Let us define the functions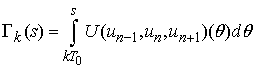 and
and 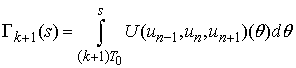 and rewrite them in the form
and rewrite them in the form 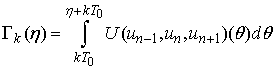 ,
,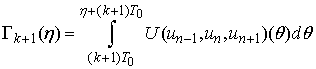 .Changing the variable
.Changing the variable 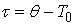 we obtain
we obtain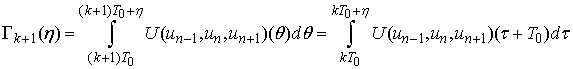
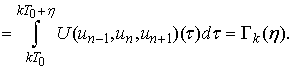 Consequently
Consequently 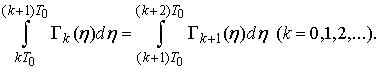 Lemma 3 is thus proved.Lemma 3 shows that operator function
Lemma 3 is thus proved.Lemma 3 shows that operator function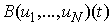 is
is 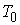 - periodic one.Lemma 4. The initial value problem (2) has a solution
- periodic one.Lemma 4. The initial value problem (2) has a solution 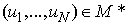 iff the operator B has a fixed point
iff the operator B has a fixed point 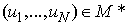 , that is,
, that is, 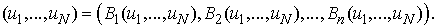 Proof: Let
Proof: Let 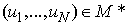 be a periodic solution of (2). Then integrating (2) we have:
be a periodic solution of (2). Then integrating (2) we have: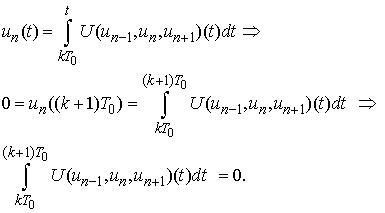 But
But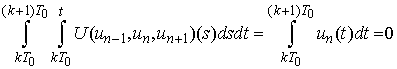 .Therefore
.Therefore 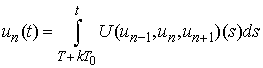 is equivalent to
is equivalent to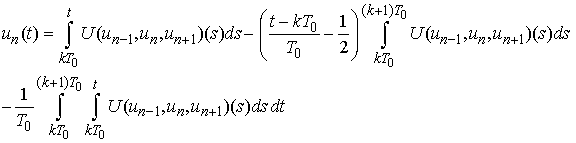 and then the solution
and then the solution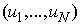 of (2) is a fixed point of B. Conversely, let
of (2) is a fixed point of B. Conversely, let 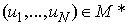 be a fixed point B, that is,
be a fixed point B, that is, 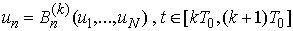 .Therefore by definition of B we obtain
.Therefore by definition of B we obtain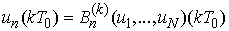 ,or
,or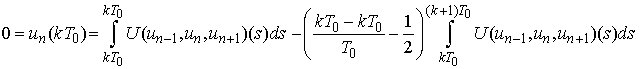
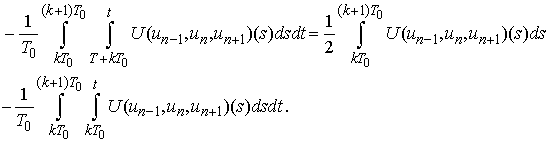 We show
We show 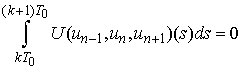 which implies
which implies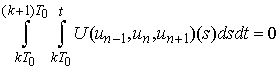 .Indeed, put
.Indeed, put 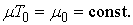 and then we have
and then we have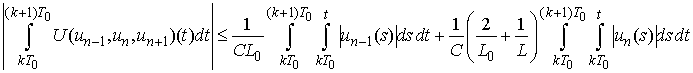
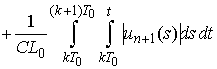
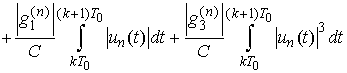
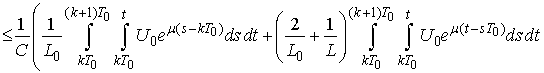
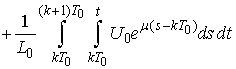
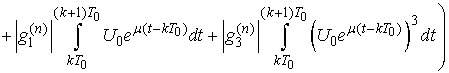
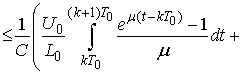
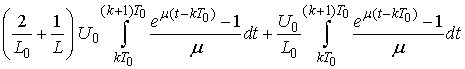
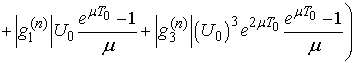
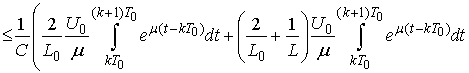

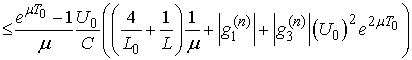
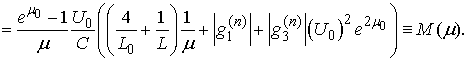 Obviously
Obviously 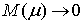 as
as 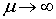 that implies
that implies 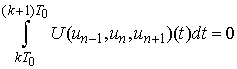 .Therefore the operator equation
.Therefore the operator equation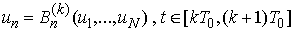 becomes
becomes 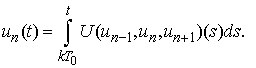 Differentiating the last equalities we obtain (2).Lemma 4 is thus proved.
Differentiating the last equalities we obtain (2).Lemma 4 is thus proved. 3. Main Result
- Theorem 1. Let the following assumptions be valid:1)
 ;2) For sufficiently large
;2) For sufficiently large 
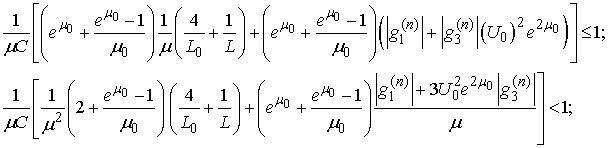
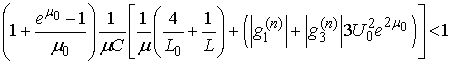 .Then there exists a unique
.Then there exists a unique 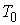 -periodic solution of (2).Proof: First we show that
-periodic solution of (2).Proof: First we show that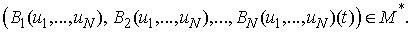 Indeed
Indeed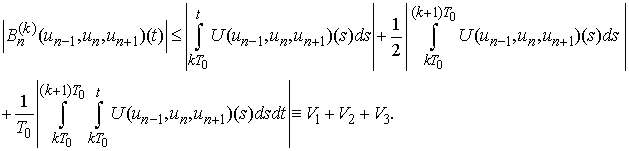 We have
We have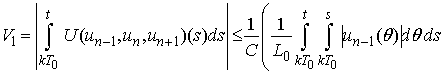
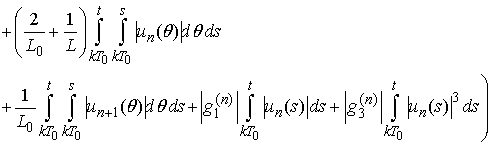
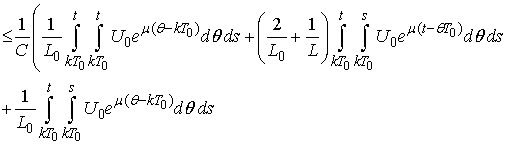
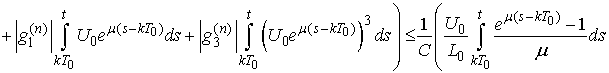
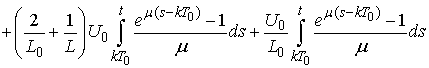
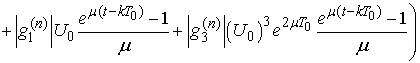
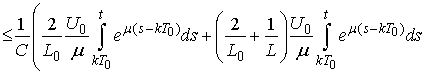
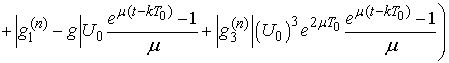
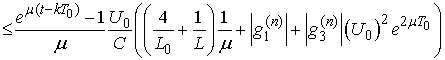
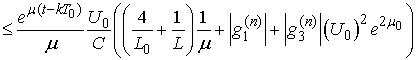 .Using the estimates from Lemma 3 we obtain
.Using the estimates from Lemma 3 we obtain 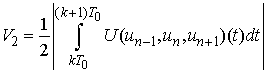
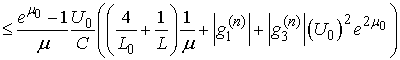 and
and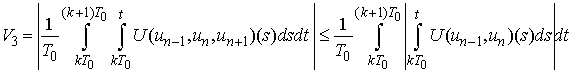
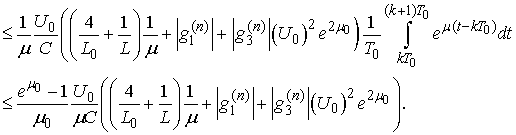 Therefore for sufficiently large
Therefore for sufficiently large 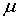 we have
we have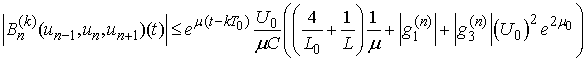
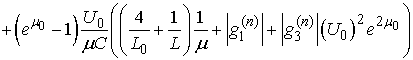
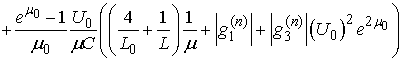
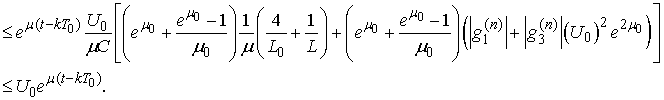 It remains to show that
It remains to show that 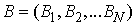 is a contractive operator on
is a contractive operator on 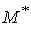 .Indeed,
.Indeed,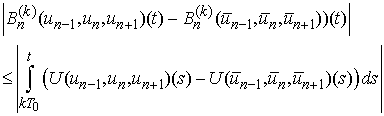
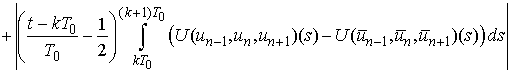
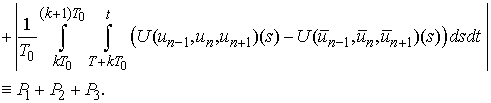 Then
Then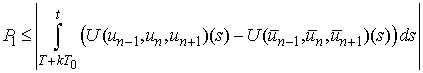
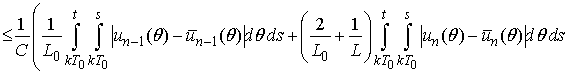
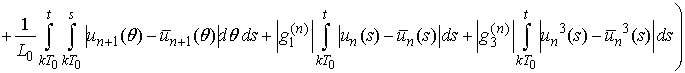
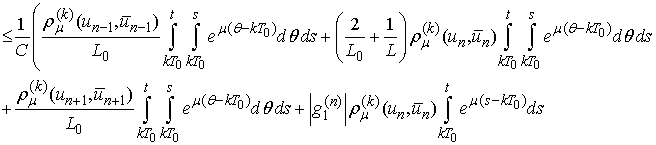
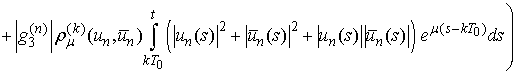
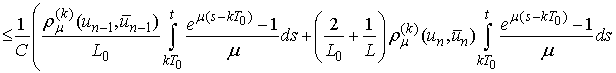
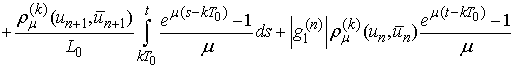
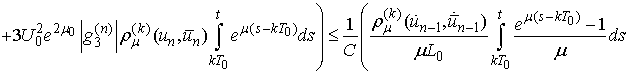
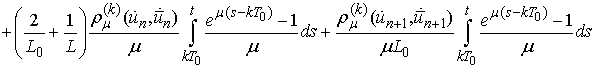
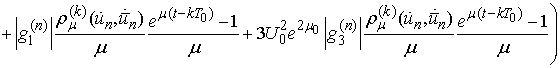
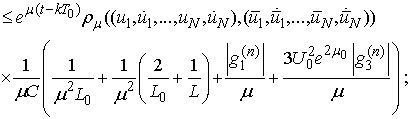
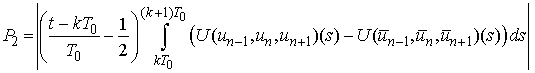
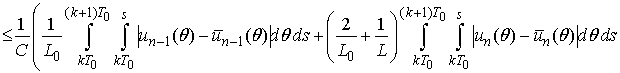
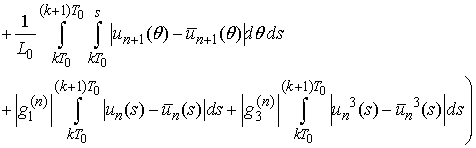
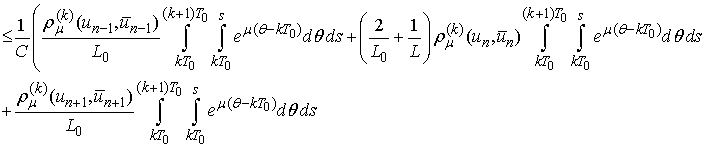
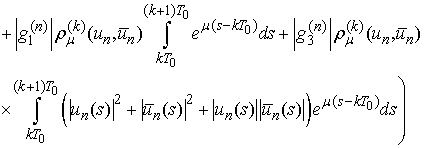
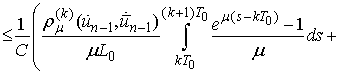
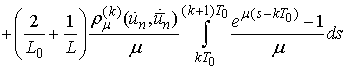
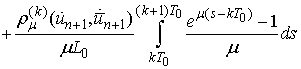
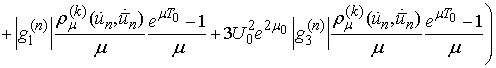
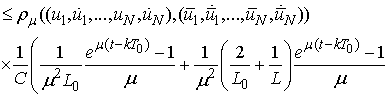
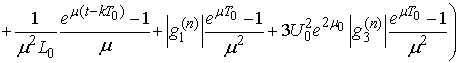
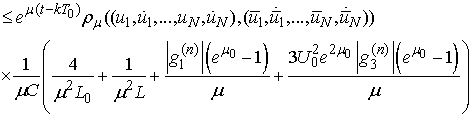 and
and 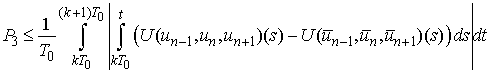
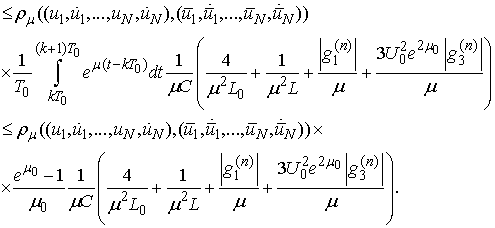 It follows
It follows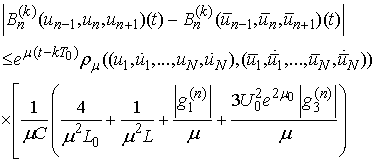
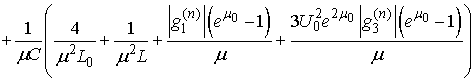
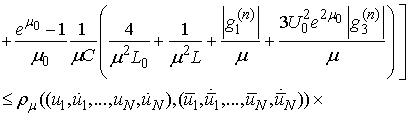
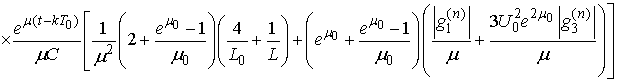
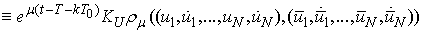 .Thus
.Thus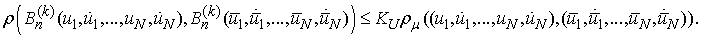 For the derivative we obtain
For the derivative we obtain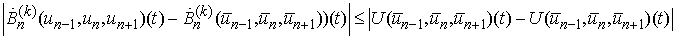
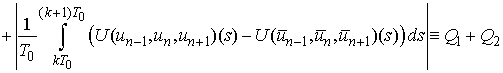 .We have
.We have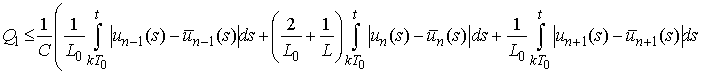
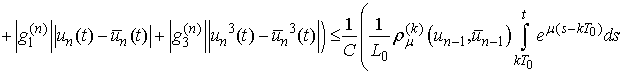
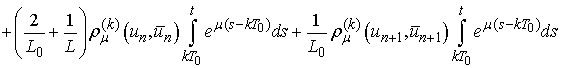
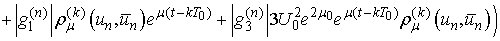
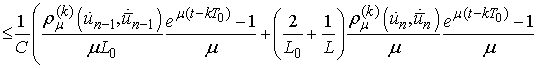
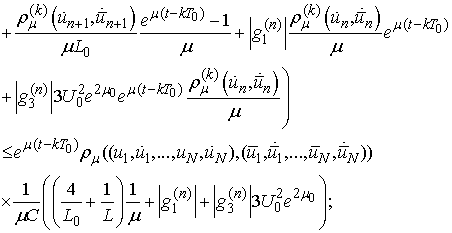
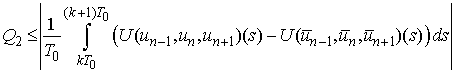
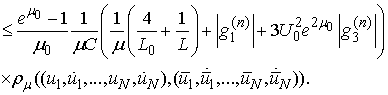 Thus
Thus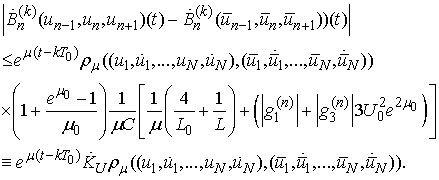 The above inequalities imply
The above inequalities imply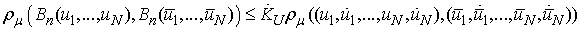 and then
and then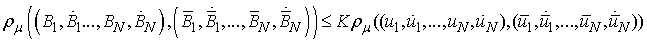 where
where 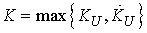 .Theorem 1 is thus proved.
.Theorem 1 is thus proved. 4. Numerical Example
- The inequalities guaranteeing an existence-uniqueness of a periodic solution are
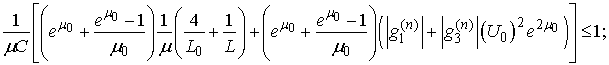
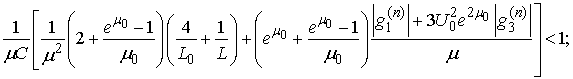
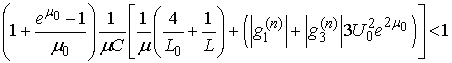 .Let us consider the case when
.Let us consider the case when 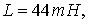
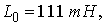
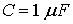 . We assume the active elements have characteristics
. We assume the active elements have characteristics 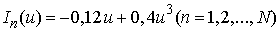 . Then
. Then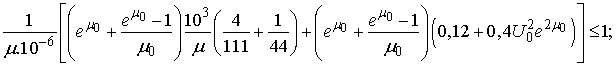 ;
;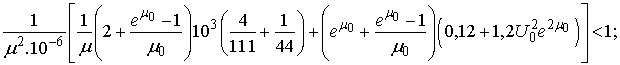
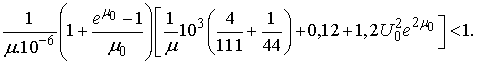 If for instance
If for instance 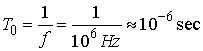 , and
, and 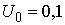 . Then we have to choose
. Then we have to choose 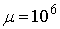 and the second inequality can be disregarded. Then
and the second inequality can be disregarded. Then 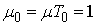 that implies
that implies 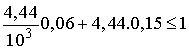 and hence
and hence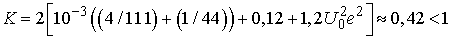 .
.5. Conclusions
- Successive approximations to the solution can be obtained beginning with the following initial functions
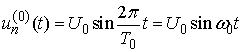 . It is easy to calculate the next approximation from the right-hand side of the above system:
. It is easy to calculate the next approximation from the right-hand side of the above system: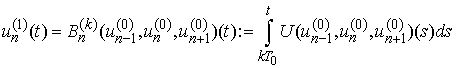
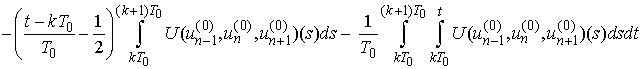
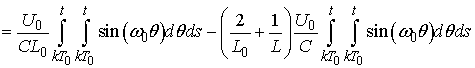
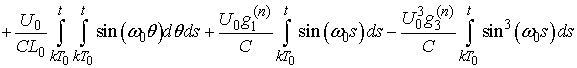
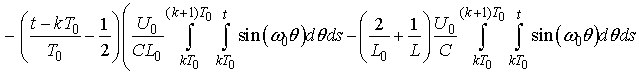
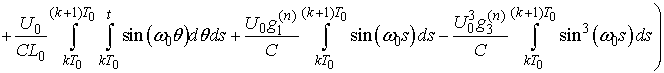
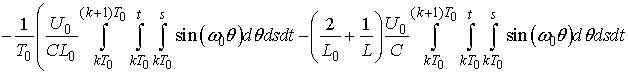
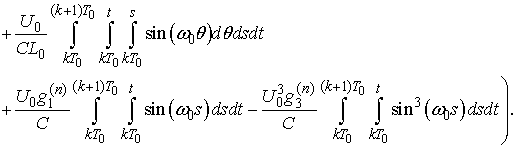 Principal Remark. Once we have found the voltages in view of (1) we solve the equations with respect to
Principal Remark. Once we have found the voltages in view of (1) we solve the equations with respect to 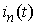 :
: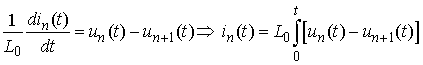 ,where
,where 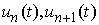 are already known functions.The currents are periodic functions too:
are already known functions.The currents are periodic functions too: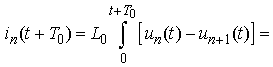
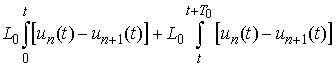
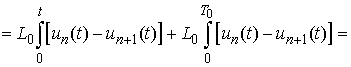
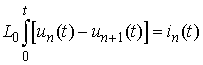 .
. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML