1. Introduction

The general theory of relativity has been called by Misner, Thorne and Wheeler [1] as Geometrodynamics. The curvature of space and time together as a four dimensional entity causes straight lines or geodesics to appear as some sort of a result of interaction between masses. Also the nonlinear nature of the ‘field’ equations causes a body moving under the attractive force of another usually much more massive body to ‘deviate from geodesics’ due to its own mass. This is usually a small effect and here we shall neglect it. We intend to study two effects due to this geometrodynamical nature of gravity which causes it to strongly deviate from the common sense conception of gravity when the field itself is very strong. Some of these effects especially that described in section 3 is physically testable and is essentially a continuation of my previous work [2].

2. The First Effect

It is well known that bodies whose radius is below r=2m (m is the mass of the body and the units are such that G=1 and c=1) the laws of physics for r<2m behave very differently from those in normal space-time. However we will show one instance when there is no black hole present a hypothetical negative density of matter can give rise to a pressure gradient which is very different from what Newtonian gravity predicts. For example consider a density of spherically symmetric distribution of stellar matter given by [3]

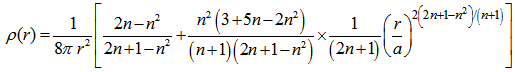One can show that for n=2.1 when the mass m and radius a of the body satisfy

,

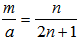this distribution of matter cannot create a black hole. The pressure as a function of the radial coordinate as given in reference [3] is

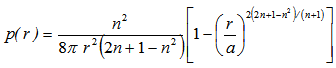The plots of ρ and dp/dr as a function of r is shown in figures 1 and 2 respectively for a body with mass equal to the solar mass m=1.475 km (that is a=3.652 km). We find that ρ is negative for some values of r (the radial coordinate) and positive for others but the pressure gradient is always negative. One can argue that negative density is nonexistent in the real world but still it can be treated as a mathematical object. Newtonian gravity predicts a rapidly changing pressure gradient (from –ve to +ve) at the interface of the negative and positive density regions unlike the function in fig. 2.

Figure 1. The density of stellar matter described in the text as a function of the radial coordinate r in km for a limited range of r

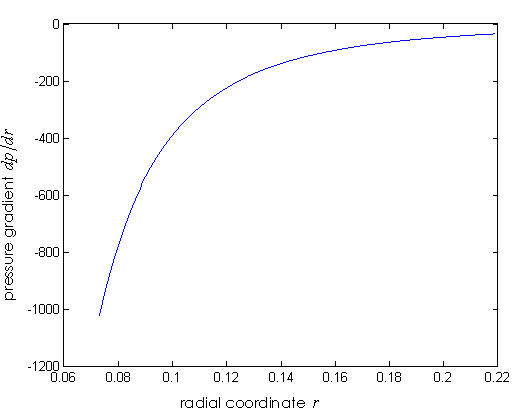Figure 2. The pressure gradient as a function of r in km for the matter distribution of fig. 1

3. The Second Effect

It has been shown in a previous formulation of mine [2] following the method of Darwin [4, 5] that geodesic equations of motion give rise to peculiar orbital shapes near black holes. Here we study ‘elliptical’ orbits and show that their apastrons violently precess if the particle periastron approaches a coordinate distance slightly greater than 2m from a Schwarzschild black hole horizon (that is a value of the radial coordinate about r=4m). The orbit we consider has a high eccentricity e=0.9. The equations relating the radial coordinate with the azimuthal angular coordinate as given on pages 40-41 of reference [5] are expressed as

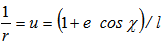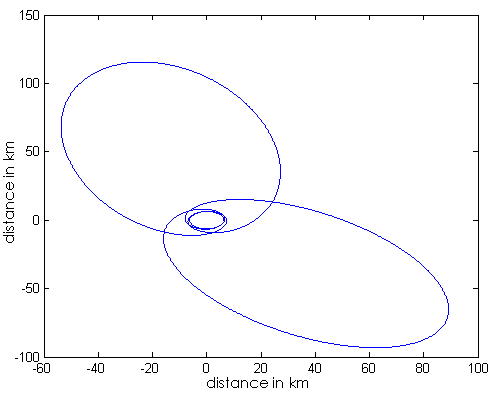
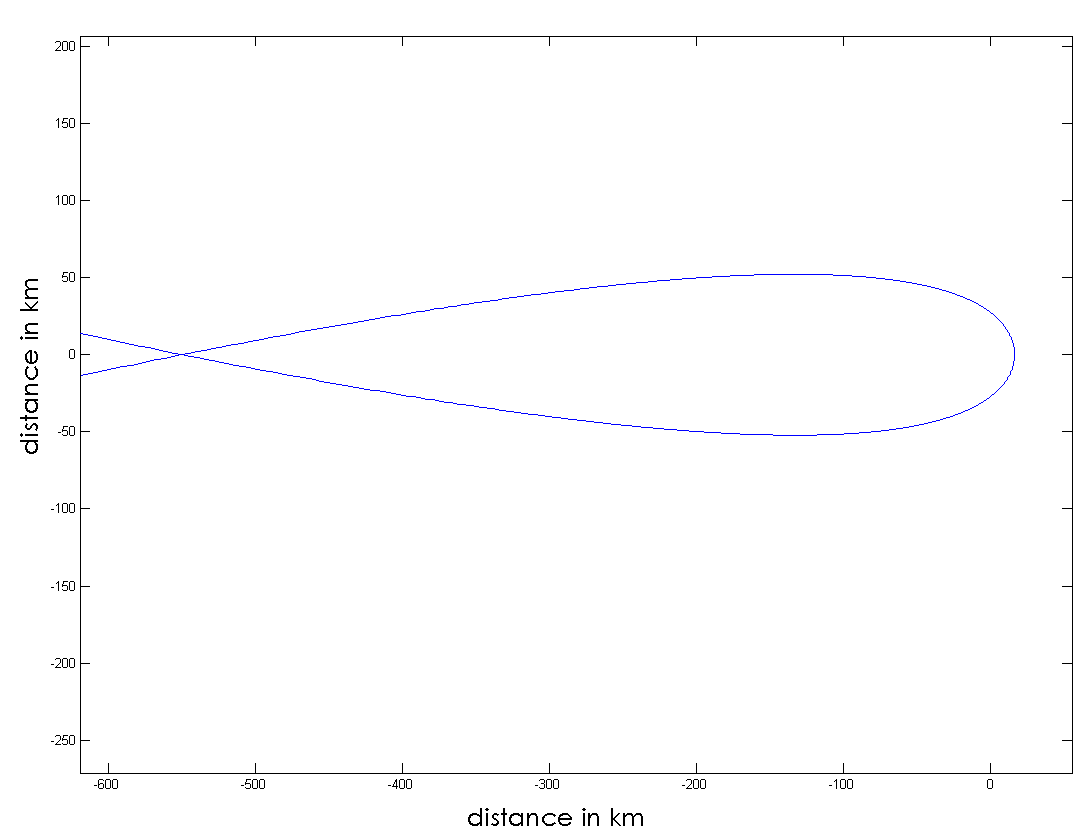
and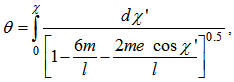

,

where all the symbols have the same meaning as in that reference. We take the values of l=8.0404m the same as that of the parabolic orbit in ref. [2]. The orbit is plotted in fig. 3 to show two successive apastrons calculated with the help of elliptic integrals as was done in my previous work. The mass of the black hole again is equal to the solar mass that is m=1.475 km.

Figure 3. Part of the orbit of a test particle which may have the mass of Mercury and in a very eccentric orbit and showing two apastrons around a black hole at the origin whose mass is that of the Sun

In order to make a more realistic study we include a parabolic orbit around a neuron star which can have a maximum mass which is 0.75 times of that of the solar mass [6]. With this value of m and l=30m, e=1 we can describe a parabolic orbit which does not collide with the neutron star and this is shown in figure 4. It is qualitatively different from a Newtonian parabola. In fig. 5 we show an expanded view of this same orbit near the origin.

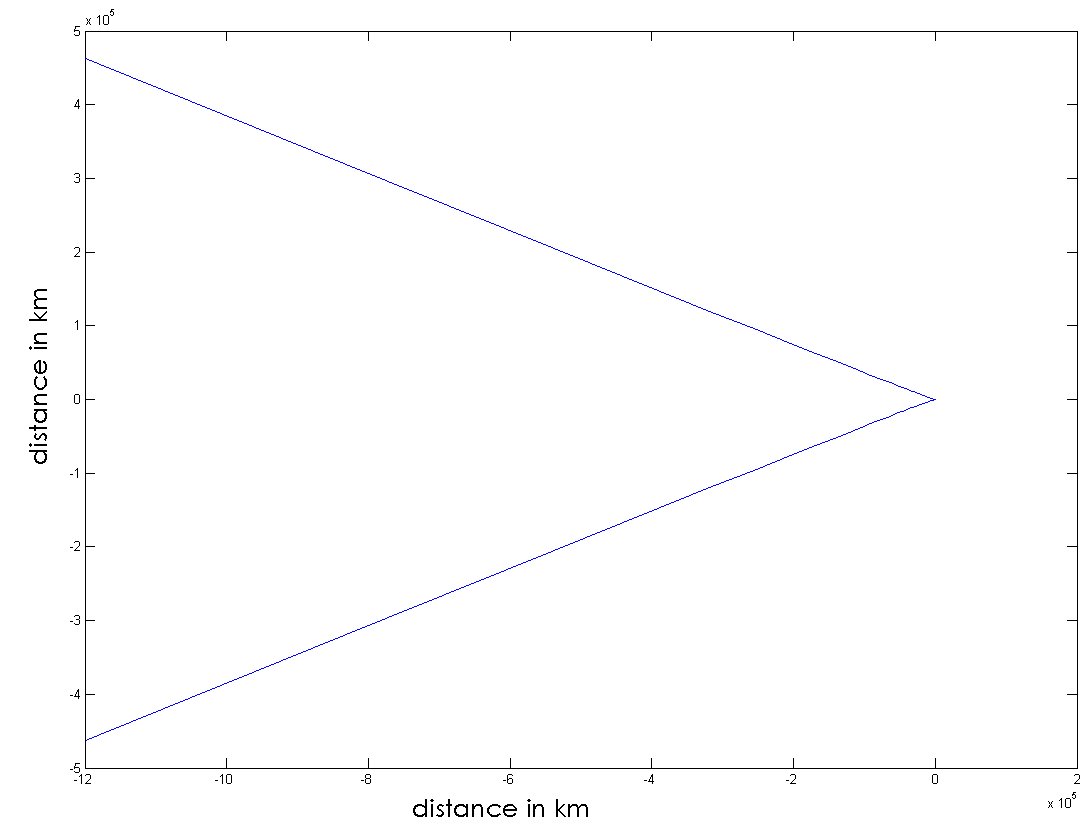Figure 4. Parabolic orbit of a test particle around a neutron star of maximum mass placed with its centre at the origin. The radius of the neutron star is at least about 10 km [7]

Figure 5. The magnified view of the orbit in figure 4 near the origin