Reza Ahangar
Department of Mathematic, Texas A & M University, Kingsville
Correspondence to: Reza Ahangar, Department of Mathematic, Texas A & M University, Kingsville.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this article, a new fundamental views on matter will be presented and the paradigm will be shifted from real or pure imaginary particle to Complex Matter Space. A new assumption will be imposed that matter has two intrinsic components, mass and charge. The mass will be measured by a real number and charge by an imaginary unit. We review some results and effects of the Complex Matter Space Theory on Special Relativity theory and hope that this approach helps a relativistic quantum view of energy and momentum in Complex Matter Space.
Keywords:
Complex Matter Space, Complex Energy, and Complex Momentum
Cite this paper: Reza Ahangar, Quantum Complex Matter Space, International Journal of Theoretical and Mathematical Physics, Vol. 4 No. 4, 2014, pp. 159-163. doi: 10.5923/j.ijtmp.20140404.04.
1. Complex Matter a New View of Imaginary Mass and Energy
In 1928, the British Physicist Paul Dirac (Dirac 2008) realized that when electrons are moving very close to the speed of light, special relativity needed to be incorporated which lead to particles with negative mass. The existence of a particle moving faster than light was presented by many authors including, Sudarshan 1970 who discussed the Physics of complex mass.The content of a paper with title "Imaginary Relativity" may be a right direction toward Complex Matter Space (CMS) but it is not for the unifying forces (Rezaei 2010). The CMS postulates may answer some of the questions in this article's concluding remarks. We postulate that matter has two components that can be demonstrated in a complex plane as a real component and an imaginary component: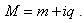 | (1.1) |
Assume that the terminology "matter" is an undefined term and we accept the following new postulate:Complex Matter SPACE (CMS) Postulate (I): mass and charge are intrinsic parts of matter and their position and rates of change of a particle can be measured and determined in a complex plane such that the real part is equal to its mass and the imaginary part is equal to the charge of the particle.Postulate (II): In a one dimensional, position and velocity are assumed to be real numbers.By accepting the second postulate of CMS we are admitting that the particle can be selected in a complex plane and the velocity of a particle can be assumed to be faster than the speed of light. The position x(t) and the speed of the particle like v=|dx/dt| will remain a real number. The speed of light remains constant c.
2. Relativistic View of the Complex Matter
Mayer 2007, designed the energy momentum in a complex plane very well without acknowledging the idea of complex matter and considering the speed of light c=1 a natural unit. Relation (1.1) can be demonstrated by Fig. (1) and in what follows we will show that the energy of a particle can be explained by Fig. (2). | Figure (1). Complex matter in a complex plane with two components (m,q) and it is denoted by M=m+iq |
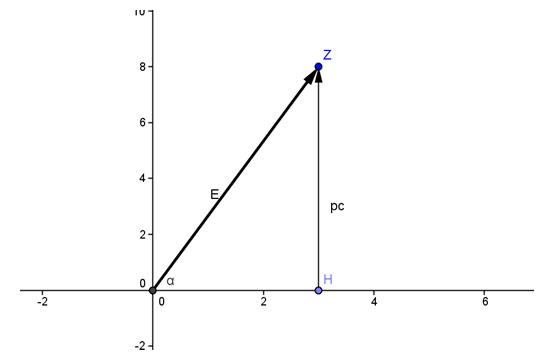 | Figure (2). Energy and Momentum in the Complex plane |
Energy in the Complex plane: A vector form of the energy is demonstrated with the horizontal component OH=mc2, and vertical component ZH=pc. The state of the energy and its magnitude can be described by 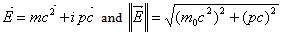 | (2.1) |
According to postulate (I), Fig.(1) and Fig.(2) demonstrate that the energy will have the two components of real and imaginary values. The energy for mass-less particles can be observed on the diagram when 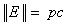 . When the real part of particle mass is not zero we will derive the energy, mass, and charge in relativistic mechanics. The norm (modulus) of the particle-like with speed faster than light can be described by
. When the real part of particle mass is not zero we will derive the energy, mass, and charge in relativistic mechanics. The norm (modulus) of the particle-like with speed faster than light can be described by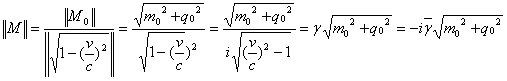 where the magnitude of particle and factor gamma is defined by:
where the magnitude of particle and factor gamma is defined by: 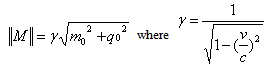 | (2.2) |
3. Derivation of Einstein Equation in Complex Matter Space
Using Postulate (I) and relation (1.1) will allow us to describe a particle-like in complex Matter Space by a set of points M(t)=m(t)+iq(t) where m is the mass and q is the charge at time t. The instantaneous rate of changes of a complex particle is denoted by 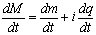 . Using special relativity theory (SRT) one can demonstrate that
. Using special relativity theory (SRT) one can demonstrate that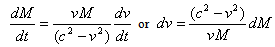 | (3.1) |
The instantaneous rate of change of energy in complex matter can be described by | (3.2) |
The State of the Energy in Complex Matter Space: According to (2.1) and (2.2) in Fig (2.1) the angle alpha can be defined by 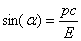 thus,
thus, 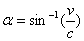 and assume
and assume 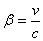 , then
, then 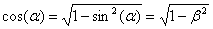 . Let us assume also
. Let us assume also 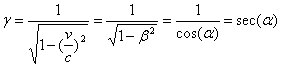 When the real part of particle mass is not zero we will derive the energy, mass, and charge in relativistic mechanics. The complex point E in Fig.(2) can be described by
When the real part of particle mass is not zero we will derive the energy, mass, and charge in relativistic mechanics. The complex point E in Fig.(2) can be described by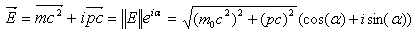 Replacing cosine and sine we will get an energy state description
Replacing cosine and sine we will get an energy state description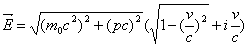 | (3.3) |
Assuming that mass of a particle is a real number when the velocity is faster than light leads us to an invalid result and this is a correction of the conclusion of a paper by (Feyman 1963, Zhang 2008, and Myer 2007). Complex Matter space is able to interpret the duality nature mass-wave characteristic of matter. We will use the complex mass magnitude to evaluate the momentum p=||M||.v 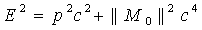 | (3.4) |
Real and Imaginary Components of Energy: Consequently energy in the complex plane can be described by the magnitude of a vector with two components 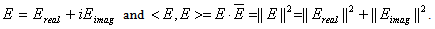 | (3.5) |
The real part of the energy can be explained by the real part of mass m. That is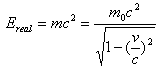 | (3.6) |
and the imaginary part of the energy will be produced by the wave characteristic of the particle, that is 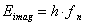 where h is the Plank constant, represents the energy of one wave and fn is the density or frequency of the particle-like photons.
where h is the Plank constant, represents the energy of one wave and fn is the density or frequency of the particle-like photons.
4. Introduction to Quantum Mechanical Views of Complex Matter Space
The following steps lead to the effects of Complex Matter theory on elementary Quantum Mechanics.It is well known that the energy of photon can be calculated if we assume that light is composed of particles. The energy is proportional to the density of the photons particles, that is1) Photon is a complex particle with zero mass. Energy of a package of photon particles is equal to energy of each particle multiply by the number of particles (frequency), that is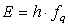 | (4.1) |
where h is the Plank constant real number. The momentum can be calculated using2) Campton Effect when particle - like is a wave. Momentum of the of the photon wave will be equal to Energy /speed, that is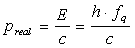 | (4.2) |
By considering velocity is equal to the frequency multiplied by the wave length, and 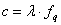 we will describe the momentum propagation of the photons as a wave by
we will describe the momentum propagation of the photons as a wave by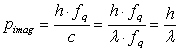 | (4.3) |
3) Using de Broglie’s Law we can find the energy of the wave (by4.1) and replacing the frequency fq is equal to the energy of the mass, that is 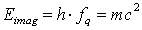 Wave length
Wave length 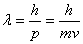 This relation has singularity for mass less particles like photons where m=0 and we can assume that the velocity is not bounded. When the velocity is zero, the wave length will be infinity which is a line with zero frequency. Mayer 2007, also has a good start on considering Energy-Momentum model in complex plane. But it does not consider matter in a complex plane. Readers may see the differences in the results. The analysis of "The Manifestation of matter waves" is done on the real line. This is a particular case which demonstrates that the phase velocity is equal to the speed of light. Combining
This relation has singularity for mass less particles like photons where m=0 and we can assume that the velocity is not bounded. When the velocity is zero, the wave length will be infinity which is a line with zero frequency. Mayer 2007, also has a good start on considering Energy-Momentum model in complex plane. But it does not consider matter in a complex plane. Readers may see the differences in the results. The analysis of "The Manifestation of matter waves" is done on the real line. This is a particular case which demonstrates that the phase velocity is equal to the speed of light. Combining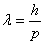 and
and 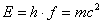 implies that:
implies that: 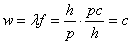 The wave frequency can be interpreted by
The wave frequency can be interpreted by 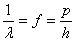 . This relation can also be extend to the Einstein mass-energy equivalence
. This relation can also be extend to the Einstein mass-energy equivalence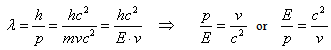 | (4.4) |
Let E=mv2/2 and it is clear that dE/dt =mv=p. We use (4.4) to modify our definition of the angle alpha in (Fig.2): 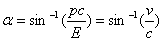 .
.
5. Momentum in Complex Matter Space
If the charge in wave-like particle is zero then dividing the real part of energy by ral part momentum will produce the following relations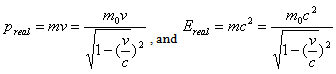 | (5.1) |
and we obtain 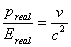 which implies the relative velocities
which implies the relative velocities 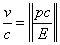 .Using Fig.(1) and the relation (2.2)
.Using Fig.(1) and the relation (2.2) 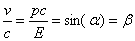 | (5.2) |
The State of the Complex Matter: Using relations (5.2), one can find the value of gamma from (2.2)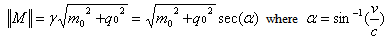 | (5.3) |
State of the Complex Energy: The complex point E can be described in the following state of energy in the complex model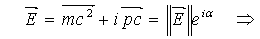
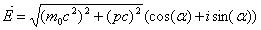 | (5.4) |
Thus, from the relation (2.1) one can conclude the real and imaginary components of energy to be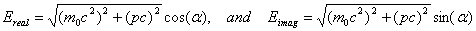 | (5.5) |
The State of the Momentum of Complex Matter: Assume that M0=(m0,q0) represents the rest point at the initial time with two components. According to postulate (II), a moving particle in complex plane at the speed 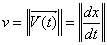 on the one dimensional x-axis, will be a real function of time. The momentum at time t can be described by
on the one dimensional x-axis, will be a real function of time. The momentum at time t can be described by 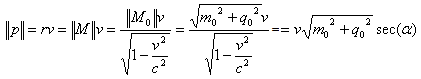 | (5.6) |
Since the wave length is 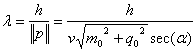 | (5.8) |
6. Conclusions
The ratio between the energy density (in Joules) and the mass density (in kg/m3) are proportional to the square of the speed of light (Guthier 2009).Recent observations by NASA agree that dark energy and dark matter have almost the same density 10-26kg/m3. A mathematical model unifying perfect fluid, Boltzman Ideal gas, and Einstein energy-mass principle may be used similarly to explain Dark energy and Dark Matter (see Shibili 2006-[12]). The new Complex Matter postulate presented in this paper is the core foundation of this research. It was shown that some modification is consistent with Newtonian, relativistic, and quantum mechanics. For speed less than the speed of light (v < c) similar modification demonstrates that the theory of complex matter is consistent with the Special Theory of Relativity. But if the speed is faster than light all relations and interpretations will be changed. In complex matter space, the state of energy and momentum and their magnitudes are presented in this paper. Consequently, Newton's Law, energy, and momentum need to be explained with this new definition of matter.
References
| [1] | Ahangar 2014, Reza R. Ahangar, “Foundation of Complex Matter Space and Special Theory of Relativity”, IOP Publishing, Report on Progress in Physics, submitted July 2014. |
| [2] | Dirac 1928, P.A.M. Dirac, "The Quantum Theory of Electron", Proc. R. Soc. A117, 610-624, p.619. |
| [3] | Feynman 1963, Richard Feynman, The Feynman Lectures on Physics (Addison Wesley, Reading, MA, 1963) Vol III, pp. 1-6, 7-5. |
| [4] | Gauthier 2009, Richard Gauthier, "The Dirac Equation and the Superluminal Electron Model",http://www.superluminalquantum.org, 2009. |
| [5] | Rezaei Mehran, "Imaginary Relativity", WSEAS TRANSACTION on COMMUNICATIONS, Issue 2, Volume 9, Feb. 2010, ISSN: 1109-2742, Esfahan Azad University, IRAN. |
| [6] | Mayer 2007, Alexander Franklin Mayer: "Wave Energy in Quantum Mechanics", Journal of Physics, Conference Series 70 (2007) 012013, IOP Publication:http://iopscience.iop.org/1712-6596/70/1/02013. |
| [7] | Shibili 2006, Murad Shibili, "The Equation of State of Dark Energy and Dark Matter: Boltzmann Constant and Unified Entity: The Utilization of Space Energy", College of Engineering, American University of Shrjeh, United Arab Emirates. |
| [8] | Shibili 2007, Murad Shibili: "The Foundations of the Fourth Law of Thermodynamics: Universe Dark Energy and Its Nature; Can Dark Energy be Generated?", International Conference on Renewable Energies and Power Quality, Seville Spain, March 26th-28th, 2007,http://www.icrepq.com/icrepq07/286-shibli.pdf. |
| [9] | Sudarshan 1969, Sudarshan, E.C.G, "A New Formulation of Relativistic Quantum Theory of Fields with Applications to particles Traveling Faster than Light", Proc. Nobel Symposium on Elementary Particle Theory. Stockholm (1968). Also Proc. Indian Academy of Science 69A, 133 (1969). |
| [10] | Sudarshan 1970, Sudarshan, E.C.G, "Physics of Complex Mass Particles", Center for Particle Theory, Department of Physics, University of Texas, Austin TexasORO-3992-5, UT-26-0823-5, Jan. 1970. |
| [11] | Umul 2007, Yousef Z. Umul, "Proof that the de Broglie-Einstein velocity equation is valid for the Non-relativistic case", the General Science Journal, www.GSJournal.net, arXiv:0712.0967v1. |
| [12] | Zhang 2008, Zhang Tianxi, "Electric Charge as a form of Imaginary Energy", Progress in Physics, vol.2, 2008. |

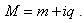


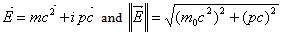
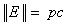 . When the real part of particle mass is not zero we will derive the energy, mass, and charge in relativistic mechanics. The norm (modulus) of the particle-like with speed faster than light can be described by
. When the real part of particle mass is not zero we will derive the energy, mass, and charge in relativistic mechanics. The norm (modulus) of the particle-like with speed faster than light can be described by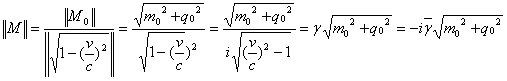 where the magnitude of particle and factor gamma is defined by:
where the magnitude of particle and factor gamma is defined by: 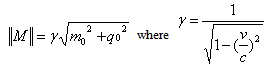
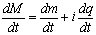 . Using special relativity theory (SRT) one can demonstrate that
. Using special relativity theory (SRT) one can demonstrate that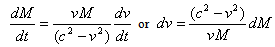

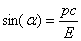 thus,
thus, 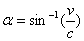 and assume
and assume 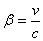 , then
, then 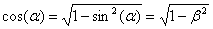 . Let us assume also
. Let us assume also 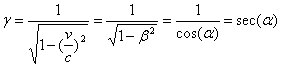 When the real part of particle mass is not zero we will derive the energy, mass, and charge in relativistic mechanics. The complex point E in Fig.(2) can be described by
When the real part of particle mass is not zero we will derive the energy, mass, and charge in relativistic mechanics. The complex point E in Fig.(2) can be described by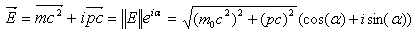 Replacing cosine and sine we will get an energy state description
Replacing cosine and sine we will get an energy state description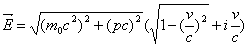
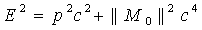
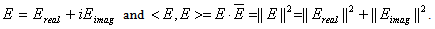
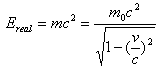
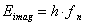 where h is the Plank constant, represents the energy of one wave and fn is the density or frequency of the particle-like photons.
where h is the Plank constant, represents the energy of one wave and fn is the density or frequency of the particle-like photons.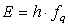
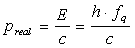
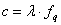 we will describe the momentum propagation of the photons as a wave by
we will describe the momentum propagation of the photons as a wave by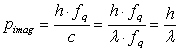
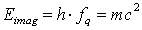 Wave length
Wave length 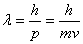 This relation has singularity for mass less particles like photons where m=0 and we can assume that the velocity is not bounded. When the velocity is zero, the wave length will be infinity which is a line with zero frequency. Mayer 2007, also has a good start on considering Energy-Momentum model in complex plane. But it does not consider matter in a complex plane. Readers may see the differences in the results. The analysis of "The Manifestation of matter waves" is done on the real line. This is a particular case which demonstrates that the phase velocity is equal to the speed of light. Combining
This relation has singularity for mass less particles like photons where m=0 and we can assume that the velocity is not bounded. When the velocity is zero, the wave length will be infinity which is a line with zero frequency. Mayer 2007, also has a good start on considering Energy-Momentum model in complex plane. But it does not consider matter in a complex plane. Readers may see the differences in the results. The analysis of "The Manifestation of matter waves" is done on the real line. This is a particular case which demonstrates that the phase velocity is equal to the speed of light. Combining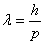 and
and 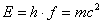 implies that:
implies that: 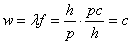 The wave frequency can be interpreted by
The wave frequency can be interpreted by 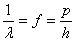 . This relation can also be extend to the Einstein mass-energy equivalence
. This relation can also be extend to the Einstein mass-energy equivalence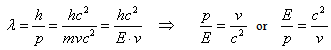
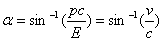 .
.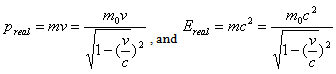
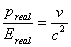 which implies the relative velocities
which implies the relative velocities 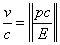 .Using Fig.(1) and the relation (2.2)
.Using Fig.(1) and the relation (2.2) 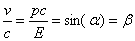
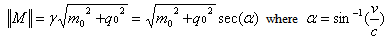
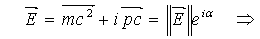
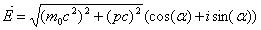
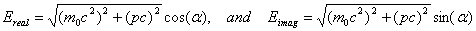
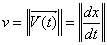 on the one dimensional x-axis, will be a real function of time. The momentum at time t can be described by
on the one dimensional x-axis, will be a real function of time. The momentum at time t can be described by 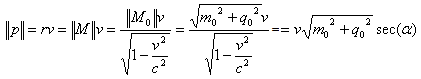
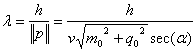
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML