V. N. Soshnikov
Plasma Physics Dept., All-Russian Institute of Scientific and Technical Information, of the Russian Academy of Sciences, VINITI, Usievitcha 20, 125315 Moscow, Russia
Correspondence to: V. N. Soshnikov, Plasma Physics Dept., All-Russian Institute of Scientific and Technical Information, of the Russian Academy of Sciences, VINITI, Usievitcha 20, 125315 Moscow, Russia.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Damping/growing of electron waves in collisionless plasmas (kinetic equation with zero collision terms) does not exist contrary to the established among plasma physicists more than half a century ago the view about theoretical discovery of its existence as a natural and experimentally confirmed physical phenomenon.
Keywords:
Electron waves in collisionless plasma, Plasma waves damping/growing
Cite this paper: V. N. Soshnikov, Replay: On a Common Logical Error in Calculation and Applying the Complex Conductivities of Collisionless Plasmas, International Journal of Theoretical and Mathematical Physics, Vol. 4 No. 4, 2014, pp. 156-158. doi: 10.5923/j.ijtmp.20140404.03.
1. Commentary
The recent discussion [1-4] (with not principal amendment in improper integral (18) in [2] ) clearly confirms the trivial logical (and ultimately mathematical) cause of widespread (see e.g. textbooks [5-7] and numerous in literature other articles and textbooks on plasma physics) erroneous description of non-existing collisionless damping of waves in both non-magnetoactive and in general case magnetoactive collisionless (in the sense of neglecting the collision energy-exchange terms in kinetic equation) plasmas. The reason is that all the quantitative laws of the nature are characterized as relations between the so-called physically detectable values (PhDVs), which in the case of their complex representation (before all further non-linear complex transformations!) have to be substituted into the real initial wave equations in the form of real combinations of complex conjugate sets as it is done, for example, in the form of direct substitution of sought PhDVs into the wave equations in the works [1-4] with the final results also in the natural form of relations real PhDVs. Moreover, a direct unambiguous relation is derived between the wave damping/growing parameters (if present) with the defined collision terms of kinetic equation.It is wrong, for example, using generalization to damping/growing plasma waves by moving on to a complex wave number 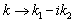 in the intermediate steps or the final result (in the form of the dispersion equation) in the case of a real
in the intermediate steps or the final result (in the form of the dispersion equation) in the case of a real 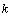 , because in complex nonlinear equations mixing occurs of terms with
, because in complex nonlinear equations mixing occurs of terms with 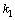 and
and 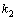 in the imaginary and real parts of the resulting complex equations and expressions, and it becomes impossible to extract from them the true relations between PhDVs. In these cases, there arise also wrong side complex roots of the dispersion equation and a variety of side terms of complex expressions ("spirits"). It is absolutely wrong detection the true relations of PhDVs by separating the real part of final complex dispersion equation with dropping the imaginary part [2] which leads to collisional damping.A typical case is nonlinear with respect to combinations of
in the imaginary and real parts of the resulting complex equations and expressions, and it becomes impossible to extract from them the true relations between PhDVs. In these cases, there arise also wrong side complex roots of the dispersion equation and a variety of side terms of complex expressions ("spirits"). It is absolutely wrong detection the true relations of PhDVs by separating the real part of final complex dispersion equation with dropping the imaginary part [2] which leads to collisional damping.A typical case is nonlinear with respect to combinations of 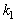 and
and 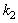 resulting dispersion equation with complex wave functions in the initially linear wave equations. And it is due to initial complex nonlinearity between combinations of the real and imaginary values. Сomplex nonlinearity arises, for example, in the simplest case of derivative
resulting dispersion equation with complex wave functions in the initially linear wave equations. And it is due to initial complex nonlinearity between combinations of the real and imaginary values. Сomplex nonlinearity arises, for example, in the simplest case of derivative 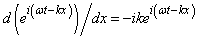 at complex
at complex 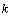 with its corresponding inequalities at extending
with its corresponding inequalities at extending 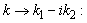 as an arbitrary but typical illustrative simple example of possible mixing real and imaginary parts in final real expressions (cf. also complex conjugated sums (13) with mixing real and imaginary terms):
as an arbitrary but typical illustrative simple example of possible mixing real and imaginary parts in final real expressions (cf. also complex conjugated sums (13) with mixing real and imaginary terms):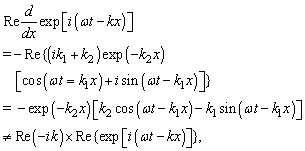 | (1) |
i.e. there are inadmissible anyway generalizations in the transition from real to complex 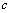 and
and 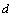 of the type
of the type 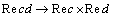 (cf. also below Eq. (13)).It is rather unclear how to allocate the true relation between the sought real PhDVs after transformations to final complex dispersion equation with complex wave functions for the case of the usual complex wave functions with the damping
(cf. also below Eq. (13)).It is rather unclear how to allocate the true relation between the sought real PhDVs after transformations to final complex dispersion equation with complex wave functions for the case of the usual complex wave functions with the damping 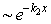 :
: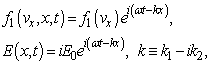 | (2) |
unlike initial substitutionin real form: 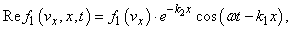 | (3) |
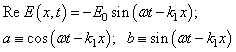 | (4) |
where 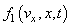 is perturbation of the background electron Maxwellian function
is perturbation of the background electron Maxwellian function 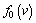 ;
; 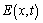 is the field perturbation from external field
is the field perturbation from external field 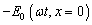 .Substituting real expressions (3) and (4) into real wave equations (kinetic and Maxwell equation)
.Substituting real expressions (3) and (4) into real wave equations (kinetic and Maxwell equation)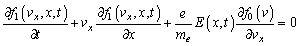 | (5) |
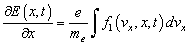 | (6) |
where 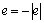 is electron charge,
is electron charge, 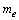 is electron mass and
is electron mass and 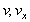 are electron velocities, leads to the real dispersion relation [1], [2]:
are electron velocities, leads to the real dispersion relation [1], [2]: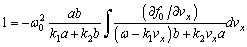 | (7) |
where 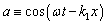 ,
, 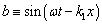 ,
, 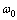 is Langmuir frequency
is Langmuir frequency 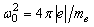 . It means that hypothetical solutions of Eq. (7) with
. It means that hypothetical solutions of Eq. (7) with 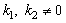 that would not depend on
that would not depend on 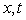 do not exist. However, one can try to get some average values
do not exist. However, one can try to get some average values 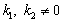 over the wave period introducing the collision term
over the wave period introducing the collision term 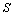 on the right hand side of the kinetic equation with the dispersion equation of the form
on the right hand side of the kinetic equation with the dispersion equation of the form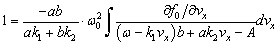 | (8) |
taking 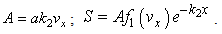 | (9) |
In this case dispersion relation takes the form [1], [2]: 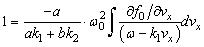 ;
;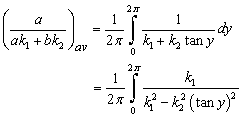 | (10) |
with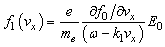 | (11) |
where all integrals can be taken, including improper integrals (10), in the principal value sense. Besides that, due to singularity of the function 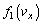 at the point
at the point 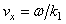 in Eq. (11) near which the kinetic equation does not apply, it is necessary cutting off
in Eq. (11) near which the kinetic equation does not apply, it is necessary cutting off 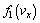 in (11) nearby this point in accordance with the condition of positivity the total distribution function
in (11) nearby this point in accordance with the condition of positivity the total distribution function 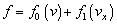 :
: 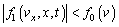 | (12) |
The results obtained are in principle different from those obtained when ubiquitous, without any exceptions, using the dispersion equations in the case 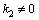 after substitution therein complex wave functions (2) (see [1]). In this case, the complex roots of the dispersion equation contain an artifact when appearing imaginary part due to mixed, real and imaginary terms with
after substitution therein complex wave functions (2) (see [1]). In this case, the complex roots of the dispersion equation contain an artifact when appearing imaginary part due to mixed, real and imaginary terms with 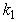 and
and 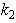 entails respectively two equations for the real and imaginary parts of dispersion equation that does not correspond in no way to the law of energy conservation or any other physical law. In contrast, the real dispersion equation is single equation containing both parameters
entails respectively two equations for the real and imaginary parts of dispersion equation that does not correspond in no way to the law of energy conservation or any other physical law. In contrast, the real dispersion equation is single equation containing both parameters 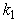 and
and 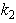 , while the second equation of the system for to find
, while the second equation of the system for to find 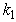 and
and 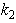 is directly the new second equation of energy conservation that independently binds the sought parameters
is directly the new second equation of energy conservation that independently binds the sought parameters 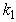 and
and 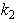 included in collisional energy-exchange terms
included in collisional energy-exchange terms 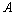 and
and 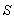 according to (9) (see, for example, [1], [2], where also are pointed out numerous contradictions of the so-called collisionless damping in the current formulation of the problem). From the above, it also follows that the commonly used expressions for complex tensors of electrical conductivity and dielectric permittivity of collisionless plasma should be used directly only for the real
according to (9) (see, for example, [1], [2], where also are pointed out numerous contradictions of the so-called collisionless damping in the current formulation of the problem). From the above, it also follows that the commonly used expressions for complex tensors of electrical conductivity and dielectric permittivity of collisionless plasma should be used directly only for the real 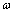 and
and 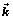 or with substitution of initially complex conjugate expressions for PhDVs which significantly reduces the advantages of using сomplex variables.Use of complex wave functions can lead to complex dispersion equations with complex non-physical roots. The analytical mathematical formalism of complex tensor conductivity/permeability is inapplicable in the presence of any significant energy exchange processes, with rather non-sinusoidal form of propagating waves.In general, the solution for PhDVs can be obtained by using the complex conductivity tensor
or with substitution of initially complex conjugate expressions for PhDVs which significantly reduces the advantages of using сomplex variables.Use of complex wave functions can lead to complex dispersion equations with complex non-physical roots. The analytical mathematical formalism of complex tensor conductivity/permeability is inapplicable in the presence of any significant energy exchange processes, with rather non-sinusoidal form of propagating waves.In general, the solution for PhDVs can be obtained by using the complex conductivity tensor 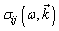 with
with 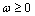 and complex
and complex 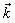 as a real solution of the dispersion equation of the form
as a real solution of the dispersion equation of the form 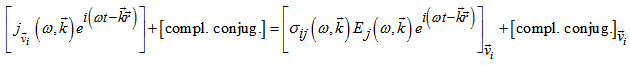 | (13) |
which should be followed by integration over 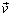 , where
, where 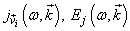 are complex components of integral Fourier expansion correspondingly for electrical current and tension of electrical field. In this approach, the consideration of imaginary part of such form of dispersion equation which should lead to the collisionless damping becomes meaningless.Thus, in general, the real dispersion equation and its solution may contain the angular coordinates of the real and imaginary parts of the initial wave function with
are complex components of integral Fourier expansion correspondingly for electrical current and tension of electrical field. In this approach, the consideration of imaginary part of such form of dispersion equation which should lead to the collisionless damping becomes meaningless.Thus, in general, the real dispersion equation and its solution may contain the angular coordinates of the real and imaginary parts of the initial wave function with 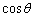 and
and 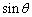 , which makes however impossible to use the solution of dispersion equation (cf. (7)).In the derivation of Eq.(13) it was assumed solution in the form of Fourier transform
, which makes however impossible to use the solution of dispersion equation (cf. (7)).In the derivation of Eq.(13) it was assumed solution in the form of Fourier transform 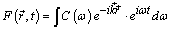 with one-valued dependence
with one-valued dependence 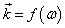 at general case of complex
at general case of complex 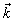 . But in general, solutions have form of the double (in
. But in general, solutions have form of the double (in 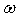 and
and 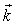 ) Fourier transform
) Fourier transform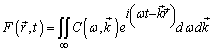 | (14) |
with real 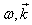 , and such one-valued dependence
, and such one-valued dependence 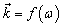 can be not existing, i.e. to each
can be not existing, i.e. to each 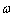 there corresponds the whole spectrum of values
there corresponds the whole spectrum of values 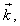 and solutions of the form
and solutions of the form 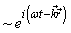 of the type (13) with complex
of the type (13) with complex 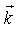 do not exist at all (as evidenced by the above example of the dispersion equation (7) ). Also very relation (13) becomes invalid.Moreover, theoretical contradictions are accompanied with poorly compatible conditions of proposed experiments on collisionless damping (1).
do not exist at all (as evidenced by the above example of the dispersion equation (7) ). Also very relation (13) becomes invalid.Moreover, theoretical contradictions are accompanied with poorly compatible conditions of proposed experiments on collisionless damping (1).
2. Conclusions
Using a two-parametric 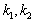 non-physical complex root of the complex dispersion equation for damping complex plasma waves in a collisionless plasma instead of detecting the two real observable parameters of the real dispersion equation with adding two-parametric real energy conservation equation is common fundamental logical and, by inference, mathematical error available in the literature on Plasma Physics, which leads to an erroneous conclusion about the existence of collisionless damping of plasma waves with derived non physical decrement.Procedure (13) of the transition to real dispersion equation complemented by integration over
non-physical complex root of the complex dispersion equation for damping complex plasma waves in a collisionless plasma instead of detecting the two real observable parameters of the real dispersion equation with adding two-parametric real energy conservation equation is common fundamental logical and, by inference, mathematical error available in the literature on Plasma Physics, which leads to an erroneous conclusion about the existence of collisionless damping of plasma waves with derived non physical decrement.Procedure (13) of the transition to real dispersion equation complemented by integration over 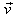 entirely changes the normal procedure for the application of the complex conductivity tensor of collisionless and collision plasma and can lead to in principle different from existing dispersion equations and their solutions with appearing collisionless damping.Exponentially damping sinusoidal plasma wave solutions for both collisionless and collision plasma do not exist.
entirely changes the normal procedure for the application of the complex conductivity tensor of collisionless and collision plasma and can lead to in principle different from existing dispersion equations and their solutions with appearing collisionless damping.Exponentially damping sinusoidal plasma wave solutions for both collisionless and collision plasma do not exist.
References
| [1] | Soshnikov V. N., Logical contradictions of Landau damping. Arxiv.org/physics/0610220, pp. 1 – 30. |
| [2] | Soshnikov V. N., On the wave damping in weakly collision plasma. International Journal of Theoretical and Mathematical Physics, 2014; 4(2), pp. 58-62. |
| [3] | Soshnikov V. N., Solving non-linear equations of longitudinal and transverse electron waves in collisionless Maxwellian plasma. ArXiv.org/physics/0711.1321, pp. 1 - 11. |
| [4] | Soshnikov V. N., Solving non-linear equations of longitudinal and transverse electron waves in collisionless Maxwellian plasma. International Journal of Theoretical and Mathematical Physics, 2014; 4(3), pp. 134 – 141. |
| [5] | Frank-Kamenetsky D. A. Лекции по физике плазмы. (Lectures on Plasma Physics, in Russian). Atomizdat, M, 2nd ed., Москва, 1968, 281 с. (281 pp.). |
| [6] | Lifshitz E. M., Pitaevskii L. P., Physical Kinetics (Moscow, Nauka), 1979 (in Russian). See also: Lifshitz E. M., Pitaevskii L. P., Physical Kinetics. Pergamon, Oxford, 1981. |
| [7] | Alexandrov A. F., Bogdankevitch L. S., Rukhadze A. A.. Fundamentals of Plasma Electrodynamics. Moscow, Vysshaya shkola, 1988 (in Russian), 274 pp. See also: Alexandrov A.F., Bogdankevich L.S., Rukhadze A.A. Principles of Plasma Electrodynamics, Heidelberg: Springer Verlag, 1984. |

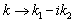 in the intermediate steps or the final result (in the form of the dispersion equation) in the case of a real
in the intermediate steps or the final result (in the form of the dispersion equation) in the case of a real 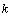 , because in complex nonlinear equations mixing occurs of terms with
, because in complex nonlinear equations mixing occurs of terms with 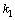 and
and 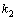 in the imaginary and real parts of the resulting complex equations and expressions, and it becomes impossible to extract from them the true relations between PhDVs. In these cases, there arise also wrong side complex roots of the dispersion equation and a variety of side terms of complex expressions ("spirits"). It is absolutely wrong detection the true relations of PhDVs by separating the real part of final complex dispersion equation with dropping the imaginary part [2] which leads to collisional damping.A typical case is nonlinear with respect to combinations of
in the imaginary and real parts of the resulting complex equations and expressions, and it becomes impossible to extract from them the true relations between PhDVs. In these cases, there arise also wrong side complex roots of the dispersion equation and a variety of side terms of complex expressions ("spirits"). It is absolutely wrong detection the true relations of PhDVs by separating the real part of final complex dispersion equation with dropping the imaginary part [2] which leads to collisional damping.A typical case is nonlinear with respect to combinations of 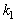 and
and 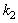 resulting dispersion equation with complex wave functions in the initially linear wave equations. And it is due to initial complex nonlinearity between combinations of the real and imaginary values. Сomplex nonlinearity arises, for example, in the simplest case of derivative
resulting dispersion equation with complex wave functions in the initially linear wave equations. And it is due to initial complex nonlinearity between combinations of the real and imaginary values. Сomplex nonlinearity arises, for example, in the simplest case of derivative 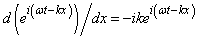 at complex
at complex 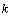 with its corresponding inequalities at extending
with its corresponding inequalities at extending 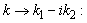 as an arbitrary but typical illustrative simple example of possible mixing real and imaginary parts in final real expressions (cf. also complex conjugated sums (13) with mixing real and imaginary terms):
as an arbitrary but typical illustrative simple example of possible mixing real and imaginary parts in final real expressions (cf. also complex conjugated sums (13) with mixing real and imaginary terms):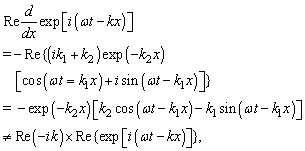
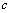 and
and 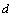 of the type
of the type 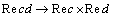 (cf. also below Eq. (13)).It is rather unclear how to allocate the true relation between the sought real PhDVs after transformations to final complex dispersion equation with complex wave functions for the case of the usual complex wave functions with the damping
(cf. also below Eq. (13)).It is rather unclear how to allocate the true relation between the sought real PhDVs after transformations to final complex dispersion equation with complex wave functions for the case of the usual complex wave functions with the damping 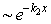 :
: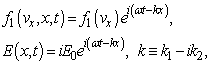
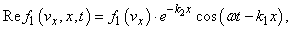
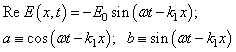
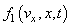 is perturbation of the background electron Maxwellian function
is perturbation of the background electron Maxwellian function 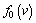 ;
; 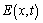 is the field perturbation from external field
is the field perturbation from external field 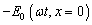 .Substituting real expressions (3) and (4) into real wave equations (kinetic and Maxwell equation)
.Substituting real expressions (3) and (4) into real wave equations (kinetic and Maxwell equation)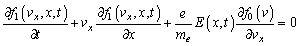
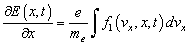
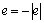 is electron charge,
is electron charge, 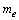 is electron mass and
is electron mass and 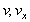 are electron velocities, leads to the real dispersion relation [1], [2]:
are electron velocities, leads to the real dispersion relation [1], [2]: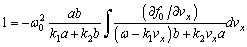
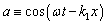 ,
, 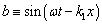 ,
, 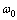 is Langmuir frequency
is Langmuir frequency 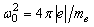 . It means that hypothetical solutions of Eq. (7) with
. It means that hypothetical solutions of Eq. (7) with 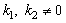 that would not depend on
that would not depend on 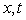 do not exist. However, one can try to get some average values
do not exist. However, one can try to get some average values 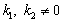 over the wave period introducing the collision term
over the wave period introducing the collision term 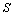 on the right hand side of the kinetic equation with the dispersion equation of the form
on the right hand side of the kinetic equation with the dispersion equation of the form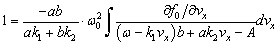
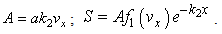
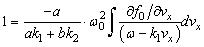 ;
;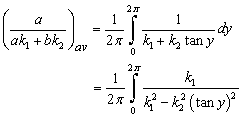
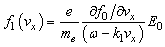
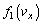 at the point
at the point 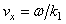 in Eq. (11) near which the kinetic equation does not apply, it is necessary cutting off
in Eq. (11) near which the kinetic equation does not apply, it is necessary cutting off 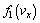 in (11) nearby this point in accordance with the condition of positivity the total distribution function
in (11) nearby this point in accordance with the condition of positivity the total distribution function 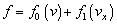 :
: 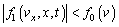
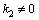 after substitution therein complex wave functions (2) (see [1]). In this case, the complex roots of the dispersion equation contain an artifact when appearing imaginary part due to mixed, real and imaginary terms with
after substitution therein complex wave functions (2) (see [1]). In this case, the complex roots of the dispersion equation contain an artifact when appearing imaginary part due to mixed, real and imaginary terms with 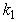 and
and 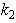 entails respectively two equations for the real and imaginary parts of dispersion equation that does not correspond in no way to the law of energy conservation or any other physical law. In contrast, the real dispersion equation is single equation containing both parameters
entails respectively two equations for the real and imaginary parts of dispersion equation that does not correspond in no way to the law of energy conservation or any other physical law. In contrast, the real dispersion equation is single equation containing both parameters 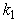 and
and 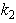 , while the second equation of the system for to find
, while the second equation of the system for to find 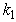 and
and 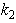 is directly the new second equation of energy conservation that independently binds the sought parameters
is directly the new second equation of energy conservation that independently binds the sought parameters 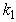 and
and 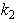 included in collisional energy-exchange terms
included in collisional energy-exchange terms 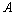 and
and 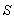 according to (9) (see, for example, [1], [2], where also are pointed out numerous contradictions of the so-called collisionless damping in the current formulation of the problem). From the above, it also follows that the commonly used expressions for complex tensors of electrical conductivity and dielectric permittivity of collisionless plasma should be used directly only for the real
according to (9) (see, for example, [1], [2], where also are pointed out numerous contradictions of the so-called collisionless damping in the current formulation of the problem). From the above, it also follows that the commonly used expressions for complex tensors of electrical conductivity and dielectric permittivity of collisionless plasma should be used directly only for the real 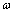 and
and 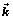 or with substitution of initially complex conjugate expressions for PhDVs which significantly reduces the advantages of using сomplex variables.Use of complex wave functions can lead to complex dispersion equations with complex non-physical roots. The analytical mathematical formalism of complex tensor conductivity/permeability is inapplicable in the presence of any significant energy exchange processes, with rather non-sinusoidal form of propagating waves.In general, the solution for PhDVs can be obtained by using the complex conductivity tensor
or with substitution of initially complex conjugate expressions for PhDVs which significantly reduces the advantages of using сomplex variables.Use of complex wave functions can lead to complex dispersion equations with complex non-physical roots. The analytical mathematical formalism of complex tensor conductivity/permeability is inapplicable in the presence of any significant energy exchange processes, with rather non-sinusoidal form of propagating waves.In general, the solution for PhDVs can be obtained by using the complex conductivity tensor 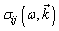 with
with 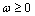 and complex
and complex 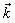 as a real solution of the dispersion equation of the form
as a real solution of the dispersion equation of the form 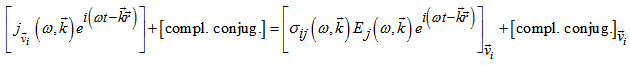
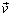 , where
, where 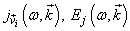 are complex components of integral Fourier expansion correspondingly for electrical current and tension of electrical field. In this approach, the consideration of imaginary part of such form of dispersion equation which should lead to the collisionless damping becomes meaningless.Thus, in general, the real dispersion equation and its solution may contain the angular coordinates of the real and imaginary parts of the initial wave function with
are complex components of integral Fourier expansion correspondingly for electrical current and tension of electrical field. In this approach, the consideration of imaginary part of such form of dispersion equation which should lead to the collisionless damping becomes meaningless.Thus, in general, the real dispersion equation and its solution may contain the angular coordinates of the real and imaginary parts of the initial wave function with 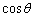 and
and 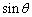 , which makes however impossible to use the solution of dispersion equation (cf. (7)).In the derivation of Eq.(13) it was assumed solution in the form of Fourier transform
, which makes however impossible to use the solution of dispersion equation (cf. (7)).In the derivation of Eq.(13) it was assumed solution in the form of Fourier transform 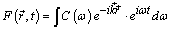 with one-valued dependence
with one-valued dependence 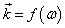 at general case of complex
at general case of complex 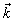 . But in general, solutions have form of the double (in
. But in general, solutions have form of the double (in 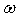 and
and 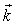 ) Fourier transform
) Fourier transform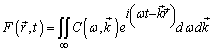
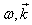 , and such one-valued dependence
, and such one-valued dependence 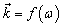 can be not existing, i.e. to each
can be not existing, i.e. to each 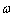 there corresponds the whole spectrum of values
there corresponds the whole spectrum of values 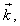 and solutions of the form
and solutions of the form 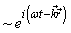 of the type (13) with complex
of the type (13) with complex 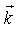 do not exist at all (as evidenced by the above example of the dispersion equation (7) ). Also very relation (13) becomes invalid.Moreover, theoretical contradictions are accompanied with poorly compatible conditions of proposed experiments on collisionless damping (1).
do not exist at all (as evidenced by the above example of the dispersion equation (7) ). Also very relation (13) becomes invalid.Moreover, theoretical contradictions are accompanied with poorly compatible conditions of proposed experiments on collisionless damping (1).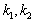 non-physical complex root of the complex dispersion equation for damping complex plasma waves in a collisionless plasma instead of detecting the two real observable parameters of the real dispersion equation with adding two-parametric real energy conservation equation is common fundamental logical and, by inference, mathematical error available in the literature on Plasma Physics, which leads to an erroneous conclusion about the existence of collisionless damping of plasma waves with derived non physical decrement.Procedure (13) of the transition to real dispersion equation complemented by integration over
non-physical complex root of the complex dispersion equation for damping complex plasma waves in a collisionless plasma instead of detecting the two real observable parameters of the real dispersion equation with adding two-parametric real energy conservation equation is common fundamental logical and, by inference, mathematical error available in the literature on Plasma Physics, which leads to an erroneous conclusion about the existence of collisionless damping of plasma waves with derived non physical decrement.Procedure (13) of the transition to real dispersion equation complemented by integration over 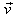 entirely changes the normal procedure for the application of the complex conductivity tensor of collisionless and collision plasma and can lead to in principle different from existing dispersion equations and their solutions with appearing collisionless damping.Exponentially damping sinusoidal plasma wave solutions for both collisionless and collision plasma do not exist.
entirely changes the normal procedure for the application of the complex conductivity tensor of collisionless and collision plasma and can lead to in principle different from existing dispersion equations and their solutions with appearing collisionless damping.Exponentially damping sinusoidal plasma wave solutions for both collisionless and collision plasma do not exist.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML