John Kulick
University of Connecticut, Connecticut, USA
Correspondence to: John Kulick , University of Connecticut, Connecticut, USA.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Abstract
If the inertial properties of matter diminished according to 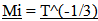 , with a corresponding loss of intrinsic energy, (The “_” notation represents a ratio of past measures over present measures so
, with a corresponding loss of intrinsic energy, (The “_” notation represents a ratio of past measures over present measures so 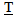 represents the ratio of the objects location in Cosmological Time divided by the Age of the Universe, and
represents the ratio of the objects location in Cosmological Time divided by the Age of the Universe, and 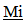 represents a ratio of the past over the present measures of inertial mass), then some interesting relationships result and a number of fundamental ambiguities in physics are resolved. Mentioning just one ambiguity; a gram of matter and a gram of radiant energy in intergalactic space now would maintain their equivalency over time, even though the photon loses energy as evidenced by the Cosmological Red Shift. As inertial mass is lost, relationships defined by a balance between inertial and spatial forces contract. (Spatial Forces are defined by spatial field based relationships associated with Gravity and Electromagnetism.) Spectra emitted or absorbed in the past would be “redder” than spectra produced in the present due to the denser atomic electrostatic field relationships in the present compared to the past. The contraction of atomic relationships also contracts local rulers which results in a measured Cosmological Red Shift that varies by
represents a ratio of the past over the present measures of inertial mass), then some interesting relationships result and a number of fundamental ambiguities in physics are resolved. Mentioning just one ambiguity; a gram of matter and a gram of radiant energy in intergalactic space now would maintain their equivalency over time, even though the photon loses energy as evidenced by the Cosmological Red Shift. As inertial mass is lost, relationships defined by a balance between inertial and spatial forces contract. (Spatial Forces are defined by spatial field based relationships associated with Gravity and Electromagnetism.) Spectra emitted or absorbed in the past would be “redder” than spectra produced in the present due to the denser atomic electrostatic field relationships in the present compared to the past. The contraction of atomic relationships also contracts local rulers which results in a measured Cosmological Red Shift that varies by 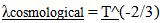 This establishes an alternative or additional explanation for the observed Recessional Red shift. Clock rates established by a balance between inertial and spatial forces speed up over time so intervals of time to vary by,
This establishes an alternative or additional explanation for the observed Recessional Red shift. Clock rates established by a balance between inertial and spatial forces speed up over time so intervals of time to vary by, 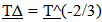 , which also produces an alternative or additional explanation for Time Dilation. The hypothetical geometrically defined model that could yield this variation in inertial mass is based on the following assumptions; 1. An extra dimensional space, (or Unobserved Space, or a set of extra dimensionally defined spatial field relationships), is in motion and is passing through our Observable Space. 2. It is the velocity of Unobserved Space through matter that imparts to mass the properties of inertia and “intrinsic” energy (E = mcc). 3. Unobserved Space and Observable Space are geometrically interconnected and are expanding at the same geometrically defined rate of
, which also produces an alternative or additional explanation for Time Dilation. The hypothetical geometrically defined model that could yield this variation in inertial mass is based on the following assumptions; 1. An extra dimensional space, (or Unobserved Space, or a set of extra dimensionally defined spatial field relationships), is in motion and is passing through our Observable Space. 2. It is the velocity of Unobserved Space through matter that imparts to mass the properties of inertia and “intrinsic” energy (E = mcc). 3. Unobserved Space and Observable Space are geometrically interconnected and are expanding at the same geometrically defined rate of 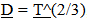 , where
, where 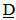 refers to the proportional distance between points on the spatial field. 4. The velocity of Unobserved Space, Vu, is diminished at a geometrically derived rate of
refers to the proportional distance between points on the spatial field. 4. The velocity of Unobserved Space, Vu, is diminished at a geometrically derived rate of 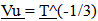 which results in the property of inertia to vary at the same rate. The model is called the “Vu model”. Analogously, just as we can visualize an expanding “flatland universe” in motion along an unobserved orthogonal dimension, we can visualize it instead as an Unobserved Space passing through a Flatland Universe. The same “rules” that were developed in a previous Paper, (A Multidimensional Geometric Expansion of Spacetime) [2] that established the geometric expansion of Observable Space also apply within Unobserved Space. This is the second of 4 papers that together define an alternative geometry for Spacetime and the Cosmos. The four papers together will establish a model that apparently will not need Dark Matter or Dark Energy to be consistent with the cosmological locations and rotational rates of Galaxies in the Universe.
which results in the property of inertia to vary at the same rate. The model is called the “Vu model”. Analogously, just as we can visualize an expanding “flatland universe” in motion along an unobserved orthogonal dimension, we can visualize it instead as an Unobserved Space passing through a Flatland Universe. The same “rules” that were developed in a previous Paper, (A Multidimensional Geometric Expansion of Spacetime) [2] that established the geometric expansion of Observable Space also apply within Unobserved Space. This is the second of 4 papers that together define an alternative geometry for Spacetime and the Cosmos. The four papers together will establish a model that apparently will not need Dark Matter or Dark Energy to be consistent with the cosmological locations and rotational rates of Galaxies in the Universe.
Keywords:
Inertia, Alternative Cosmological Red Shift, Time Dilation, Extra Dimensions of Space, Diminishing Inertial Mass over Cosmological Time, a geometric multidimensional expansion of Spacetime
Cite this paper: John Kulick , Could the Inertia and Energy Content of Matter Diminish over Cosmological Time?[1], International Journal of Theoretical and Mathematical Physics, Vol. 4 No. 3, 2014, pp. 120-133. doi: 10.5923/j.ijtmp.20140403.08.
1. Introduction – Inertial Mass
The inertial mass of an object and the gravitational mass of the object has been directly correlated; double the mass, and the gravitational effect doubles. The classic experiments of Lord Cavendish in the late 1800’s [3] and Loránd Eötvös’s in the early 1900’s [4] provided the proof of this equivalency. Eotvos’s response to this revelation was “happiness” [5]. Two seemingly different physical responses of mass, a gravitational effect and an inertial effect, appear to be equal to each other. Einstein’s 1916 paper on General Relativity is even based on this equivalency principal [6]. Proposing that inertial mass varies over Cosmological periods may seem to violate the one or more of the fundamental principles of physics. Actually, the proposed variation in inertial mass preserves or restores one of the foundations of physics, the equivalency between matter and radiant energy over time. Locally the equality can be assumed with no loss of accuracy or destruction of locally established principles. A broader term of Spatial Mass will be used instead of gravitational mass to include electromagnetic field effects.If the loss of inertial mass were to occur at a very specifically defined rate over Cosmological time, a number of interesting relationships can be established associated with the Cosmological Red Shift, and Cosmological Dilation, both Temporal and Spatial. Also, a fundamental ambiguity involving the application of General Relativity to Cosmology becomes resolved.
1.1. Outline
The first number generally corresponds to a specific topic or chapter. The second number defines sections within the chapter. 1. Introduction – Inertial Mass1.1. Outline 1.2. Second of Four Papers1.3. Reason for model – A Cosmological Red Shift and Dilation1.4. Resolving “Mainstream” Ambiguities1.5. Heading, Figure, Equation Designations and Notation1.6. Similar Proposal by Another Person2. Spatial and Inertial Mass2.1. “Mainstream” Equivalency Assumed2.2. Equivalency challenged, not Relativity2.3. Justification of Equivalency based on Stability2.4. Spatial Mass2.5. Inertial Mass2.6. Building Blocks3. Diminishing Inertial Mass, 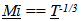 3.1. Balancing Forces in Dynamic Systems and Collapsing Orbits3.2. The Relationships of Collapsing Orbits 3.3. Smaller Orbital Periods and Faster Clock Rates 3.4. Shrinking rulers3.5. Radial acceleration (Not Dark Matter)4. Local and Cosmological measures4.1. Local Measures4.2. Cosmological measures 4.3. Dilation Effects Restored (Mostly)5. Cosmological Red Shift 5.1. Energy variation over cosmological time5.2. Cosmological red shift,
3.1. Balancing Forces in Dynamic Systems and Collapsing Orbits3.2. The Relationships of Collapsing Orbits 3.3. Smaller Orbital Periods and Faster Clock Rates 3.4. Shrinking rulers3.5. Radial acceleration (Not Dark Matter)4. Local and Cosmological measures4.1. Local Measures4.2. Cosmological measures 4.3. Dilation Effects Restored (Mostly)5. Cosmological Red Shift 5.1. Energy variation over cosmological time5.2. Cosmological red shift, 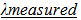 6. Fundamental Issues Resolved6.1. “Mainstream model fix”6.2. Resolving Issues for the GEM from the First Paper7. Development of the Vu Model7.1. Caution, Unconventional7.2. Moving in an Unobserved Dimension7.3. Highway line mode7.4. Issues moving Observable Space7.5. Appealing Relationship8. Speed of Light Conjecture and E = mcc9. Inertia and a moving Unobserved Dimension9.1. Intrinsic Momentum and Resistance to Change9.2. Not Centrifugally generated9.3. Inertia Produced by Extra Dimensional Field9.4. Field Relationships Rule9.5. Flatland to Observable Space9.6. Greater than the Speed of Light9.7. Connection to Special Relativity9.8. Variations on Conjecture10. Interacting Spatial Fields and the movement of Photons10.1. Unconventional10.2. The interaction of Observed and Unobserved Space10.3. Why do photons move?10.4. Photons are like Sailboats10.5. Space has Structure10.6. Multidimensional Speed of Light11. Predictions of Model11.1. Image size11.2. Clock Variation11.3. Fusion in Stars12. Summary
6. Fundamental Issues Resolved6.1. “Mainstream model fix”6.2. Resolving Issues for the GEM from the First Paper7. Development of the Vu Model7.1. Caution, Unconventional7.2. Moving in an Unobserved Dimension7.3. Highway line mode7.4. Issues moving Observable Space7.5. Appealing Relationship8. Speed of Light Conjecture and E = mcc9. Inertia and a moving Unobserved Dimension9.1. Intrinsic Momentum and Resistance to Change9.2. Not Centrifugally generated9.3. Inertia Produced by Extra Dimensional Field9.4. Field Relationships Rule9.5. Flatland to Observable Space9.6. Greater than the Speed of Light9.7. Connection to Special Relativity9.8. Variations on Conjecture10. Interacting Spatial Fields and the movement of Photons10.1. Unconventional10.2. The interaction of Observed and Unobserved Space10.3. Why do photons move?10.4. Photons are like Sailboats10.5. Space has Structure10.6. Multidimensional Speed of Light11. Predictions of Model11.1. Image size11.2. Clock Variation11.3. Fusion in Stars12. Summary
1.2. Second of Four Papers
This is the second of four papers, which together describe the Multidimensional Geometric Expansion Model (GEM).The First paper, [2] hereon called the “First Paper”, established the basic relationships that define the geometric expansion of Observable Space. This, the second paper, has two sections. First, the effects of a specific variation in inertial mass are considered, and then a theoretical model is proposed that would produce the variation in inertial mass. The Third paper will focus on a more complete integration of the Vu model with the geometric expansion model described in the First Paper and Dark Matter. The Fourth paper will unify the relationships established for Observable and Unobservable space, to determine how well the model conforms to observation with respect to the location and rotation of Galaxies over Cosmological Time without Dark Energy.
1.3. Reason for Model – A Cosmological Red Shift and Dilation
The initial motivation for developing the proposed relationships and model was to generate a Cosmological Red Shift and Dilation Effects. The Multidimensional Geometric Expansion Model described in the First Paper yielded these effects but they would be not directly observed since the effects were counteracted by initial conditions.
1.4. Resolving “Mainstream” Ambiguities
One of the reaffirming aspects to the proposed inertial variation is that it resolves a number of fundamental Ambiguities that exist with the current “Mainstream” model. The “First Paper” described some of the issues pertaining to the Cosmological Red shift. For convenience, the fundamental ambiguities are briefly reiterated.1. Photons change but they should not.From Special Relativity it is established that the faster an object moves, the slower change can occur, and if an object were moving at the speed of light, nothing would change. This poses the question, how can a photon change its energy content and wavelength if it is moving at the speed of light? [7]2. Energy is Destroyed. The principal of Conservation of energy states that energy cannot be created or destroyed. Where did the energy from the cosmological photons go? The energy is no longer in the Observable Universe, there is no lingering heat dissipated into space. [8] 3. Matter and Energy are no longer equivalent over time, yet it is a predicted equivalency [1]. For example, the one gram of matter that drifted in an empty region of space would still be a gram of matter for all time, yet the one gram of radiant energy is diminishing over time. Existence Forever ProblemIt would seem that existence should come at some kind of energy cost. How could a small rock drifting somewhere in an empty cold region of space exist forever? Energy concentrations disperse over time. Shouldn’t the intrinsic rest energy of a mass somehow dissipate as well? If the energy of the photon is diminished over time, shouldn’t the energy of “rest mass” diminish over time? Wouldn’t a model that maintains the equivalence between matter and energy with the passage of time be preferred to a model that does not?
1.5. Heading, Figure, Equation Designations and Notation
HeadingsInitially the first number was to correspond to the paper designation. This would be the second paper, so all chapters in this paper would be demarcated with a 2. The publishers of the first paper removed these first number designations, (except in the Outline). It does make for a simpler looking text and avoids some confusion; people would wonder why the first chapter in this paper begins with a 2. EquationsThe purpose of the initial numbering system used by me was to simplify the cross reference to equations between papers. A Formula with a 1.3.4 designation would have been located in the first paper, third chapter and the fourth equation in that chapter. Now, since the numbering system has been changed by the publisher, formulas that are referenced from another paper will instead specifically denote what paper the formula was derived. For example, Paper 1, 2.3 would refer to a formula in the first paper, second chapter, third equation in that chapter. FiguresFigures are numerated by sequential location within the paper.Notation for RatiosThe same notational standard for equations established for the first paper will be used; newer measures are divided by older measures. For example, 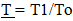 , is the “absolute ratio of time” where an earlier Absolute location in time is divided by the present Age of the Universe.Unobserved Space Expressions written in italicRelationships that are derived from the effects associated with Unobserved space and Vu will be written in italic. For example,
, is the “absolute ratio of time” where an earlier Absolute location in time is divided by the present Age of the Universe.Unobserved Space Expressions written in italicRelationships that are derived from the effects associated with Unobserved space and Vu will be written in italic. For example, 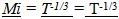 describes how Inertial Mass of an object proportionally changes over the Absolute ratio of time. The ratio of time is the same for both unobserved space and observed space, so it need not be expressed in iliac.
describes how Inertial Mass of an object proportionally changes over the Absolute ratio of time. The ratio of time is the same for both unobserved space and observed space, so it need not be expressed in iliac.
1.6. Similar Proposal by another Person
It has been particularly frustrating to find a reference or link to an internet web page that I recall looking at about 7 years ago (+ or – 2 years). The paper proposed that inertial mass could be lost over time, thereby producing a Cosmological Red Shift. Despite over 4 hours of searching I could not find the web site, nor could I find any published papers.This “lost paper” was published on the internet well before my Vu Model. I remember dismissing the paper since it was predicting contracting orbital relationships whereas the expansion of Observable Space, as described in the First Paper, was establishing expanding orbital relationships. I also remember being rather intrigued by the ideas. A “blue shifting” of present measures caused an observed “red shift”. It was when I developed the Vu model and its prediction that Inertial Mass would vary, thereby producing an Observable Cosmological Red shift, that I remembered the previous paper stating the same effect. I do not recall the author of this missing paper providing a model upon which to produce this variation in inertial Mass, nor do I recall any specific formulas. I would appreciate it if someone could help me find the author, or a copy of his work. I would include the information in the Third or Fourth Paper. To help identify the paper I remember the Author of the paper stating that he was a graduating physics student and his professor encouraged him to print it so that others can see the ideas.Also I’d like to send a “thank you” to the professor who encouraged his student, even if the ideas seemed outlandish.I was able to find another paper written by Robert S Fritzius and it proposes a cosmological red shift by the blueing of present spectra by an increase in the electromagnetic field but there is no correlation to a loss of mass. [9]
2. Spatial and Inertial Mass
The equivalency between inertial mass and gravitational or spatial mass has become a foundation upon which basic principles and relationships have been built. [10] Actually, this paper proposes that inertial and Spatial Mass are two independent properties of Mass and equivalency is only locally observed. Upon reflection, it is rather amazing to think that these two effects of mass should be equivalent over time since they are associated with dramatically different physical causes.
2.1. “Mainstream” Equivalency Assumed
The following quotes typify the present assumptions regarding the equivalency of inertial mass and Spatial Mass.“we [...] assume the complete physical equivalence of a gravitational field and a corresponding acceleration of the reference system.”— Einstein, 1907 [11]and (same article)…“A little reflection will show that the law of the quality of the inertial and gravitational mass is equivalent to the assertion that the acceleration imparted to a body by a gravitational field is independent of the nature of the body. For Newton's equation of motion in a gravitational field, written out in full, it is:(Inertial mass) x (Acceleration) = (Intensity of the gravitational field) x (Gravitational mass).It is only when there is numerical equality between the inertial and gravitational mass that the acceleration is independent of the nature of the body.”— Albert Einstein, [11]
2.2. Equivalency Challenged, not Relativity
Since Einstein based Relativity on this notion of the Equivalency of Spatial and Inertial Mass, some may construe that Relativity is being challenged. This is not exactly the case. Locally, the relationships of Relativity are still valid. It is only over Cosmological periods of time that Relativity fails to accurately define fundamental relationships, as evidenced by the ambiguities described earlier. As inertial mass is lost orbital relationships contract, thereby maintaining the balance between centrifugal (inertial) forces and gravitational forces.
2.3. Justification of Equivalency Based on Stability
It is should be noted that the argument for equivalency is based on observations that are locally observed, based on the observed balance between gravitational and inertial forces in orbital relationships. However, the justification of equivalency because of stability can be challenged if the changes occur over Cosmological intervals of time. Over an observational period of 100 years, the change would still be small in relation to the age of the Universe. Over Cosmological intervals the loss of equivalency is realized and clearly evident, as will be shown shortly.
2.4. Spatial Mass
Spatial Mass is a property that imposes and is defined by field based relationships in Spacetime. It is assumed to be a spatial-temporal characteristic of an object that is a scalar based constant with respect to the structure of Observable Space. Since spatial mass is constant over time within Observable Space it is expressed as…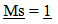 | (2.1) |
2.5. Inertial Mass
Inertial Mass is tied to a scalar number associated with an object that is modified by an independent function. This function is proposed to result in Inertial Mass to vary by…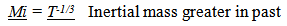 | (2.2) |
2.6. Building Blocks
If the object were an atom, the scalar number would be correlated to the Atomic Weight of the Atom. This scalar property of matter would be constant over time. It is as if Matter was composed of building blocks and the magnitude Spatial Mass is determined by the number of building blocks. The Inertial Mass of the object is determined by the number of building blocks, multiplied by another function. (This function will be correlated to a velocity along an extra dimension within an “Unobserved Space”).
3. Diminishing Inertial Mass 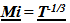
It will be shown that if the Inertial Mass of an Object varies by… then dynamic relationships that are defined by a balance between inertial an spatial forces change. Note the underline convention for ratios of past measures over present (or future). The italics are used to note that it is an expression based on a geometrically defined relationship with an “Unobserved Space”.
then dynamic relationships that are defined by a balance between inertial an spatial forces change. Note the underline convention for ratios of past measures over present (or future). The italics are used to note that it is an expression based on a geometrically defined relationship with an “Unobserved Space”.
3.1. Balancing Forces in Dynamic Systems and Collapsing Orbits
While spatial and inertial masses are proposed to be distinct and separate properties associated with objects, their properties are realized when forces are considered. An evaluation based on forces brings to light the variation in the two properties of matter.Most dynamic systems consist of a balance or interaction between inertial and spatial forces. What will be investigated now is the effect of diminishing the inertial forces of orbital systems, which typifies the balance between inertial and spatial forces.
3.2. The Relationships of Collapsing Orbits
First, assume that an orbiting system is dynamically balanced. Inertia forces equal spatial forces. As inertial force diminishes, the spatial force would draw in the orbiting body. As the orbiting body is drawn inwards, conservation of angular momentum would require the orbiting object to increase speed. This new speed would reestablish the necessary equilibrium or balance between centrifugal and inertial forces. As inertial mass is continuously lost, the orbiting body would continuously contract and the orbiting body would increase speed. Variation in Inertial ForceAs the inertial mass of the orbiting object decreases, the centrifugal force initially would diminish.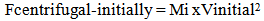 | (3.2) |
Where Vinitial equals the initial tangential velocity of the object. Since Mi varies by
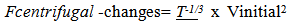 | (3.4) |
Conservation of Motion (Momentum)Conservation of Motion (Momentum) must be preserved, so as the orbiting objects are drawn together, the orbiting radius is diminished, and the orbiting velocity must increase in order to preserve conservation of Motion (momentum).For example consider a small ball on a string that is orbiting a finger. As the ball wraps the string on the finger, the speed increases, according to the principals of conservation of motion (momentum).The terms “Conservation of Motion” is used rather than Momentum since it is desired to remove the effect of the variation in the Mass of the orbiting objects to define the relationship. For example, consider a mass in motion, and based on the principal of conservation of momentum, the object will remain in motion unless some outside force is applied. Now if this mass were to eject mass in a direction orthogonal to its motion so it would not impart a force on the object, there would be no change in the velocity of the object. This is similar to the loss of inertial mass assumed (and predicted by the Vu Model). The velocity would not be affected by the change in the inertial mass of the object.Conservation of Rotational MotionFor orbing bodies, the conservation of Rotational motion becomes…Rotational intervals due to effects of Unobserved Space 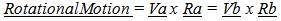 | (3.5) |
Where the subscripts a and b refer to two different conditions, such as before and after, and Va and Vb refers to the tangential velocity and Ra and Rb refers to the orbital radius.Balancing Orbital Relationships Orbital relationships are defined by a balance between inertial or centrifugal forces on one side of the balance, and spatially based forces defined by field effects on the other side. Incorporating the Conservation of Motion principal the orbital relationship becomes…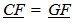 | (3.6) |
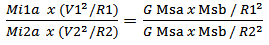 | (3.7) |
Mi1a = The measurable value for inertial mass “a” at historical location T1.Mi2a = The measurable value for inertial mass “a” at historical location T2Msa, Msb, gravitational masses a, b, maintain their measureG is the gravitational constantR, corresponds to the orbital radius, circular orbit assumedOrbital Velocity, and Radius over Cosmological TimeFrom conservation of rotational intervals we have…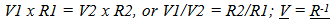 | (3.8) |
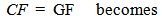 | (3.9) |
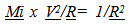 | (3.10) |
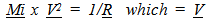 | (3.11) |
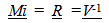 | (3.12) |
The inertial mass varies over time by the change in velocity of observable space along the unobserved dimension yields the variation in orbital radius and velocity over absolute time.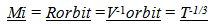 | (3.13) |
The orbital velocity and radial measures of orbiting systems change over time. The centrifugal acceleration variation over time by the orbiting mass, based on its velocity and radius becomes …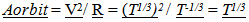 | (3,14) |
Special RelativityIt should be noted that the orbital relationships of electrons in atoms are mostly non relativistic in terms of the inertial mass of the electron.
3.3. Smaller Orbital Periods and Faster Clock Rates
The period of an orbit is described by the distance traveled divided by the time it takes to travel the distance.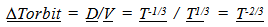 | (3.15) |
Any dynamic system that oscillates because of a balance between Spatial and Inertial Forces establishes a period or an interval of time. While the term “orbit” is used, any dynamic system is represented. 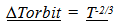 | (3.16) |
This means that when the Inertia Mass diminishes overtime, clock rates are speeding up. Clock rates observed in the past will appear to be slower.
3.4. Shrinking Rulers
If the orbital size of atoms shrinks due to the loss of inertial mass, then rulers, which are constructed with atoms, should also shrink. Since the radius of the atom was predicted to vary by… 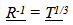 | (3.17) |
rulers composed of atoms should also vary at the same rate. 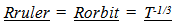 | (3.18) |
Objects observed in the past, would appear bigger using a smaller local ruler.
3.5. Radial Acceleration (Not Dark Matter)
The change in radial orbit due to the loss of inertial mass is of some interest to determine since it corresponds to an inward acceleration not expected in “Mainstream” models. As shown below it is a very small effect. 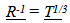 | (3.19) |
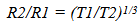 | (3.20) |
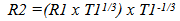 | (3.21) |
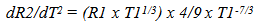 | (3.22) |
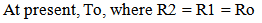 | (3.23) |
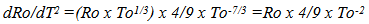 | (3.24) |
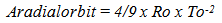 | (3.25) |
Effect Very Small – (Not Dark Matter)In a 10 x 109 year old universe, at a radius of 50,000 light years (a galaxy sized radius), the radial acceleration is about 4.7 x 10 -18 meters second-2. This is much smaller than the acceleration associated with Dark Matter, (about 10^8 times too small. Modified Newtonian Mechanics calculates the extra acceleration to be 10^-10 m/ss, [12]. The acceleration could also be determined by taking the velocity of the outer orbiting stars in a spiral galaxy, squaring it and dividing it by the radius and removing the accelerative effects associated with “real” mass. A more compete discussion of the Dark Matter issue will be made in the Fourth Paper.
4. Local and Cosmological Measures
4.1. Local Measures
Locally, these variations in measures of distance and time, using local inertial clocks and local rulers to measure local events would not be detectable. For example if the distance from the Earth to the Sun decreases to 1/2 over time, and the ruler used to measure the change similarly decreases to 1/2 its measure over time, proportionally all local measures stay the same. If temporal measures of an atomic clock, which uses dynamic resonance, is used to measure local intervals of time associated with some other orbital relationship, the speeding up of the intervals of time would not be observable.
4.2. Cosmological Measures
However, observations made of events in the distant past should show evidence of these effects. For example, From the Eye of God perspective, or from a local observer using a present ruler for comparison, a ruler in the past would be bigger than one used in the present since local rulers have contracted, so objects observed in the past should appear bigger than they do in the present by the variation in ruler size, after accounting for the observed reduction of image size do to distance.Similarly Clock rates in the past should appear to be slower. 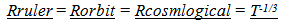 | (4.1) |
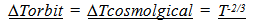 | (4.2) |
4.3. Dilation Effects Restored (Mostly)
Orbital temporal periods would now match the “stretch” of Observable Space, 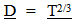 an effect that was not observable initially in the GEM. (The importance of matching
an effect that was not observable initially in the GEM. (The importance of matching 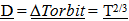 will be developed in more detail in the Third Paper when the cosmological location of galaxies over time are predicted.)Note, the change in observed size does not match the stretch of space since it varies by the 1/3 power, instead of the 2/3rds power. This topic will be discussed in more detail in the Third and Fourth paper.
will be developed in more detail in the Third Paper when the cosmological location of galaxies over time are predicted.)Note, the change in observed size does not match the stretch of space since it varies by the 1/3 power, instead of the 2/3rds power. This topic will be discussed in more detail in the Third and Fourth paper.
5. Cosmological Red Shift
The energy content of a photon produced by an electron “dropping” from one energy level to another is dependent upon the intensity of the electrostatic field the electron must drop through. The intensity varies to the inverse square of the distance to the nucleus. As an electron moves closer to the nucleus, due to the loss of inertial mass of the electron, the electrostatic field the electron orbits through becomes more intense. This increases the energy content associated with each of the orbital energy levels available to the electron within the atom. This more intense orbital field allows the creation or absorption of a higher energy photon when the electron falls or rises between orbital fields. A photon with more energy has a shorter wavelength, or it is “bluer”. Photons produced in the present are “bluer” than photons produced in the past.
5.1. Energy Variation over Cosmological Time
What will be done now is to determine the energy variation associated with the change in an electron’s orbit over time. This energy variation can then be used to establish the variation in the wavelength over time.Potential Energy of Spatial Field by orbital distance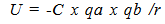 | (5.1) |
C represents Coulombs constant, qa and qb represent the value of charge, (“spatial like building blocks”), with r representing the distance from the center of orbit. Since C is constant, as well as the property of charge, the energy variation of the orbital relationship becomes…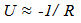 | (5.2) |
which, transforms to 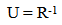 | (5.3) |
The radius of orbiting objects would vary by… so….
so…. 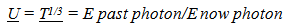 | (5.5) |
Notation CautionNote the expression is for the observed energy content of an old photon observed in the present.The further in the past a photon is produced, the less energy is imparted to the photon due to the less intense electrostatic field surrounding the electron orbital shells. (Ignoring for now the effects predicted from observable space described in the First Paper)
5.2. Cosmological Red Shift, λ measured
Translating 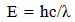 | (5.6) |
to a ratio of past over present measures for wavelength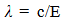 | (5.7) |
to yield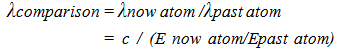 | (5.8) |
It is tempting to use the variation for the speed of light used for observable space derived in the First paper,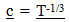 | (5.9) |
but the relationships developed in this Paper were based on the effects due to the loss of inertial mass, the variation in the speed of light was considered already for observable space, so instead of…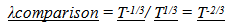 | (5.10) |
we have …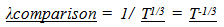 | (5.11) |
This relationship does not yet match the variation in the wavelength with the stretch of observable space described in the First Paper. (The “I” in 11.3 refers to an equation in the First Paper)The desirability for this “2/3”rds model to represent the expansion of Space will be discussed in much more detail in the fourth paper where the location of galaxies is predicted with respect to their historical or cosmological location in time and the observed Red shift. The following link from NASA shows that the result of a 2/3 rds model also corresponds to a measure of the age of the Universe if the expansion rate was determined by matter with no dark energy in a “flat universe” (Flat corresponds to a Euclidian based geometry where straight lines are straight. No curvature to space.) http://map.gsfc.nasa.gov/universe/uni_age.html [13]Plus Shrinking rulersHowever, this wavelength would be measured using a smaller ruler than what was used when the photon was created. Now the measured wavelength of light matches the stretch of observable space. This corresponds to the observed Cosmological Red Shift. (Another piece of the puzzle is fitting together).
(The “I” in 11.3 refers to an equation in the First Paper)The desirability for this “2/3”rds model to represent the expansion of Space will be discussed in much more detail in the fourth paper where the location of galaxies is predicted with respect to their historical or cosmological location in time and the observed Red shift. The following link from NASA shows that the result of a 2/3 rds model also corresponds to a measure of the age of the Universe if the expansion rate was determined by matter with no dark energy in a “flat universe” (Flat corresponds to a Euclidian based geometry where straight lines are straight. No curvature to space.) http://map.gsfc.nasa.gov/universe/uni_age.html [13]Plus Shrinking rulersHowever, this wavelength would be measured using a smaller ruler than what was used when the photon was created. Now the measured wavelength of light matches the stretch of observable space. This corresponds to the observed Cosmological Red Shift. (Another piece of the puzzle is fitting together).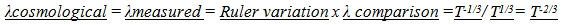 | (5.13) |
6. Fundamental Issues Resolved
The equivalency between Matter and radiant energy over time is now restored. This solution works for the GEM and somewhat for the “mainstream” model.
6.1. “Mainstream Model Fix”
If the measured Wavelength varies by, 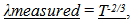 | (6.1) |
which matches the expected variation due to the stretch of space. The energy variation of the photon, after accounting for the change in in ruler size becomes…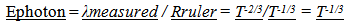 | (6.2) |
Which corresponds to the loss of inertial mass.The inertia of an object now diminishes at the same rate the energy of a photon must be changing.From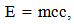 | (6.3) |
and the speed of light being a constant over time, 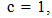 | (6.4) |
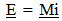 | (6.5) |
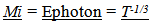 | (6.6) |
The energy content of a “rest mass” and a photon change their proportional value at the same rate and now maintain their equivalency over time. A gram of energy and a gram of matter are always observed to maintain their equivalence.Still “Mainstream” inconsistenciesThere are still inconsistencies with respect to general relativities prediction where the cosmological red shift correlates to the stretch of space due to the stretch of space, not also because of ruler variation.
6.2. Resolving Issues for the GEM from the First Paper
The proposed variation in inertial mass works perfectly for the GEM. Energy equivalency is restored, Dilation effects are established, and a Cosmological Red Shift is produced that match expectations. Energy IssueThe First Paper predicted that the energy content of a photon would vary by…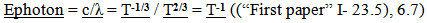 Yet the intrinsic energy content of a gram of matter in the first paper varied by
Yet the intrinsic energy content of a gram of matter in the first paper varied by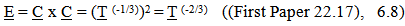 A gram of radiant energy did not equal a gram of matter over time. This issue is now resolved since the inertial mass also varies over time, effecting the energy content of Mass.
A gram of radiant energy did not equal a gram of matter over time. This issue is now resolved since the inertial mass also varies over time, effecting the energy content of Mass.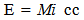 | (6.9) |
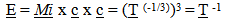 | (6.10) |
Matter loses its energy content at the same rate that radiant energy does, thereby preserving the equivalency between matter and energy. Another piece of the puzzle is fitting together.Conservation of EnergyAlso the conservation of energy principal is preserved locally within observable space over time. However, from the “Eye of God” perspective it can be seen that existence comes at a cost in energy, even for a rock drifting in a cold empty region in outer space.Special Relativity and ChangeThe issue as to how a photon changes its wavelength when it is moving at the speed of light with the requirement of special relativity that does not allow change to occur when objects are moving at the speed of light is also resolved. The variation in observed wavelength is a result of comparing the photon produced in the past with one produced in the present. The photon maintains its structural and proportional relationship relative to the fabric of Observable Space. The locally observed speed of light, wavelength and energy content is always fixed or invariant to a local observer. This invariance is preserved all during the time the photon travels through Observable Space. Dilation issueThe expansion of Observable Space described in the First Paper produced no temporal or spatial dilation effects. This was because clock rates and sizes were smaller in the past and the dilation of Space exactly countered the effect. Now this issue is mostly resolved. Time dilation corresponds to the inverse of the stretch of space = 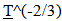 , while image size measures using ruler variation varies by
, while image size measures using ruler variation varies by 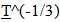 Cosmological Red Shift issueSimilar to the Dilation issue, there was no observable Cosmological red shift predicted in the First Paper. The increase in the wavelength due to the stretch of space was cancelled out by the shorter wavelength of the photon produced in the past. The model now predicts an observable cosmological redshift and it happens to also match the stretch of Space,
Cosmological Red Shift issueSimilar to the Dilation issue, there was no observable Cosmological red shift predicted in the First Paper. The increase in the wavelength due to the stretch of space was cancelled out by the shorter wavelength of the photon produced in the past. The model now predicts an observable cosmological redshift and it happens to also match the stretch of Space, 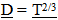 . The correlation to observation with respect to the location of galaxies will be discussed in more detail in the Fourth Paper.
. The correlation to observation with respect to the location of galaxies will be discussed in more detail in the Fourth Paper.
7. Development of the Vu Model
7.1. Caution, Unconventional
The preceding work was based on the idea that inertial mass is diminished over time. The relationships produced are interesting to consider on their own. The following work proposes a model upon which this variation is produced. It is unconventional, and as such, will lead to relationships that are derived by unconventional methods. For example, the relationship of E = mcc is derived using a simply expressed kinematic derivation. Those familiar with the derivation by Einstein will, most likely, be expecting a derivation using the same physical methodology as Einstein. This will not be the case. It is not the intention of this paper to define how relationships are changed by a change in inertial frames of reference as defined within our “observed space”. It is the intention of this paper to define how field based relationships establish certain physical effects using extra dimensional spatial relationships.It is hoped the reader will allow at least a speculative consideration of the model.
7.2. Moving in an Unobserved Dimension
While looking at some of the drawings used to describe the expansion of Observable Space it occurred to me that an alternative interpretation of the drawing could be useful. 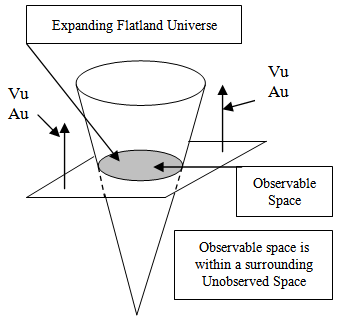 | Figure 2.1. Initially considered model example based on Flatland Universe example by transposing Historical Location with Velocity, Vu |
In the initial drawing, instead of the Vu vector now shown, there was the “arrow” of Historical Time and as time went on, the expansion of the Flatland Universe would be geometrically defined. Transposing the “arrow of time” for an unobserved velocity seemed obvious to consider since it looked like that. The Flatland Universe was moving in an Unobserved Dimension, or by analogy, our Observable Universe would be in motion along an unobserved Dimension. (The drawing also shows an unobserved deceleration Au; this will be discussed in the Third Paper).Imparting an Unobserved Velocity to Observable Space worked out well since the First Paper predicted that expansion comes at a kinematic cost, so Vu would have to diminish over time. If the wavelength was tied to the velocity along an unobserved dimension, than the wavelength would be greater when Vu was greater.
7.3. Highway Line Model
The wavelength of a photon was envisioned as an imparted property established as a result of a process that was somewhat like painting intermittent lines on a highway line. (One of the basic philosophical biases of these papers is that a physical foundation should be the basis for observed properties.) As the paint truck drives down the highway, a sprayer turns on and off to paint dashed lines that divide the highway and designate passing zones. If the truck drives faster, the dashed lines would be longer, assuming no other changes to the sprayer were made. By analogy, the faster the velocity along the unobserved dimension, the faster the Atom (Truck) would be moving, and the longer the wavelength would be as the electron dropped from one energy level to another. 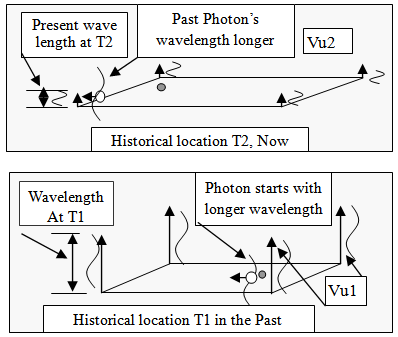 | Figure 2.2. Initially considered model for producing a Cosmological Red Shift |
This is illustrated in the following diagram. The lower picture is the wavelength imparted at T1, when Vu is faster. Once this wavelength is imparted, the wavelength would keep its relative measure established at its creation. Finally when observed in the present, it would measure to be longer than the wavelength generated today when Vu is smaller.
7.4. Issues with Moving Observable Space
There were a number of issues with this model as developed so far. Kind of troublesome was the variation of a Cosmological Red Shift that varied by T^1/3 which would not match the stretch of Observable Space which varied by D = T^(2/3) (Although it was kind of intriguing, or time consuming, to consider a different cosmological red shift relationship with the expected location of galaxies).Another issue was the requirement of imposing a motion of the entire Observable Universe along some unobserved dimension. This would require a lot of extra energy and adding complexity is not a good indication that the model is right.Also, as will be discussed in the Fourth Paper, the evolution and formation of galaxies becomes easier to explain if there is not the added requirement for all the galaxies to be in motion at the moment galaxies enter the Universe. (Actually it was this observation that first caused doubt of a moving Universe). The coup de grâce for moving the Observable Universe is explained in section 10 when momentum was combined with moving along an unobserved dimension.
8. Speed of Light Conjecture and E = mcc
If there is a Vu, how fast is it? Since the Vu is proposed to establish the wavelength property of light, it seemed reasonable that the speed of light should also be established by Vu. If our Observable Universe were in motion along an unobserved dimension with a velocity, Vu, which was equal to c√2, then the intrinsic energy of a rest mass becomes simply kenematically expressed.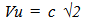 | (8.1) |
(Note, italics for relationship established from unobserved space)Then the Kinetic energy of an object would be… 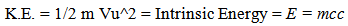 | (8.2) |
What Einstein called the “intrinsic” energy of a rest mass becomes kenematically based. This is an extremely simple derivation of E = m cc. [1]I so loved this simple derivation that it was difficult to abandon the explanation of a moving observable space and replace it with an Unobserved field space that was traveling through our observable space.
8.1. Photon Energy
Integrating the physical parameter of the wavelength of a photon to the speed of light, and then the frequency would seem to throw off the energy content of a photon. 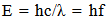 | (8.3) |
If the wavelength increased, then the energy content would seem to be diminished as well.Countering this effect, would be the prediction that the speed of light would be greater, as described in the First Paper, and by model description, the change in the speed of light would exactly offset the change in wavelength. The energy content of the photon would now always be the same. The frequency of the photon would similarly be preserved over time. The issues resolve when the predictions of the First paper are incorporated.
9. Inertia and a Moving Unobserved Dimension
The need to change the model to that of a multidimensional field passing through Observable space instead of the other way around became evident when the property of inertia was considered. This chapter describes why the change was required. Hopefully this historical struggle is not too distracting, it reflects some of the issues that had to be considered every time a change in relationships was proposed. The following figure illustrates a Flatland Universe in which three objects, A, B, and C are all experiencing the same Unobserved Velocity, Vu, at the same time. If all matter were moving along an unobserved dimension, then all matter would also have an unobserved property of momentum. 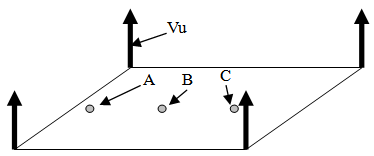 | Figure 2.3. Flatland Universe in relative motion with respect to a Spatial field orthogonal to Flatland |
9.1. Intrinsic Momentum and Resistance to Change
If the mass were in motion along an unobserved dimension, it would have properties of momentum but the observation of this momentum would not be directly seen in a Flatland Universe. Now if this mass were to change its location or move within observable space or the Flatland Universe, this would result in a change in direction of motion along the Unobserved Dimension. Any time an object changes its direction of motion, a resistance to that change in direction is experienced which would be perceived as the property of inertia and is illustrated in the following figure.As intuitive as this explanation initially appears, it is wrong. The shortcoming is described next. 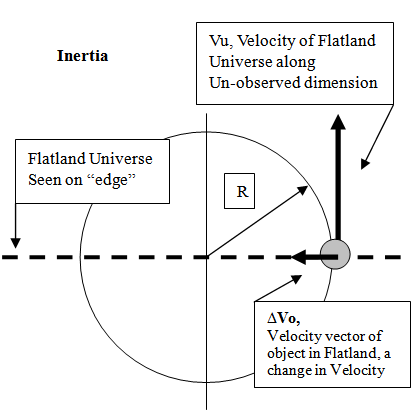 | Figure 2.4. Flatland Universe example of the centrifugal like process that generates inertia |
9.2. Not Centrifugally Generated
If matter was moving along an unobserved dimension, any change in motion in observable space would produce a variation in the momentum vector. Since this effect corresponds to a centrifugally like generated force, the physical realization of the inertial response for various changes in velocities of the object can be estimated given the following assumptions, which are consistent with the model. If Vu is large, and the change in velocity of the object is small, (negating the necessity for considering the effects of Special Relativity for now), then the following vector diagram illustrates the centrifugal acceleration generated based on the Flatland analogy.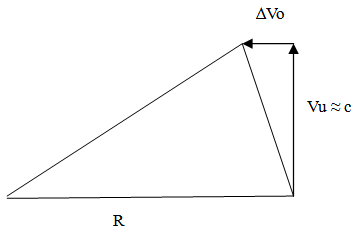 | Figure 2.5. Finding an error in the initial model with respect to the generation of inertial effects |
The ∆Vo corresponds to a change in Velocity within a Flatland Universe. This velocity change would always be perpendicular to Vu, thereby generating a Radius of Curvature to which the Object would move within Unobserved Space.If ∆Vo is small relative to Vu, the triangles 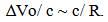 | (9.1) |
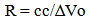 | (9.2) |
Solving for R and equating for a centrifugal acceleration from V2/R and determining how that acceleration that resists a change in velocity varies according to ∆Vo…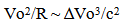 | (9.3) |
This would result in an acceleration resisting a change in direction that varies to the cube of the change in velocity of the object. This is clearly wrong since the inertial effect or the resistance to a change in velocity varies linearly with respect to the change in velocity for non-relativistic speeds.
9.3. Inertia Produced by Extra Dimensional Field
The solution was to transpose the relationship between a Flatland Universe in motion through an “unobserved Space to that of a Flatland Universe being “passed through” by a moving Unobserved Space. This allowed an inertial property to be assigned to mass without having the mass move. It is the magnitude of Vu that imparts the property of inertia and the intrinsic rest energy of a mass.
9.4. Flatland to Observable Space
Expanding the analogy of a Flatland Universe to our three spatial dimensions of Observable Space seems straight forward but requires a bit of imagination. An unobserved space that is moving orthogonally to our observed space will be illustrated in more detail in the Third and Fourth Papers.
9.5. Field Relationships Rule
It makes no difference locally with respect to the intrinsic rest energy of a mass if the mass were in actual motion, or it was a field effect passing through the mass causing the imparting of the energy content. A somewhat analogous example is the orthogonal movement of a magnetic field across a wire which produces the same current regardless if it is the motion of the field, or the wire.
9.6. Greater than the Speed of Light
The assertion that the motion observable space could be greater than the speed of light may seem to violate the principle regarding the impossibility for an object to move at a speed greater than the speed of light. It should be noted that this restriction is still preserved within observable space; in fact, this restriction is structurally tied to the motion along the unobserved dimension.
9.7. Connection to Special Relativity
Tying the inertial mass of an object to a dynamic process or a “generated property” seems to also be indicated by special relativity in that the faster an object moves in observable space, the greater the inertial mass becomes of the object. Also, by imposing an Unobserved Velocity that is tied to the speed of light, the speed of light is becoming a common denominator between the two theories.
9.8. Variations on Conjecture
It is possible to express slightly different versions of the speed of light Conjecture. The conjecture was based on the simple way the intrinsic rest energy of a mass becomes kenematically based. Other solutions can be possible. The “rest energy” of a mass may be only a proportion of the energy associated with an object as observed in our observable space with the rest of the “missing” energy residing in an “unobserved space”. For now, consider the following example. If the velocity along the unobserved dimensions were c, the intrinsic energy of a rest mass would be two times too big. However, if one half of this energy resided in “unobserved space” then the half we see in observed space would correspond to E = Mcc.
10. Interacting Spatial Fields and the Movement of Photons
10.1. Unconventional
This chapter presents an unconventional explanation regarding the movement of photons. As such, it is hoped the reader will evaluate the model based on the physical explanation, rather than its divergence from currently held beliefs.If the wavelength of a photon was determined by the velocity along an unobserved dimension, then it seemed necessary to consider a model by which the speed of light itself was also based on or established by the interaction between our Observable Space interacting with a moving Unobserved Space.
10.2. The Interaction of Observed and Unobserved Space
A key to unifying unobserved and observable space is tied to the physical properties of light. Light reveals the inter-dimensional interaction between observed and unobserved space. Uniting the two spaces in a dynamic inter-dimensional geometry results in a number of simple explanations for common physical phenomenon.
10.3. Why do Photons Move?
What makes the photon move so fast? Why does a photon move at all? One of the crowning achievements of Maxwell’s equations [14] was that once the electromagnetic and electric field relationships of the photon were incorporated into the physical properties of space, called the vacuum permittivity ε0, and vacuum permeability μ0, the speed of the photon could be predicted. But what establishes these two characteristics of Space? Is there a physical basis for establishing permeability and permittivity? Since the physical basis for the field relationships was based on dynamical response, couldn’t the action of photons also be a dynamical response based on field relationships?
10.4. Photons are Like Sailboats
It is proposed that the interaction of the photon with the moving and static multidimensional spacetime fields or structures of Space is what causes the photon to move. To visualize the extra dimensional relationships involved with the motion of photons, the flatland universe example is employed again. The following figure shows an expanding ring resulting from the intersection of a field relationship with the shape of a cone. (Another doubled use of a previous relationship.) If photons were “caught” by the expansion of the ring, the motion of the photons would be geometrically described. Photons would be like sailboats with the “keel” fixed in our Observable Space and the sail being pressed by Unobserved Space. It is the rate by which the “ring” expands which determines the speed of light. This interaction of two field relationships to the photon corresponds to the physical properties associated with the permittivity and permeability. (The First Paper illustrated the nature of dimensions, which correspond to measurable physical properties. These dimensions would correspond to or map to the structure of Space, both of Unobserved Space and Observable Space).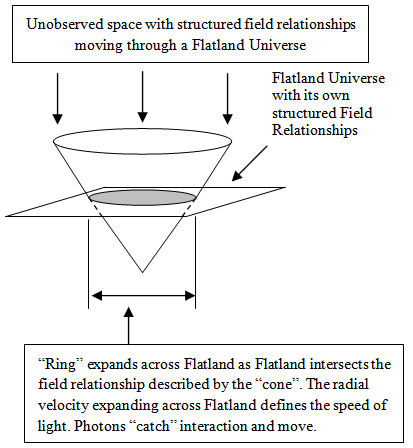 | Figure 2.6. Photons Caught between Fields Flatland “cone” example |
10.5. Space has Structure
The interaction or structure of the field of unobserved space is not point like as shown in the cone example, but is a local characteristic shared across Flatland. There is no actual cone. The cone represents possible paths at the moment the photon is created all across Flatland. Once a path is taken, the path would be a line on the possible paths illustrated by the cone. The photon is following the structural pattern of Unobserved and Observed Space. Space has a crystal like lattice structure.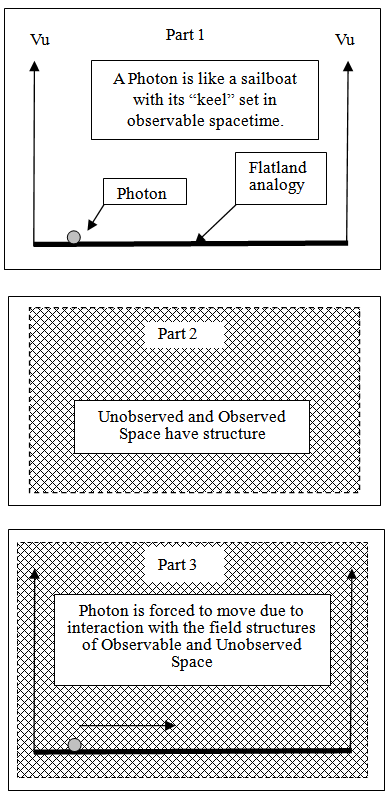 | Figure 2.7. Photons Following Structure |
10.6. Multidimensional Speed of Light
If light is traveling along Flatland at the speed of light, and it is also traveling along an unobserved dimension, then the multidimensional distance the light travels would be greater. This means that light also has a multidimensional speed. The following figure helps illustrate the relationship in a Flatland Universe. Plane ABCD is along an “unseen dimension” Plane EF, seen edge on, is perpendicular to plane ABCD. A relative observer is on the observed Plane EF. Plane ABCD is moving relative observer in Flatland at a velocity Vc. The relative Observer in Flatland “sees” light along the intersection of plane ABCD and the observers plane, seen on edge. 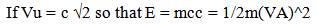 | (10.1) |
Then the “multidimensional” speed of light through Flatland and Unobserved Space is described by …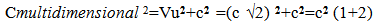 | (10.2) |
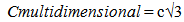 | (10.3) |
This multidimensional speed should be the same for our Observable Space, not just a Flatland since Flatland would just be a slice of the three spatial dimensions in our Observable Space. The speed of light in Observable Space would still be c.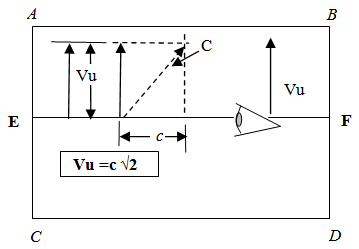 | Figure 2.8. Multidimensional Speed of Light |
11. Predictions of Model
Initially it would seem that there are a few possible cosmological observations that could verify the model.
11.1. Image Size
One variance from conventional “Mainstream” expectations and the GEM is the apparent size of galaxies. After accounting for the expected reduction of image size due to distance, there should be an additional size increase predicted by both the Vu model and the “Mainstream” model.The “Mainstream” model predicts the variation in observed image size would vary by the stretch of space (which closely maps to a 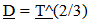 ). (This relationship to the stretch of space will be described in more detail in the Fourth Paper where cosmological models are compared.) The Vu model is predicting an image size variation by
). (This relationship to the stretch of space will be described in more detail in the Fourth Paper where cosmological models are compared.) The Vu model is predicting an image size variation by 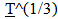 because of ruler variation.
because of ruler variation.
11.2. Clock Variation
Another predicted variation that could be potentially observable would be clock rates. A clock observed in the past should appear to be ticking slower in the past, compared to the faster clock rates of the present. This raises the question as to the possibility of observing this variation on a more local level. This issue will be discussed in more detail in the Fourth Paper after all the relationships have been developed.
11.3. Fusion in Stars
The prediction of higher intrinsic energy of matter in the past would result in the energy produced by fusion to be greater in the past. This increased energy output should be particularly evident from the collective light from the stars in galaxies, and supernovas. The further in the past these objects are observed the greater the energy output. The predicted change in luminously will be discussed in the Fourth Paper since the combined effects of Observable and Unobserved Space need to be considered.
12. Summary
If the inertial mass of matter diminished according to 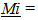
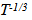 then a Cosmological Red shift is produced by the comparative “bluing” of spectra in the present compared to spectra produced in the past. This is due to the denser electrostatic field the orbital fields of electrons in the present compared to those in the past, along with using a smaller ruler in the present. Dilation effects are also produced based on a comparison of clock rates established by a balance between inertial and spatial forces. As a consequence of this loss of inertial mass, the energy content of photons traveling through the cosmos lose energy at the same rate that inertial mass lose intrinsic energy, thereby maintaining an equivalency between matter and radiant energy. This equivalency was lost in current “mainstream” models. Locally the wavelength and energy content of a photon maintains its local measure within the structure of Observable Space. The property of inertial mass is proposed to be an induced effect due to an extra dimensional field passing through the structure of Observable Space. The extra dimensional field and the field or structure of Observable Space are interconnected and share a common boundary described by the motion of photons. This interconnection of the two field spaces establishes the rate that the velocity associated with Unobserved Space diminishes with the passage of time.
then a Cosmological Red shift is produced by the comparative “bluing” of spectra in the present compared to spectra produced in the past. This is due to the denser electrostatic field the orbital fields of electrons in the present compared to those in the past, along with using a smaller ruler in the present. Dilation effects are also produced based on a comparison of clock rates established by a balance between inertial and spatial forces. As a consequence of this loss of inertial mass, the energy content of photons traveling through the cosmos lose energy at the same rate that inertial mass lose intrinsic energy, thereby maintaining an equivalency between matter and radiant energy. This equivalency was lost in current “mainstream” models. Locally the wavelength and energy content of a photon maintains its local measure within the structure of Observable Space. The property of inertial mass is proposed to be an induced effect due to an extra dimensional field passing through the structure of Observable Space. The extra dimensional field and the field or structure of Observable Space are interconnected and share a common boundary described by the motion of photons. This interconnection of the two field spaces establishes the rate that the velocity associated with Unobserved Space diminishes with the passage of time.Table 1. Relationships of Unobserved Space, The Vu Model
 |
| |
|
ACKNOWLEDGEMENTS
I forgot to acknowledge a couple of people in the First Paper and am thankful to have the opportunity to do so now.As a student in the School of Engineering at the University of Connecticut I was exposed to the Statics and Dynamics books written by Professor E. Russel Johnston Jr, and Professor Ferdinand Beer. These two books changed my life; principles were conformant to a geometry that were experienced as revelations. I was also fortunate to be a student of Professor Johnston in Graduate School at the University of Connecticut. I regret that I never told him how much I appreciated his books. Somehow the teacher student relationship poised a kind of boundary. If there is, as I am inclined to believe, a soul connection beyond the shell of life, then I pray my thank you is heard. If there is no connection, then those of us here know of my heartfelt appreciation of the guidance and understanding given to us by these men.
References
| [1] | Einstein, A. (1905), "Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig?", Annalen der Physik 18 (13):639–643,Bibcode:1905AnP...323..639E,doi:10.1002/andp.19053231314. See also the English translation. ″Does the inertia of a body depend upon its energy content?″ (1905). http://www.fourmilab.ch/etexts/einstein/E_mc2/www/. The title of this paper is out of respect to the wisdom of Einstein to propose what appears to be outrageous as a question. |
| [2] | Kulick, J, (2014) “A Multidimensional Geometric Expansion of Spacetime” International Journal of Theoretical and Mathematical Physics 2014, 4(2): 17-36DOI:10.5923/j.ijtmp.20140402.01 http://article.sapub.org/pdf/10.5923.j.ijtmp.20140402.01.pdf. |
| [3] | V Boys, 1894 “The Newtonian Constant of Gravitation” describes the Cavendish Experiment in the Weekly Evening Meeting, June 8, 1894, Royal Institution of Great Britain http://books.google.com/books?id=ZrloHemOmUEC&pg=PA355#v=onepage&q&f=false. |
| [4] | Eötvös, Loránd; “Mathematische and naturnissenschaftliche Berichte aus Ungarn” 8 65 (1889); Annalen der Physik (Leipzig) 68 11 (1922); Physical Review D 61(2) 022001 (1999). |
| [5] | Misner, Thorne, Wheeler, 1970 “Gravitation” pg 1081 Quoting response of Loránd Eötvös made in 1918 in Fejér and Mikola pg 259. |
| [6] | Einstein, 1916 Relativity: The Special and General Theories, English translation of 1916 book. http://en.wikisource.org/wiki/Relativity:_The_Special_and_General_Theory. |
| [7] | Ives, H. E.; Stilwell, G. R. (1938). "An experimental study of the rate of a moving clock". Journal of the Optical Society of America 28 (7): 215–226. doi:10.1364/JOSA.28.000215. |
| [8] | Brown, T.M. (1965). "Resource letter EEC-1 on the evolution of energy concepts from Galileo to Helmholtz". American Journal of Physics 33 (10): 759–765. Bibcode: 1965AmJPh..33..759B. doi:10.1119/1.1970980. |
| [9] | Fritzius R “Cosmological Redshift” (2010) A Shade Tree Online Publication, by Robert S. Fritziu http://www.datasync.com/~rsf1/cosmo_rs.htm. |
| [10] | Potter, Harold H.; "Some Experiments on the Proportionality of Mass and Weight", Proceedings of the Royal Society of London 104 588–610 (1923), doi:10.1098/rspa.1923.0130. |
| [11] | Einstein, Albert; "How I Constructed the Theory of Relativity", translated by Masahiro Morikawa from the text recorded in Japanese by Jun Ishiwara, Association of Asia Pacific Physical Societies (AAPPS) Bulletin, Vol. 15, No. 2, pp. 17-19 (April 2005). Einstein recalls events of 1907 in a talk in Japan on 14 December 1922. |
| [12] | M. Milgrom 2003 “Dark-matter Heretic”, interview of Physicist Mordehai Milgrom, American Scientist, January- February 2003, Volume 91, Number 1, Page 1. http://www. americanscientist.org/img/logo.gif. Also see notes in reference, May 2014 Wikipedia page, reference number 8. |
| [13] | Link to NASA site about Age of Universe and measure of Ho, Updated page December 2012.http://map.gsfc.nasa.gov/universe/uni_age.html. |
| [14] | C. Maxwell 1864, “A Dynamical Theory of Electromagnetic field”, pg 459, Philosophical Transactions of the Royal Society of London 155, 459-512 A_Dynamical_Theory_of_the_Electromagnetic_Field.pdf or http://en.wikisource.org/wiki/A_Dynamical_Theory_of_the_Electromagnetic_Field. |
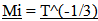 , with a corresponding loss of intrinsic energy, (The “_” notation represents a ratio of past measures over present measures so
, with a corresponding loss of intrinsic energy, (The “_” notation represents a ratio of past measures over present measures so 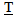 represents the ratio of the objects location in Cosmological Time divided by the Age of the Universe, and
represents the ratio of the objects location in Cosmological Time divided by the Age of the Universe, and 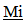 represents a ratio of the past over the present measures of inertial mass), then some interesting relationships result and a number of fundamental ambiguities in physics are resolved. Mentioning just one ambiguity; a gram of matter and a gram of radiant energy in intergalactic space now would maintain their equivalency over time, even though the photon loses energy as evidenced by the Cosmological Red Shift. As inertial mass is lost, relationships defined by a balance between inertial and spatial forces contract. (Spatial Forces are defined by spatial field based relationships associated with Gravity and Electromagnetism.) Spectra emitted or absorbed in the past would be “redder” than spectra produced in the present due to the denser atomic electrostatic field relationships in the present compared to the past. The contraction of atomic relationships also contracts local rulers which results in a measured Cosmological Red Shift that varies by
represents a ratio of the past over the present measures of inertial mass), then some interesting relationships result and a number of fundamental ambiguities in physics are resolved. Mentioning just one ambiguity; a gram of matter and a gram of radiant energy in intergalactic space now would maintain their equivalency over time, even though the photon loses energy as evidenced by the Cosmological Red Shift. As inertial mass is lost, relationships defined by a balance between inertial and spatial forces contract. (Spatial Forces are defined by spatial field based relationships associated with Gravity and Electromagnetism.) Spectra emitted or absorbed in the past would be “redder” than spectra produced in the present due to the denser atomic electrostatic field relationships in the present compared to the past. The contraction of atomic relationships also contracts local rulers which results in a measured Cosmological Red Shift that varies by 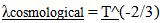 This establishes an alternative or additional explanation for the observed Recessional Red shift. Clock rates established by a balance between inertial and spatial forces speed up over time so intervals of time to vary by,
This establishes an alternative or additional explanation for the observed Recessional Red shift. Clock rates established by a balance between inertial and spatial forces speed up over time so intervals of time to vary by, 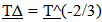 , which also produces an alternative or additional explanation for Time Dilation. The hypothetical geometrically defined model that could yield this variation in inertial mass is based on the following assumptions; 1. An extra dimensional space, (or Unobserved Space, or a set of extra dimensionally defined spatial field relationships), is in motion and is passing through our Observable Space. 2. It is the velocity of Unobserved Space through matter that imparts to mass the properties of inertia and “intrinsic” energy (E = mcc). 3. Unobserved Space and Observable Space are geometrically interconnected and are expanding at the same geometrically defined rate of
, which also produces an alternative or additional explanation for Time Dilation. The hypothetical geometrically defined model that could yield this variation in inertial mass is based on the following assumptions; 1. An extra dimensional space, (or Unobserved Space, or a set of extra dimensionally defined spatial field relationships), is in motion and is passing through our Observable Space. 2. It is the velocity of Unobserved Space through matter that imparts to mass the properties of inertia and “intrinsic” energy (E = mcc). 3. Unobserved Space and Observable Space are geometrically interconnected and are expanding at the same geometrically defined rate of 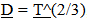 , where
, where 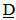 refers to the proportional distance between points on the spatial field. 4. The velocity of Unobserved Space, Vu, is diminished at a geometrically derived rate of
refers to the proportional distance between points on the spatial field. 4. The velocity of Unobserved Space, Vu, is diminished at a geometrically derived rate of 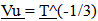 which results in the property of inertia to vary at the same rate. The model is called the “Vu model”. Analogously, just as we can visualize an expanding “flatland universe” in motion along an unobserved orthogonal dimension, we can visualize it instead as an Unobserved Space passing through a Flatland Universe. The same “rules” that were developed in a previous Paper, (A Multidimensional Geometric Expansion of Spacetime) [2] that established the geometric expansion of Observable Space also apply within Unobserved Space. This is the second of 4 papers that together define an alternative geometry for Spacetime and the Cosmos. The four papers together will establish a model that apparently will not need Dark Matter or Dark Energy to be consistent with the cosmological locations and rotational rates of Galaxies in the Universe.
which results in the property of inertia to vary at the same rate. The model is called the “Vu model”. Analogously, just as we can visualize an expanding “flatland universe” in motion along an unobserved orthogonal dimension, we can visualize it instead as an Unobserved Space passing through a Flatland Universe. The same “rules” that were developed in a previous Paper, (A Multidimensional Geometric Expansion of Spacetime) [2] that established the geometric expansion of Observable Space also apply within Unobserved Space. This is the second of 4 papers that together define an alternative geometry for Spacetime and the Cosmos. The four papers together will establish a model that apparently will not need Dark Matter or Dark Energy to be consistent with the cosmological locations and rotational rates of Galaxies in the Universe.
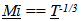 3.1. Balancing Forces in Dynamic Systems and Collapsing Orbits3.2. The Relationships of Collapsing Orbits 3.3. Smaller Orbital Periods and Faster Clock Rates 3.4. Shrinking rulers3.5. Radial acceleration (Not Dark Matter)4. Local and Cosmological measures4.1. Local Measures4.2. Cosmological measures 4.3. Dilation Effects Restored (Mostly)5. Cosmological Red Shift 5.1. Energy variation over cosmological time5.2. Cosmological red shift,
3.1. Balancing Forces in Dynamic Systems and Collapsing Orbits3.2. The Relationships of Collapsing Orbits 3.3. Smaller Orbital Periods and Faster Clock Rates 3.4. Shrinking rulers3.5. Radial acceleration (Not Dark Matter)4. Local and Cosmological measures4.1. Local Measures4.2. Cosmological measures 4.3. Dilation Effects Restored (Mostly)5. Cosmological Red Shift 5.1. Energy variation over cosmological time5.2. Cosmological red shift, 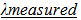 6. Fundamental Issues Resolved6.1. “Mainstream model fix”6.2. Resolving Issues for the GEM from the First Paper7. Development of the Vu Model7.1. Caution, Unconventional7.2. Moving in an Unobserved Dimension7.3. Highway line mode7.4. Issues moving Observable Space7.5. Appealing Relationship8. Speed of Light Conjecture and E = mcc9. Inertia and a moving Unobserved Dimension9.1. Intrinsic Momentum and Resistance to Change9.2. Not Centrifugally generated9.3. Inertia Produced by Extra Dimensional Field9.4. Field Relationships Rule9.5. Flatland to Observable Space9.6. Greater than the Speed of Light9.7. Connection to Special Relativity9.8. Variations on Conjecture10. Interacting Spatial Fields and the movement of Photons10.1. Unconventional10.2. The interaction of Observed and Unobserved Space10.3. Why do photons move?10.4. Photons are like Sailboats10.5. Space has Structure10.6. Multidimensional Speed of Light11. Predictions of Model11.1. Image size11.2. Clock Variation11.3. Fusion in Stars12. Summary
6. Fundamental Issues Resolved6.1. “Mainstream model fix”6.2. Resolving Issues for the GEM from the First Paper7. Development of the Vu Model7.1. Caution, Unconventional7.2. Moving in an Unobserved Dimension7.3. Highway line mode7.4. Issues moving Observable Space7.5. Appealing Relationship8. Speed of Light Conjecture and E = mcc9. Inertia and a moving Unobserved Dimension9.1. Intrinsic Momentum and Resistance to Change9.2. Not Centrifugally generated9.3. Inertia Produced by Extra Dimensional Field9.4. Field Relationships Rule9.5. Flatland to Observable Space9.6. Greater than the Speed of Light9.7. Connection to Special Relativity9.8. Variations on Conjecture10. Interacting Spatial Fields and the movement of Photons10.1. Unconventional10.2. The interaction of Observed and Unobserved Space10.3. Why do photons move?10.4. Photons are like Sailboats10.5. Space has Structure10.6. Multidimensional Speed of Light11. Predictions of Model11.1. Image size11.2. Clock Variation11.3. Fusion in Stars12. Summary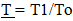 , is the “absolute ratio of time” where an earlier Absolute location in time is divided by the present Age of the Universe.Unobserved Space Expressions written in italicRelationships that are derived from the effects associated with Unobserved space and Vu will be written in italic. For example,
, is the “absolute ratio of time” where an earlier Absolute location in time is divided by the present Age of the Universe.Unobserved Space Expressions written in italicRelationships that are derived from the effects associated with Unobserved space and Vu will be written in italic. For example, 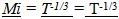 describes how Inertial Mass of an object proportionally changes over the Absolute ratio of time. The ratio of time is the same for both unobserved space and observed space, so it need not be expressed in iliac.
describes how Inertial Mass of an object proportionally changes over the Absolute ratio of time. The ratio of time is the same for both unobserved space and observed space, so it need not be expressed in iliac.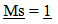
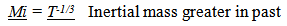
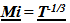
 then dynamic relationships that are defined by a balance between inertial an spatial forces change. Note the underline convention for ratios of past measures over present (or future). The italics are used to note that it is an expression based on a geometrically defined relationship with an “Unobserved Space”.
then dynamic relationships that are defined by a balance between inertial an spatial forces change. Note the underline convention for ratios of past measures over present (or future). The italics are used to note that it is an expression based on a geometrically defined relationship with an “Unobserved Space”. 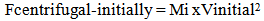

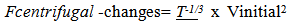
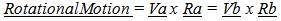
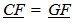
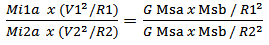
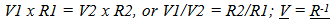
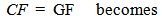
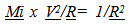
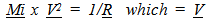
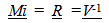
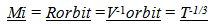
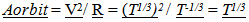
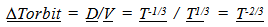
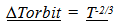
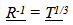
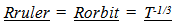
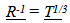
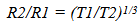
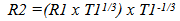
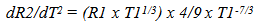
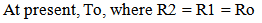
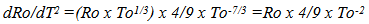
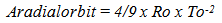
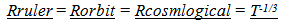
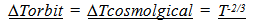
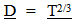 an effect that was not observable initially in the GEM. (The importance of matching
an effect that was not observable initially in the GEM. (The importance of matching 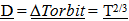 will be developed in more detail in the Third Paper when the cosmological location of galaxies over time are predicted.)Note, the change in observed size does not match the stretch of space since it varies by the 1/3 power, instead of the 2/3rds power. This topic will be discussed in more detail in the Third and Fourth paper.
will be developed in more detail in the Third Paper when the cosmological location of galaxies over time are predicted.)Note, the change in observed size does not match the stretch of space since it varies by the 1/3 power, instead of the 2/3rds power. This topic will be discussed in more detail in the Third and Fourth paper.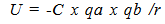
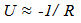
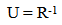
 so….
so…. 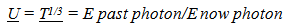
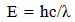
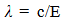
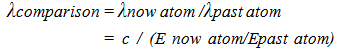
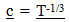
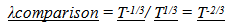
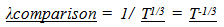
 (The “I” in 11.3 refers to an equation in the First Paper)The desirability for this “2/3”rds model to represent the expansion of Space will be discussed in much more detail in the fourth paper where the location of galaxies is predicted with respect to their historical or cosmological location in time and the observed Red shift. The following link from NASA shows that the result of a 2/3 rds model also corresponds to a measure of the age of the Universe if the expansion rate was determined by matter with no dark energy in a “flat universe” (Flat corresponds to a Euclidian based geometry where straight lines are straight. No curvature to space.) http://map.gsfc.nasa.gov/universe/uni_age.html [13]Plus Shrinking rulersHowever, this wavelength would be measured using a smaller ruler than what was used when the photon was created. Now the measured wavelength of light matches the stretch of observable space. This corresponds to the observed Cosmological Red Shift. (Another piece of the puzzle is fitting together).
(The “I” in 11.3 refers to an equation in the First Paper)The desirability for this “2/3”rds model to represent the expansion of Space will be discussed in much more detail in the fourth paper where the location of galaxies is predicted with respect to their historical or cosmological location in time and the observed Red shift. The following link from NASA shows that the result of a 2/3 rds model also corresponds to a measure of the age of the Universe if the expansion rate was determined by matter with no dark energy in a “flat universe” (Flat corresponds to a Euclidian based geometry where straight lines are straight. No curvature to space.) http://map.gsfc.nasa.gov/universe/uni_age.html [13]Plus Shrinking rulersHowever, this wavelength would be measured using a smaller ruler than what was used when the photon was created. Now the measured wavelength of light matches the stretch of observable space. This corresponds to the observed Cosmological Red Shift. (Another piece of the puzzle is fitting together).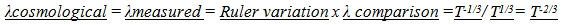
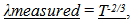
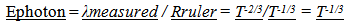
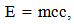
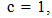
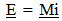
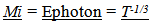
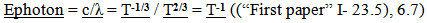 Yet the intrinsic energy content of a gram of matter in the first paper varied by
Yet the intrinsic energy content of a gram of matter in the first paper varied by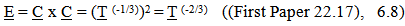 A gram of radiant energy did not equal a gram of matter over time. This issue is now resolved since the inertial mass also varies over time, effecting the energy content of Mass.
A gram of radiant energy did not equal a gram of matter over time. This issue is now resolved since the inertial mass also varies over time, effecting the energy content of Mass.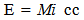
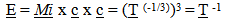
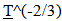 , while image size measures using ruler variation varies by
, while image size measures using ruler variation varies by 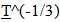 Cosmological Red Shift issueSimilar to the Dilation issue, there was no observable Cosmological red shift predicted in the First Paper. The increase in the wavelength due to the stretch of space was cancelled out by the shorter wavelength of the photon produced in the past. The model now predicts an observable cosmological redshift and it happens to also match the stretch of Space,
Cosmological Red Shift issueSimilar to the Dilation issue, there was no observable Cosmological red shift predicted in the First Paper. The increase in the wavelength due to the stretch of space was cancelled out by the shorter wavelength of the photon produced in the past. The model now predicts an observable cosmological redshift and it happens to also match the stretch of Space, 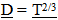 . The correlation to observation with respect to the location of galaxies will be discussed in more detail in the Fourth Paper.
. The correlation to observation with respect to the location of galaxies will be discussed in more detail in the Fourth Paper. 

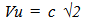
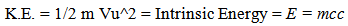
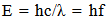



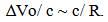
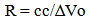
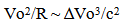


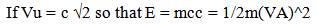
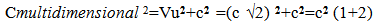
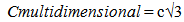

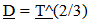 ). (This relationship to the stretch of space will be described in more detail in the Fourth Paper where cosmological models are compared.) The Vu model is predicting an image size variation by
). (This relationship to the stretch of space will be described in more detail in the Fourth Paper where cosmological models are compared.) The Vu model is predicting an image size variation by 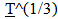 because of ruler variation.
because of ruler variation. 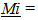
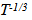 then a Cosmological Red shift is produced by the comparative “bluing” of spectra in the present compared to spectra produced in the past. This is due to the denser electrostatic field the orbital fields of electrons in the present compared to those in the past, along with using a smaller ruler in the present. Dilation effects are also produced based on a comparison of clock rates established by a balance between inertial and spatial forces. As a consequence of this loss of inertial mass, the energy content of photons traveling through the cosmos lose energy at the same rate that inertial mass lose intrinsic energy, thereby maintaining an equivalency between matter and radiant energy. This equivalency was lost in current “mainstream” models. Locally the wavelength and energy content of a photon maintains its local measure within the structure of Observable Space. The property of inertial mass is proposed to be an induced effect due to an extra dimensional field passing through the structure of Observable Space. The extra dimensional field and the field or structure of Observable Space are interconnected and share a common boundary described by the motion of photons. This interconnection of the two field spaces establishes the rate that the velocity associated with Unobserved Space diminishes with the passage of time.
then a Cosmological Red shift is produced by the comparative “bluing” of spectra in the present compared to spectra produced in the past. This is due to the denser electrostatic field the orbital fields of electrons in the present compared to those in the past, along with using a smaller ruler in the present. Dilation effects are also produced based on a comparison of clock rates established by a balance between inertial and spatial forces. As a consequence of this loss of inertial mass, the energy content of photons traveling through the cosmos lose energy at the same rate that inertial mass lose intrinsic energy, thereby maintaining an equivalency between matter and radiant energy. This equivalency was lost in current “mainstream” models. Locally the wavelength and energy content of a photon maintains its local measure within the structure of Observable Space. The property of inertial mass is proposed to be an induced effect due to an extra dimensional field passing through the structure of Observable Space. The extra dimensional field and the field or structure of Observable Space are interconnected and share a common boundary described by the motion of photons. This interconnection of the two field spaces establishes the rate that the velocity associated with Unobserved Space diminishes with the passage of time. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML