Mushfiq Ahmad1, K. Asraful Islam1, 2, M. Borhan Uddin1, 3
1Department of Physics, University of Rajshahi, Rajshahi, 6205, Bangladesh
2Department of Physics, Dhaka University of Engineering & Technology, Gazipur, Dhaka, 1700, Bangladesh
3Department of CSE, International Islamic University Chittagong, Chittagong, 4203, Bangladesh
Correspondence to: M. Borhan Uddin, Department of Physics, University of Rajshahi, Rajshahi, 6205, Bangladesh.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Classical oscillator differential equation is replaced by the corresponding (finite time) difference equation. The equation is, then, symmetrized so that it remains invariant under the change d→-d, where d is the smallest span of time. This symmetric equation has solutions, which come in reciprocally related pairs. One member of a pair agrees with the classical solution and the other is an oscillating solution and does not converge to a limit as d→0. This solution contributes to oscillator energy a term which is a multiple of half-integers.
Keywords:
Reciprocal Symmetry, Finite Difference Equation, Quantum Statistics, Classical Oscillator, Half-Integral Energy Levels
Cite this paper: Mushfiq Ahmad, K. Asraful Islam, M. Borhan Uddin, Reciprocal Symmetry and Classical Discrete Oscillator Incorporating Hall-Integral Energy Levels, International Journal of Theoretical and Mathematical Physics, Vol. 4 No. 3, 2014, pp. 110-113. doi: 10.5923/j.ijtmp.20140403.06.
1. Introduction
In 1900 Max Planck presented his quantum hypothesis [1], which sets a lower limit to energy transfer. In 1905 Albert Einstein presented his relativistic postulate [2], which sets an upper limit to velocity. Apart from the fact that, they talk of different quantities (energy and velocity), there is a reciprocal relation between the two. Every number has a unique reciprocal. [3], [4]. There will be no ambiguity if, instead of representing distance, time etc. by x, t, etc., we represent them by their reciprocals (x → 1/x, t → 1/t etc.). Here we can recall the principle of objectivity that physics should be independent of the quantities we define. The study of motion in terms of slowness (reciprocal of velocity) is as valid as the study in terms of velocity.Velocity is defined as the distance covered in unit time, V = x/t.Reciprocally, we may define slowness V’ as the reciprocal of V i.e. V’ = t/xPhysics does not depend on the quantities we define (objectivity). Therefore, it should be possible to describe motion in terms of slowness just as it is possible in terms of velocities [5].Let us consider the well known function exp(iwt) which describes an oscillating motion. Energy of the oscillator is proportional to the square of w. exp(iwt) is the solution of a differential equation. Classical oscillator differential equation can be replaced by the corresponding (finite time) difference equation. The equation, then, can be symmetrized so that it remains invariant under the change d→-d, where d is the smallest span of time. This symmetric equation has solutions, which come in reciprocally related pairs. The angular speed w is modified to w` or w``. w` contains a part with an integer. W`` contains a part with a half integer. This corresponds to quantum mechanical oscillator energy levels. f=a.exp(iwt) describes oscillation between -a and +a. if we make w=0, f describes free oscillation between –a and +a.The difference equation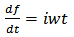 | (1.1) |
has a unique solution 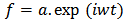 , f describe the motion of a harmonic oscillator if
, f describe the motion of a harmonic oscillator if 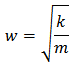 Where k is a constant and m is the mass.Classical energy of the oscillator
Where k is a constant and m is the mass.Classical energy of the oscillator 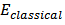 is proportional to
is proportional to 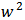
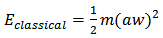 | (1.2) |
The corresponding finite difference equation has more solutions [6], which come in reciprocal pairs. When the function represents a harmonic oscillator, different solutions will contribute to oscillator energy in different ways. We intend to study these contributions and compare them to the corresponding quantum mechanical values.Let the oscillator having amplitude ‘a’ oscillate between –a and +a. We place two perfectly rigid reflecting walls at –a and +a. the presence of the walls does not influence the oscillation in any way. Now we make k=0 so that w=0. This makes the oscillator a free particle. Therefore, in the case (w=0) the non-vanishing energy term should the energy levels of a free particle bouncing between reflecting walls.
2. Oscillator Finite Difference Equation
Classical simple harmonic oscillator function f (with angular speed w) satisfies differential equation (1.1).To exploit its symmetry properties we replace the above differential equation by the corresponding symmetric finite difference equation [7]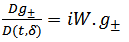 | (2.1) |
Where,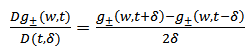 | (2.2) |
The above difference quotient has the following symmetry under the change δ→-δ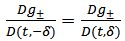 | (2.3) |
We require that at least one of the solutions, 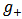 , of (2.1) should go over to (1.1) in the limit δ→0
, of (2.1) should go over to (1.1) in the limit δ→0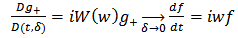 | (2.4) |
With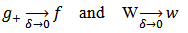 | (2.5) |
(2.1) has solutions in pairs. One of the pairs is [8]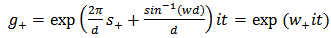 | (2.6) |
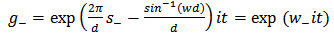 | (2.7) |
Where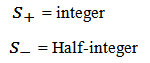 | (2.8) |
With the correspondence relation (for 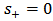 )
)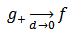 | (2.9) |
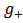 and
and 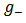 are related through the reciprocity relation
are related through the reciprocity relation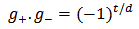 | (2.10) |
2.1. Assumption of Classical Physics
We consider an oscillator oscillating along x line between –a and +a 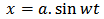 | (2.1.1) |
x=0 at t=0. we measure at intervals of d. we are not able to measure at any interval less than d. After time d the value of x is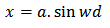 | (2.1.2) |
What is the value x after time d’, where d’<d? The classical assumption is 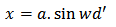 | (2.1.3) |
It is an assumption because no observations have been made for any interval d’<d. in (2.9) and (2.10) of this paper we have replaced assumption (2.1.3) by the less stringent assumptions below and we write for the displacement x 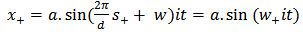 | (2.1.4) |
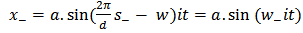 | (2.1.5) |
We require that 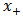 and
and  agree with the observed value at t=d so that
agree with the observed value at t=d so that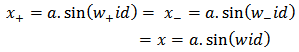 | (2.1.6) |
(2.1.4) and (2.1.5), therefore, express our ignorance about the values of x for t<d.
2.2. Classical and Quantum Energy Levels
The energies of the reciprocal symmetric oscillator 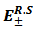 are [9]
are [9]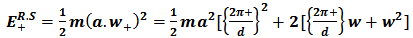 | (2.2.1) |
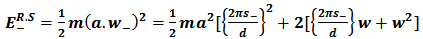 | (2.2.2) |
For s+ =0, (2.2.1) gives the classical value (1.3).The middle term of (2.2.2) is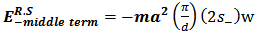 | (2.2.3) |
It corresponds to quantum mechanical value. [10]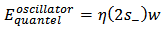 | (2.2.4) |
The important difference is that there is no Planck’s constant in (2.2.3).
3. Reciprocal Symmetry
Let 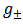 be of the form
be of the form 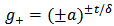 so that
so that 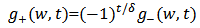 | (3.1) |
Consider equation (2.1)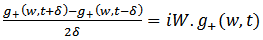 | (3.2) |
Using (3.1) we find that 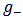 also satisfies the equation. This establishes reciprocal symmetry of (2.1), that the equation remains invariant under transformation (3.1).
also satisfies the equation. This establishes reciprocal symmetry of (2.1), that the equation remains invariant under transformation (3.1).
3.1. Reciprocal Symmetric Solutions
(2.1) has a pair of solutions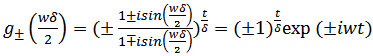 | (3.1.1) |
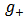 and
and 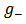 satisfy (2.1) with
satisfy (2.1) with 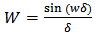 | (3.1.2) |
We may write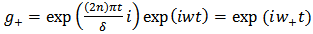 | (3.1.3) |
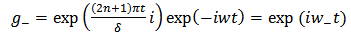 | (3.1.4) |
Where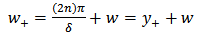 | (3.1.5) |
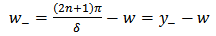 | (3.1.6) |
4. Classical and Hall-Integral Energy Levels
Simple harmonic oscillator function f satisfies the differential equation 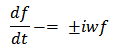 The corresponding finite difference symmetric equation is
The corresponding finite difference symmetric equation is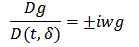 It has two solutions
It has two solutions 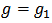 and
and 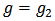 [10]
[10]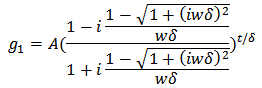 And
And 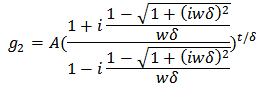 In the limit as
In the limit as 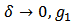 gives the classical oscillator function f
gives the classical oscillator function f 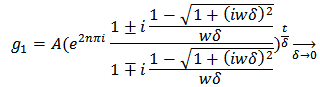
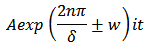 Half integral energy levels
Half integral energy levels  gives
gives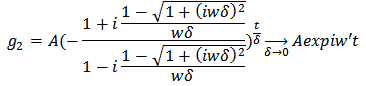 Where
Where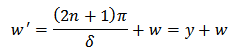 The energy of the oscillator is proportional to
The energy of the oscillator is proportional to 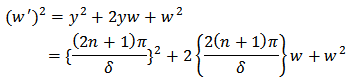 The middle terms contain half-integral multiples. To this extent it corresponds to quantum mechanical value.The first term of this equation,
The middle terms contain half-integral multiples. To this extent it corresponds to quantum mechanical value.The first term of this equation, 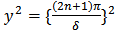 , corresponds to the energy levels of a free particle oscillating between reflecting walls. A similar term with (2n+1) replaced by 2n comes from
, corresponds to the energy levels of a free particle oscillating between reflecting walls. A similar term with (2n+1) replaced by 2n comes from 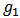 solution. Adding terms, we get the total energy, Ey, of a free particle oscillating between reflecting walls as
solution. Adding terms, we get the total energy, Ey, of a free particle oscillating between reflecting walls as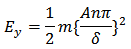 Where m is the mass, 2A is the width of the well and n is an integer.The energy of the oscillator is proportional to
Where m is the mass, 2A is the width of the well and n is an integer.The energy of the oscillator is proportional to 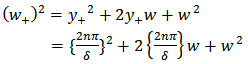 | (4.1) |
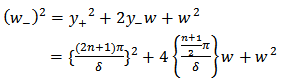 | (4.2) |
For n=0 (4.1) gives the classical value. The middle term of (4.2) is a product term of half-integers and w. to this extent it corresponds to quantum mechanical value.
5. Conclusions
The pair of reciprocal symmetric functions 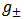 of (2.9) and (2.10) describes a classical oscillator, which has discrete energy levels (2.2.1) and (2.2.2). one of the terms (2.2.3) compares well with the corresponding quantum mechanical term (2.2.2).We have replaced oscillator differential equation by the corresponding symmetric discrete equation (2.1). This has brought to surface important parts of oscillator function, which were lost in the conventional solution. These parts contain discrete-integral and half-integral energy levels.
of (2.9) and (2.10) describes a classical oscillator, which has discrete energy levels (2.2.1) and (2.2.2). one of the terms (2.2.3) compares well with the corresponding quantum mechanical term (2.2.2).We have replaced oscillator differential equation by the corresponding symmetric discrete equation (2.1). This has brought to surface important parts of oscillator function, which were lost in the conventional solution. These parts contain discrete-integral and half-integral energy levels.
ACKNOWLEDGEMENTS
We are deeply indebted to Prof. Mushfiq Ahmad for his unwavering patience and thoughtful guidance to this research. His strong spirit of solving and meeting the challenging problems throughout the study have played very important role behind these achievements. We are very pleased for his moral affectionate behavior to the students.We wish to express our gratitude to the authority of Rajshahi University, Rajshahi, Bangladesh for helping us to this research.
References
| [1] | Max Planck, Annalen der Physik 4 (1901): 553. |
| [2] | On the Electrodynamics of moving bodies, Annalen der Physik, 17, 1905. |
| [3] | Mushfiq Ahmad, Homogeneous number system and reciprocal symmetric algebra.http://ajase.weebly.com/current-issue.html. |
| [4] | Mushfiq Ahmad, Derivation of relativistic law of addition of velocities from superposition of eigenfunctions and discreteness. http://arxiv.org/abs/0708.2593. |
| [5] | Mushfiq Ahmad. Discrete and Continuous Representat ion of the Same Motion. Physics Essays. March 2009; Vol. 22, No. 1. |
| [6] | Mushfiq Ahmad, Reciprocal Symmetry and Equivalence between Relativistic and Quantum Mechanical Concepts. (and references therein)http://www.arxiv.org/abs/math-ph/0611024. |
| [7] | Mushfiq Ahmad, Reciprocal Symmetry and Origin of Quantum Statistics. (and references therein) http://www.arXiv.org/abs/physics/0703194. |
| [8] | Mushfiq Ahmad, Reciprocal Symmetry and Origin of Quantum Statistics.http://www.arXiv.org/abs/physics/0703194. |
| [9] | Mushfiq Ahmad, Muhammad O.G.. Talukder, Reciprocal symmetry and unified classic-quantum oscillator and consistency between a particle in a potential well and a harmonic oscillator.http://arxiv.org/ftp/arxiv/papers/0705/0705.0730.pdf. |
| [10] | Robert H. Dicke and James P. Wittke. Introduction to Quantum Mechanics, Addison-Wesley Pub. Co., Inc. |

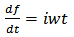
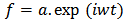 , f describe the motion of a harmonic oscillator if
, f describe the motion of a harmonic oscillator if 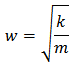 Where k is a constant and m is the mass.Classical energy of the oscillator
Where k is a constant and m is the mass.Classical energy of the oscillator 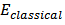 is proportional to
is proportional to 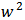
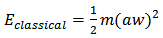
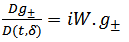
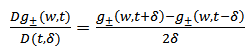
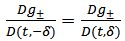
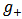 , of (2.1) should go over to (1.1) in the limit δ→0
, of (2.1) should go over to (1.1) in the limit δ→0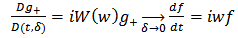
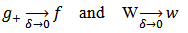
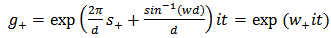
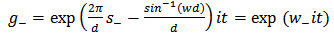
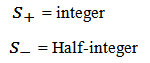
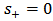 )
)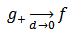
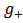 and
and 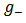 are related through the reciprocity relation
are related through the reciprocity relation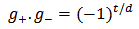
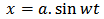
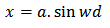
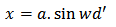
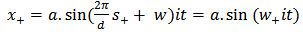
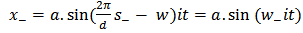
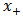 and
and  agree with the observed value at t=d so that
agree with the observed value at t=d so that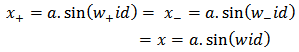
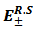 are [9]
are [9]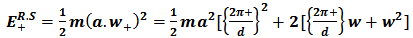
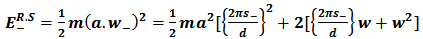
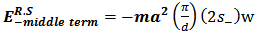
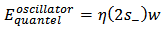
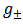 be of the form
be of the form 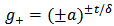 so that
so that 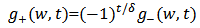
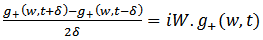
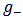 also satisfies the equation. This establishes reciprocal symmetry of (2.1), that the equation remains invariant under transformation (3.1).
also satisfies the equation. This establishes reciprocal symmetry of (2.1), that the equation remains invariant under transformation (3.1).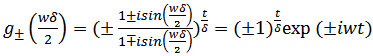
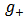 and
and 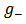 satisfy (2.1) with
satisfy (2.1) with 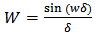
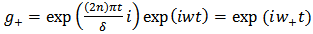
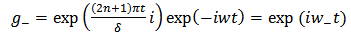
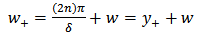
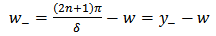
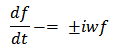 The corresponding finite difference symmetric equation is
The corresponding finite difference symmetric equation is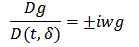 It has two solutions
It has two solutions 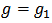 and
and 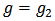 [10]
[10]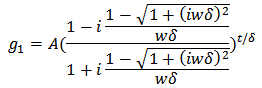 And
And 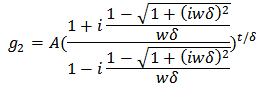 In the limit as
In the limit as 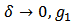 gives the classical oscillator function f
gives the classical oscillator function f 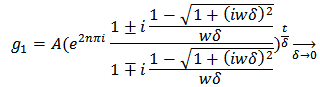
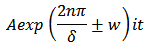 Half integral energy levels
Half integral energy levels 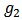 gives
gives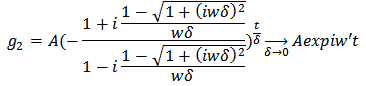 Where
Where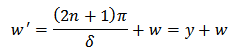 The energy of the oscillator is proportional to
The energy of the oscillator is proportional to 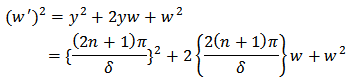 The middle terms contain half-integral multiples. To this extent it corresponds to quantum mechanical value.The first term of this equation,
The middle terms contain half-integral multiples. To this extent it corresponds to quantum mechanical value.The first term of this equation, 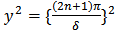 , corresponds to the energy levels of a free particle oscillating between reflecting walls. A similar term with (2n+1) replaced by 2n comes from
, corresponds to the energy levels of a free particle oscillating between reflecting walls. A similar term with (2n+1) replaced by 2n comes from 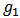 solution. Adding terms, we get the total energy, Ey, of a free particle oscillating between reflecting walls as
solution. Adding terms, we get the total energy, Ey, of a free particle oscillating between reflecting walls as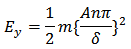 Where m is the mass, 2A is the width of the well and n is an integer.The energy of the oscillator is proportional to
Where m is the mass, 2A is the width of the well and n is an integer.The energy of the oscillator is proportional to 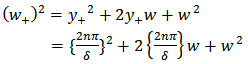
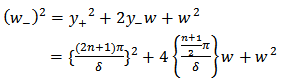
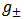 of (2.9) and (2.10) describes a classical oscillator, which has discrete energy levels (2.2.1) and (2.2.2). one of the terms (2.2.3) compares well with the corresponding quantum mechanical term (2.2.2).We have replaced oscillator differential equation by the corresponding symmetric discrete equation (2.1). This has brought to surface important parts of oscillator function, which were lost in the conventional solution. These parts contain discrete-integral and half-integral energy levels.
of (2.9) and (2.10) describes a classical oscillator, which has discrete energy levels (2.2.1) and (2.2.2). one of the terms (2.2.3) compares well with the corresponding quantum mechanical term (2.2.2).We have replaced oscillator differential equation by the corresponding symmetric discrete equation (2.1). This has brought to surface important parts of oscillator function, which were lost in the conventional solution. These parts contain discrete-integral and half-integral energy levels. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML