Omamoke O. E. Enaroseha1, E. G. Akpojotor2, Lawrence Atuma3
1Nigeria Atomic Energy Commission, Abuja and Nigeria Center for Nuclear Energy Studies, Port – Harcourt, Nigeria
2Physics Department, Delta State University, Abraka, Nigeria
3Physics Department, Delta State Polytechnic, Oghara, Nigeria
Correspondence to: E. G. Akpojotor, Physics Department, Delta State University, Abraka, Nigeria.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Anderson model is an important model in the theory of strongly correlated electron system. In this study, we explore the ground state of this model and the concept of electron correlation by bipartite lattice and prove rigorously theorems leading to the presence of spin singlet in the model. By using the results of Ueda et al [15] and Tian [16], we show theoretically that the ground state of the symmetric periodic Anderson model has a short – range order antiferromagnetism.
Keywords:
Periodic Anderson model, Antiferromagnetism, Strongly correlated system
Cite this paper: Omamoke O. E. Enaroseha, E. G. Akpojotor, Lawrence Atuma, Theorems to Demonstrate the Presence of Antiferromagnetism in the Periodic Anderson Model, International Journal of Theoretical and Mathematical Physics, Vol. 4 No. 3, 2014, pp. 96-102. doi: 10.5923/j.ijtmp.20140403.04.
1. Introduction
The role of physical models in investigating complicated systems is one of the most significant strategies in Theoretical Condensed Matter Physics. The point is that if the model is able to account for some of the well known properties of the system, then it is expected to account for the more complex properties. Now when one is interested in fundamental properties of the model, exploring the ground-state energy is a feasible starting point [1]. For example, one of us has shown that for any finite value of the physically realistic on-site Coulombic interaction, the ground state of the Hubbard model which is the simplest model for studying strongly correlated systems, is a spin singlet [2]. Thus to use the model to study complicated strongly correlated phenomena like superconductivity and ferromagnetism which require transition from the antiferromagnetic ordering to partial or full spin ordering, other interaction terms needs to be added [3-4]. This is the line of thinking that led to the formation of the Periodic Anderson Model (PAM) [5-7] often used to investigate the heavy fermion systems which are well-known strongly correlated electron systems that exhibit unusual thermodynamic, magnetic, and transport properties [8]. Take a finite lattice 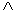 with
with 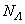 lattice points. Neglecting the orbital degeneracy for the localized electrons, the Hamiltonian of the PAM can be written in the form [9]
lattice points. Neglecting the orbital degeneracy for the localized electrons, the Hamiltonian of the PAM can be written in the form [9]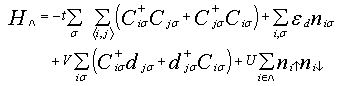 | (1) |
where 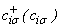 is the creation (annihilation) of electrons, which creates (annihilates) an itinerant electron of spin σ at site i. Similarly,
is the creation (annihilation) of electrons, which creates (annihilates) an itinerant electron of spin σ at site i. Similarly, 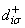 and
and 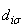 are the fermion operators for the localized electrons.
are the fermion operators for the localized electrons. 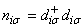 and
and 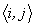 denotes a pair of lattice sites,
denotes a pair of lattice sites, 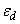 is a local potential, V is the hybridization matrix element and U > 0 represent the on-site Coulomb interaction for the localized electrons.Since its introduction, the PAM and its variants constitute an important research topic in theoretical condensed matter physics, particularly in the context of strongly correlated electron system. Most of the many body techniques commonly used in condensed matter physics can be learnt in this context. Also there are some theoretical tools and concepts which apply to this model only [10-13]. The aim of this paper is to prove that the ground state of the symmetric PAM is a spin singlet.
is a local potential, V is the hybridization matrix element and U > 0 represent the on-site Coulomb interaction for the localized electrons.Since its introduction, the PAM and its variants constitute an important research topic in theoretical condensed matter physics, particularly in the context of strongly correlated electron system. Most of the many body techniques commonly used in condensed matter physics can be learnt in this context. Also there are some theoretical tools and concepts which apply to this model only [10-13]. The aim of this paper is to prove that the ground state of the symmetric PAM is a spin singlet.
2. Methodology and Mathematical Formulation
Lattice 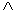 is called bipartite with respect to the Hamiltonian
is called bipartite with respect to the Hamiltonian 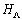 if it can be divided into two sublattices A and B, such that hopping of electrons does not occur between sites in the same sublattices. For a bipartite lattice, the signs of parameters t and V are not important for the mathematical analysis of this Hamiltonian. They can be changed by a unitary transformation. For definiteness, we shall choose t > 0 and V > 0 in the following.To begin with, we first write the Hamiltonian
if it can be divided into two sublattices A and B, such that hopping of electrons does not occur between sites in the same sublattices. For a bipartite lattice, the signs of parameters t and V are not important for the mathematical analysis of this Hamiltonian. They can be changed by a unitary transformation. For definiteness, we shall choose t > 0 and V > 0 in the following.To begin with, we first write the Hamiltonian 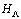 of the symmetric PAM in a generalized Hubbard Hamiltonian. For simplicity, let us consider a specific bipartite lattice: the two-dimensional square lattice
of the symmetric PAM in a generalized Hubbard Hamiltonian. For simplicity, let us consider a specific bipartite lattice: the two-dimensional square lattice 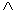 with N = L2 lattice points (the lattice constant is taken to be unity). Take two identical copies of this square lattice,
with N = L2 lattice points (the lattice constant is taken to be unity). Take two identical copies of this square lattice, 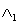 and
and 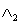 . We make a doubly layered lattice
. We make a doubly layered lattice 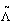 by connecting the corresponding lattice points of
by connecting the corresponding lattice points of 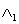 and
and 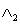 with bonds of length 1. Now, each point of
with bonds of length 1. Now, each point of 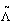 is labelled by r = ( i, m) where m = 1 or 2. Obviously,
is labelled by r = ( i, m) where m = 1 or 2. Obviously, 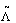 has
has 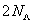 lattice points. Next, we introduce new fermion operators fra by
lattice points. Next, we introduce new fermion operators fra by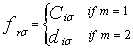 | (2) |
If we assume in Eq. (1) that, when 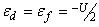 , the Hamiltonian of the PAM is called Symmetric. With the definitions of
, the Hamiltonian of the PAM is called Symmetric. With the definitions of 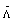 and fra, the Hamiltonian
and fra, the Hamiltonian 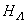 of the symmetric PAM can be rewritten as the Hamiltonian of a generalized Hubbard model on
of the symmetric PAM can be rewritten as the Hamiltonian of a generalized Hubbard model on 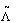 by ignoring an uninteresting constant
by ignoring an uninteresting constant 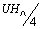 .
.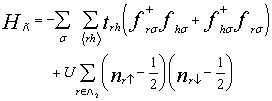 | (3) |
where the new hopping constants trh are defined by | (4) |
It is easy to see 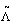 is still bipartite with respect to
is still bipartite with respect to 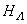 . Furthermore, we observe that the electrons in the second layer (the d–electron layer) do not hop and have an on-site Coulomb repulsion, while the electrons in the first layer are itinerant without interaction. To account for this interaction, we introduce an auxiliary interaction operator
. Furthermore, we observe that the electrons in the second layer (the d–electron layer) do not hop and have an on-site Coulomb repulsion, while the electrons in the first layer are itinerant without interaction. To account for this interaction, we introduce an auxiliary interaction operator 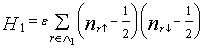 | (5) |
to the Hamiltonian 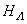 and study the ground state of the new Hamiltonian
and study the ground state of the new Hamiltonian 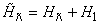 . The
. The 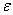 in Equation (5) is a generalized interacting potential so that the interaction can be switched off by letting
in Equation (5) is a generalized interacting potential so that the interaction can be switched off by letting 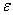 → 0. It is pertinent to point out that this interaction operator in Equation (5) will make it straightforward in future to generalized the proofs here so that by choosing the appropriate interacting elements, we can obtain a generalized Anderson model from which we can in turn also obtain the single site impurity Anderson model and the Kondo model depending on the material system we wish to study. The purposes of the proofs are to show the existence of a short-range antiferromagnetic d-electron spin correlation in the ground state
→ 0. It is pertinent to point out that this interaction operator in Equation (5) will make it straightforward in future to generalized the proofs here so that by choosing the appropriate interacting elements, we can obtain a generalized Anderson model from which we can in turn also obtain the single site impurity Anderson model and the Kondo model depending on the material system we wish to study. The purposes of the proofs are to show the existence of a short-range antiferromagnetic d-electron spin correlation in the ground state 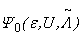 of the positive-(
of the positive-(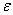 , U) symmetric PAM at half filling. However, reflection positivity in the spin space does not hold in this case. Fortunately, by the well-known unitary particle-hole transformation
, U) symmetric PAM at half filling. However, reflection positivity in the spin space does not hold in this case. Fortunately, by the well-known unitary particle-hole transformation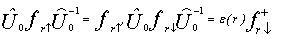 | (6) |
where 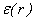 = 1 if r ∈ A and
= 1 if r ∈ A and 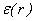 = -1 if r ∈ B, the Hamiltonian is of the same form, which has reflection positivity in the spin space. Obviously, the transformed Hamiltonian has the same spectrum. In the following, we shall first study the ground state
= -1 if r ∈ B, the Hamiltonian is of the same form, which has reflection positivity in the spin space. Obviously, the transformed Hamiltonian has the same spectrum. In the following, we shall first study the ground state 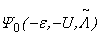 of the Hamiltonian
of the Hamiltonian 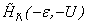 at half filling and then transform it back to the corresponding ground state
at half filling and then transform it back to the corresponding ground state 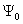 (
(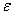 ,
,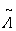 ) of
) of 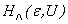 by the inverse of the particle-hole transformation.We observe that
by the inverse of the particle-hole transformation.We observe that 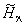 commutes with
commutes with 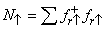 and
and 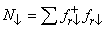 respectively. Consequently, the Hilbert space of
respectively. Consequently, the Hilbert space of 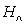 can be divided into numerous subspaces. Each of them is characterized by a pair of integers (N = n1, N= n2). For this Hamiltonian, following the formalism of Ref [14], we proved the following theorem.Theorem. For any given even integer N, the ground state
can be divided into numerous subspaces. Each of them is characterized by a pair of integers (N = n1, N= n2). For this Hamiltonian, following the formalism of Ref [14], we proved the following theorem.Theorem. For any given even integer N, the ground state 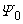 of
of 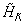 is unique and has quantum numbers n1 = n2 = N/2. Furthermore,
is unique and has quantum numbers n1 = n2 = N/2. Furthermore, 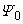 can be written as
can be written as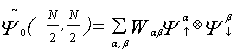 | (7) |
where 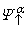 is an orthogonal real basis for one species of N/2 spinless fermions. Take
is an orthogonal real basis for one species of N/2 spinless fermions. Take 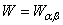 as a
as a 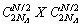 matrix; then W is Hermitian and positive definite.In Ref. [14], the uniqueness of
matrix; then W is Hermitian and positive definite.In Ref. [14], the uniqueness of 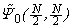 is the consequence of the positive definiteness of W, which was proved under the condition
is the consequence of the positive definiteness of W, which was proved under the condition 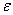 ≠ 0. Ueda et al [15] removed this condition by exploiting a special topology of the PAM in addition to the reflection positivity in the spin space. Consequently the ground state of
≠ 0. Ueda et al [15] removed this condition by exploiting a special topology of the PAM in addition to the reflection positivity in the spin space. Consequently the ground state of 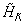 is still non-degenerate even if
is still non-degenerate even if 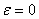 . With knowledge of this fact, we are able to make our proof simpler by introducing H1 and employing Lieb’s theorem, whose proof is more direct. The theorem of Ref. [15] guarantees that the ground state
. With knowledge of this fact, we are able to make our proof simpler by introducing H1 and employing Lieb’s theorem, whose proof is more direct. The theorem of Ref. [15] guarantees that the ground state 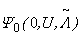 →
→ 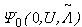 as
as 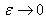 .Theorem 1. Let Ar ≡ frfr . Then, for any two distinct lattice points r and h, we have
.Theorem 1. Let Ar ≡ frfr . Then, for any two distinct lattice points r and h, we have 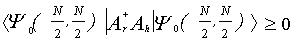 | (8) |
Proof. Taking into account the form of Eq. (7), that is, 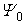 (N/2, N/2), we have
(N/2, N/2), we have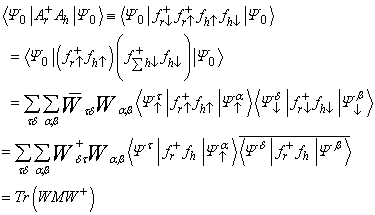 | (9) |
where 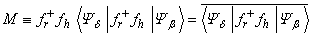 and
and 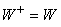
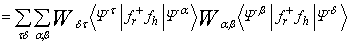 So we have
So we have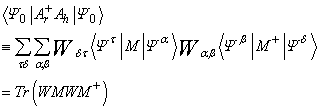 | (10) |
since 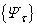 is a real basis.By Lieb’s theorem, W is a positive definite matrix. Consequently, matrix
is a real basis.By Lieb’s theorem, W is a positive definite matrix. Consequently, matrix 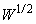 is well defined. Therefore we have
is well defined. Therefore we have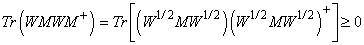 | (11) |
Theorem 1 is proved.Remark 1. It is worthwhile to point out that Theorem 1 has a physical implication. We noticed that 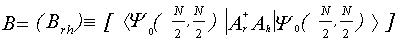 is, in fact, the reduced on-site two-particle density matrix of
is, in fact, the reduced on-site two-particle density matrix of 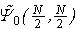 . If the largest eigenvalues
. If the largest eigenvalues 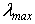 of this matrix satisfies the condition
of this matrix satisfies the condition 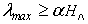 , where
, where 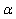 is a positive constant independent of
is a positive constant independent of 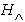 , then
, then 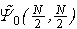 has an off diagonal long-range order (ODLRO), which indicates that
has an off diagonal long-range order (ODLRO), which indicates that 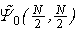 is a superfluid. On the other hand, by Theorem 1, we conclude that, if
is a superfluid. On the other hand, by Theorem 1, we conclude that, if 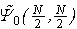 is a superfluid, it must be a Bose – Einstein condensate, namely, a macroscopic on-site pair of electrons that is condensed at p = 0 in
is a superfluid, it must be a Bose – Einstein condensate, namely, a macroscopic on-site pair of electrons that is condensed at p = 0 in 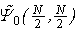 . A detailed analysis on this point is found in Ref. [16].Since Theorem 1 hold for any even integer N, in particular, it holds for the ground state
. A detailed analysis on this point is found in Ref. [16].Since Theorem 1 hold for any even integer N, in particular, it holds for the ground state 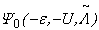 of the negative – (
of the negative – (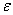 ,U,) symmetric PAM at half filling. Appling the inverse of the particle-hole transformation (6), we immediately obtain the following theorem.Theorem 2: Let
,U,) symmetric PAM at half filling. Appling the inverse of the particle-hole transformation (6), we immediately obtain the following theorem.Theorem 2: Let 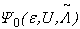 be the ground state of the positive -(
be the ground state of the positive -(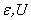 ) symmetric PAM Hamiltonian at half filling. Define the spin operators of the electron by
) symmetric PAM Hamiltonian at half filling. Define the spin operators of the electron by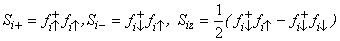 | (12) |
Thus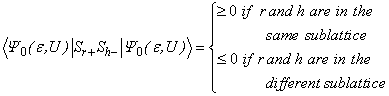 | (13) |
Proof. By the inverse of the unitary particle-hole transformation, we have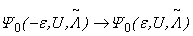
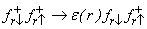 ,
, 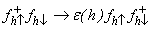 where
where 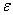 (r) = 1 if r
(r) = 1 if r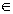 A, and
A, and 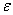 (r) = -1 if r ∈B
(r) = -1 if r ∈B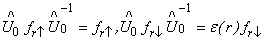 Therefore by Theorem 1,
Therefore by Theorem 1,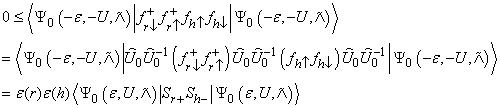 | (15) |
If r and h belong to the same sublattices, then 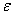 (r)
(r) 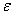 (h) = 1 and hence
(h) = 1 and hence 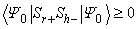 Otherwise,
Otherwise, 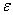 (r)
(r) 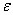 (h) = -1 and
(h) = -1 and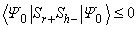 Theorem 2 is proved. Remark 2. The workers in Ref. [17] used the same technique to show the existence of ferrimagnetism in some positive-U Hubbard model.Theorem 2 tells us that the short-range transverse spin correlation of d or f electrons in the ground state of the positive-(
Theorem 2 is proved. Remark 2. The workers in Ref. [17] used the same technique to show the existence of ferrimagnetism in some positive-U Hubbard model.Theorem 2 tells us that the short-range transverse spin correlation of d or f electrons in the ground state of the positive-(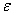 ,U,) symmetric PAM is antiferromagnetic. Since the Hamiltonian
,U,) symmetric PAM is antiferromagnetic. Since the Hamiltonian 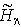 has the SU(2) spin symmetry and its ground state
has the SU(2) spin symmetry and its ground state 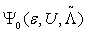 at half filling is nondegenerate, one would expect that Theorem 2 also holds for the longitudinal spin correlation functions. Theorem 3. Let
at half filling is nondegenerate, one would expect that Theorem 2 also holds for the longitudinal spin correlation functions. Theorem 3. Let 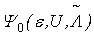 be the ground state of the positive-(
be the ground state of the positive-(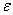 ,U,) symmetric PAM Hamiltonian at half filling. Let
,U,) symmetric PAM Hamiltonian at half filling. Let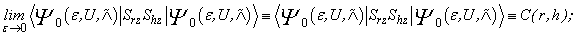 | (16) |
then the spin correlation function C (r, h) has satisfied inequality (13).Proof. We first show that for any pair of distinct lattice points r and h,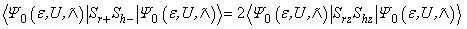 | (17) |
holds.By definition,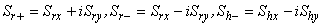 .Therefore we have
.Therefore we have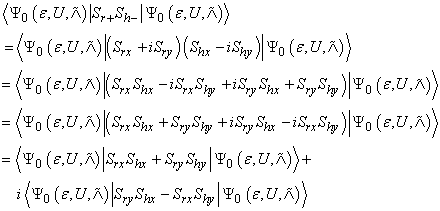 | (18) |
We first simplify the last term on the right-hand side of (18). Since r and h are distinct, [ Srz, Shy] = [ Sry, Shz] = 0. Therefore SryShx - Srx Shy is a Hermitian operator. Consequently, its expectation value in any state is a real quantity. On the other hand, since 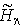 is a real matrix, its ground state
is a real matrix, its ground state 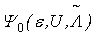 must be chosen as state real vector. Therefore the expectation value F of SryShx - Srx Shy in
must be chosen as state real vector. Therefore the expectation value F of SryShx - Srx Shy in 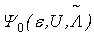 must be a pure imaginary matrix. Consequently F ≡ 0.Next, we apply the unitary operator
must be a pure imaginary matrix. Consequently F ≡ 0.Next, we apply the unitary operator 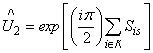 which rotates each spin about the Sz axis by an angle π/2, to the expectation value of Sry Shy in
which rotates each spin about the Sz axis by an angle π/2, to the expectation value of Sry Shy in 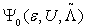 and obtain
and obtain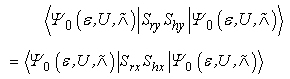 | (19) |
Substituting Eq.(19) into Eq.(18), we obtain the identity in Eq.(17), that is: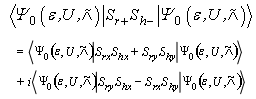 So we have,
So we have,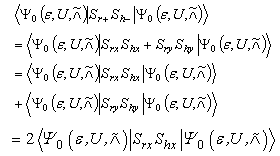 Eq.(17) is proved.Similarly, we can show that
Eq.(17) is proved.Similarly, we can show that 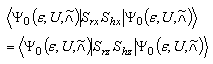 | (20) |
By applying the unitary operator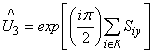 to the expectation value of SrzShz in
to the expectation value of SrzShz in 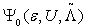 .Combining the identities in Eq.(17) and Eq.(20) and the inequality Eq.(13), we see that the longitudinal spin correlation of
.Combining the identities in Eq.(17) and Eq.(20) and the inequality Eq.(13), we see that the longitudinal spin correlation of 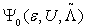 is antiferromagnetic. Since this conclusion is true for any
is antiferromagnetic. Since this conclusion is true for any 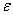 > 0, it must also hold for the limit
> 0, it must also hold for the limit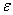 → 0. Therefore the longitudinal spin correlation of the d or f electrons in the ground state of the positive-U symmetric PAM at half filling is antiferromagnetic. Our proof is accomplished.
→ 0. Therefore the longitudinal spin correlation of the d or f electrons in the ground state of the positive-U symmetric PAM at half filling is antiferromagnetic. Our proof is accomplished.
3. Summary and Conclusions
This work is an extension and detailed analysis of Tian article [16] and Ueda et. al. [15] for PAM. We proved the existence of the short – range antiferromagnetic order in the ground state of the symmetric PAM at half filling for arbitrary V and U > 0. We do not claim that the ground state has long – range antiferromagnetic order. In fact it has been shown, by using a mean field slave – boson theory that at the half – filled, the ground state may be either antiferromagnetic or paramagnetic [18]. The line separating their region of stability is given by the critical value of their exchange constant. In all the lattice systems studied recently, it was observed that they have an antiferromagnetic ground state and the first excited state is always a spin singlet [8]. In conclusion, in this paper, we showed rigorously that the spin correlation between (d, d), (f, f), (C, C), (C, d) and (C, f) electrons are antiferromagnetic in the ground state of the PAM at half – fillings. It is often assume that the low-temperature physics of heavy fermion systems is driven solely by AFM interactions. Therefore the heavy-fermion metals offer an interesting playground where magnetism and superconductivity can both compete and coexist [5-6, 19]. The theoretical prove here that the PAM ground state is antiferromagnetic means the model is a good candidate to investigate this competition and co-existence. The will involve investigating the spin correlations of f electrons in the ground state 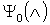 of the PAM which is of fundamental importance but was not discussed in this article. It is hoped that such investigation will be done to ascertain if we can observe in the PAM the growing consensus that the ground state of heavy fermion systems can be either normalconducting, superconducting or magnetically ordered with or without superconductivity. There are currently six heavy fermions compounds having superconducting ground state [20]. In general, the ground state properties of a system are of fundamental importance and the starting point for considering the excitations that enliven real systems [19].
of the PAM which is of fundamental importance but was not discussed in this article. It is hoped that such investigation will be done to ascertain if we can observe in the PAM the growing consensus that the ground state of heavy fermion systems can be either normalconducting, superconducting or magnetically ordered with or without superconductivity. There are currently six heavy fermions compounds having superconducting ground state [20]. In general, the ground state properties of a system are of fundamental importance and the starting point for considering the excitations that enliven real systems [19].
ACKNOWLEDGEMENTS
We appreciate the very useful discussions with J. O. A. Idiodi, B. Iyorzor and S. I. Okunzuwa. EGA acknowledges partial funding by ICBR.
References
| [1] | R. W. Godby and P. García-González (2003) “Density functional theories and self-energy approaches” in 'A Primer in Density Functional Theory’ (edited by Carlos Fiolhais, Fernando Nogueira and M. A. L. Marques) Lecture Notes in Physics Vol. 620, Springer (Heidelberg). |
| [2] | G. E. Akpojotor (2008), “The statistical equivalents of the t-U and t-t-U models” in Lectures on the Physics of Strongly Correlated Systems XII (edited by A. Avella and F. Mancini), AIP Con. Proc. 1014, 251 -259. |
| [3] | G. E. Akpojotor (2008), Possible propagation of the Zhang-Rice singlet as a probable Cooper channel in the CuO2 planes, Physics Letters A 372, 6992 - 6995. |
| [4] | J. C. Amadon and J. E. Hirsch (1997), Metallic ferromagnetism in a single-band model: Effect of band filling and Coulomb interactions, Phys. Rev. B 54, 6364 - 6375. |
| [5] | B. Moller and P. Wolfle (1993). Magnetic Order in the Periodic Anderson Model. Phys. Rev. B 48: 10320 – 10326. |
| [6] | Y. Ōno and K. Mitsumotoa (2006) Heavy fermions in the periodic Anderson model with singlet–triplet crystal-field levels, Physica B: Condensed Matter 378–380, 694–695. |
| [7] | A. Kainz, A. Toschi, R. Peters, K. Held (2012) Kinks in the periodic Anderson model, Phys. Rev. B 86, 195110. |
| [8] | C. M. Varma (2005) Thirty Years of heavy Fermions: Scientific Setting for their Discovery and Partial Understanding, arXiv: 0510019. |
| [9] | K. Kubo (2013) Ferromagnetism and Fermi-surface transition in the periodic Anderson model: Second-order phase transition without symmetry breaking, Phys. Rev. B 87, 195127. |
| [10] | G. D. Mahan (2000). Many Particle Physics. Third Edition, Kluwer Academic/ Plenum, New York, U. S. A. |
| [11] | L. Muhlbacher, F. Urban and A. Komnik (2011). Anderson Impurity Model in Equilibrium: Analytical Results versus quantum Monte Carlo Data. Phys. Rev B 83, 075107 – 075114. |
| [12] | L. Zhu and J. Zhu (2011). Magnetic field induced quantum phase transitions in the two-impurity Anderson model, Phys. Rev. B 83, 245110. |
| [13] | I. Hagymasi, K. Itai and J. Solyom (2013) Quantum criticality and first-order transitions in the extended periodic Anderson model, Phys. Rev. B 87, 125146. |
| [14] | E. H. Lieb (1989). Two Theorems on the Hubbard Model. Phys. Rev. B. 62,1201 – 1204. |
| [15] | K. Ueda, H. Tsunetsugu and M. Sigrist (1992) Singlet Ground State of the Periodic Anderson Model at Half filling: A Rigorous Result. Phys. Rev. Lett.68: 1030 - 1033. |
| [16] | G. S. Tian (1994) Antiferromagnetic order in the periodic Anderson model at half filing: A rigorous result. Phys. Rev. B50: 6246 – 6249. |
| [17] | S. Q. Shen, Z. M. Qiu and G. S. Tian (1994) Ferrimagnetic long-range order of the Hubbard model.Phys. Rev. Lett. 72: 1280 - 1282. |
| [18] | B. Moller and P. Wolfle (1993) Magnetic Order in the Periodic Anderson Model. Phys. Rev. B 48: 10320 – 10326. |
| [19] | S. Nair, O. Stockert, U. Witte, M. Nicklas, R. Schedler, K. Kiefer, J. D. Thompson, A. D. Bianchi, Z. Fisk,,1 S. Wirth,,1 and F. Steglicha (2010) Magnetism and superconductivity driven by identical 4f states in a heavy-fermion metal. Proc Natl Acad Sci U S A, 107(21): 9537 – 9540. |
| [20] | D. Shi and Z. Li (1999) The effect of nonmagnetic doping on the d-wave heavy fermion systems. Commun. Theor. Phys. 31, 205 – 210. |
 with
with 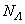 lattice points. Neglecting the orbital degeneracy for the localized electrons, the Hamiltonian of the PAM can be written in the form [9]
lattice points. Neglecting the orbital degeneracy for the localized electrons, the Hamiltonian of the PAM can be written in the form [9]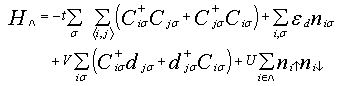
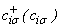 is the creation (annihilation) of electrons, which creates (annihilates) an itinerant electron of spin σ at site i. Similarly,
is the creation (annihilation) of electrons, which creates (annihilates) an itinerant electron of spin σ at site i. Similarly, 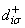 and
and 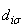 are the fermion operators for the localized electrons.
are the fermion operators for the localized electrons. 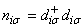 and
and 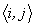 denotes a pair of lattice sites,
denotes a pair of lattice sites, 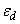 is a local potential, V is the hybridization matrix element and U > 0 represent the on-site Coulomb interaction for the localized electrons.Since its introduction, the PAM and its variants constitute an important research topic in theoretical condensed matter physics, particularly in the context of strongly correlated electron system. Most of the many body techniques commonly used in condensed matter physics can be learnt in this context. Also there are some theoretical tools and concepts which apply to this model only [10-13]. The aim of this paper is to prove that the ground state of the symmetric PAM is a spin singlet.
is a local potential, V is the hybridization matrix element and U > 0 represent the on-site Coulomb interaction for the localized electrons.Since its introduction, the PAM and its variants constitute an important research topic in theoretical condensed matter physics, particularly in the context of strongly correlated electron system. Most of the many body techniques commonly used in condensed matter physics can be learnt in this context. Also there are some theoretical tools and concepts which apply to this model only [10-13]. The aim of this paper is to prove that the ground state of the symmetric PAM is a spin singlet.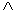 is called bipartite with respect to the Hamiltonian
is called bipartite with respect to the Hamiltonian 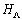 if it can be divided into two sublattices A and B, such that hopping of electrons does not occur between sites in the same sublattices. For a bipartite lattice, the signs of parameters t and V are not important for the mathematical analysis of this Hamiltonian. They can be changed by a unitary transformation. For definiteness, we shall choose t > 0 and V > 0 in the following.To begin with, we first write the Hamiltonian
if it can be divided into two sublattices A and B, such that hopping of electrons does not occur between sites in the same sublattices. For a bipartite lattice, the signs of parameters t and V are not important for the mathematical analysis of this Hamiltonian. They can be changed by a unitary transformation. For definiteness, we shall choose t > 0 and V > 0 in the following.To begin with, we first write the Hamiltonian 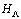 of the symmetric PAM in a generalized Hubbard Hamiltonian. For simplicity, let us consider a specific bipartite lattice: the two-dimensional square lattice
of the symmetric PAM in a generalized Hubbard Hamiltonian. For simplicity, let us consider a specific bipartite lattice: the two-dimensional square lattice 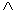 with N = L2 lattice points (the lattice constant is taken to be unity). Take two identical copies of this square lattice,
with N = L2 lattice points (the lattice constant is taken to be unity). Take two identical copies of this square lattice, 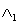 and
and 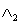 . We make a doubly layered lattice
. We make a doubly layered lattice 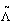 by connecting the corresponding lattice points of
by connecting the corresponding lattice points of 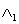 and
and 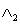 with bonds of length 1. Now, each point of
with bonds of length 1. Now, each point of 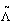 is labelled by r = ( i, m) where m = 1 or 2. Obviously,
is labelled by r = ( i, m) where m = 1 or 2. Obviously, 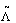 has
has 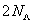 lattice points. Next, we introduce new fermion operators fra by
lattice points. Next, we introduce new fermion operators fra by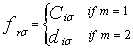
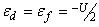 , the Hamiltonian of the PAM is called Symmetric. With the definitions of
, the Hamiltonian of the PAM is called Symmetric. With the definitions of 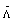 and fra, the Hamiltonian
and fra, the Hamiltonian 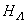 of the symmetric PAM can be rewritten as the Hamiltonian of a generalized Hubbard model on
of the symmetric PAM can be rewritten as the Hamiltonian of a generalized Hubbard model on 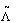 by ignoring an uninteresting constant
by ignoring an uninteresting constant 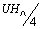 .
.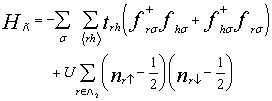

 is still bipartite with respect to
is still bipartite with respect to  . Furthermore, we observe that the electrons in the second layer (the d–electron layer) do not hop and have an on-site Coulomb repulsion, while the electrons in the first layer are itinerant without interaction. To account for this interaction, we introduce an auxiliary interaction operator
. Furthermore, we observe that the electrons in the second layer (the d–electron layer) do not hop and have an on-site Coulomb repulsion, while the electrons in the first layer are itinerant without interaction. To account for this interaction, we introduce an auxiliary interaction operator 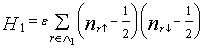
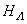 and study the ground state of the new Hamiltonian
and study the ground state of the new Hamiltonian 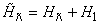 . The
. The 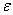 in Equation (5) is a generalized interacting potential so that the interaction can be switched off by letting
in Equation (5) is a generalized interacting potential so that the interaction can be switched off by letting 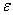 → 0. It is pertinent to point out that this interaction operator in Equation (5) will make it straightforward in future to generalized the proofs here so that by choosing the appropriate interacting elements, we can obtain a generalized Anderson model from which we can in turn also obtain the single site impurity Anderson model and the Kondo model depending on the material system we wish to study. The purposes of the proofs are to show the existence of a short-range antiferromagnetic d-electron spin correlation in the ground state
→ 0. It is pertinent to point out that this interaction operator in Equation (5) will make it straightforward in future to generalized the proofs here so that by choosing the appropriate interacting elements, we can obtain a generalized Anderson model from which we can in turn also obtain the single site impurity Anderson model and the Kondo model depending on the material system we wish to study. The purposes of the proofs are to show the existence of a short-range antiferromagnetic d-electron spin correlation in the ground state 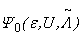 of the positive-(
of the positive-(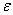 , U) symmetric PAM at half filling. However, reflection positivity in the spin space does not hold in this case. Fortunately, by the well-known unitary particle-hole transformation
, U) symmetric PAM at half filling. However, reflection positivity in the spin space does not hold in this case. Fortunately, by the well-known unitary particle-hole transformation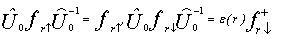
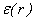 = 1 if r ∈ A and
= 1 if r ∈ A and 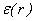 = -1 if r ∈ B, the Hamiltonian is of the same form, which has reflection positivity in the spin space. Obviously, the transformed Hamiltonian has the same spectrum. In the following, we shall first study the ground state
= -1 if r ∈ B, the Hamiltonian is of the same form, which has reflection positivity in the spin space. Obviously, the transformed Hamiltonian has the same spectrum. In the following, we shall first study the ground state 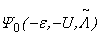 of the Hamiltonian
of the Hamiltonian 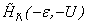 at half filling and then transform it back to the corresponding ground state
at half filling and then transform it back to the corresponding ground state 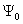 (
(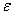 ,
,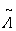 ) of
) of 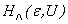 by the inverse of the particle-hole transformation.We observe that
by the inverse of the particle-hole transformation.We observe that 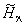 commutes with
commutes with 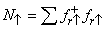 and
and 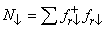 respectively. Consequently, the Hilbert space of
respectively. Consequently, the Hilbert space of 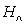 can be divided into numerous subspaces. Each of them is characterized by a pair of integers (N = n1, N= n2). For this Hamiltonian, following the formalism of Ref [14], we proved the following theorem.Theorem. For any given even integer N, the ground state
can be divided into numerous subspaces. Each of them is characterized by a pair of integers (N = n1, N= n2). For this Hamiltonian, following the formalism of Ref [14], we proved the following theorem.Theorem. For any given even integer N, the ground state 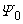 of
of 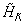 is unique and has quantum numbers n1 = n2 = N/2. Furthermore,
is unique and has quantum numbers n1 = n2 = N/2. Furthermore, 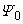 can be written as
can be written as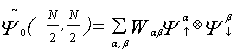
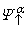 is an orthogonal real basis for one species of N/2 spinless fermions. Take
is an orthogonal real basis for one species of N/2 spinless fermions. Take 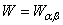 as a
as a 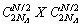 matrix; then W is Hermitian and positive definite.In Ref. [14], the uniqueness of
matrix; then W is Hermitian and positive definite.In Ref. [14], the uniqueness of 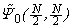 is the consequence of the positive definiteness of W, which was proved under the condition
is the consequence of the positive definiteness of W, which was proved under the condition 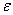 ≠ 0. Ueda et al [15] removed this condition by exploiting a special topology of the PAM in addition to the reflection positivity in the spin space. Consequently the ground state of
≠ 0. Ueda et al [15] removed this condition by exploiting a special topology of the PAM in addition to the reflection positivity in the spin space. Consequently the ground state of 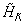 is still non-degenerate even if
is still non-degenerate even if 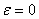 . With knowledge of this fact, we are able to make our proof simpler by introducing H1 and employing Lieb’s theorem, whose proof is more direct. The theorem of Ref. [15] guarantees that the ground state
. With knowledge of this fact, we are able to make our proof simpler by introducing H1 and employing Lieb’s theorem, whose proof is more direct. The theorem of Ref. [15] guarantees that the ground state 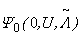 →
→ 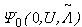 as
as 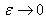 .Theorem 1. Let Ar ≡ frfr . Then, for any two distinct lattice points r and h, we have
.Theorem 1. Let Ar ≡ frfr . Then, for any two distinct lattice points r and h, we have 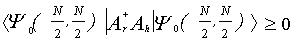
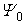 (N/2, N/2), we have
(N/2, N/2), we have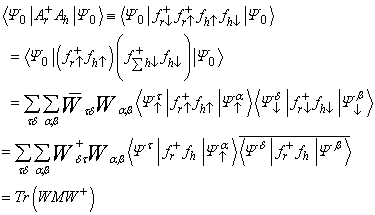
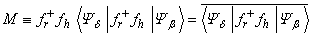 and
and 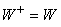
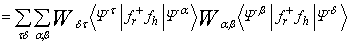 So we have
So we have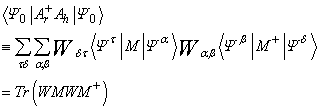
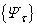 is a real basis.By Lieb’s theorem, W is a positive definite matrix. Consequently, matrix
is a real basis.By Lieb’s theorem, W is a positive definite matrix. Consequently, matrix 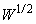 is well defined. Therefore we have
is well defined. Therefore we have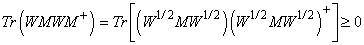
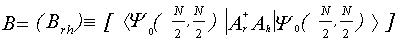 is, in fact, the reduced on-site two-particle density matrix of
is, in fact, the reduced on-site two-particle density matrix of 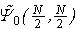 . If the largest eigenvalues
. If the largest eigenvalues 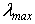 of this matrix satisfies the condition
of this matrix satisfies the condition 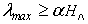 , where
, where 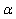 is a positive constant independent of
is a positive constant independent of 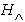 , then
, then 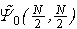 has an off diagonal long-range order (ODLRO), which indicates that
has an off diagonal long-range order (ODLRO), which indicates that 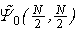 is a superfluid. On the other hand, by Theorem 1, we conclude that, if
is a superfluid. On the other hand, by Theorem 1, we conclude that, if 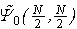 is a superfluid, it must be a Bose – Einstein condensate, namely, a macroscopic on-site pair of electrons that is condensed at p = 0 in
is a superfluid, it must be a Bose – Einstein condensate, namely, a macroscopic on-site pair of electrons that is condensed at p = 0 in 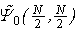 . A detailed analysis on this point is found in Ref. [16].Since Theorem 1 hold for any even integer N, in particular, it holds for the ground state
. A detailed analysis on this point is found in Ref. [16].Since Theorem 1 hold for any even integer N, in particular, it holds for the ground state 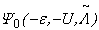 of the negative – (
of the negative – (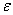 ,U,) symmetric PAM at half filling. Appling the inverse of the particle-hole transformation (6), we immediately obtain the following theorem.Theorem 2: Let
,U,) symmetric PAM at half filling. Appling the inverse of the particle-hole transformation (6), we immediately obtain the following theorem.Theorem 2: Let 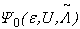 be the ground state of the positive -(
be the ground state of the positive -(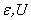 ) symmetric PAM Hamiltonian at half filling. Define the spin operators of the electron by
) symmetric PAM Hamiltonian at half filling. Define the spin operators of the electron by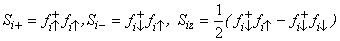
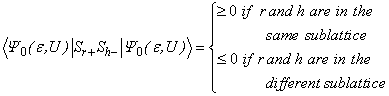
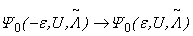
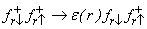 ,
, 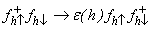 where
where 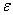 (r) = 1 if r
(r) = 1 if r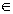 A, and
A, and 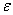 (r) = -1 if r ∈B
(r) = -1 if r ∈B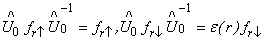 Therefore by Theorem 1,
Therefore by Theorem 1,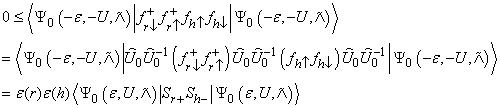
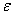 (r)
(r) 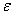 (h) = 1 and hence
(h) = 1 and hence 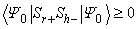 Otherwise,
Otherwise, 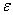 (r)
(r) 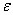 (h) = -1 and
(h) = -1 and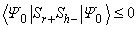 Theorem 2 is proved. Remark 2. The workers in Ref. [17] used the same technique to show the existence of ferrimagnetism in some positive-U Hubbard model.Theorem 2 tells us that the short-range transverse spin correlation of d or f electrons in the ground state of the positive-(
Theorem 2 is proved. Remark 2. The workers in Ref. [17] used the same technique to show the existence of ferrimagnetism in some positive-U Hubbard model.Theorem 2 tells us that the short-range transverse spin correlation of d or f electrons in the ground state of the positive-(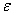 ,U,) symmetric PAM is antiferromagnetic. Since the Hamiltonian
,U,) symmetric PAM is antiferromagnetic. Since the Hamiltonian 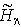 has the SU(2) spin symmetry and its ground state
has the SU(2) spin symmetry and its ground state 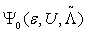 at half filling is nondegenerate, one would expect that Theorem 2 also holds for the longitudinal spin correlation functions. Theorem 3. Let
at half filling is nondegenerate, one would expect that Theorem 2 also holds for the longitudinal spin correlation functions. Theorem 3. Let 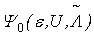 be the ground state of the positive-(
be the ground state of the positive-(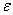 ,U,) symmetric PAM Hamiltonian at half filling. Let
,U,) symmetric PAM Hamiltonian at half filling. Let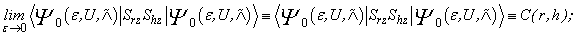
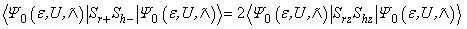
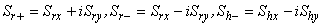 .Therefore we have
.Therefore we have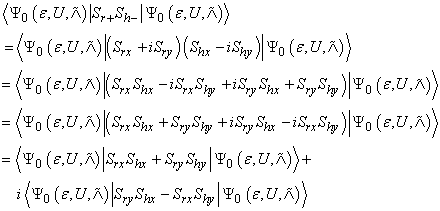
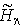 is a real matrix, its ground state
is a real matrix, its ground state 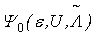 must be chosen as state real vector. Therefore the expectation value F of SryShx - Srx Shy in
must be chosen as state real vector. Therefore the expectation value F of SryShx - Srx Shy in 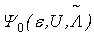 must be a pure imaginary matrix. Consequently F ≡ 0.Next, we apply the unitary operator
must be a pure imaginary matrix. Consequently F ≡ 0.Next, we apply the unitary operator 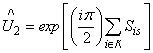 which rotates each spin about the Sz axis by an angle π/2, to the expectation value of Sry Shy in
which rotates each spin about the Sz axis by an angle π/2, to the expectation value of Sry Shy in 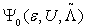 and obtain
and obtain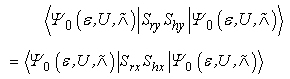
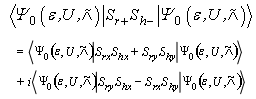 So we have,
So we have,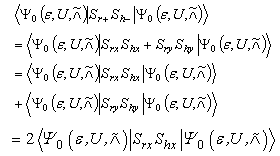 Eq.(17) is proved.Similarly, we can show that
Eq.(17) is proved.Similarly, we can show that 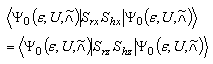
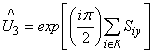 to the expectation value of SrzShz in
to the expectation value of SrzShz in 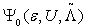 .Combining the identities in Eq.(17) and Eq.(20) and the inequality Eq.(13), we see that the longitudinal spin correlation of
.Combining the identities in Eq.(17) and Eq.(20) and the inequality Eq.(13), we see that the longitudinal spin correlation of 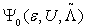 is antiferromagnetic. Since this conclusion is true for any
is antiferromagnetic. Since this conclusion is true for any 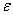 > 0, it must also hold for the limit
> 0, it must also hold for the limit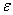 → 0. Therefore the longitudinal spin correlation of the d or f electrons in the ground state of the positive-U symmetric PAM at half filling is antiferromagnetic. Our proof is accomplished.
→ 0. Therefore the longitudinal spin correlation of the d or f electrons in the ground state of the positive-U symmetric PAM at half filling is antiferromagnetic. Our proof is accomplished. 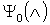 of the PAM which is of fundamental importance but was not discussed in this article. It is hoped that such investigation will be done to ascertain if we can observe in the PAM the growing consensus that the ground state of heavy fermion systems can be either normalconducting, superconducting or magnetically ordered with or without superconductivity. There are currently six heavy fermions compounds having superconducting ground state [20]. In general, the ground state properties of a system are of fundamental importance and the starting point for considering the excitations that enliven real systems [19].
of the PAM which is of fundamental importance but was not discussed in this article. It is hoped that such investigation will be done to ascertain if we can observe in the PAM the growing consensus that the ground state of heavy fermion systems can be either normalconducting, superconducting or magnetically ordered with or without superconductivity. There are currently six heavy fermions compounds having superconducting ground state [20]. In general, the ground state properties of a system are of fundamental importance and the starting point for considering the excitations that enliven real systems [19]. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML