V. N. Soshnikov
Plasma Physics Dept., All-Russian Institute of Scientific and Technical Information of the Russian Academy of Sciences (VINITI), Usievitcha 20, 125315 Moscow, Russia
Correspondence to: V. N. Soshnikov, Plasma Physics Dept., All-Russian Institute of Scientific and Technical Information of the Russian Academy of Sciences (VINITI), Usievitcha 20, 125315 Moscow, Russia.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The so-called Landau damping of electron waves in collisionless plasma does not exist due to the fact that when tending to zero the decrement 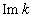 in
in 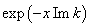 characterizing the spatial wave damping, real part of divergent integral in the corresponding dispersion equation remains finite, making unnecessary addition to the complex dispersion equation the complex residue of the pole of the integral with logarithmical divergence in singularity point
characterizing the spatial wave damping, real part of divergent integral in the corresponding dispersion equation remains finite, making unnecessary addition to the complex dispersion equation the complex residue of the pole of the integral with logarithmical divergence in singularity point 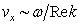 at
at 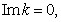 where
where 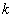 is complex wave number,
is complex wave number, 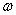 is frequency, hence the collisionless Landau damping is resulting in violation of the law of energy conservation, causes problems with the rule of bypass around the pole in the calculation of the imaginary residue in the singularity point, leads to exponentially divergent solutions at
is frequency, hence the collisionless Landau damping is resulting in violation of the law of energy conservation, causes problems with the rule of bypass around the pole in the calculation of the imaginary residue in the singularity point, leads to exponentially divergent solutions at 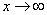 and other logical contradictions. The divergence of the imaginary part of dispersion relation at
and other logical contradictions. The divergence of the imaginary part of dispersion relation at 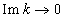 with the existence of solutions in the case
with the existence of solutions in the case 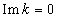 is already the reason for discarding solutions with
is already the reason for discarding solutions with 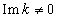 . A relation is established between the averaged over oscillation period wave damping decrement and the collision term of kinetic equation. Collisionless Vlasov-Landau damping is explained finally by inadequate using mathematically correct results of transformations the nonlinear complex expressions.
. A relation is established between the averaged over oscillation period wave damping decrement and the collision term of kinetic equation. Collisionless Vlasov-Landau damping is explained finally by inadequate using mathematically correct results of transformations the nonlinear complex expressions.
Keywords:
Weakly collisional plasma waves, Landau damping, Collision damping, Collisiomless damping
Cite this paper: V. N. Soshnikov, On the Wave Damping in Weakly Collisional Plasma, International Journal of Theoretical and Mathematical Physics, Vol. 4 No. 2, 2014, pp. 58-62. doi: 10.5923/j.ijtmp.20140402.04.
1. Introduction
Collisionless Landau damping is described in all textbooks on plasma physics as theoretically long ago predicted physical phenomenon of exponentially damping / growing electron waves in collisionless plasma [1], [2]. Theoretical deriving is based on the substitution of solutions in the form of complex running waves into the field equation and the kinetic equation with finding complex roots of the resulting complex dispersion equation, for example, for a given real frequency  , where
, where 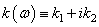 and
and 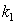 is wave number,
is wave number, 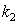 is decrement/increment of the electron wave. In this case the wave damping/growing is not consistent with the law of energy conservation and leads to a number of other contradictions [3].Substitution into the original equations the real waves of the form
is decrement/increment of the electron wave. In this case the wave damping/growing is not consistent with the law of energy conservation and leads to a number of other contradictions [3].Substitution into the original equations the real waves of the form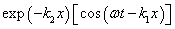 and
and 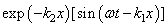 leads to real dispersion equation containing two parameters
leads to real dispersion equation containing two parameters 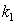 and
and 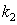 to be determined and (at given
to be determined and (at given 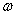 ) the need to add the second equation which naturally is the equation of energy conservation with addition the energy-exchange collision term to the kinetic equation. It is shown that in the absence of such term the collisionless damping, which corresponds to the solution
) the need to add the second equation which naturally is the equation of energy conservation with addition the energy-exchange collision term to the kinetic equation. It is shown that in the absence of such term the collisionless damping, which corresponds to the solution 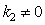 , does not exist.
, does not exist.
2. Analysis in Complex Variables
The well known solution for the electron velocity distribution function when considering electron waves in collisionless plasma is sought in the form of addition to the Maxwell electron distribution 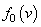 the complex distribution function (with real
the complex distribution function (with real 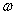 )
)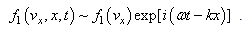 | (1) |
After its substitution to the collisionless kinetic equation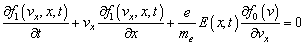 | (2) |
we obtain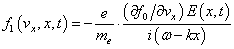 | (3) |
where the complex electric field in Maxwell equation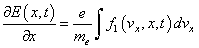 | (4) |
is assumed to be equal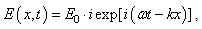 | (5) |
and 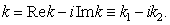 The complex dispersion equation
The complex dispersion equation 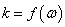 corresponding to these values contains logarithmically divergent integral of the form at
corresponding to these values contains logarithmically divergent integral of the form at 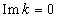
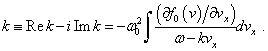 | (6) |
This leads to the relation between the actual observed real parameters of the real part of the dispersion equation 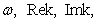 where
where 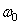 is Langmuir frequency
is Langmuir frequency 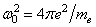 and
and 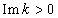 characterizes the wave damping
characterizes the wave damping 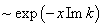
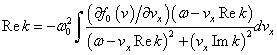 | (7) |
with the real part of the electric field (5) in the plane 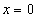
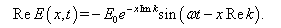 | (8) |
Virtual imaginary part of the dispersion equation 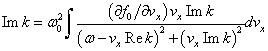 | (9) |
leads when 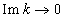 either to identity
either to identity 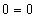 or to the divergent integral
or to the divergent integral 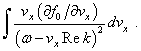 | (10) |
The latter result with the strange damping/growing solution 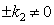 (which follows from the complex form of the Vlasov equations, “Vlasov damping” (9) at
(which follows from the complex form of the Vlasov equations, “Vlasov damping” (9) at 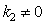 , see also [3]) violating the energy conservation law, and the impossibility of the smooth transition
, see also [3]) violating the energy conservation law, and the impossibility of the smooth transition 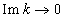 indicates the inadequacy of using nonlinear complex expressions unrelated to the energy conservation law to describe the relationships between real physical quantities with a side effect of working with complex nonlinear equations.But at the same time to each given value
indicates the inadequacy of using nonlinear complex expressions unrelated to the energy conservation law to describe the relationships between real physical quantities with a side effect of working with complex nonlinear equations.But at the same time to each given value 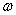 there corresponds the root of the complex dispersion equation with
there corresponds the root of the complex dispersion equation with 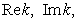 that is collisionless damping with
that is collisionless damping with 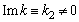 , while without having need to add a residuum/halfresiduum of any absent pole to the finite at
, while without having need to add a residuum/halfresiduum of any absent pole to the finite at 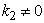 integral (9).
integral (9).
3. Analysis in Real Variables
With direct substitution of initially real values 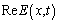 and
and 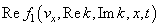 (in which
(in which 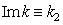 determines the wave damping
determines the wave damping 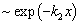 ) in the kinetic and Maxwell equations we obtain real dispersion equation in different form
) in the kinetic and Maxwell equations we obtain real dispersion equation in different form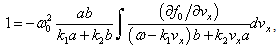 | (11) |
where we use the notation 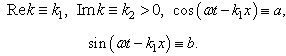 | (12) |
Since the dispersion equation contains two unknown variables 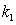 ,
, 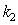 , to determine them one needs to add an independent energy conservation equation of collisional energy balance. However, the exact damping solution with independent of
, to determine them one needs to add an independent energy conservation equation of collisional energy balance. However, the exact damping solution with independent of 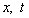 values
values 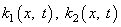 even neglecting derivatives
even neglecting derivatives 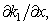
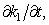
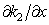 ,
, 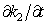 of the next order of smallness (e.g., even by using the some average values
of the next order of smallness (e.g., even by using the some average values 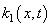 and
and 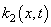 ) does not exist in this somewhat artificial initial formulation of the problem for any
) does not exist in this somewhat artificial initial formulation of the problem for any 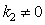 due to integrand terms with
due to integrand terms with 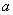 and
and 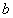 .This dispersion equation is analogous to equation (7) only if
.This dispersion equation is analogous to equation (7) only if 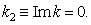 Its distinction from the equation (7) can be understood by comparing with the elementary illustrative example of nonlinear inequality for arbitrary real values
Its distinction from the equation (7) can be understood by comparing with the elementary illustrative example of nonlinear inequality for arbitrary real values 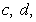
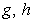 :
: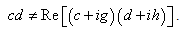 | (13) |
The right hand side of (13) contains mixed term 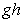 and mixed imaginary terms whose appearance has nothing to do with physical nature of all values and their mutual relations (for example, in the case of the law of energy conservation). However, Eq. (11) is similar in form to the above expression (7). That is, even at cutting off the distribution function
and mixed imaginary terms whose appearance has nothing to do with physical nature of all values and their mutual relations (for example, in the case of the law of energy conservation). However, Eq. (11) is similar in form to the above expression (7). That is, even at cutting off the distribution function 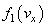 in accordance with the condition of positivity of the total distribution function
in accordance with the condition of positivity of the total distribution function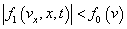 | (14) |
and at 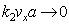 , we obtain dispersion integral in the principal value sense with non-damping wave.As a first step of the process of finding damping solution one can use some non zero value
, we obtain dispersion integral in the principal value sense with non-damping wave.As a first step of the process of finding damping solution one can use some non zero value 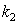 , but the collision term in kinetic equation of the type
, but the collision term in kinetic equation of the type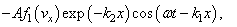 | (15) |
should be added then to the right hand side of kinetic equation with which the dispersion equation becomes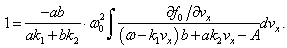 | (16) |
In the process of tending 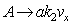 the dispersion integral is finite, which corresponds to its calculation in the principal value sense in analogy with the expression (7).Apparent internal contradiction is that in a hypothetical Landau damping with
the dispersion integral is finite, which corresponds to its calculation in the principal value sense in analogy with the expression (7).Apparent internal contradiction is that in a hypothetical Landau damping with 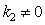 , even without cutting off
, even without cutting off 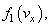 the dispersion integral is finite, and in the absence of poles of the integrand (11) any need to add imaginary residua / halfresidua to dispersion integral that leads to Landau damping is completely absent.In this simplified initial formulation of the problem (11) the dependences of
the dispersion integral is finite, and in the absence of poles of the integrand (11) any need to add imaginary residua / halfresidua to dispersion integral that leads to Landau damping is completely absent.In this simplified initial formulation of the problem (11) the dependences of 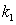 and
and 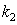 on
on 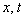 can not be calculated (the problem is insoluble), but apparently possibility exists of their calculation in the approach of averages values. The main result of the made analysis is proof that the so-called Landau damping does not exist as a real natural phenomenon.It is possible, however, to obtain the averaged over oscillations value
can not be calculated (the problem is insoluble), but apparently possibility exists of their calculation in the approach of averages values. The main result of the made analysis is proof that the so-called Landau damping does not exist as a real natural phenomenon.It is possible, however, to obtain the averaged over oscillations value 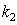 , at least approximately for
, at least approximately for 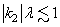 , where
, where 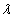 is wave length
is wave length 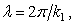 by setting
by setting 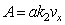 with
with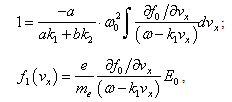 | (17) |
where expression 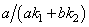 is replaced by the value averaged over the oscillation period
is replaced by the value averaged over the oscillation period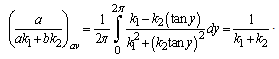 | (18) |
Average value 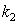 should be determined independently by the integral law of energy conservation, respectively, it could be large enough in (7), (9) to satisfy condition (14), but it can be small, and then one should implement cutting off function
should be determined independently by the integral law of energy conservation, respectively, it could be large enough in (7), (9) to satisfy condition (14), but it can be small, and then one should implement cutting off function 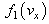 according to condition (14) which is necessary, unlike (7), in any case, according to the expression (17). Parameter
according to condition (14) which is necessary, unlike (7), in any case, according to the expression (17). Parameter 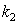 is crucial factor in the proof of non-existence of collisionless damping (contrary to the collisionless Landau damping) at the apparent absence of collisional terms in kinetic equation and determines very small collisional damping of the wave and of the electric field in plasma at
is crucial factor in the proof of non-existence of collisionless damping (contrary to the collisionless Landau damping) at the apparent absence of collisional terms in kinetic equation and determines very small collisional damping of the wave and of the electric field in plasma at 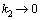 when taking into account the real-life small collision additives to the kinetic equation in the form determined by the balance energy parameter
when taking into account the real-life small collision additives to the kinetic equation in the form determined by the balance energy parameter 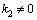 .Integral (17) is calculated in the principal value sense that corresponds to the form of the integral (7) obtained using complex variables.It is inconceivable that there would not be arbitrarily small wave damping in the presence of arbitrarily small but non-zero terms of collisional kinetic equation.Thus, it is clear that we obtain by (16) or (17) at
.Integral (17) is calculated in the principal value sense that corresponds to the form of the integral (7) obtained using complex variables.It is inconceivable that there would not be arbitrarily small wave damping in the presence of arbitrarily small but non-zero terms of collisional kinetic equation.Thus, it is clear that we obtain by (16) or (17) at 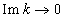 not-damping collisionless Vlasov solution [1] with the integral in the principal value sense, hence proposed by Landau [2] eight years later adding to the complex Vlasov dispersion equation the imaginary residue at the pole
not-damping collisionless Vlasov solution [1] with the integral in the principal value sense, hence proposed by Landau [2] eight years later adding to the complex Vlasov dispersion equation the imaginary residue at the pole 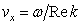 leading to the so-called Landau damping is erroneous. The real problem is to find the roots of a complex dispersion equation without any artificial additives.Due to the smallness of the range
leading to the so-called Landau damping is erroneous. The real problem is to find the roots of a complex dispersion equation without any artificial additives.Due to the smallness of the range 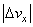 near the singularity point
near the singularity point 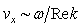 and smallness
and smallness 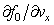 at large
at large 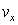 , corrections due to the missing collision term in the kinetic equation influence usually very weakly on the solution of the dispersion equations (16), (17), however obtaining solution for
, corrections due to the missing collision term in the kinetic equation influence usually very weakly on the solution of the dispersion equations (16), (17), however obtaining solution for 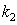 requires to attract additional new equation (since the dispersion equation contains at least two parameters
requires to attract additional new equation (since the dispersion equation contains at least two parameters 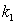 and
and 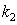 to be determined) which takes into account the energy loss in collisions of electrons with each other and with atoms and molecules present in plasma.In computing, for example, the modulated flux of electrons entrained by non-damping Van Kampen waves at
to be determined) which takes into account the energy loss in collisions of electrons with each other and with atoms and molecules present in plasma.In computing, for example, the modulated flux of electrons entrained by non-damping Van Kampen waves at 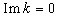 it is necessary to carry out a smooth cutoff of the distribution function
it is necessary to carry out a smooth cutoff of the distribution function 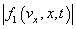 near the critical point
near the critical point 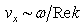 in accordance with the condition (14). Integral energy balance can be written, for example, as relation of the type
in accordance with the condition (14). Integral energy balance can be written, for example, as relation of the type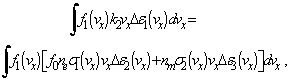 | (19) |
where 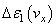 is energy loss per electron associated with a decrease in the number of electrons with an additional wave propagation velocity
is energy loss per electron associated with a decrease in the number of electrons with an additional wave propagation velocity 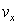 ;
; 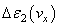 ,
, 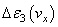 are portions of transmitted energy;
are portions of transmitted energy; 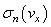 are collision cross sections;
are collision cross sections; 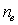 is electron density;
is electron density; 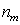 is density of atoms and molecules. In this
is density of atoms and molecules. In this 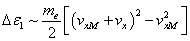 | (20) |
where 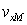 is proper velocity of electron along the axis
is proper velocity of electron along the axis 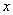 in Maxwell distribution
in Maxwell distribution 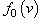 independent on the wave speed. In expression (19) one can add also any other energy-exchange processes.It is assumed that at extreme complexity of calculations using original kinetic equation, the proposed approximations with averaging
independent on the wave speed. In expression (19) one can add also any other energy-exchange processes.It is assumed that at extreme complexity of calculations using original kinetic equation, the proposed approximations with averaging 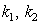 and calculation averaged
and calculation averaged 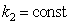 based on the energy balance represent the main features of the damping plasma waves. A more detailed exposition is presented in [3], where are marked some obvious logical contradictions that arise when using Landau rules: violation of the energy conservation law in the damping waves; the appearance of exponentially divergent solution at
based on the energy balance represent the main features of the damping plasma waves. A more detailed exposition is presented in [3], where are marked some obvious logical contradictions that arise when using Landau rules: violation of the energy conservation law in the damping waves; the appearance of exponentially divergent solution at 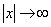 ; uncertainties in calculating the residue or the half residue near/on the real axis of the wave velocity
; uncertainties in calculating the residue or the half residue near/on the real axis of the wave velocity 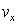 ; jump transition between the non-zero values of the damping parameter
; jump transition between the non-zero values of the damping parameter 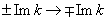 when choosing the bypass direction around the pole (cf. inspiring causality principle in [4]) or at infinitesimal displacement of the pole across the real axis
when choosing the bypass direction around the pole (cf. inspiring causality principle in [4]) or at infinitesimal displacement of the pole across the real axis 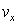 ; contradictions of the calculating residue or half residue at the pole.
; contradictions of the calculating residue or half residue at the pole.
4. Conclusions
There is considered general ideology of solving the problem of wave propagation in a collisionless plasma with the phenomenological account of collisional damping parameter (decrement) 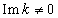 determined by collision term in the kinetic equation, with the substantiation of impossibility of collisionless Landau damping, which leads to a number of obvious logical contradictions [3]. Thereby: 1. Using technology of complex variables to solve the equations for waves
determined by collision term in the kinetic equation, with the substantiation of impossibility of collisionless Landau damping, which leads to a number of obvious logical contradictions [3]. Thereby: 1. Using technology of complex variables to solve the equations for waves 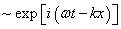 with complex
with complex 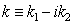 ,
, 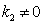 leads to results that are not equivalent to the solution of equations with real physical variables and waves Nonlinear complex expressions lead to errors in the transition to the real relations of physically observable real quantities with violation energy conservation law.2. Smoothed transition to the singularity point
leads to results that are not equivalent to the solution of equations with real physical variables and waves Nonlinear complex expressions lead to errors in the transition to the real relations of physically observable real quantities with violation energy conservation law.2. Smoothed transition to the singularity point 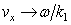 in which the real integrand of the real dispersion integral remains finite for any values
in which the real integrand of the real dispersion integral remains finite for any values 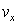 arbitrarily close to
arbitrarily close to 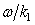 leads to the dispersion integral in the principal value sense without the need to supplement it with imaginary residue at the singularity point.3. Moreover, the requirement of positivity of the total distribution function (14) leads to the necessity of its cutting off near the singularity point with resulting the finite integrand and the finite dispersion integral.4. When adding collision terms into the kinetic equation, surprisingly simple and natural averaging of the real dispersion equation over the period of oscillations leads to the dispersion equation for the two unknown parameters
leads to the dispersion integral in the principal value sense without the need to supplement it with imaginary residue at the singularity point.3. Moreover, the requirement of positivity of the total distribution function (14) leads to the necessity of its cutting off near the singularity point with resulting the finite integrand and the finite dispersion integral.4. When adding collision terms into the kinetic equation, surprisingly simple and natural averaging of the real dispersion equation over the period of oscillations leads to the dispersion equation for the two unknown parameters 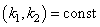 .5. The second equation (19) to determine the values
.5. The second equation (19) to determine the values 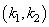 is averaged over the period
is averaged over the period 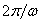 energy balance equation, and the exponential damping of the wave at arbitrarily infinitesimal collision term can lead to arbitrarily infinitesimal value
energy balance equation, and the exponential damping of the wave at arbitrarily infinitesimal collision term can lead to arbitrarily infinitesimal value 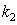 .6. In the case of the collisionless plasma such averaging in (11) is not possible, and the solution of the dispersion equation (11) with
.6. In the case of the collisionless plasma such averaging in (11) is not possible, and the solution of the dispersion equation (11) with 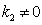 and exponentially damping wave with
and exponentially damping wave with 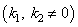 does not exist.Thus, the main results are: (1) nonphysical negative electron distribution functions must be cut off, what leads to elimination of singular points in the dispersion equation; (2) the use of complex expressions for the wave functions with solving nonlinear complex dispersion equation leads to erroneous relations between physically observable real wave parameters and the emergence of collisionless damping; (3) solving the real wave dispersion equation with constant parameters
does not exist.Thus, the main results are: (1) nonphysical negative electron distribution functions must be cut off, what leads to elimination of singular points in the dispersion equation; (2) the use of complex expressions for the wave functions with solving nonlinear complex dispersion equation leads to erroneous relations between physically observable real wave parameters and the emergence of collisionless damping; (3) solving the real wave dispersion equation with constant parameters 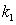 and
and 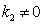 (at constant real
(at constant real 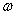 ) is possible only when averaged over the period oscillation values
) is possible only when averaged over the period oscillation values 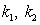 . At the same time their determination requires the addition of the second equation with
. At the same time their determination requires the addition of the second equation with 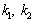 , which may be an energy balance equation when adding collisional terms in kinetic equation.Carried out in this paper relatively very simple analysis leads to the conclusion that an analytical description of the damping/growing electron waves in plasma is impossible without adding appropriate collision (energy-exchange) terms in the collisionless kinetic equation.The principal result of this paper is demonstration of the serious consequences of commonly used in physics of wave processes in weak collisional plasma the techniques in the form of mathematically correct transformations of nonlinear complex expressions that leads to completely erroneous conclusions about the true relations of real physical observables. In particular, values
, which may be an energy balance equation when adding collisional terms in kinetic equation.Carried out in this paper relatively very simple analysis leads to the conclusion that an analytical description of the damping/growing electron waves in plasma is impossible without adding appropriate collision (energy-exchange) terms in the collisionless kinetic equation.The principal result of this paper is demonstration of the serious consequences of commonly used in physics of wave processes in weak collisional plasma the techniques in the form of mathematically correct transformations of nonlinear complex expressions that leads to completely erroneous conclusions about the true relations of real physical observables. In particular, values 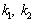 in Eq. (11) depend on
in Eq. (11) depend on 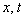 unlike equations (7), (9).These results are correction of the author's comment pp. 515 - 516 to the Russian translation of [5]. Trivial explanation of many-years ambiguities of Vlasov-Landau wave damping in weakly collisional plasma by uncritical using results of transformations the complex nonlinear equations is shocking. There is the open question: whether now Landau damping is considered and can be considered as an outstanding discovery of plasma physics?
unlike equations (7), (9).These results are correction of the author's comment pp. 515 - 516 to the Russian translation of [5]. Trivial explanation of many-years ambiguities of Vlasov-Landau wave damping in weakly collisional plasma by uncritical using results of transformations the complex nonlinear equations is shocking. There is the open question: whether now Landau damping is considered and can be considered as an outstanding discovery of plasma physics?
References
| [1] | Vlasov A. A. On vibration properties of electron gas. JETP (USSR), 1938, 8, p. 291 (in Russian); Uspekhi Fiz. Nauk, 1967, 93, pp. 444 - 470 (reprint, in Russian) (there is English Ed.). |
| [2] | Landau L. D. On electron plasma oscillations. JETP (USSR), 1946, 16, p. 574 (in Russian); Uspekhi Fiz. Nauk, 1967, 93, pp. 527 – 540 (reprint, in Russian) (there is English Ed.). |
| [3] | Soshnikov V. N. Logical contradictions of Landau damping. ArXiv.org/physics/0610220. |
| [4] | Кадомцев В. В. Коллективные явления в плазме. (Collective phenomena in plasmas, in Russian). “Наука”, 2-е изд., Mосква, 1988, с.304. |
| [5] | Clemmow P. C., Dougherty J. P. Electrodynamics of Particles and Plasmas. Addison-Wesley, 1969; 1990. (There is Russian translation: Ф. Клеммоу, Дж. Доуэрти. Электродинамика частиц и плазмы. М. Изд. “Мир”, 1996). |

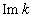 in
in 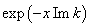 characterizing the spatial wave damping, real part of divergent integral in the corresponding dispersion equation remains finite, making unnecessary addition to the complex dispersion equation the complex residue of the pole of the integral with logarithmical divergence in singularity point
characterizing the spatial wave damping, real part of divergent integral in the corresponding dispersion equation remains finite, making unnecessary addition to the complex dispersion equation the complex residue of the pole of the integral with logarithmical divergence in singularity point 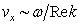 at
at 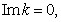 where
where 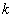 is complex wave number,
is complex wave number, 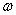 is frequency, hence the collisionless Landau damping is resulting in violation of the law of energy conservation, causes problems with the rule of bypass around the pole in the calculation of the imaginary residue in the singularity point, leads to exponentially divergent solutions at
is frequency, hence the collisionless Landau damping is resulting in violation of the law of energy conservation, causes problems with the rule of bypass around the pole in the calculation of the imaginary residue in the singularity point, leads to exponentially divergent solutions at 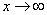 and other logical contradictions. The divergence of the imaginary part of dispersion relation at
and other logical contradictions. The divergence of the imaginary part of dispersion relation at 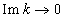 with the existence of solutions in the case
with the existence of solutions in the case 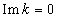 is already the reason for discarding solutions with
is already the reason for discarding solutions with 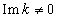 . A relation is established between the averaged over oscillation period wave damping decrement and the collision term of kinetic equation. Collisionless Vlasov-Landau damping is explained finally by inadequate using mathematically correct results of transformations the nonlinear complex expressions.
. A relation is established between the averaged over oscillation period wave damping decrement and the collision term of kinetic equation. Collisionless Vlasov-Landau damping is explained finally by inadequate using mathematically correct results of transformations the nonlinear complex expressions.
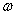 , where
, where 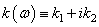 and
and 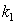 is wave number,
is wave number, 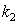 is decrement/increment of the electron wave. In this case the wave damping/growing is not consistent with the law of energy conservation and leads to a number of other contradictions [3].Substitution into the original equations the real waves of the form
is decrement/increment of the electron wave. In this case the wave damping/growing is not consistent with the law of energy conservation and leads to a number of other contradictions [3].Substitution into the original equations the real waves of the form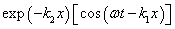 and
and 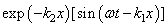 leads to real dispersion equation containing two parameters
leads to real dispersion equation containing two parameters 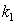 and
and 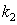 to be determined and (at given
to be determined and (at given 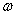 ) the need to add the second equation which naturally is the equation of energy conservation with addition the energy-exchange collision term to the kinetic equation. It is shown that in the absence of such term the collisionless damping, which corresponds to the solution
) the need to add the second equation which naturally is the equation of energy conservation with addition the energy-exchange collision term to the kinetic equation. It is shown that in the absence of such term the collisionless damping, which corresponds to the solution 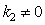 , does not exist.
, does not exist.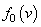 the complex distribution function (with real
the complex distribution function (with real 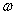 )
)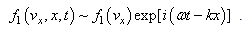
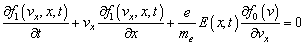
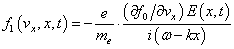
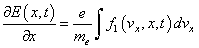
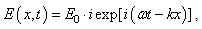
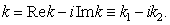 The complex dispersion equation
The complex dispersion equation 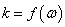 corresponding to these values contains logarithmically divergent integral of the form at
corresponding to these values contains logarithmically divergent integral of the form at 
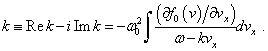
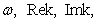 where
where 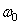 is Langmuir frequency
is Langmuir frequency 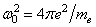 and
and 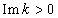 characterizes the wave damping
characterizes the wave damping 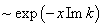
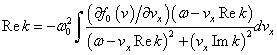
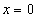
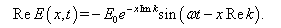
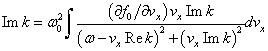
 either to identity
either to identity  or to the divergent integral
or to the divergent integral 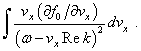
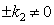 (which follows from the complex form of the Vlasov equations, “Vlasov damping” (9) at
(which follows from the complex form of the Vlasov equations, “Vlasov damping” (9) at 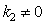 , see also [3]) violating the energy conservation law, and the impossibility of the smooth transition
, see also [3]) violating the energy conservation law, and the impossibility of the smooth transition 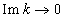 indicates the inadequacy of using nonlinear complex expressions unrelated to the energy conservation law to describe the relationships between real physical quantities with a side effect of working with complex nonlinear equations.But at the same time to each given value
indicates the inadequacy of using nonlinear complex expressions unrelated to the energy conservation law to describe the relationships between real physical quantities with a side effect of working with complex nonlinear equations.But at the same time to each given value 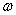 there corresponds the root of the complex dispersion equation with
there corresponds the root of the complex dispersion equation with 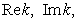 that is collisionless damping with
that is collisionless damping with 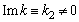 , while without having need to add a residuum/halfresiduum of any absent pole to the finite at
, while without having need to add a residuum/halfresiduum of any absent pole to the finite at 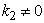 integral (9).
integral (9).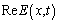 and
and 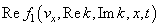 (in which
(in which 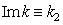 determines the wave damping
determines the wave damping 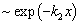 ) in the kinetic and Maxwell equations we obtain real dispersion equation in different form
) in the kinetic and Maxwell equations we obtain real dispersion equation in different form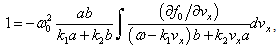
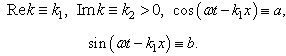
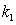 ,
, 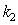 , to determine them one needs to add an independent energy conservation equation of collisional energy balance. However, the exact damping solution with independent of
, to determine them one needs to add an independent energy conservation equation of collisional energy balance. However, the exact damping solution with independent of 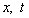 values
values 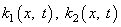 even neglecting derivatives
even neglecting derivatives 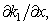
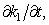
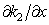 ,
, 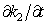 of the next order of smallness (e.g., even by using the some average values
of the next order of smallness (e.g., even by using the some average values 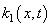 and
and 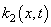 ) does not exist in this somewhat artificial initial formulation of the problem for any
) does not exist in this somewhat artificial initial formulation of the problem for any 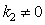 due to integrand terms with
due to integrand terms with 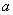 and
and 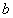 .This dispersion equation is analogous to equation (7) only if
.This dispersion equation is analogous to equation (7) only if 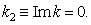 Its distinction from the equation (7) can be understood by comparing with the elementary illustrative example of nonlinear inequality for arbitrary real values
Its distinction from the equation (7) can be understood by comparing with the elementary illustrative example of nonlinear inequality for arbitrary real values 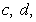
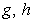 :
: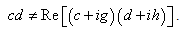
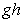 and mixed imaginary terms whose appearance has nothing to do with physical nature of all values and their mutual relations (for example, in the case of the law of energy conservation). However, Eq. (11) is similar in form to the above expression (7). That is, even at cutting off the distribution function
and mixed imaginary terms whose appearance has nothing to do with physical nature of all values and their mutual relations (for example, in the case of the law of energy conservation). However, Eq. (11) is similar in form to the above expression (7). That is, even at cutting off the distribution function 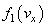 in accordance with the condition of positivity of the total distribution function
in accordance with the condition of positivity of the total distribution function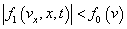
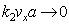 , we obtain dispersion integral in the principal value sense with non-damping wave.As a first step of the process of finding damping solution one can use some non zero value
, we obtain dispersion integral in the principal value sense with non-damping wave.As a first step of the process of finding damping solution one can use some non zero value 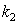 , but the collision term in kinetic equation of the type
, but the collision term in kinetic equation of the type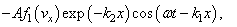
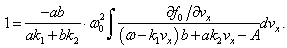
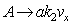 the dispersion integral is finite, which corresponds to its calculation in the principal value sense in analogy with the expression (7).Apparent internal contradiction is that in a hypothetical Landau damping with
the dispersion integral is finite, which corresponds to its calculation in the principal value sense in analogy with the expression (7).Apparent internal contradiction is that in a hypothetical Landau damping with 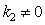 , even without cutting off
, even without cutting off 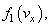 the dispersion integral is finite, and in the absence of poles of the integrand (11) any need to add imaginary residua / halfresidua to dispersion integral that leads to Landau damping is completely absent.In this simplified initial formulation of the problem (11) the dependences of
the dispersion integral is finite, and in the absence of poles of the integrand (11) any need to add imaginary residua / halfresidua to dispersion integral that leads to Landau damping is completely absent.In this simplified initial formulation of the problem (11) the dependences of 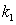 and
and 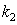 on
on 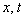 can not be calculated (the problem is insoluble), but apparently possibility exists of their calculation in the approach of averages values. The main result of the made analysis is proof that the so-called Landau damping does not exist as a real natural phenomenon.It is possible, however, to obtain the averaged over oscillations value
can not be calculated (the problem is insoluble), but apparently possibility exists of their calculation in the approach of averages values. The main result of the made analysis is proof that the so-called Landau damping does not exist as a real natural phenomenon.It is possible, however, to obtain the averaged over oscillations value 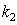 , at least approximately for
, at least approximately for 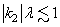 , where
, where 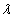 is wave length
is wave length 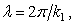 by setting
by setting 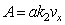 with
with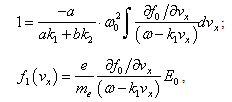
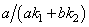 is replaced by the value averaged over the oscillation period
is replaced by the value averaged over the oscillation period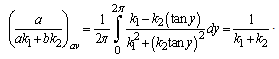
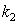 should be determined independently by the integral law of energy conservation, respectively, it could be large enough in (7), (9) to satisfy condition (14), but it can be small, and then one should implement cutting off function
should be determined independently by the integral law of energy conservation, respectively, it could be large enough in (7), (9) to satisfy condition (14), but it can be small, and then one should implement cutting off function 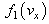 according to condition (14) which is necessary, unlike (7), in any case, according to the expression (17). Parameter
according to condition (14) which is necessary, unlike (7), in any case, according to the expression (17). Parameter 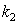 is crucial factor in the proof of non-existence of collisionless damping (contrary to the collisionless Landau damping) at the apparent absence of collisional terms in kinetic equation and determines very small collisional damping of the wave and of the electric field in plasma at
is crucial factor in the proof of non-existence of collisionless damping (contrary to the collisionless Landau damping) at the apparent absence of collisional terms in kinetic equation and determines very small collisional damping of the wave and of the electric field in plasma at 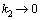 when taking into account the real-life small collision additives to the kinetic equation in the form determined by the balance energy parameter
when taking into account the real-life small collision additives to the kinetic equation in the form determined by the balance energy parameter 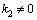 .Integral (17) is calculated in the principal value sense that corresponds to the form of the integral (7) obtained using complex variables.It is inconceivable that there would not be arbitrarily small wave damping in the presence of arbitrarily small but non-zero terms of collisional kinetic equation.Thus, it is clear that we obtain by (16) or (17) at
.Integral (17) is calculated in the principal value sense that corresponds to the form of the integral (7) obtained using complex variables.It is inconceivable that there would not be arbitrarily small wave damping in the presence of arbitrarily small but non-zero terms of collisional kinetic equation.Thus, it is clear that we obtain by (16) or (17) at 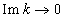 not-damping collisionless Vlasov solution [1] with the integral in the principal value sense, hence proposed by Landau [2] eight years later adding to the complex Vlasov dispersion equation the imaginary residue at the pole
not-damping collisionless Vlasov solution [1] with the integral in the principal value sense, hence proposed by Landau [2] eight years later adding to the complex Vlasov dispersion equation the imaginary residue at the pole 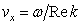 leading to the so-called Landau damping is erroneous. The real problem is to find the roots of a complex dispersion equation without any artificial additives.Due to the smallness of the range
leading to the so-called Landau damping is erroneous. The real problem is to find the roots of a complex dispersion equation without any artificial additives.Due to the smallness of the range 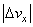 near the singularity point
near the singularity point 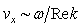 and smallness
and smallness 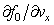 at large
at large 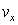 , corrections due to the missing collision term in the kinetic equation influence usually very weakly on the solution of the dispersion equations (16), (17), however obtaining solution for
, corrections due to the missing collision term in the kinetic equation influence usually very weakly on the solution of the dispersion equations (16), (17), however obtaining solution for 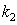 requires to attract additional new equation (since the dispersion equation contains at least two parameters
requires to attract additional new equation (since the dispersion equation contains at least two parameters 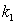 and
and 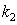 to be determined) which takes into account the energy loss in collisions of electrons with each other and with atoms and molecules present in plasma.In computing, for example, the modulated flux of electrons entrained by non-damping Van Kampen waves at
to be determined) which takes into account the energy loss in collisions of electrons with each other and with atoms and molecules present in plasma.In computing, for example, the modulated flux of electrons entrained by non-damping Van Kampen waves at 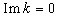 it is necessary to carry out a smooth cutoff of the distribution function
it is necessary to carry out a smooth cutoff of the distribution function 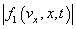 near the critical point
near the critical point 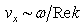 in accordance with the condition (14). Integral energy balance can be written, for example, as relation of the type
in accordance with the condition (14). Integral energy balance can be written, for example, as relation of the type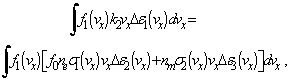
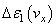 is energy loss per electron associated with a decrease in the number of electrons with an additional wave propagation velocity
is energy loss per electron associated with a decrease in the number of electrons with an additional wave propagation velocity 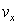 ;
; 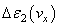 ,
, 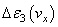 are portions of transmitted energy;
are portions of transmitted energy; 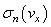 are collision cross sections;
are collision cross sections; 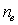 is electron density;
is electron density; 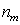 is density of atoms and molecules. In this
is density of atoms and molecules. In this 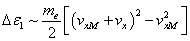
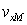 is proper velocity of electron along the axis
is proper velocity of electron along the axis 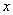 in Maxwell distribution
in Maxwell distribution 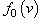 independent on the wave speed. In expression (19) one can add also any other energy-exchange processes.It is assumed that at extreme complexity of calculations using original kinetic equation, the proposed approximations with averaging
independent on the wave speed. In expression (19) one can add also any other energy-exchange processes.It is assumed that at extreme complexity of calculations using original kinetic equation, the proposed approximations with averaging 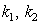 and calculation averaged
and calculation averaged 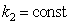 based on the energy balance represent the main features of the damping plasma waves. A more detailed exposition is presented in [3], where are marked some obvious logical contradictions that arise when using Landau rules: violation of the energy conservation law in the damping waves; the appearance of exponentially divergent solution at
based on the energy balance represent the main features of the damping plasma waves. A more detailed exposition is presented in [3], where are marked some obvious logical contradictions that arise when using Landau rules: violation of the energy conservation law in the damping waves; the appearance of exponentially divergent solution at 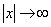 ; uncertainties in calculating the residue or the half residue near/on the real axis of the wave velocity
; uncertainties in calculating the residue or the half residue near/on the real axis of the wave velocity 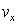 ; jump transition between the non-zero values of the damping parameter
; jump transition between the non-zero values of the damping parameter 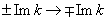 when choosing the bypass direction around the pole (cf. inspiring causality principle in [4]) or at infinitesimal displacement of the pole across the real axis
when choosing the bypass direction around the pole (cf. inspiring causality principle in [4]) or at infinitesimal displacement of the pole across the real axis 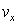 ; contradictions of the calculating residue or half residue at the pole.
; contradictions of the calculating residue or half residue at the pole.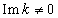 determined by collision term in the kinetic equation, with the substantiation of impossibility of collisionless Landau damping, which leads to a number of obvious logical contradictions [3]. Thereby: 1. Using technology of complex variables to solve the equations for waves
determined by collision term in the kinetic equation, with the substantiation of impossibility of collisionless Landau damping, which leads to a number of obvious logical contradictions [3]. Thereby: 1. Using technology of complex variables to solve the equations for waves 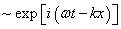 with complex
with complex 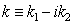 ,
, 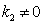 leads to results that are not equivalent to the solution of equations with real physical variables and waves Nonlinear complex expressions lead to errors in the transition to the real relations of physically observable real quantities with violation energy conservation law.2. Smoothed transition to the singularity point
leads to results that are not equivalent to the solution of equations with real physical variables and waves Nonlinear complex expressions lead to errors in the transition to the real relations of physically observable real quantities with violation energy conservation law.2. Smoothed transition to the singularity point 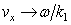 in which the real integrand of the real dispersion integral remains finite for any values
in which the real integrand of the real dispersion integral remains finite for any values 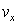 arbitrarily close to
arbitrarily close to 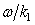 leads to the dispersion integral in the principal value sense without the need to supplement it with imaginary residue at the singularity point.3. Moreover, the requirement of positivity of the total distribution function (14) leads to the necessity of its cutting off near the singularity point with resulting the finite integrand and the finite dispersion integral.4. When adding collision terms into the kinetic equation, surprisingly simple and natural averaging of the real dispersion equation over the period of oscillations leads to the dispersion equation for the two unknown parameters
leads to the dispersion integral in the principal value sense without the need to supplement it with imaginary residue at the singularity point.3. Moreover, the requirement of positivity of the total distribution function (14) leads to the necessity of its cutting off near the singularity point with resulting the finite integrand and the finite dispersion integral.4. When adding collision terms into the kinetic equation, surprisingly simple and natural averaging of the real dispersion equation over the period of oscillations leads to the dispersion equation for the two unknown parameters 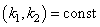 .5. The second equation (19) to determine the values
.5. The second equation (19) to determine the values 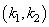 is averaged over the period
is averaged over the period 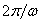 energy balance equation, and the exponential damping of the wave at arbitrarily infinitesimal collision term can lead to arbitrarily infinitesimal value
energy balance equation, and the exponential damping of the wave at arbitrarily infinitesimal collision term can lead to arbitrarily infinitesimal value 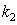 .6. In the case of the collisionless plasma such averaging in (11) is not possible, and the solution of the dispersion equation (11) with
.6. In the case of the collisionless plasma such averaging in (11) is not possible, and the solution of the dispersion equation (11) with 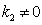 and exponentially damping wave with
and exponentially damping wave with 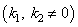 does not exist.Thus, the main results are: (1) nonphysical negative electron distribution functions must be cut off, what leads to elimination of singular points in the dispersion equation; (2) the use of complex expressions for the wave functions with solving nonlinear complex dispersion equation leads to erroneous relations between physically observable real wave parameters and the emergence of collisionless damping; (3) solving the real wave dispersion equation with constant parameters
does not exist.Thus, the main results are: (1) nonphysical negative electron distribution functions must be cut off, what leads to elimination of singular points in the dispersion equation; (2) the use of complex expressions for the wave functions with solving nonlinear complex dispersion equation leads to erroneous relations between physically observable real wave parameters and the emergence of collisionless damping; (3) solving the real wave dispersion equation with constant parameters 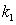 and
and 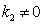 (at constant real
(at constant real 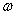 ) is possible only when averaged over the period oscillation values
) is possible only when averaged over the period oscillation values 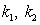 . At the same time their determination requires the addition of the second equation with
. At the same time their determination requires the addition of the second equation with 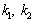 , which may be an energy balance equation when adding collisional terms in kinetic equation.Carried out in this paper relatively very simple analysis leads to the conclusion that an analytical description of the damping/growing electron waves in plasma is impossible without adding appropriate collision (energy-exchange) terms in the collisionless kinetic equation.The principal result of this paper is demonstration of the serious consequences of commonly used in physics of wave processes in weak collisional plasma the techniques in the form of mathematically correct transformations of nonlinear complex expressions that leads to completely erroneous conclusions about the true relations of real physical observables. In particular, values
, which may be an energy balance equation when adding collisional terms in kinetic equation.Carried out in this paper relatively very simple analysis leads to the conclusion that an analytical description of the damping/growing electron waves in plasma is impossible without adding appropriate collision (energy-exchange) terms in the collisionless kinetic equation.The principal result of this paper is demonstration of the serious consequences of commonly used in physics of wave processes in weak collisional plasma the techniques in the form of mathematically correct transformations of nonlinear complex expressions that leads to completely erroneous conclusions about the true relations of real physical observables. In particular, values 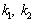 in Eq. (11) depend on
in Eq. (11) depend on 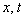 unlike equations (7), (9).These results are correction of the author's comment pp. 515 - 516 to the Russian translation of [5]. Trivial explanation of many-years ambiguities of Vlasov-Landau wave damping in weakly collisional plasma by uncritical using results of transformations the complex nonlinear equations is shocking. There is the open question: whether now Landau damping is considered and can be considered as an outstanding discovery of plasma physics?
unlike equations (7), (9).These results are correction of the author's comment pp. 515 - 516 to the Russian translation of [5]. Trivial explanation of many-years ambiguities of Vlasov-Landau wave damping in weakly collisional plasma by uncritical using results of transformations the complex nonlinear equations is shocking. There is the open question: whether now Landau damping is considered and can be considered as an outstanding discovery of plasma physics? Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML