| [1] | A. Bensoussan, J.-L. Lions, G. Papanicolaou, Asymptotic Analysis of Periodic Structures. 1978, North Holland. |
| [2] | F. Léné, Contribution à l'étude des matériaux composites et de leur endommagement. Thèse de Doctorat d'Etat, Université Pierre et Marie Curie, Paris 1984. |
| [3] | F. Léné, and D. Leguillon, 1982, Homogenized constitutive law for a partially cohesive composite material. International Journal of Solids and Structures, 18, 443-458. |
| [4] | M.Z. Asik, S. Tezacan, 2005, A mathematical model for the behavior of laminated glass beams. Comp. Struct., 83, 1742-1753. |
| [5] | M.G. Kulkarni, P.H. Geubelle, K. Matous, 2009, Multi-scale modeling of heterogeneous adhesives: Effect of particle decohesion. Mechanics of Materials, 41, 573-583. |
| [6] | A. Brillard, M. El Jarroudi, 2001, Asymptotic behaviour of a cylindrical elastic structure periodically reinforced along identical fibres. IMA J. Appl. Math. 66, 567-590. |
| [7] | G. Chatzigeorgiou, N. Charalambakis, F. Murat, 2008, Homogenization problems of a hollow cylinder made of elastic materials with discontinuous properties. International Journal of Solids and Structures, 45, 5165-5180. |
| [8] | V. Kushch, S. Shmegera, L. Mishmaevsky~Jr., 2011, Elastic interaction of partially debond circular inclusions. Application to fibrous composite. International Journal of Solids and structures, 48, 2413-2421. |
| [9] | J.-C. Michel, H. Moulinec, P. Suquet, 1999, Effective properties of composite materials with periodic microstructure: a computational approach. Comput. Meth. Appl. Mech. Eng., 172, 109-143. |
| [10] | P. Gruber, 2008, FETI-based Homogeneization of composites with perfect bonding and debonding of constituents. Bulletin of Applied Mechanics, 4, 11-17. |
| [11] | M. Serpilli, S. Lenci, 2012, Asymptotic modelling of the linear dynamics of laminated beams. International Journal of Solids and Structures 49, 1147-1157. |
| [12] | A. Sili, 2003, Homogenization of an elastic medium reinforced by anisotropic fibers. C. R. Mecanique 331, 655-660. |
| [13] | YH Zhao, GJ Weng, 2002, The effect of debonding angle on the reduction of effective modull of particule and fiber-reinforced composites. J. Appl. Mech., 69, 292-302. |
| [14] | Z. Dostal, D. Horak, O. Vlach, 2007, FETI-based algorithms for modelling of fibrous composite materials with debonding. Mathematics and Computers in Simulation, 76, 57-64. |
| [15] | H. Teng, 2010, Stiffness properties of particulate composites containing debonded particules. International Journal of Solids and Structures, 47, 2191-2200. |
| [16] | F. Greco, 2009, Homogeneized mechanical behaviour of composite micro-structures including micro-cracking and contact evolution. Engineering Fracture Mechanics, 76, 182-208. |
| [17] | A. Caporale, R. Luciano, E. Sacco, 2006, Micromechanical analysis of interfacial debonding in unidirectional fiber-reinforced composites. Comput. Struct., 84, 2200-2211. |
| [18] | H. Teng, Transverse stiffness properties of unidirectional fiber composites containing debonded fibers. Composites: part A. 38, 682-690. |
| [19] | K. Matous, P. Geubelle, 2006, Multiscale modelling of particle debonding in reinforced elastomers subjected to finite deformations. Int. J. Numer. Meth. Engng, 65, 190-223. |
| [20] | Y. Berrehili, J.-J. Marigo, 2013, The homogenized behavior of unidirectional fiber-reinforced composite materials in the case of debonded fibers. Mathematics and Mechanics of Complex Systems, sous presse. |
| [21] | Y. Berrehili, 2014, The effective behavior of laminated composite materials in the case of debonded folds, International Journal of Composite Materials, vol. 4, No. 2. |
| [22] | M. David, J.-J. Marigo, C. Pideri, 2012, Homogenized Interface Model Describing Inhomogeneities Localized on a Surface. J. Elasticity, 109, 153-187. |
| [23] | J.-J. Marigo, C. Pideri, 2011, The effective behavior of elastic bodies containing microcracks or microholes localized on a surface. International Journal of Damage Mechanics, 20, 1151-1177. |
| [24] | Y. Berrehili, J.-J. Marigo, 2010, Modélisation en 2D du comportement d'un composite fibré à constituants décollés. Physical and Chemical News, 53, 10-14. |
| [25] | Y. Berrehili, 2014, Bending of a Fiber-Reinforced Composite Beam with Debonded Fibers, International Journal of Composite Materials, vol. 4, No. 2. |
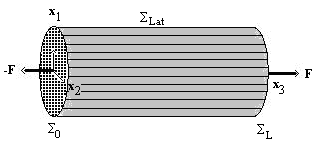
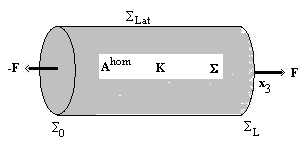
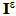 (ε is the period of the microstructure destined to tend to zero [22, 23]).Working in the framework of linear elasticity, the problem consists in seeking for the displacement and the associated stress fields, denoted respectively by
(ε is the period of the microstructure destined to tend to zero [22, 23]).Working in the framework of linear elasticity, the problem consists in seeking for the displacement and the associated stress fields, denoted respectively by 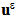 and
and 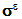 so that the dependence in ε be explicit, solutions to the following traction problem:
so that the dependence in ε be explicit, solutions to the following traction problem: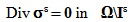
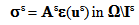
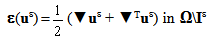
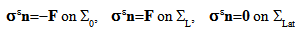
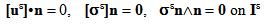
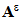 denote the elasticity tensor of the composite beam, ε (
denote the elasticity tensor of the composite beam, ε (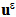 ) the strain field associated with the displacement field
) the strain field associated with the displacement field 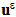 , n the outer normal of ∑0(n=-e3), ∑L(n=e3) or ∑Lat(n=n1e1+ n2e2 with n12+n22=1) and [
, n the outer normal of ∑0(n=-e3), ∑L(n=e3) or ∑Lat(n=n1e1+ n2e2 with n12+n22=1) and [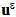 ] the jump of the displacement field
] the jump of the displacement field 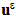 across the interface
across the interface 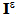 . The three relations of the last line reflect the continuity of normal displacement field, the continuity of the stress vector and the nullity of the shear on the debonded interfaces
. The three relations of the last line reflect the continuity of normal displacement field, the continuity of the stress vector and the nullity of the shear on the debonded interfaces 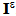 (see [10, 13, 17] for other interface conditions).
(see [10, 13, 17] for other interface conditions).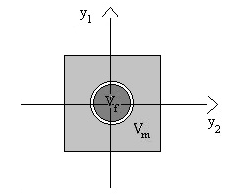
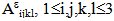 , are given therefore by[2]:
, are given therefore by[2]: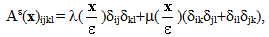
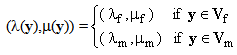
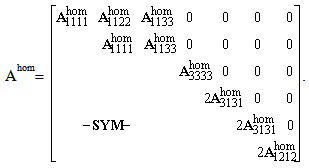
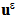 can be expanded as follows:
can be expanded as follows: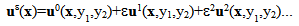
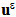 (x) can be written as in [20]:
(x) can be written as in [20]: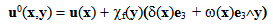
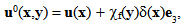
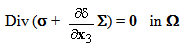
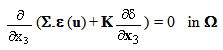
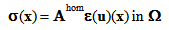
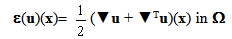
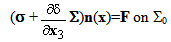
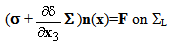
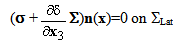
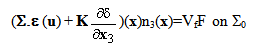
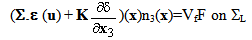
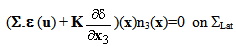
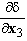 represents the normal effort). We see that, in the first equation, the term
represents the normal effort). We see that, in the first equation, the term 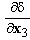 ∑ plays the role of a pre-stressed field whereas in the second one, the term ∑ε(u) plays the role of a pre-tensioning field of the beam composite. This system of equations is completed by the boundary conditions (15)-(20).
∑ plays the role of a pre-stressed field whereas in the second one, the term ∑ε(u) plays the role of a pre-tensioning field of the beam composite. This system of equations is completed by the boundary conditions (15)-(20).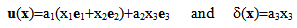
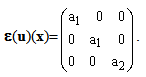
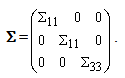
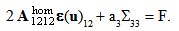
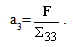
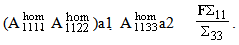
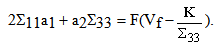
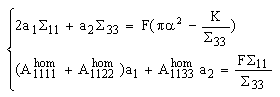
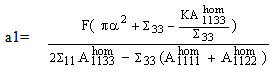
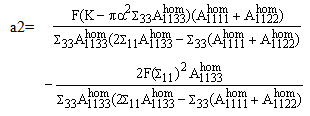
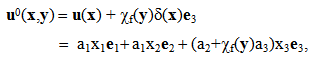
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML