-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2014; 4(2): 29-52
doi:10.5923/j.ijtmp.20140402.02
On Achievements, Shortcomings and Errors of Einstein
C. Y. Lo
Applied and Pure Research Institute, 15 Walnut Hill Rd., Amherst, NH 03031
Correspondence to: C. Y. Lo , Applied and Pure Research Institute, 15 Walnut Hill Rd., Amherst, NH 03031.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The electromagnetic energy is not equivalent to mass. Thus, E = mc2 is not generally valid. Experimentally, a piece of heated-up metal has reduced weight instead of increased as predicted by E = mc2. Moreover, for an electromagnetic wave to have a gravitational solution, the photonic energy-momentum tensor with an anti-gravity coupling must be added to the Einstein field equation. To have a dynamic solution for massive sources, the Einstein equation must be modified to the Lorentz-Levi-Einstein equation, which additionally has the gravitational energy-stress tensor with the anti-gravity coupling because the Einstein equation has no bounded dynamic solution as Gullstrand suspected. Moreover, the linearized equation is actually a linearization of the Lorentz-Levi-Einstein equation. Thus, the space-time singularity theorems of Penrose & Hawking are irrelevant to physics because its implicit assumption of unique sign for all couplings is invalid. The positive mass theorem of Yau & Schoen (and Witten) is misleading in physics because of the same invalid assumption. Thus, the Fields Medal has been wrong at least twice. Also, the 2011 Shaw Prize to Christodoulou actually awards his errors against the honorable Gullstrand. Due to the absence of the radiation reaction force, general relativity is incomplete. The static charge-mass interaction necessarily implies Einstein’s unification between gravitation and electromagnetism. This repulsive interaction would explain the weight reduction of charged capacitors and the Space-Probe Pioneer Anomaly. The repulsive force breaks the basis for black holes, that gravity is always attractive. However, such force was overlooked for 80 years due to believing in E = mc2 as unconditionally true. In conclusion, Einstein’s general relativity is incomplete and needs rectifications. Additional difficulties were due to the confusion created by the Wheeler School and the misleading results of Yau & Schoen and Witten. However, the main source of errors is that Einstein’s claim on the existence of dynamic solutions for his equation is invalid.
Keywords: Dynamic solution, Gravitational radiation, Anti-gravity coupling, Principle of causality
Cite this paper: C. Y. Lo , On Achievements, Shortcomings and Errors of Einstein, International Journal of Theoretical and Mathematical Physics, Vol. 4 No. 2, 2014, pp. 29-44. doi: 10.5923/j.ijtmp.20140402.02.
Article Outline
- “Unthinking respect for authority is the greatest enemy of truth.” – A. Einstein
1. Introduction
- Einstein is commonly recognized as a genius because he created new theories and led us with accurate predictions to new areas of physics, namely, special relativity, quantum mechanics and general relativity. In special relativity, he revolutionized the notion of space-time and established a formula between energy and mass E = mc2.1) The notion of photon plays a central role in quantum mechanics. In general relativity, he amazed us by his three accurate predictions. Thus, a faith in Einstein was developed. In particular, many believed that the Einstein equation is correct.However, as time has gone by the shortcomings of his theories are gradually shown and even include mistakes. We admire Einstein not because he was perfect as we previously believed, but rather for his ingenuity in starting new chapters of physics. In what follows, we shall point out the current problems. This leads to the necessary rectification of his theories, in particular, the Einstein equation. 2) Then, it also becomes clear that his conjecture of unification between gravitation and electromagnetism is established. Nevertheless because of the blind faith to Einstein and inadequacy in mathematics, many theorists erroneously claimed to have explicit dynamic solutions.3) Apparently, such claims were mistaken by some mathematicians as the truth because they do not understanding the related physics. Thus, the subsequent works done by those mathematicians are misleading in physics. 4) These have led to the difficulty to prove Einstein’s conjecture of unification. Thus, such errors must be pointed out to remove the obstacles to progress in general relativity. Finally, Einstein’s conjecture of unification turns out to be correct at the end. It is up to us to further explore what he has started and perform further investigations.
2. Special Relativity and the Formula E = mc2
- While special relativity has the least problems, the unconditional validity of the formula E = mc2 is only a speculation that has never been verified [1]. In fact, Einstein had tried very hard for years (1905-1909) to prove this formula to be generally valid, but failed [2]. The formula can be traced back to special relativity, which suggested a rest inertial mass m0 has the rest energy of m0c2. This is supported by the nuclear fissions with ΔE = Δmc2, where Δm is the mass difference after the fission and ΔE the total energy created and is usually a combination of different types of energy.1) However, for an arbitrary energy E, the relation m = E/c2 is not only an unverified speculation, but also an obstacle for progress in physics [1]. According to general relativity, such a claim is incorrect for electromagnetic energy. The Einstein field equation is,
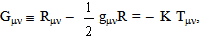 | (1) |
3. The Question of Photons
- When Einstein proposed the notion of photon, it consists of a quantum of electromagnetic energy, and it acts like a particle in the photo–electric effect. It has been observed that the particle π0 meson decays into two photons (i.e., π0 → γ + γ). This was mistakenly considered as evidence that the electromagnetic energy is equivalent to mass. However, there would be a conflict if a photon includes only electromagnetic energy since the electromagnetic energy-stress tensor is traceless. Therefore, the photons must consist of non-electromagnetic energy. Since a charged particle has mass, it is natural that the non-electromagnetic energy is the gravitational energy. When Einstein proposed the notion of photon, he had not conceived general relativity yet. Moreover, since Hawking and Penrose claimed that general relativity was not applicable in microscopic scale, the possibility of including gravitational energy in photons was ignored. It will be shown that Hawking and Penrose are incorrect (see sections 4 & 5). Moreover, it has been shown that the energy of photons is, indeed, the sum of the energies of the electromagnetic wave component and that of the gravitational wave component [6]. In other words, the energy-stress of photons T(L)ab is
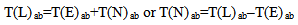 | (2) |
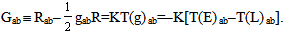 | (3) |
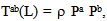 | (4) |
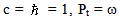 is the energy. If the photons are a bundle of massless particles, the photonic energy tensor has been obtained [8] as follows:
is the energy. If the photons are a bundle of massless particles, the photonic energy tensor has been obtained [8] as follows: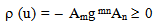 | (5) |
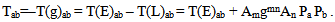 | (6) |
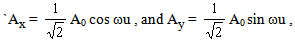 | (7) |
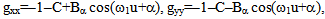 | (8) |
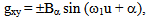 where C and Bα are small constants, and ω1 = 2ω. Thus, metric (8) is a circularly polarized wave with the same direction of polarization as the electromagnetic wave (7). On the other hand, one also has
where C and Bα are small constants, and ω1 = 2ω. Thus, metric (8) is a circularly polarized wave with the same direction of polarization as the electromagnetic wave (7). On the other hand, one also has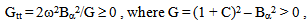 | (9) |
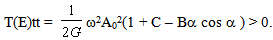 Then eq. (4), eq. (5) and eq. (6) give
Then eq. (4), eq. (5) and eq. (6) give 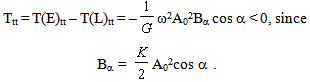 | (10) |
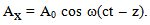 | (11) |
4. Problems and Errors in General Relativity
- In general relativity, the most important statement of Einstein is the existence of a bounded dynamic solution for the Einstein equation. On this issue, Einstein and Gullstrand [9], the chairman (1922-1929) of the Nobel Committee for Physics are in opposition to each other. To clarify the issue, one must be clear on some obscure errors. It was generally believed that the linearized Einstein equation would give a first order approximation of the solution for the Einstein equation [10]. For space-time metric gμν , the Einstein equation of 1915 is
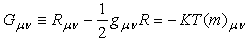 | (12) |
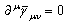 is
is 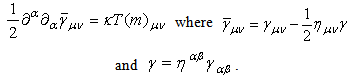 | (13) |
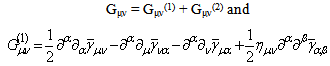 | (14) |
4.1. Examples of no Bounded Dynamic Solutions
- Many believed that it would be very difficult to show that there is no dynamic solution for the Einstein equation. However, if one would look carefully, it is possible to have very remarkable evidence such as the two examples.a) The metric obtained by Bondi, Pirani, & Robinson [14] The metric is as follows:
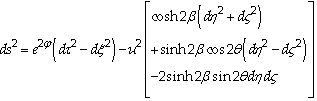 | (15a) |
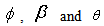 are functions of
are functions of It satisfies the differential equation (i.e., their Eq. 2.8),
It satisfies the differential equation (i.e., their Eq. 2.8),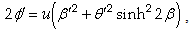 | (15b) |
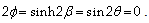 These reduce (15a) to
These reduce (15a) to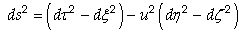 | (15c) |
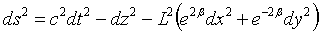 | (16) |
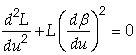 | (17) |
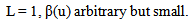 | (18) |
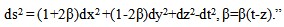 | (19) |
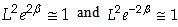 | (20a) |
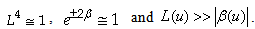 | (20b) |
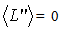 | (21) |
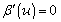 in the whole interval of u. Also, from eq. (20), one would obtain L (≅ 1) > 0, and one has 0 > L’’(u) if β’(u) 0. Thus, – L’(u) is a monotonic increasing function in any finite interval of u since β’(u) = 0 means L’’ = 0, i.e., no wave. In turn, since β’(u) is a “wave factor”, this implies that L(u) is an unbounded function of u. Therefore, this would contradict the requirement that L is bounded. In other words, eq. (17) does not have a bounded wave solution. Moreover, the second order term L’’ would give a very large term to L, after integration. Also, linearizing eq. (17) to L” = 0 leads to no wave. Now, let us investigate the errors of Misner et al. [15; p. 958]. They assumed that the signal β(u) has duration of 2T. For simplicity, it is assumed that definitely
in the whole interval of u. Also, from eq. (20), one would obtain L (≅ 1) > 0, and one has 0 > L’’(u) if β’(u) 0. Thus, – L’(u) is a monotonic increasing function in any finite interval of u since β’(u) = 0 means L’’ = 0, i.e., no wave. In turn, since β’(u) is a “wave factor”, this implies that L(u) is an unbounded function of u. Therefore, this would contradict the requirement that L is bounded. In other words, eq. (17) does not have a bounded wave solution. Moreover, the second order term L’’ would give a very large term to L, after integration. Also, linearizing eq. (17) to L” = 0 leads to no wave. Now, let us investigate the errors of Misner et al. [15; p. 958]. They assumed that the signal β(u) has duration of 2T. For simplicity, it is assumed that definitely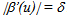 in the period 2T. Before the arrival of the signal at u = x, one has
in the period 2T. Before the arrival of the signal at u = x, one has 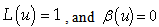 | (22) |
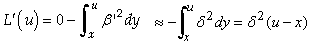 for
for 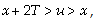
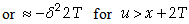 | (23) |
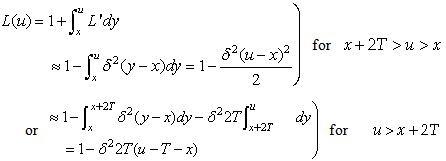 | (24) |
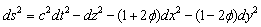 | (25) |
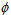 is a bounded function of u (= ct – z). Note that metric (25) is the linearization of metric (16) if
is a bounded function of u (= ct – z). Note that metric (25) is the linearization of metric (16) if 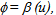 but it cannot be obtained through the non-linear Einstein equation. Thus, the problem of waves illustrates that the linearization is not valid for the dynamic case when gravitational waves are involved since eq. (17) does not have a bounded wave solution. In other words, the Einstein equation and its linearization are essentially independent equations.
but it cannot be obtained through the non-linear Einstein equation. Thus, the problem of waves illustrates that the linearization is not valid for the dynamic case when gravitational waves are involved since eq. (17) does not have a bounded wave solution. In other words, the Einstein equation and its linearization are essentially independent equations. 4.2. Other Errors in the Non-existence of a Dyanmic Solution
- Since the error of the non-existence of dynamic solution was made by Einstein, other theorists also made errors by having unverified faith on Einstein. Wald [5] is the better known among them.According to Einstein [10], in general relativity weak sources would produce a weak field, i.e.,
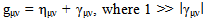 | (26) |
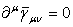 is eq. (13). Then, the linearized vacuum Einstein equation means
is eq. (13). Then, the linearized vacuum Einstein equation means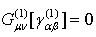 | (27) |
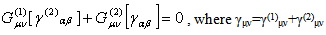 | (28) |
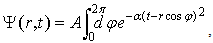 | (29) |
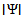 is everywhere bounded. Then, ‘t Hooft [22, 23] claimed that his solution, Ψ is obtained by superimposing plane wave packets of the form
is everywhere bounded. Then, ‘t Hooft [22, 23] claimed that his solution, Ψ is obtained by superimposing plane wave packets of the form 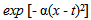 rotating them along the z axis over angle φ, so as to obtain a cylindrical solution. Note that since the integrand
rotating them along the z axis over angle φ, so as to obtain a cylindrical solution. Note that since the integrand 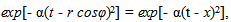 there is no rotation along the z axis. The function
there is no rotation along the z axis. The function 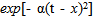 is propagating from
is propagating from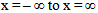 as time t increases.Note, however, that in a superimposition the integration is over a parameter of frequency ω unrelated to the x-axis; whereas the solution (29) is integrated over φ(x, y). Since, (29) is a combination that involves the coordinate φ (x, y), it is not a superimposition of plane waves propagating along the x-axis. Furthermore, the integration over all angles φ is a problem that would violate the requirement of the idealization because it requires that the plane wave is valid over the whole x-y plane. Thus, function (29) is not valid as an idealization in physics.Therefore, in solution (29), two errors have been made, namely: 1) the plane wave has been implicitly extended beyond its physical validity, and 2) the integration over dφ is a process without a valid physical justification. Moreover, it has been shown that there are no valid sources that can be related to solution (29) [23]. Thus, since the principle of causality is also violated, his solution is not valid in physics.
as time t increases.Note, however, that in a superimposition the integration is over a parameter of frequency ω unrelated to the x-axis; whereas the solution (29) is integrated over φ(x, y). Since, (29) is a combination that involves the coordinate φ (x, y), it is not a superimposition of plane waves propagating along the x-axis. Furthermore, the integration over all angles φ is a problem that would violate the requirement of the idealization because it requires that the plane wave is valid over the whole x-y plane. Thus, function (29) is not valid as an idealization in physics.Therefore, in solution (29), two errors have been made, namely: 1) the plane wave has been implicitly extended beyond its physical validity, and 2) the integration over dφ is a process without a valid physical justification. Moreover, it has been shown that there are no valid sources that can be related to solution (29) [23]. Thus, since the principle of causality is also violated, his solution is not valid in physics.5. The Dynamic Case for the Einstein Equation with Massive Sources
- Einstein started his faith on his theory of general relativity with the remarkable calculation of the remaining perihelion of Mercury. However, Gullstrand suspected that his calculation is questionable since he failed to show such a calculation is derivable from a many-body problem approach. This is a very insightful criticism. Thus, Einstein was awarded a Nobel Prize for his photo-electric effects, and a controversy accompanies the theory since then. In 1995, it is proven that for the dynamic case, i.e., when the gravitational waves are involved, there is no bounded dynamic solution for the Einstein equation. In other words, Einstein has been proven wrong, but Gullstrand is right. However, because the proof is rather long, many theorists just do not have the time to go over it. Besides, well-known theorists such Misner et al and Wald insisted as Einstein claimed the existence of the dynamic solutions. In this paper, we show through the theories of Misner et al. [15] and Wald [5] and examples in the literature that they are mistaken. The main error is that they believe that the Einstein equation has bounded dynamic solutions and thus is valid for the dynamic case. However, it has been shown that there is no dynamic solution for the Einstein equation. In short, the Einstein equation is valid only for the static and stable cases, but invalid for the dynamic case.
5.1. The Question of a Correct Field Equation for Massive Sources
- An obvious question is what is the correct field equation for the dynamic case? Moreover, how such an equation would be related to the “linearized” equation, which is supported by observation. A meaningful answer would be that the “linearized” equation is obtained though a valid mathematical linearization of the correct field equation. Moreover, since the “linearized” equation with massive sources is supported by observation, there must be a way to justify its validity independently. This leads to the Maxwell-Newton Approximation [11-13].
 | (13a) |
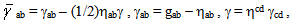 and ηab is the flat metric. A solution of eq. (13a) is
and ηab is the flat metric. A solution of eq. (13a) is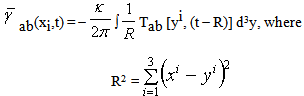 | (13b) |
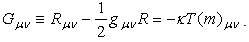 | (12) |
5.2. The Weak Gravity of Massive Matter and Einstein Equation of the 1995 Update
- It will be shown that eq. (13a) can be derived from Einstein’s equivalence principle. Based on this, the equation of motion for a neutral particle is the geodesic equation. In comparison with Newton's second law, one obtains that the Newtonian potential of gravity is approximately c2gtt/2. Then, in accord with the Poisson equation and special relativity, the most general equation for the first order approximation of gab is,
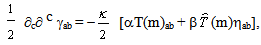 | (30a) |
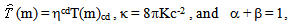 | (30b) |
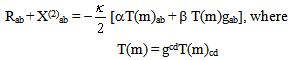 | (31a) |
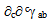 . This requires that the sum
. This requires that the sum 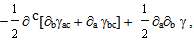 | (31b) |
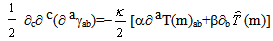 | (32a) |
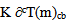 is of second order but
is of second order but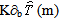 is not. However, one may obtain a second order term by a suitable linear combination of ∇cγcb and ∂bγ. From (32a), one has
is not. However, one may obtain a second order term by a suitable linear combination of ∇cγcb and ∂bγ. From (32a), one has 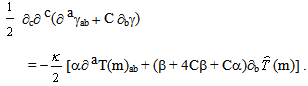 | (32b) |
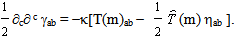 | (33) |
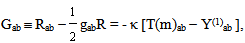 | (34) |
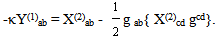 The conservation law ∇cT(m)cb = 0 and ∇cGcb ≡ 0 implies also ∇aY(1)ab = 0. If Y(1)ab is identified as the gravitational energy tensor of t(g)ab, Einstein equation of the 1995 update 11 is reaffirmed. Note that eq. (13a) is the first order approximation of eq. (34). Note, also that t(g)ab must be a tensor [11] because the radiation energy cannot be zero. A crucial discovery is that for the existence of dynamic solutions there must be different signs for the couplings [11]. (Thus, as in the case of eq. (3), the energy conditions in the space-time singularity theorems of Hawking and Penrose [5] also failed for the above case.) For the dynamic case, a modified Einstein equation [11-13] is,
The conservation law ∇cT(m)cb = 0 and ∇cGcb ≡ 0 implies also ∇aY(1)ab = 0. If Y(1)ab is identified as the gravitational energy tensor of t(g)ab, Einstein equation of the 1995 update 11 is reaffirmed. Note that eq. (13a) is the first order approximation of eq. (34). Note, also that t(g)ab must be a tensor [11] because the radiation energy cannot be zero. A crucial discovery is that for the existence of dynamic solutions there must be different signs for the couplings [11]. (Thus, as in the case of eq. (3), the energy conditions in the space-time singularity theorems of Hawking and Penrose [5] also failed for the above case.) For the dynamic case, a modified Einstein equation [11-13] is,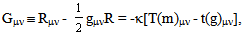 | (35) |
5.3. Implications of the Modified Einstein Equation
- The equation (35) explains why the nonlinear Einstein equation always results in violating the principle of causality because t(g)μν is neglected. Moreover, since the popular notion of black holes is a speculation based on the Einstein equation, which is not valid for the dynamic case, this notion must be thoroughly reviewed. From (35), the equation in vacuum is
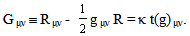 | (36) |
6. Problems in Mathematics due to a Failure in Understanding the Physics
- In mathematics, a theorem need not be simply right or wrong, but misleading because some invalid implicit assumptions. Such misleading theorems could be very damaging because of its superficial validity in mathematics. In fact, such an error can be made by top mathematicians such as M. Atiyah. Thus, such misleading results were cited as a main reason to award the 1982 and the 1990 Fields Medal to Yau and Witten, and to award the 2011 Shaw Prize in mathematics to Christodoulou. 9)Briefly, the positive mass conjecture [33, 34] says that if a three-dimensional manifold has positive scalar curvature and is asymptotically flat, then the mass in the asymptotic expansion of the metric is positive (Wikipedia). The unique coupling signs are also implicitly used in the positive energy theorem of Schoen and Yau [33, 35]. A crucial assumption in the theorem is that the solution is asymptotically flat. Yau [33] requires the metric,
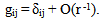 | (37) |
7. Unification of Gravitation and Electromagnetism
- Now, let us consider the case that electromagnetism is involved. Since the photons include gravitational energy, the unification of gravitation and electromagnetism is necessary. In general relativity, it is clear that a charge can create a field that couples with a mass. This is shown [1] by the Reissner-Nordstrom metric [15] (with c = 1) created by a particle with charge q and mass M is as follows (see also remark 11) in Appendix A):
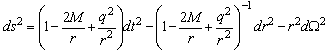 | (37) |
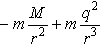 | (38) |
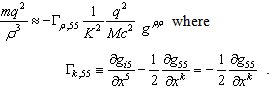 | (39) |
8. Conclusions and Discussions
- Now, since the Einstein equation has no dynamic solution, rectification of the theory is necessary. The important conclusions are: 1) E = mc2 is not generally valid. In particular, the electromagnetic energy alone is not equivalent to mass. 2) The photons include energy from its gravitational components. 3) Einstein’s general relativity is valid only for the static and stable cases. However, for the dynamic case, it remains to be rectified [36] in at least two aspects: a) The exact form of the gravitational energy-stress tensor is not known; and b) The radiation reaction force is also not known. Due to the radiation reaction force, considering general relativity as a theory of geometry is questionable. Since the full field equation is unclear, the notion of black holes should also be reviewed. Moreover, since the photons include gravitational energy, the unification of gravitation and electromagnetism is necessary. A five-dimensional theory [39] would be a candidate because it includes the charge-mass interaction with charge-square coupling. This analysis reveals also that some physicists are inadequate in understanding the mathematics and the principle of causality. 14)Also, there are positive results learned from the issue of dynamic solutions. The existence of a dynamic solution requires [11], an additional gravitational energy-momentum tensor with an antigravity coupling, i.e., the Lorentz-Levi- Einstein equation.6) Thus, the space-time singularity theorems, which require the same sign for couplings, are actually irrelevant to physics. Recall the need of modifying the Einstein equation for the gravity of the electromagnetic wave. In such a modification, the anti-gravity coupling of the photonic energy-stress tensor must also be added [8]. Otherwise there is no solution for the gravity of an electromagnetic wave. Thus, the anti-gravity coupling is important. However, string theorists, such as Witten [34] failed in understanding the necessity of such anti-gravity coupling.Using the assumption of unique coupling sign implicitly, the positive energy theorem of Schoen and Yau is misleading [35].12) For instance, without a proof, they act as if that their theorem includes the case of dynamic solutions. The tragic is that Yau [33] and Witten [34] produced a misleading result, but failed to see this as a problem. Such error should be responsible for the lack of progress in String theory. Moreover, E = mc2 is not generally valid [20], and such recognition is crucial to identify, after 80 years, the charge-mass interaction [1]. This repulsive force explains the weight reduction of charged capacitors and potentially the Space-Probe Pioneer anomaly [42]. This force is not subjected to electromagnetic screening because it is proportional to the charge square. Thus, it would be useful to detect things since the strength of such detection can be adjusted with the potential of a charged capacitor [39]. The verifications of the charge-mass interaction imply that Einstein’s unification between electromagnetism and gravitation is proven valid [39, 42]. Einstein failed to see this himself because of his two shortcomings: 1) He failed to see, as Maxwell showed, that unification is necessary to create new interactions. 2) E = mc2 was mistaken as unconditional. Although this newly discovered repulsive force can be detected from its action to a charged capacitor, such a force cannot be generated in current four-dimensional theories. Perhaps, this is why Einstein’s unification was not recognized for a long time. Hence, Einstein turns out to be the biggest winner at the end. Many theorists started their errors because of their faith to Einstein’s claim on the existence of dynamic solutions for the Einstein equation. A theoretical obstacle was the invalid speculation that E = mc2 being unconditionally true, and consequently Harvard University and the Princeton University were the sources of major errors [43,44]. It should be noted that the charge-mass interaction implies that the assumption of Galileo that the acceleration of gravity is universal for all neutral massive matter may not always be valid [45], and thus a new revolution in physics has begun.
ACKNOWLEDGMENTS
- This paper is dedicated to Prof. P. Morrison of MIT for his unfailing guidance over 15 years. The author is grateful to Prof. A. J. Coleman for pointing out some errors in general relativity, and to Prof. I. Halperin for the mathematical foundation of Einstein’s theory. The author wishes to express his appreciation to S. Holcombe for valuable suggestions. This publication is supported by Innotec Design, Inc., U.S.A. and the Chan Foundation, Hong Kong.
Appendix A: Summary of Misrepresentations and Errors in General Relativity
- For the convenience of the readers, the errors and misinterpretations in general relativity are summarized in this Appendix. The first error, suspected by Gullstrand [9], is the non-existence of dynamic solutions. However, in 2011 half of a Shaw Prize for mathematics was awarded to Christodoulou [37] for his errors against Gullstrand. This error has been well-established because it can be illustrated with examples understandable at the undergraduate level.The fundamental issues that historically relate to errors are:1) Einstein’s 1911 assumption of equivalence between acceleration and Newtonian gravity [46]: It was used to derive the correct gravitational redshifts, but the so-obtained light bending deflection disagrees with observation.2) Einstein’s equivalence principle [7]: The effects of an accelerated frame are equivalent to a uniform gravity (generated by a metric). In physics, the local metric of a particle under the influence of gravity is a local Minkowski metric [7]. This principle can be illustrated with explicit examples and is supported by experiments. Since the local metric of the earth is only a locally constant metric at one point, Einstein pointed out that the gravity cannot be transformed away by using an accelerated frame. Thus, gravity and acceleration are not generally equivalent. a) Pauli’s misinterpretation [47]: Pauli claimed that the gravity of an infinitesimal region can be transformed away; but the local metric of a particle need not be locally Minkowski. b) The misinterpretation of Misner, Thorne & Wheeler [15]: They agree with Pauli and claimed that gravity is equivalent to acceleration in a small region of the local metric. What they referred to is the Newtonian gravity (since they agree with Fock [48] and reject the principle). Moreover, they claimed that in such a small region the local metric is necessarily Minkowski (the so-called Lorentz invariance). However, their notion of Lorentz invariance is incorrect in mathematics and is not favored by the 2009 experiment of Chu et al. [49].c) Fock [48] misinterpreted that Einstein’s equivalence principle as the 1911 assumption. He shows that it is impossible to have a metric for the Newtonian gravity in general relativity; and invalidly rejected the principle. 3) Einstein’s covariance principle: Einstein extended his principle of general relativity to unrestricted mathematical covariance and called it as the “principle of covariance”. Since different gauges would lead to different physical interpretations of the coordinates [50, 51], this is in conflict with his equivalence principle which implies the local time dilation and space contractions are unique. The experiment supports Einstein’s equivalence principle.4) Einstein’s measurement of the distance [7]: Einstein adapted the notion of distance in a Riemannian space. Such an adaptation has been pointed out by Whitehead [52] as invalid in physics. Also, it is found that his justifications for his adaptation are due to invalid applications of special relativity [53]. It turns out that the correct theory of measurement [54] is just what Einstein practiced in his calculation of light bending. Then, the measurement of distance is consistent with the observed bending of a light ray [55]. Thus, it becomes clear that to regard the Hubble redshifts as due to the Doppler effects is invalid [56], as Hubble himself also disagrees. 5) The question of a physical gauge: The invalidity of the covariance principle exposed an urgent issue, i.e., to find a valid physical gauge for a given problem. Fortunately, the Maxwell-Newton approximation has been proven to be an independently valid first order approximation for gravity due to massive sources [12], so that the binary pulsar radiation experiments can be explained satisfactorily [11, 13]. Thus, Einstein’s notion of weak gravity (including gravitomagnetism and gravitational radiation [57] 15)) is valid [12, 17, 18].6) The principle of causality is implicitly used in any scientific research. In general relativity, this principle is implicitly used by Einstein in symmetry considerations [7]. However, theorists such as Penrose [58] and ‘t Hooft [22, 23] do not understand this principle adequately. The Physical Review also failed to understand the principle of causality adequately and thus mistakenly believed that the non-linear Einstein equation has wave solutions [22]. 7) Invalidity of linearization [20]: Currently, to obtain an approximation through linearizing the Einstein equation is incorrectly believed as generally valid because linearization has been successful for the static case of massive source. However, this process of linearization for the dynamic cases is invalid since the Einstein equation actually has no bounded dynamics solutions [11, 13] because the principle of causality is violated.8) Bounded dynamic solutions: The Einstein equation has no bounded dynamic solution. Thus the perihelion of Mercury is beyond the reach of Einstein as Gullstrand [9] suspected; and the calculation for the gravitational radiation of binary pulsars is actually invalid. A conclusion from this result is that all the coupling constants cannot have the same sign, and thus the physical assumption of the space-time singularity theorems [5] is invalid. 9) The sign of coupling constants being unique was accepted since E = mc2 was considered as unconditional. However, the electromagnetic energy cannot be equivalent to mass since the trace of an electromagnetic energy-stress tensor is zero. In fact, for several years, Einstein had tried and failed to prove this formula for other type of energy [2]. 10) The photons must have non-electromagnetic energy because the meson π0 decays into two photons. The immature assumption that the photons have only electromagnetic energy was proposed before general relativity. Since a charged particle is massive, it is not surprising that the photons should include also gravitational energy.11) The static Einstein equation with the source of a charged particle implies the existence of a static repulsive force between a charge and a massive particle. Moreover, such a repulsive effect has been inadvertently observed by Tsipenyuk & Andreev [59]. Verification of such a force is necessary for general relativity. Thus, unification of gravitation and electromagnetism is actually necessary. Some argued that the effective mass of such a charged particle should be (M – q2/2r) or M should include the electromagnetic energy outside the particle. However they have been proven as theoretically invalid and against observation.Note that all the errors are directly or indirectly related to distortions of Einstein’s equivalence principle. The invalid speculation of unconditional validity of E = mc2 is the source of many errors in general relativity, and thus Einstein’s general relativity is not yet complete. Its completion would be crucial to explain the Hubble redshifts and the pioneer anomaly discovered by NASA [60-63], and may even be needed to explain problem of renormalization.
Appendix B: Experimental Verification of the Mass-Charge Repulsive Force
- The repulsive force in metric (37) can be detected with a neutral mass. To see the repulsive effect, one must have
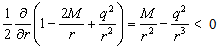 | (A1) |
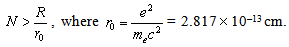 | (A2) |
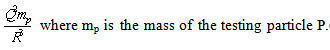 | (A3) |
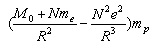 | (A4) |
Appendix C: The Current-mass Interaction
- If the electric energy leads to a repulsive force toward a mass, according to general relativity, the magnetic energy would lead to an attractive force from a current toward a mass [67, 68]. The existence of such a current-mass attractive force has been verified by Martin Tajmar and Clovis de Matos [69] from the European Space Agency. They found that a spinning ring of superconducting material increases its weight much more than expected. Thus, they believed that general relativity had been proven wrong. However, according to quantum theory, spinning super-conductors should produce a weak magnetic field. Thus, they are also measuring the interaction between an electric current and the earth, i.e. an effect of the current-mass interaction! The existence of the current-mass attractive force would solve a puzzle, i.e., why a charged capacitor exhibits the charge-mass repulsive force since a charged capacitor has no additional electric charges? In a normal situation, the charge-mass repulsive force would be cancelled by other forms of the current-mass force as Galileo, Newton and Einstein implicitly assumed. This general force is related to the static charge-mass repulsive force in a way similar to the Lorentz force is related to the Coulomb force. One may ask what is the formula for the current-mass force? However, unlike the static charge-mass repulsive force, which can be derived from general relativity; this general force would be beyond general relativity since a current-mass interaction would involve the acceleration of a charge, this force would be time-dependent and generates electromagnetic radiation. Moreover, when the radiation is involved, the radiation reaction force and the variable of the fifth dimension must be considered [41]. Thus, we are not ready to derive the current-mass interaction yet. Nevertheless, we may assume that, for a charged capacitor, the resulting force is the interaction of net macroscopic charges with the mass [4]. The irradiated ball has the extra electrons compared to a normal ball. A spinning ring of superconducting material has the electric currents that are attractive to the earth. This also explains a predicted phenomenon, which is also reported by Liu [66] that it takes time for a capacitor to recover its weight after being discharged [4]. This was observed by Liu because his rolled-up capacitors keep heat better. A discharged capacitor needs time to dissipate the heat generated by discharging, and the motion of its charges would accordingly recover to normal.
Endnotes
- 1) For a thorough discussion on the relation between the mass and the total energy of a particle, one can read the 1989 paper of L. B. Okun [70]. However, Okun did not understand that the electromagnetic energy is not equivalent to mass [1] as shown in his 2008 paper [71]. 2) Currently a major problem in general relativity is not only that Einstein’s errors are over-looked, but also that some theorists claimed as “experts” [5, 14, 15, 21, 25, 33, 34] who additionally make their own errors.3) Theorists such a Misner et al. [15], Wald [5], Christodoulou & Klainerman [21], ‘t Hooft [23], and etc. claimed to have explicit dynamic solutions. It turns out that all these are due to errors in mathematics [35, 43, 44].4) A well-known misleading result is the positive mass theorem of Schoen & Yau [33] (and the positive energy theorem of Witten [34]).5) Some considered that even the photon has mass in terms of m = E/c2, the so-called electromagnetic mass. This is due to confusing the difference between mathematics and physics. To define a mass in terms of mathematics would be misleading if it is not supported with experiments. They must show also that such an electromagnetic mass would produce the same gravitational effect as the inertial mass.6) This equation was first proposed by Lorentz [72] and later Levi-Civita [73] as a possibility in the following form,
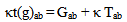 | (LL) |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML