International Journal of Theoretical and Mathematical Physics

p-ISSN: 2167-6844    e-ISSN: 2167-6852

2013;  3(5): 168-169

doi:10.5923/j.ijtmp.20130305.07

An Interpretation of Planck Constant

Harun Akkus

Department of Physics, Faculty of Science, Yuzuncu Yil University, Van, 65080, Turkey

Correspondence to: Harun Akkus , Department of Physics, Faculty of Science, Yuzuncu Yil University, Van, 65080, Turkey.

Email:

Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.

Abstract

We introduce a classical interpretation of Planck constant. We show that Planck constant corresponds to the amount of action for a standing particle which has Planck mass in the Minkowski space

Keywords: Planck Constant, Planck Mass, Planck Length, Action

Cite this paper: Harun Akkus , An Interpretation of Planck Constant, International Journal of Theoretical and Mathematical Physics, Vol. 3 No. 5, 2013, pp. 168-169. doi: 10.5923/j.ijtmp.20130305.07.

Article Outline

Maupertuis, in 1744, stated that the action for a body is the price of Nature, which should be paid to travel from one point to another in the universe. According to him, the action of body depends on its speed and on the distance it gets over [1]. In 1746, Maupertuis gave a general principle about the action of a body: when a change occurs in Nature, the quantity of action necessary for that change is as small as possible [2]. In his work, moreover, he stated that the action of a body is the product of its mass times its speed and the distance it travels. When a body is transported from one place to another in universe, its action is proportional to its mass, to its speed and to the distance over which it is transported [2], that is,
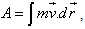(1)
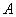where is the action, 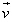is the velocity, 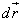is the infinitesimal radius vector (or the distance) of the body.
We can extend this definition of action to the theory of special relativity. The action for a free particle in Minkowski space can be written:
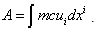(2)
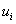Where and 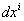are the covariant components of the 4-dimensional velocity and the contravariant components of infinitesimal four-radius vector, respectively, of the particle (or the body) in the Minkowski space and they are defined as [3]
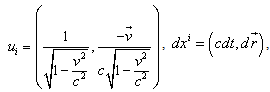(3)
where .
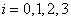Substituting the definitions in (3) in (2), we have the action,
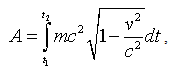(4)
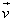where is the 3-dimensional velocity vector of the particle. In order to make that action minimum it is needed to multiply it by minus but our aim is not to make it minimum.
Now, we consider a standing particle in the inertial reference system K. The action in (4) occurs for this particle as following:
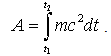(5)
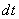The in Eq. (5) is the proper time for the standing particle. Then, the world line of this particle is a straight line which is parallel to 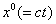-axis. Therefore the action of the standing particle during time interval 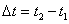becomes
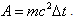(6)
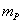Now, we suppose that the standing particle has Planck mass, , and that it moves along 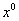-axis by Planck length, 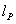. Then for the action in (6), we have
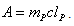(7)
If we use
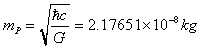and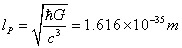
for Planck mass, 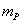, and Planck length, 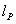, [4] we get
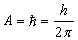(8)
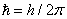for the action in (7). Where is Plank constant divided to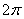, G is the universal Newtonian constant of gravitation, and c is the speed of light in vacuum.
Consequently, Planck constant is 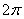times the amount of action of a standing particle which has Planck mass in a time interval by the Planck time.
According to Maupertuis’s definition of action, we can state that, indeed, Planck constant is a worth to be paid in order to progresses in time for a particle which has Planck mass. In other words, for moving in time of all bodies in universe a price to be paid. This price is times of Planck constant.

References

[1]  De Maupertuis, P. L. M., 1744, Accord de différentes loix de la nature qui avoient jusqu’ici paru incompatibles. Mém. Ac.Sc. Paris, 417–426.
[2]  De Maupertuis, P. L. M., 1746, Les loix du mouvement et du repos déduites d'un principe metaphysique. Histoire de l'Académie Royale des Sciences et des Belles Lettres. 267-294.
[3]  Landau, L. D. and Lifshitz, E. M., 1975, The Classical Theory of Fields, Pergamon Press, Oxford.
[4]  Lawrie, I. D., 2002, A Unified Grand Tour of Theoretical Physics, Institute of Physics Publishing, Bristol and Philadelphia.