A. A. Gavrilieva1, Yu. G. Gubarev2, 3, M. P. Lebedev1
1Department of Physical Chemistry for Materials and Technology, Larionov Institute of Physics and Technology Problems of the North SB RAS, Yakutsk, 677980, Russian Federation
2Laboratory of Fluid and Gas Vortical Motions, Lavrentyev Institute of Hydrodynamics SB RAS, Novosibirsk, 630090, Russian Federation
3Department of Differential Equations, Faculty of Mechanics and Mathematics, Novosibirsk National Research State University, Novosibirsk, 630090, Russian Federation
Correspondence to: Yu. G. Gubarev, Laboratory of Fluid and Gas Vortical Motions, Lavrentyev Institute of Hydrodynamics SB RAS, Novosibirsk, 630090, Russian Federation.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The linear stability problem of steady-state plane-parallel shear flows of a continuously stratified in density inviscid incompressible fluid in the gravity field between two immovable impermeable solid parallel planes in the Boussinesq approximation is studied. With the use of the direct Lyapunov method, it is proved that from the theoretical consideration (on semi-infinite temporal intervals) these flows are absolutely unstable with respect to small plane perturbations. Namely, a priory lower estimate is constructed; the estimate displays exponential in time growth of the considered perturbations. At that increment of containing in this estimate exponent is any positive constant. Using the direct Lyapunov method, constructive sufficient conditions of practical instability (on finite temporal intervals) are also found for these flows with respect to small plane perturbations
Keywords:
an IdealStratified Fluid, the Boussinesq Approximation, Steady-State Plane-Parallel Shear Flows, the Direct Lyapunov Method, an Absolute Theoretical Instability, a Priory Lower Estimate, Conditions of Practical Instability
Cite this paper: A. A. Gavrilieva, Yu. G. Gubarev, M. P. Lebedev, Rapid Approach to Resolving the Adequacy Problem of Mathematical Modeling of Physical Phenomena by the Example of Solving One Problem of Hydrodynamic Instability, International Journal of Theoretical and Mathematical Physics, Vol. 3 No. 4, 2013, pp. 123-129. doi: 10.5923/j.ijtmp.20130304.05.
1. Introduction
The stability problem of steady - state plane-parallel shear flows of a continuously stratified in density inviscidincompressible fluid in the gravity field in the Boussinesqapproximation with respect to small plane perturbations is one of fundamental problems in hydrodynamics, meteorology,oceanography and other related fields of science[1], has not lost its urgency in our time too. The most important application of this mathematical model in practice is the description of processes of wave motions propagation on reservoirssurfaces, when density distributions weakly differ from constant values, vertical scales of movements are small compared with characteristic depths, and Mach numbers are much smaller than unity.Basic results on stability studying of steady-state plane- parallel shear flows of a continuously stratified in density inviscid incompressible fluid in the gravity field between two immovable impermeable solid parallel planes in the Boussinesq approximation with respect to small plane perturbations are found by spectral method with use of integral relations[2–4]. Unfortunately, these results are correct just for perturbations as normal modes[1, 4]. Moreover, the consequence of integral ratios application is that all admissible perturbations as normal modes are not really taken into account, but only those that satisfy the additional requirement to Taylor-Goldstein differential operator[2–4].At last, as follows from energy reasoning given in work[5], in theoretical sense only states of rest with fluid density increasing towards the bottom plane are stable with respect to such subclass of small plane perturbations that for it small perturbations of studied fluid density are equal to zero on boundary. However, imposing of arbitrarily weak shear of fluid velocity destabilizes these rest states. Moreover, except for states of rest considered in article[5], it isn't possible to find conditions of theoretical stability for any steady-state flows of studied fluid with respect to small planeperturbations by means of energy reasons.All this pushes to make the assumption that there is an absolute theoretical instability of steady-state plane-parallel shear flows of a continuously stratified in density inviscid incompressible fluid in the gravity field in the Boussinesq approximation with respect to small plane perturbations. If this assumption is confirmed, it will mean that themathematical model of a continuously stratified in density inviscid incompressible fluid in the Boussinesq approximationdescribes steady-state plane-parallel shear flows in the gravity field inadequately. Extended above assumption of absolute instability of the studied steady-state plane-parallel shear flows in theoretical sense can be verified by the direct Lyapunov method[6–8] ― the most powerful analytical method of the mathematicaltheory of hydrodynamic stability. However, the main difficulty with using this method is that until now regular ways for construction of growing Lyapunov functionals have been unknown.Fortunately, the analytical technique[6] which allows to receive results and about theoretical (on semi-infinite intervals of time), and about practical (on finite temporary intervals) instability of those or other considered steady-state flows of fluids, gases or plasma with respect to small plane perturbations has been offered recently. The main point of the new technique consists in algorithmic constructing of Lyapunov functionals, being characterized, on the one hand, monotonous growth over time in chime with properties of solutions to the corresponding initial-boundary valueproblems for small perturbations, and the other ― such dependence form on small perturbations that growth of smallperturbations over time according to Lyapunov definition ofinstability[7] follows from increase of these functionals in time. At that, arising conditions for Lyapunov functionals increase with time just will be desirable sufficient conditions for either theoretical or practical instability of studied flows with respect to small plane perturbations. It is remarkable that for application of this technique it isn't necessary to know the specific type of solutions to the boundary and/or the mixed problems which describe the studied flows andperturbations[6].Thus, in this work absolute instability in theoretical sense will be proved by the direct Lyapunov method[6–8] for steady-state plane-parallel shear flows of a continuously stratified in density inviscid incompressible fluid in the gravity field between two immovable impermeable solid parallel planes in the Boussinesq approximation with respect to small plane perturbations. Besides, a priory lower estimate which will show exponential growth over time of the considered small perturbations will be constructed. At last, constructive sufficient conditions of practical instability for the studied flows with respect to small plane perturbations will be received.
2. Formulation of the Exact and the Linearized Problems
Unsteady-state plane flows of an ideal heterogeneous in density incompressible fluid in the gravity field between two immovable impermeable solid parallel planes in the Boussinesq approximation are considered. In a consent with this approximation, we neglect density changes when it concerns their influence on inertia, but, by no means, not weight changes (or buoyancy) of fluid[9].These flows are described by evolutionary solutions to the initial-boundary value problem[1–3, 9]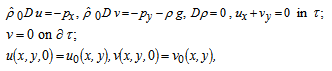 | (1) |
where 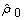 is a constant average density of fluid,
is a constant average density of fluid, 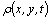 ― its perturbations;
― its perturbations; 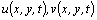 are components of the fluid velocity field;
are components of the fluid velocity field; 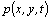 is the pressure field perturbations;
is the pressure field perturbations; 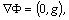
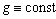 ― the potential field of gravity;
― the potential field of gravity; 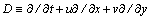 is a differential operator;
is a differential operator; 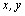 are Cartesian coordinates;
are Cartesian coordinates; 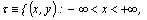
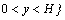 is the domain of fluid flow;
is the domain of fluid flow; 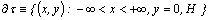 ― its boundary;
― its boundary; 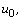
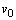 are the initial components of the fluid velocity field;
are the initial components of the fluid velocity field; 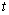 is the time;
is the time; 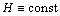 ― the width of the gap between the walls. Independent variables as subindexes stand for partial derivatives of desired functions. As assumed, the initial components
― the width of the gap between the walls. Independent variables as subindexes stand for partial derivatives of desired functions. As assumed, the initial components 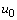 and
and 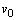 of the fluid velocity field turn the fourth relation of the mixed problem (1) into the identity. Moreover,
of the fluid velocity field turn the fourth relation of the mixed problem (1) into the identity. Moreover, 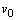 is assumed to satisfy the fifth relation in the same problem.If solutions to the initial-boundary value problem (1) are periodic or located along x-axis, this problem possesses the energy integral in the form
is assumed to satisfy the fifth relation in the same problem.If solutions to the initial-boundary value problem (1) are periodic or located along x-axis, this problem possesses the energy integral in the form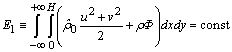 | (2) |
Moreover, the mixed problem (1) possesses one more integral of motion. Really, by means of introducing into consideration the function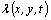 , which retains its values in any fluid particle as it moves (
, which retains its values in any fluid particle as it moves (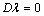 ), the integral
), the integral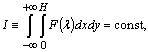 | (3) |
where 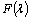 is an arbitrary function of its argument, stays a constant one on evolutional solutions to the initial-boundary value problem (1). The mixed problem (1) has exact stationary solutions of the form
is an arbitrary function of its argument, stays a constant one on evolutional solutions to the initial-boundary value problem (1). The mixed problem (1) has exact stationary solutions of the form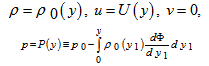 | (4) |
(here 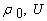 are an arbitrary functions in independent variable
are an arbitrary functions in independent variable 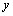 ,
, 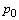 is an additive constant,
is an additive constant, 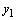 is a integration variable). These solutions correspond to the steady-state plane-parallel shear flows of a continuously stratified in density inviscid incompressible fluid in the gravity field between two immovable impermeable solid parallel planes in the Boussinesq approximation.Further consideration is aimed to answer the question if the stationary solutions (4) can be stable ones with respect to small plane perturbations.With this aim in mind, we linearize the initial-boundary value problem (1) in the vicinity of the exact stationary solutions (4) and finally arrive at the mixed problem:
is a integration variable). These solutions correspond to the steady-state plane-parallel shear flows of a continuously stratified in density inviscid incompressible fluid in the gravity field between two immovable impermeable solid parallel planes in the Boussinesq approximation.Further consideration is aimed to answer the question if the stationary solutions (4) can be stable ones with respect to small plane perturbations.With this aim in mind, we linearize the initial-boundary value problem (1) in the vicinity of the exact stationary solutions (4) and finally arrive at the mixed problem: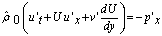 | (5) |
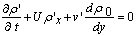 ,
, 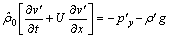 ,
,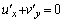 in
in 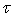 ;
;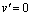 on
on 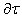 ;
;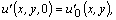
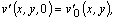 where
where 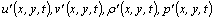 are small plane perturbations of velocity
are small plane perturbations of velocity 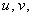 density
density 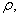 and pressure
and pressure 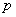 fields,
fields, 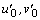 are the initial components of the perturbed field of fluid velocity. As assumed, the function
are the initial components of the perturbed field of fluid velocity. As assumed, the function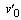 , firstly, turns the fifth relation of the initial-boundary value problem (5) into the identity and, secondly, satisfies the fourth relation of the same problem together with the function
, firstly, turns the fifth relation of the initial-boundary value problem (5) into the identity and, secondly, satisfies the fourth relation of the same problem together with the function 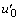 .Unfortunately (at least, as of today), the linear analogue of the energy integral for the mixed problem (5) has not yet been detected by means of the energy considerations.
.Unfortunately (at least, as of today), the linear analogue of the energy integral for the mixed problem (5) has not yet been detected by means of the energy considerations.
3. A Priori Exponential Lower Estimate for Growth of Small Plane Perturbations
Next, by the direct Lyapunov method it will be proved that steady-state flows (4) are absolutely unstable in theoretical consideration with respect to small plane perturbations (5).In order to demonstrate theoretical instability of astationary solution (4) of the initial-boundary value problem (1) with respect to small plane perturbations (5) we need at least one of these perturbations, but with the exponential time growth.From the above reasoning, the desired perturbation is sought in such subclass of plane flows that its small plane perturbations (5) are deviations of fluid particles motion paths from the corresponding stream lines of steady-state flows (4). The easiest description for these perturbations can be obtained with the use of the Lagrangian displacements field 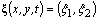 [10] which is given by the equations
[10] which is given by the equations 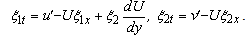 | (6) |
In view of the relations (6), the mixed problem (5) can be rewritten in the form: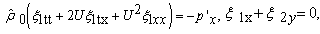 | (7) |
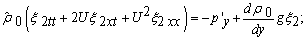
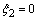 on
on 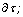
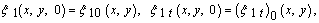
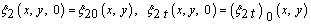 (here
(here 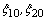 are the initial components of the Lagrangian displacements field
are the initial components of the Lagrangian displacements field 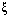 ;
; 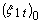 and
and 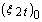 are the initial components of its first order time partial derivative). As assumed, the functions
are the initial components of its first order time partial derivative). As assumed, the functions 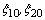 turn the second equation of the system (7) into the identity. Moreover, the function
turn the second equation of the system (7) into the identity. Moreover, the function 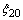 is assumed to satisfy the fourth equality in the same system.In the subclass (6) linear analogue of energy integral for the initial-boundary value problem (7) are represented by next form
is assumed to satisfy the fourth equality in the same system.In the subclass (6) linear analogue of energy integral for the initial-boundary value problem (7) are represented by next form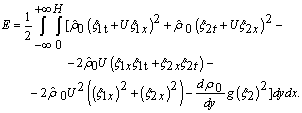 | (8) |
Indeed, by direct calculations it isn’t hard to obtain that the first variation 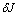 of integral
of integral 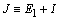 (2), (3) is equal to zero on stationary solutions (4) if and only if by choosing of function
(2), (3) is equal to zero on stationary solutions (4) if and only if by choosing of function 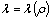 form the first variation of density perturbations on boundary
form the first variation of density perturbations on boundary 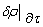 becomes equal to zero. At the same time, the second variation
becomes equal to zero. At the same time, the second variation 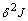 of integral
of integral 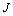 is coincident in the form with functional
is coincident in the form with functional 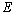 (8)[5].The integrand expression (8) has the constant-sign property only on states of rest and only when the following condition on density distribution of considered fluid
(8)[5].The integrand expression (8) has the constant-sign property only on states of rest and only when the following condition on density distribution of considered fluid 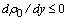 is satisfied. Superimposing arbitrarily weak speed shift destabilizes rest states in the sense that the constant-sign of integrand expression (8) is broken. As a result, the stability condition for steady-state flows (4) with respect to small pla- ne perturbations (6), (7) doesn’t exist. It is significant that lo- cal Richardson number
is satisfied. Superimposing arbitrarily weak speed shift destabilizes rest states in the sense that the constant-sign of integrand expression (8) is broken. As a result, the stability condition for steady-state flows (4) with respect to small pla- ne perturbations (6), (7) doesn’t exist. It is significant that lo- cal Richardson number 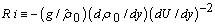 doesn't appear in coefficients of integrand expression (8). This fact maintains that local Richardson number doesn't arise as the stability condition from energetic reasoning[5].To further study, it is convenient to use the linear analogue of energy integral (8) in the form
doesn't appear in coefficients of integrand expression (8). This fact maintains that local Richardson number doesn't arise as the stability condition from energetic reasoning[5].To further study, it is convenient to use the linear analogue of energy integral (8) in the form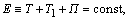 | (9) |
where 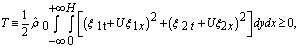
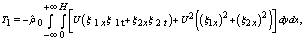
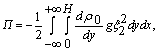 and also to introduce into the presentation an auxiliary functional in form[6]
and also to introduce into the presentation an auxiliary functional in form[6]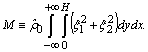 | (10) |
Actually, if we differentiate the integral 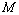 (10) by its argument
(10) by its argument 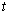 twice, transform the result with the use of relations (6), (7), and (9), it is not hard to arrive at the so-called virial equality[10]
twice, transform the result with the use of relations (6), (7), and (9), it is not hard to arrive at the so-called virial equality[10]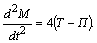 | (11) |
It should be noted that by arbitrary constant value 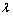 the non-negative functional can be constructed of integrals
the non-negative functional can be constructed of integrals 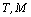 , and
, and 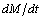 in the form
in the form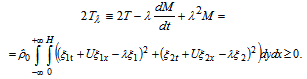 | (12) |
Excepting integral 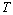 from expression (12) by relation (11) and using notation
from expression (12) by relation (11) and using notation 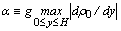 , it is possible to construct the differential inequality in form
, it is possible to construct the differential inequality in form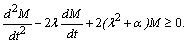 | (13) |
Now, if constant value is satisfied to the requirement 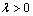 , and, by analogy to monographs[6, 11], supplemental conditions in the form
, and, by analogy to monographs[6, 11], supplemental conditions in the form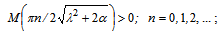 | (14) |
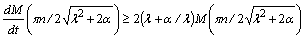 ;
;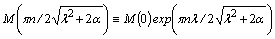 ,
,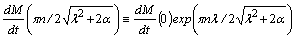 are added to the equation (13) that from it, under these conditions, the desired a priori exponential on the time lower estimate
are added to the equation (13) that from it, under these conditions, the desired a priori exponential on the time lower estimate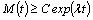 | (15) |
will arise with the need (here 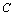 is the known positive constant).It is worth noting that the class of the mixed problem (6), (7) solutions, which grow with time in accordance with the constructed estimate (15), with an additional conditions
is the known positive constant).It is worth noting that the class of the mixed problem (6), (7) solutions, which grow with time in accordance with the constructed estimate (15), with an additional conditions 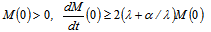 | (16) |
on the initial data 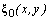 and
and 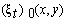 is not empty: 1) since the initial-boundary value problem (6), (7) is linear, then it is solvable with respect to small plane perturbations in the form of normal waves[4, 11]; 2) as the functional
is not empty: 1) since the initial-boundary value problem (6), (7) is linear, then it is solvable with respect to small plane perturbations in the form of normal waves[4, 11]; 2) as the functional 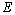 (8) has not the constant-sign property, the mixed problem (6), (7) is also solvable with respect to the rising over time small plane perturbations in the form of normal waves[6, 11]; 3) every growing with time solution of the initial-boundary value problem (6), (7), corresponding to the small plane disturbance in the form of normal wave, will be, due to arbitrariness of positive constant
(8) has not the constant-sign property, the mixed problem (6), (7) is also solvable with respect to the rising over time small plane perturbations in the form of normal waves[6, 11]; 3) every growing with time solution of the initial-boundary value problem (6), (7), corresponding to the small plane disturbance in the form of normal wave, will be, due to arbitrariness of positive constant 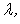 satisfy the differential inequality (13), the countable set of conditions (14) and the lower estimate (15) identically and automatically[6, 11].Consequently, there are increasing in time solutions to the mixed problem (6), (7), (16), which meet the small plane perturbations in the form of normal waves, in fact.In turn, the relation (15) demonstrates graphically that, according to the Lyapunov definition of instability[7], as minimum, one small plane perturbation (6), (7), (16) of steady-state plane-parallel shear flows (4) of an ideal stratified fluid grows over time, at that not slower than exponentially. Since this relation is obtained without involvement of any requirements of a restrictive nature to steady-state flows (4), it is precisely this fact that testifies to the absolute theoretical instability of the latter with respect to small plane perturbations (6), (7), (16).It is also worth noticing that in the given paper the integral
satisfy the differential inequality (13), the countable set of conditions (14) and the lower estimate (15) identically and automatically[6, 11].Consequently, there are increasing in time solutions to the mixed problem (6), (7), (16), which meet the small plane perturbations in the form of normal waves, in fact.In turn, the relation (15) demonstrates graphically that, according to the Lyapunov definition of instability[7], as minimum, one small plane perturbation (6), (7), (16) of steady-state plane-parallel shear flows (4) of an ideal stratified fluid grows over time, at that not slower than exponentially. Since this relation is obtained without involvement of any requirements of a restrictive nature to steady-state flows (4), it is precisely this fact that testifies to the absolute theoretical instability of the latter with respect to small plane perturbations (6), (7), (16).It is also worth noticing that in the given paper the integral 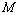 (10) exactly serves as the Lyapunov functional which grows in time in accordance with the motion equations of the initial-boundary value problem (6), (7), (16). The distinctive feature of this growth represents a lot of freedom, which is preserved for the positive constant
(10) exactly serves as the Lyapunov functional which grows in time in accordance with the motion equations of the initial-boundary value problem (6), (7), (16). The distinctive feature of this growth represents a lot of freedom, which is preserved for the positive constant 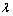 in the exponent from the right part of the lower estimate (15). This freedom, among other things, allows us to interpret every solution of the mixed problem (6), (7), (16), which increases with time according to the found priori exponential lower estimate (15), as an analogue of Hadamard example for incorrectness[12]. Finally, for small plane perturbations (6), (7), (16)inequalities of relations system (14) are sufficient conditions for practical linear instability[13, 14] of steady-state plane- parallel shear flows (4) of inviscid stratified fluid, but for small plane perturbations (6), (7), (16) in the form of normal waves ― necessary and sufficient (thanks to the fact that the positive constant
in the exponent from the right part of the lower estimate (15). This freedom, among other things, allows us to interpret every solution of the mixed problem (6), (7), (16), which increases with time according to the found priori exponential lower estimate (15), as an analogue of Hadamard example for incorrectness[12]. Finally, for small plane perturbations (6), (7), (16)inequalities of relations system (14) are sufficient conditions for practical linear instability[13, 14] of steady-state plane- parallel shear flows (4) of inviscid stratified fluid, but for small plane perturbations (6), (7), (16) in the form of normal waves ― necessary and sufficient (thanks to the fact that the positive constant 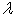 is arbitrary one as for the rest).It is also important that these conditions for practicallinear instability are characterized by constructiveness, allowing their use for the purposes of testing and control during physical experiments and numerical calculations.Indeed, let, for example, we need to develop atechnological process, which is based on the use of steady-state flows (4).In order for this process to be reliable in operation, it is necessary to ensure its practical stability with respect to all possible disturbances. In particular, this process must be stable in a practical sense with respect to small planeperturbations (6), (7), (16) in the form of normal waves.This result can be achieved by construction the numerical model, which corresponds to the linearized initial-boundary value problem (6), (7), (16), with the control in reference temporal points
is arbitrary one as for the rest).It is also important that these conditions for practicallinear instability are characterized by constructiveness, allowing their use for the purposes of testing and control during physical experiments and numerical calculations.Indeed, let, for example, we need to develop atechnological process, which is based on the use of steady-state flows (4).In order for this process to be reliable in operation, it is necessary to ensure its practical stability with respect to all possible disturbances. In particular, this process must be stable in a practical sense with respect to small planeperturbations (6), (7), (16) in the form of normal waves.This result can be achieved by construction the numerical model, which corresponds to the linearized initial-boundary value problem (6), (7), (16), with the control in reference temporal points 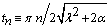
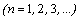 for the truth of the inequalities from the relations system (14). In the course of this model construction, it requires main efforts to focus on the fact that the inequalities of the relations system (14) were not valid because of those or other artificially induced external influences on the unsteady-state flows (6), (7) (for example, due to the initial conditions (16) violation).In the end, the practical stability of the developed technological process will be guaranteed, at the least, with respect to small plane perturbations (6), (7), (16) in the form of normal waves.Unfortunately, to date, the problem of constructing the numerical model described above has not been solved yet and so far only waits for the moment when specialists will turn their attention on it.Finally, it will be realized the comparison of this article results with the well-known result of the stability spectral theory for steady-state plane-parallel shear flows of a continuously stratified in density inviscid incompressible fluid in the gravity field between two immovable impermeable solid parallel planes in the Boussinesq approximation, which was obtained earlier by the integral relations method for the small plane perturbations in the form of normal waves ― the Miles theorem[2–4].
for the truth of the inequalities from the relations system (14). In the course of this model construction, it requires main efforts to focus on the fact that the inequalities of the relations system (14) were not valid because of those or other artificially induced external influences on the unsteady-state flows (6), (7) (for example, due to the initial conditions (16) violation).In the end, the practical stability of the developed technological process will be guaranteed, at the least, with respect to small plane perturbations (6), (7), (16) in the form of normal waves.Unfortunately, to date, the problem of constructing the numerical model described above has not been solved yet and so far only waits for the moment when specialists will turn their attention on it.Finally, it will be realized the comparison of this article results with the well-known result of the stability spectral theory for steady-state plane-parallel shear flows of a continuously stratified in density inviscid incompressible fluid in the gravity field between two immovable impermeable solid parallel planes in the Boussinesq approximation, which was obtained earlier by the integral relations method for the small plane perturbations in the form of normal waves ― the Miles theorem[2–4].
4. The Miles Theorem
Evolutionary solutions to the mixed problem (6), (7) of the form 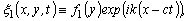 | (17) |
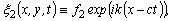
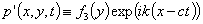 (here
(here 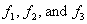 are arbitrary functions of its argument;
are arbitrary functions of its argument; 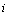 is the imaginary unit;
is the imaginary unit; 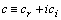 , an arbitrary complex constant;
, an arbitrary complex constant; 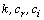 are arbitrary real constants) are considered.Substituting the relations (17) into the motion equations and the boundary condition of system (7), we conclude that the functions
are arbitrary real constants) are considered.Substituting the relations (17) into the motion equations and the boundary condition of system (7), we conclude that the functions 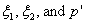 of the form (17) indeed satisfy the initial-boundary problem (6), (7) if the functions
of the form (17) indeed satisfy the initial-boundary problem (6), (7) if the functions 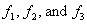 are solutions to the system of ordinary differential equations
are solutions to the system of ordinary differential equations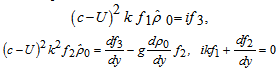 | (18) |
supplemented by the boundary conditions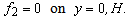 | (19) |
Excluding the functions 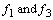 from the system (18), we can obtain the so-called Taylor-Goldstein equation[2, 4] for the function
from the system (18), we can obtain the so-called Taylor-Goldstein equation[2, 4] for the function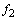 :
: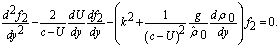 | (20) |
Including the new dependent variable 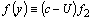 ,we obtain the final version of the boundary value problem (19), (20):
,we obtain the final version of the boundary value problem (19), (20):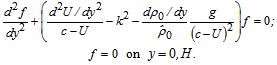 | (21) |
Following Miles, we need to make yet another substitution of the sought function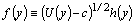 , and the received after this substitution relation to multiply by the complex-conjugate function
, and the received after this substitution relation to multiply by the complex-conjugate function 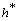 and to separate its imaginary part:
and to separate its imaginary part: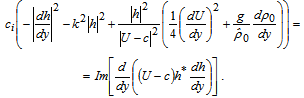 | (22) |
Approved by[2-4] that the equality (22) integration over the layer cross-section between two immovable impermeable solid parallel planes with the use of boundary conditions (21) gives the relation in the form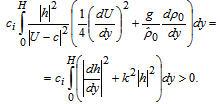 | (23) |
From this relation it follows that the exponentially growing (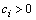 ) small plane perturbations (6), (7) in the form of normal waves (17) are able to convert it into an identity if and only if
) small plane perturbations (6), (7) in the form of normal waves (17) are able to convert it into an identity if and only if 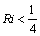 at least at one point within the domain of the fluid flow.In the end, it is established the sufficient condition
at least at one point within the domain of the fluid flow.In the end, it is established the sufficient condition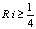 | (24) |
for the theoretical stability of the exact stationary solutions (4) to the mixed problem (1) with respect to small plane perturbations (6), (7) in the form of normal waves (17) (the Miles theorem[2-4]).However, as it is demonstrated below, the ratio (23) follows from equation (22) not for all functions 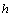 .In fact, if the integral of the right-hand part of the equality (22) is rewritten in the form
.In fact, if the integral of the right-hand part of the equality (22) is rewritten in the form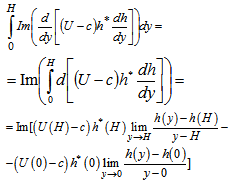 | (25) |
then the latter implies that the situation is possible that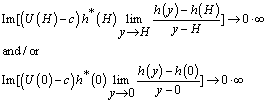 | (26) |
for the reason that the function 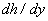 consists of a countable set of branches. Examples of these functions
consists of a countable set of branches. Examples of these functions 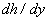 represent logarithmic, inverse trigonometric and other functions.Specifically, as the function
represent logarithmic, inverse trigonometric and other functions.Specifically, as the function 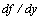 is not contained in the formulation of the boundary value problem (21), then there is no way to select one or the other branch of functions
is not contained in the formulation of the boundary value problem (21), then there is no way to select one or the other branch of functions 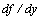 and
and 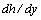 uniquely. Therefore, all branches of the function
uniquely. Therefore, all branches of the function 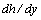 are equitable, so that the integral (25) must vanish for all countable set of the function
are equitable, so that the integral (25) must vanish for all countable set of the function 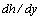 branches as a whole, and this is an occasion for the emergence of the type
branches as a whole, and this is an occasion for the emergence of the type 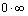 (26) uncertainty.From the foregoing it follows that the functions
(26) uncertainty.From the foregoing it follows that the functions 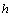 with the first order derivatives
with the first order derivatives 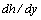 , containing a countable set of branches, are not covered by the Miles theorem (24). It is these functions that will give the counter-examples to this theorem.As a result, the Miles theorem (24)[2-4] is right not for all functions
, containing a countable set of branches, are not covered by the Miles theorem (24). It is these functions that will give the counter-examples to this theorem.As a result, the Miles theorem (24)[2-4] is right not for all functions 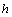 (22), but only for their subclass with derivatives
(22), but only for their subclass with derivatives 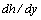 , which consist of a finite number of branches. That’s what says for the fact that: 1) the condition (24) of theoretical linear stability is not only sufficient but also necessary in nature, and besides with respect to the adjective partial class of small plane perturbations (5) in the form of normal waves (6), (7), (17), (23); 2) no contradictions between the Miles theorem[2-4] and the absolute theoretical linear instability of the steady-state flows (4), obtained in the present work. By the way, if the investigated fluid is homogeneous in density (so that the Taylor-Goldstein equation becomes the Rayleigh equation, and the Miles theorem reduces to the Rayleigh theorem), then it is proved in the publications[11, 15] that the subclass of functions, which correspond to functions
, which consist of a finite number of branches. That’s what says for the fact that: 1) the condition (24) of theoretical linear stability is not only sufficient but also necessary in nature, and besides with respect to the adjective partial class of small plane perturbations (5) in the form of normal waves (6), (7), (17), (23); 2) no contradictions between the Miles theorem[2-4] and the absolute theoretical linear instability of the steady-state flows (4), obtained in the present work. By the way, if the investigated fluid is homogeneous in density (so that the Taylor-Goldstein equation becomes the Rayleigh equation, and the Miles theorem reduces to the Rayleigh theorem), then it is proved in the publications[11, 15] that the subclass of functions, which correspond to functions 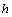 (22) with the first order derivatives
(22) with the first order derivatives 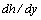 (26), containing a countable set of branches, serves as a non-empty set.
(26), containing a countable set of branches, serves as a non-empty set.
5. Conclusions
In this article the problem on linear stability ofsteady-state plane-parallel shear flows (4) in a continuously stratified in density inviscid incompressible fluid in the gravity field between two immovable impermeable solid parallel planes in the Boussinesq approximation is considered. By the direct Lyapunov method, it is proved that these flows are absolutely unstable in the theoretical sense with respect to small plane perturbations (6), (7), (16).Constructive sufficient conditions (see on the inequalities of therelations system (14)) for the practical linear instability are deduced. A priory lower estimate (15) is constructed, which displays exponential in time growth of the considered small perturbations. The application field of the Miles theorem (24) is strictly described, and it is also found that, by its nature, this theorem is both sufficient and necessary statement. It should be stressed that from the mathematical point of view the results of this work are, in the main, a priori, because the existence theorems of solutions to the studied initial-boundary value problems for systems of differential equations with partial derivatives have not been proved.Finally, regarding the question of whether themathematical model (1) of an ideal continuously stratified fluid in the Boussinesq approximation describes the steady-state plane-parallel shear flows (4) in the gravity field adequately, it must be said that it is not adequate, since this model has no theoretically stable solutions (4), which would correspond to the steady-state plane-parallel shear flows, although this kind of flows is observed in nature and is realized in applications.However, if conditions (refer to inequalities of theequations system (14)) of the practical linear instability are not met, the stationary solutions (4) to the mixed problem (1) will be stable with respect to small plane perturbations (6), (7), (16) in the form of normal waves (17) on those or any other finite time intervals.It follows that the mathematical model (1) does notadequately characterize the steady-state plane-parallel shear flows (4) in the theoretical sense (at the semi-infinite intervals of time), but adequately ― in the practical one (at the finite temporal intervals). In the end, constructive sufficient conditions (see oninequalities of the equations system (14)) for the practical linear instability can provide with a foundation for the creation of effective method for managing of the steady-state flows (4) in the real-time mode[11, 16].
ACKNOWLEDGEMENTS
The study was supported by the Ministry of education and science of Russian Federation, project 14.B37.21.0355.
References
| [1] | Dikii, L.A., 1976, Hydrodynamical stability and dynamics of atmosphere, Gidrometeoizdat, Leningrad (in Russian). |
| [2] | Miles, J.W., 1961, On the stability of heterogeneous shear flows, J. Fluid Мech., 10 (4), 496-508. |
| [3] | Howard, L.N., 1961, Note on a paper of John Miles, J. Fluid Мech., 10 (4), 509-512. |
| [4] | Drazin, P.G., 2002, Introduction to hydrodynamic stability, Cambridge University Press, Cambridge. |
| [5] | Vladimirov, V. A., 1987, Integrals of two-dimensionalmotions of a perfect incompressible fluid of nonuniform density, Fluid Dynamics, 22 (3), 340-343. |
| [6] | Gubarev, Yu.G., The development of Lyapunov's direct method in the application to new types of problems of hydrodynamic stability theory, in Progress in nonlinear analysis research, E. T. Hoffmann, Ed., Chap. 7. New York: Nova Science Publishers, 2009. Pp. 137-181. |
| [7] | Lyapunov, A.M., 1992, The general problem of the stability of motion, Taylor & Francis, London. |
| [8] | Chetaev, N.G., 1990, Stability of motion, Nauka, Moscow (in Russian). |
| [9] | Phillips, O. M., 1977, Dynamics of the upper ocean,Cambridge University Press, Cambridge. |
| [10] | Chandrasekhar, S., 1969, Ellipsoidal figures of equilibrium, Yale University Press, New Haven. |
| [11] | Gubarev, Yu.G., 2012, The direct Lyapunov method, The stability of quiescent states and steady-state flows of fluids and gases, Palmarium Academic Publishing, Saarbrücken (in Russian). |
| [12] | Godunov, S. K., 1979, Equations of mathematical physics, Nauka, Moscow (in Russian). |
| [13] | Karacharov, K.A., and Pilyutik, A.G., 1962, Introduction in technical theory of motion stability, Fizmatgiz, Moscow (in Russian). |
| [14] | La Salle, J.P., and Lefschetz, S., 1961, Stability by Lyapunov's direct method with applications, Acad. Press, New York. |
| [15] | Gubarev, Yu.G., 2007, On stability of steady-state plane-pa- rallel shearing flows in a homogeneous in density ideal incompressible fluid, Nonlinear Analysis: Hybrid Systems, 1 (1), 103-118. |
| [16] | Gubarev, Yu.G., 2011, Sufficient conditions for linear long- wave instability of steady-state axisymmetric flows of an ideal liquid with a free boundary in an azimuthal magnetic field, Technical Physics, 56 (3), 345-350. |

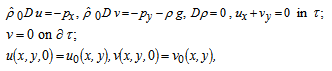
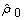 is a constant average density of fluid,
is a constant average density of fluid, 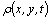 ― its perturbations;
― its perturbations; 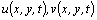 are components of the fluid velocity field;
are components of the fluid velocity field; 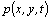 is the pressure field perturbations;
is the pressure field perturbations; 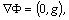
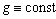 ― the potential field of gravity;
― the potential field of gravity; 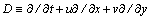 is a differential operator;
is a differential operator; 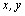 are Cartesian coordinates;
are Cartesian coordinates; 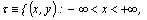
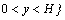 is the domain of fluid flow;
is the domain of fluid flow; 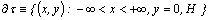 ― its boundary;
― its boundary; 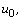
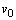 are the initial components of the fluid velocity field;
are the initial components of the fluid velocity field; 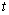 is the time;
is the time; 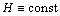 ― the width of the gap between the walls. Independent variables as subindexes stand for partial derivatives of desired functions. As assumed, the initial components
― the width of the gap between the walls. Independent variables as subindexes stand for partial derivatives of desired functions. As assumed, the initial components 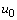 and
and 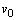 of the fluid velocity field turn the fourth relation of the mixed problem (1) into the identity. Moreover,
of the fluid velocity field turn the fourth relation of the mixed problem (1) into the identity. Moreover, 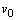 is assumed to satisfy the fifth relation in the same problem.If solutions to the initial-boundary value problem (1) are periodic or located along x-axis, this problem possesses the energy integral in the form
is assumed to satisfy the fifth relation in the same problem.If solutions to the initial-boundary value problem (1) are periodic or located along x-axis, this problem possesses the energy integral in the form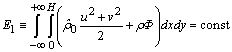
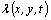 , which retains its values in any fluid particle as it moves (
, which retains its values in any fluid particle as it moves ( ), the integral
), the integral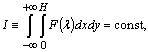
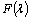 is an arbitrary function of its argument, stays a constant one on evolutional solutions to the initial-boundary value problem (1). The mixed problem (1) has exact stationary solutions of the form
is an arbitrary function of its argument, stays a constant one on evolutional solutions to the initial-boundary value problem (1). The mixed problem (1) has exact stationary solutions of the form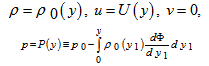
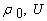 are an arbitrary functions in independent variable
are an arbitrary functions in independent variable 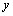 ,
, 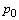 is an additive constant,
is an additive constant, 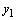 is a integration variable). These solutions correspond to the steady-state plane-parallel shear flows of a continuously stratified in density inviscid incompressible fluid in the gravity field between two immovable impermeable solid parallel planes in the Boussinesq approximation.Further consideration is aimed to answer the question if the stationary solutions (4) can be stable ones with respect to small plane perturbations.With this aim in mind, we linearize the initial-boundary value problem (1) in the vicinity of the exact stationary solutions (4) and finally arrive at the mixed problem:
is a integration variable). These solutions correspond to the steady-state plane-parallel shear flows of a continuously stratified in density inviscid incompressible fluid in the gravity field between two immovable impermeable solid parallel planes in the Boussinesq approximation.Further consideration is aimed to answer the question if the stationary solutions (4) can be stable ones with respect to small plane perturbations.With this aim in mind, we linearize the initial-boundary value problem (1) in the vicinity of the exact stationary solutions (4) and finally arrive at the mixed problem: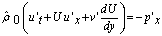
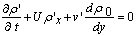 ,
, 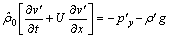 ,
,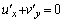 in
in  ;
; on
on 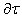 ;
;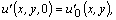
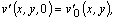 where
where 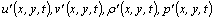 are small plane perturbations of velocity
are small plane perturbations of velocity 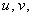 density
density 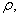 and pressure
and pressure 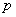 fields,
fields, 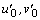 are the initial components of the perturbed field of fluid velocity. As assumed, the function
are the initial components of the perturbed field of fluid velocity. As assumed, the function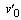 , firstly, turns the fifth relation of the initial-boundary value problem (5) into the identity and, secondly, satisfies the fourth relation of the same problem together with the function
, firstly, turns the fifth relation of the initial-boundary value problem (5) into the identity and, secondly, satisfies the fourth relation of the same problem together with the function 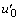 .Unfortunately (at least, as of today), the linear analogue of the energy integral for the mixed problem (5) has not yet been detected by means of the energy considerations.
.Unfortunately (at least, as of today), the linear analogue of the energy integral for the mixed problem (5) has not yet been detected by means of the energy considerations.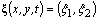 [10] which is given by the equations
[10] which is given by the equations 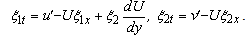
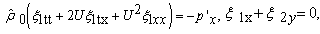
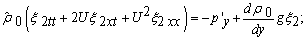
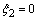 on
on 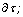
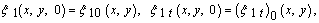
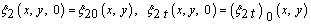 (here
(here 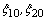 are the initial components of the Lagrangian displacements field
are the initial components of the Lagrangian displacements field 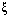 ;
; 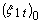 and
and 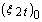 are the initial components of its first order time partial derivative). As assumed, the functions
are the initial components of its first order time partial derivative). As assumed, the functions 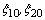 turn the second equation of the system (7) into the identity. Moreover, the function
turn the second equation of the system (7) into the identity. Moreover, the function 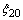 is assumed to satisfy the fourth equality in the same system.In the subclass (6) linear analogue of energy integral for the initial-boundary value problem (7) are represented by next form
is assumed to satisfy the fourth equality in the same system.In the subclass (6) linear analogue of energy integral for the initial-boundary value problem (7) are represented by next form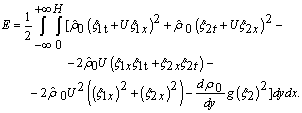
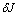 of integral
of integral 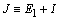 (2), (3) is equal to zero on stationary solutions (4) if and only if by choosing of function
(2), (3) is equal to zero on stationary solutions (4) if and only if by choosing of function 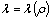 form the first variation of density perturbations on boundary
form the first variation of density perturbations on boundary 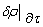 becomes equal to zero. At the same time, the second variation
becomes equal to zero. At the same time, the second variation 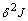 of integral
of integral 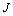 is coincident in the form with functional
is coincident in the form with functional 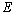 (8)[5].The integrand expression (8) has the constant-sign property only on states of rest and only when the following condition on density distribution of considered fluid
(8)[5].The integrand expression (8) has the constant-sign property only on states of rest and only when the following condition on density distribution of considered fluid 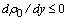 is satisfied. Superimposing arbitrarily weak speed shift destabilizes rest states in the sense that the constant-sign of integrand expression (8) is broken. As a result, the stability condition for steady-state flows (4) with respect to small pla- ne perturbations (6), (7) doesn’t exist. It is significant that lo- cal Richardson number
is satisfied. Superimposing arbitrarily weak speed shift destabilizes rest states in the sense that the constant-sign of integrand expression (8) is broken. As a result, the stability condition for steady-state flows (4) with respect to small pla- ne perturbations (6), (7) doesn’t exist. It is significant that lo- cal Richardson number 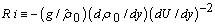 doesn't appear in coefficients of integrand expression (8). This fact maintains that local Richardson number doesn't arise as the stability condition from energetic reasoning[5].To further study, it is convenient to use the linear analogue of energy integral (8) in the form
doesn't appear in coefficients of integrand expression (8). This fact maintains that local Richardson number doesn't arise as the stability condition from energetic reasoning[5].To further study, it is convenient to use the linear analogue of energy integral (8) in the form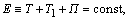
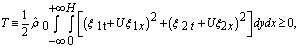
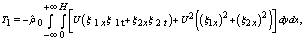
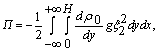 and also to introduce into the presentation an auxiliary functional in form[6]
and also to introduce into the presentation an auxiliary functional in form[6]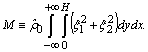
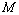 (10) by its argument
(10) by its argument 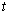 twice, transform the result with the use of relations (6), (7), and (9), it is not hard to arrive at the so-called virial equality[10]
twice, transform the result with the use of relations (6), (7), and (9), it is not hard to arrive at the so-called virial equality[10]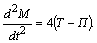
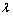 the non-negative functional can be constructed of integrals
the non-negative functional can be constructed of integrals 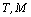 , and
, and 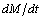 in the form
in the form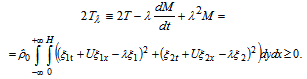
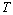 from expression (12) by relation (11) and using notation
from expression (12) by relation (11) and using notation 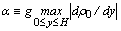 , it is possible to construct the differential inequality in form
, it is possible to construct the differential inequality in form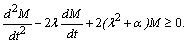
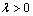 , and, by analogy to monographs[6, 11], supplemental conditions in the form
, and, by analogy to monographs[6, 11], supplemental conditions in the form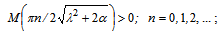
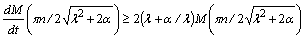 ;
;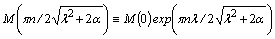 ,
,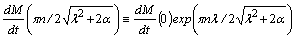 are added to the equation (13) that from it, under these conditions, the desired a priori exponential on the time lower estimate
are added to the equation (13) that from it, under these conditions, the desired a priori exponential on the time lower estimate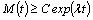
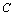 is the known positive constant).It is worth noting that the class of the mixed problem (6), (7) solutions, which grow with time in accordance with the constructed estimate (15), with an additional conditions
is the known positive constant).It is worth noting that the class of the mixed problem (6), (7) solutions, which grow with time in accordance with the constructed estimate (15), with an additional conditions 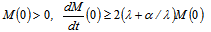
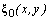 and
and 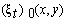 is not empty: 1) since the initial-boundary value problem (6), (7) is linear, then it is solvable with respect to small plane perturbations in the form of normal waves[4, 11]; 2) as the functional
is not empty: 1) since the initial-boundary value problem (6), (7) is linear, then it is solvable with respect to small plane perturbations in the form of normal waves[4, 11]; 2) as the functional 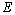 (8) has not the constant-sign property, the mixed problem (6), (7) is also solvable with respect to the rising over time small plane perturbations in the form of normal waves[6, 11]; 3) every growing with time solution of the initial-boundary value problem (6), (7), corresponding to the small plane disturbance in the form of normal wave, will be, due to arbitrariness of positive constant
(8) has not the constant-sign property, the mixed problem (6), (7) is also solvable with respect to the rising over time small plane perturbations in the form of normal waves[6, 11]; 3) every growing with time solution of the initial-boundary value problem (6), (7), corresponding to the small plane disturbance in the form of normal wave, will be, due to arbitrariness of positive constant 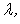 satisfy the differential inequality (13), the countable set of conditions (14) and the lower estimate (15) identically and automatically[6, 11].Consequently, there are increasing in time solutions to the mixed problem (6), (7), (16), which meet the small plane perturbations in the form of normal waves, in fact.In turn, the relation (15) demonstrates graphically that, according to the Lyapunov definition of instability[7], as minimum, one small plane perturbation (6), (7), (16) of steady-state plane-parallel shear flows (4) of an ideal stratified fluid grows over time, at that not slower than exponentially. Since this relation is obtained without involvement of any requirements of a restrictive nature to steady-state flows (4), it is precisely this fact that testifies to the absolute theoretical instability of the latter with respect to small plane perturbations (6), (7), (16).It is also worth noticing that in the given paper the integral
satisfy the differential inequality (13), the countable set of conditions (14) and the lower estimate (15) identically and automatically[6, 11].Consequently, there are increasing in time solutions to the mixed problem (6), (7), (16), which meet the small plane perturbations in the form of normal waves, in fact.In turn, the relation (15) demonstrates graphically that, according to the Lyapunov definition of instability[7], as minimum, one small plane perturbation (6), (7), (16) of steady-state plane-parallel shear flows (4) of an ideal stratified fluid grows over time, at that not slower than exponentially. Since this relation is obtained without involvement of any requirements of a restrictive nature to steady-state flows (4), it is precisely this fact that testifies to the absolute theoretical instability of the latter with respect to small plane perturbations (6), (7), (16).It is also worth noticing that in the given paper the integral 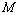 (10) exactly serves as the Lyapunov functional which grows in time in accordance with the motion equations of the initial-boundary value problem (6), (7), (16). The distinctive feature of this growth represents a lot of freedom, which is preserved for the positive constant
(10) exactly serves as the Lyapunov functional which grows in time in accordance with the motion equations of the initial-boundary value problem (6), (7), (16). The distinctive feature of this growth represents a lot of freedom, which is preserved for the positive constant 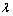 in the exponent from the right part of the lower estimate (15). This freedom, among other things, allows us to interpret every solution of the mixed problem (6), (7), (16), which increases with time according to the found priori exponential lower estimate (15), as an analogue of Hadamard example for incorrectness[12]. Finally, for small plane perturbations (6), (7), (16)inequalities of relations system (14) are sufficient conditions for practical linear instability[13, 14] of steady-state plane- parallel shear flows (4) of inviscid stratified fluid, but for small plane perturbations (6), (7), (16) in the form of normal waves ― necessary and sufficient (thanks to the fact that the positive constant
in the exponent from the right part of the lower estimate (15). This freedom, among other things, allows us to interpret every solution of the mixed problem (6), (7), (16), which increases with time according to the found priori exponential lower estimate (15), as an analogue of Hadamard example for incorrectness[12]. Finally, for small plane perturbations (6), (7), (16)inequalities of relations system (14) are sufficient conditions for practical linear instability[13, 14] of steady-state plane- parallel shear flows (4) of inviscid stratified fluid, but for small plane perturbations (6), (7), (16) in the form of normal waves ― necessary and sufficient (thanks to the fact that the positive constant 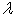 is arbitrary one as for the rest).It is also important that these conditions for practicallinear instability are characterized by constructiveness, allowing their use for the purposes of testing and control during physical experiments and numerical calculations.Indeed, let, for example, we need to develop atechnological process, which is based on the use of steady-state flows (4).In order for this process to be reliable in operation, it is necessary to ensure its practical stability with respect to all possible disturbances. In particular, this process must be stable in a practical sense with respect to small planeperturbations (6), (7), (16) in the form of normal waves.This result can be achieved by construction the numerical model, which corresponds to the linearized initial-boundary value problem (6), (7), (16), with the control in reference temporal points
is arbitrary one as for the rest).It is also important that these conditions for practicallinear instability are characterized by constructiveness, allowing their use for the purposes of testing and control during physical experiments and numerical calculations.Indeed, let, for example, we need to develop atechnological process, which is based on the use of steady-state flows (4).In order for this process to be reliable in operation, it is necessary to ensure its practical stability with respect to all possible disturbances. In particular, this process must be stable in a practical sense with respect to small planeperturbations (6), (7), (16) in the form of normal waves.This result can be achieved by construction the numerical model, which corresponds to the linearized initial-boundary value problem (6), (7), (16), with the control in reference temporal points 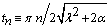
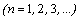 for the truth of the inequalities from the relations system (14). In the course of this model construction, it requires main efforts to focus on the fact that the inequalities of the relations system (14) were not valid because of those or other artificially induced external influences on the unsteady-state flows (6), (7) (for example, due to the initial conditions (16) violation).In the end, the practical stability of the developed technological process will be guaranteed, at the least, with respect to small plane perturbations (6), (7), (16) in the form of normal waves.Unfortunately, to date, the problem of constructing the numerical model described above has not been solved yet and so far only waits for the moment when specialists will turn their attention on it.Finally, it will be realized the comparison of this article results with the well-known result of the stability spectral theory for steady-state plane-parallel shear flows of a continuously stratified in density inviscid incompressible fluid in the gravity field between two immovable impermeable solid parallel planes in the Boussinesq approximation, which was obtained earlier by the integral relations method for the small plane perturbations in the form of normal waves ― the Miles theorem[2–4].
for the truth of the inequalities from the relations system (14). In the course of this model construction, it requires main efforts to focus on the fact that the inequalities of the relations system (14) were not valid because of those or other artificially induced external influences on the unsteady-state flows (6), (7) (for example, due to the initial conditions (16) violation).In the end, the practical stability of the developed technological process will be guaranteed, at the least, with respect to small plane perturbations (6), (7), (16) in the form of normal waves.Unfortunately, to date, the problem of constructing the numerical model described above has not been solved yet and so far only waits for the moment when specialists will turn their attention on it.Finally, it will be realized the comparison of this article results with the well-known result of the stability spectral theory for steady-state plane-parallel shear flows of a continuously stratified in density inviscid incompressible fluid in the gravity field between two immovable impermeable solid parallel planes in the Boussinesq approximation, which was obtained earlier by the integral relations method for the small plane perturbations in the form of normal waves ― the Miles theorem[2–4].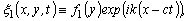
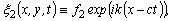
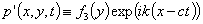 (here
(here 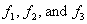 are arbitrary functions of its argument;
are arbitrary functions of its argument; 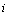 is the imaginary unit;
is the imaginary unit; 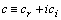 , an arbitrary complex constant;
, an arbitrary complex constant; 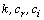 are arbitrary real constants) are considered.Substituting the relations (17) into the motion equations and the boundary condition of system (7), we conclude that the functions
are arbitrary real constants) are considered.Substituting the relations (17) into the motion equations and the boundary condition of system (7), we conclude that the functions 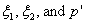 of the form (17) indeed satisfy the initial-boundary problem (6), (7) if the functions
of the form (17) indeed satisfy the initial-boundary problem (6), (7) if the functions 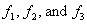 are solutions to the system of ordinary differential equations
are solutions to the system of ordinary differential equations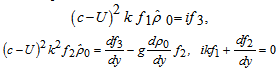
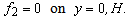
 from the system (18), we can obtain the so-called Taylor-Goldstein equation[2, 4] for the function
from the system (18), we can obtain the so-called Taylor-Goldstein equation[2, 4] for the function :
: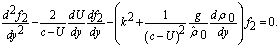
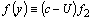 ,we obtain the final version of the boundary value problem (19), (20):
,we obtain the final version of the boundary value problem (19), (20):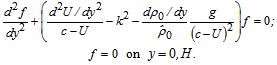
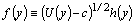 , and the received after this substitution relation to multiply by the complex-conjugate function
, and the received after this substitution relation to multiply by the complex-conjugate function 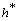 and to separate its imaginary part:
and to separate its imaginary part: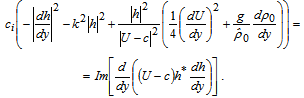
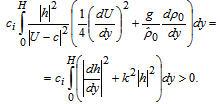
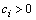 ) small plane perturbations (6), (7) in the form of normal waves (17) are able to convert it into an identity if and only if
) small plane perturbations (6), (7) in the form of normal waves (17) are able to convert it into an identity if and only if 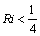 at least at one point within the domain of the fluid flow.In the end, it is established the sufficient condition
at least at one point within the domain of the fluid flow.In the end, it is established the sufficient condition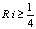
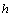 .In fact, if the integral of the right-hand part of the equality (22) is rewritten in the form
.In fact, if the integral of the right-hand part of the equality (22) is rewritten in the form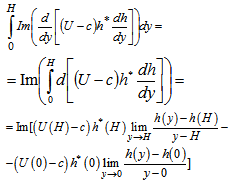
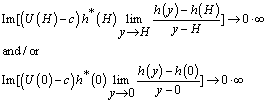
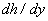 consists of a countable set of branches. Examples of these functions
consists of a countable set of branches. Examples of these functions 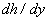 represent logarithmic, inverse trigonometric and other functions.Specifically, as the function
represent logarithmic, inverse trigonometric and other functions.Specifically, as the function 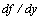 is not contained in the formulation of the boundary value problem (21), then there is no way to select one or the other branch of functions
is not contained in the formulation of the boundary value problem (21), then there is no way to select one or the other branch of functions 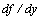 and
and 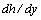 uniquely. Therefore, all branches of the function
uniquely. Therefore, all branches of the function 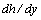 are equitable, so that the integral (25) must vanish for all countable set of the function
are equitable, so that the integral (25) must vanish for all countable set of the function 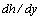 branches as a whole, and this is an occasion for the emergence of the type
branches as a whole, and this is an occasion for the emergence of the type 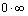 (26) uncertainty.From the foregoing it follows that the functions
(26) uncertainty.From the foregoing it follows that the functions 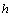 with the first order derivatives
with the first order derivatives 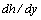 , containing a countable set of branches, are not covered by the Miles theorem (24). It is these functions that will give the counter-examples to this theorem.As a result, the Miles theorem (24)[2-4] is right not for all functions
, containing a countable set of branches, are not covered by the Miles theorem (24). It is these functions that will give the counter-examples to this theorem.As a result, the Miles theorem (24)[2-4] is right not for all functions 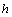 (22), but only for their subclass with derivatives
(22), but only for their subclass with derivatives 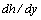 , which consist of a finite number of branches. That’s what says for the fact that: 1) the condition (24) of theoretical linear stability is not only sufficient but also necessary in nature, and besides with respect to the adjective partial class of small plane perturbations (5) in the form of normal waves (6), (7), (17), (23); 2) no contradictions between the Miles theorem[2-4] and the absolute theoretical linear instability of the steady-state flows (4), obtained in the present work. By the way, if the investigated fluid is homogeneous in density (so that the Taylor-Goldstein equation becomes the Rayleigh equation, and the Miles theorem reduces to the Rayleigh theorem), then it is proved in the publications[11, 15] that the subclass of functions, which correspond to functions
, which consist of a finite number of branches. That’s what says for the fact that: 1) the condition (24) of theoretical linear stability is not only sufficient but also necessary in nature, and besides with respect to the adjective partial class of small plane perturbations (5) in the form of normal waves (6), (7), (17), (23); 2) no contradictions between the Miles theorem[2-4] and the absolute theoretical linear instability of the steady-state flows (4), obtained in the present work. By the way, if the investigated fluid is homogeneous in density (so that the Taylor-Goldstein equation becomes the Rayleigh equation, and the Miles theorem reduces to the Rayleigh theorem), then it is proved in the publications[11, 15] that the subclass of functions, which correspond to functions 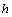 (22) with the first order derivatives
(22) with the first order derivatives 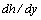 (26), containing a countable set of branches, serves as a non-empty set.
(26), containing a countable set of branches, serves as a non-empty set. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML