-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2013; 3(4): 109-116
doi:10.5923/j.ijtmp.20130304.03
Lagrangian for the Spinor Field in the Foldy – Wouthuysen Representation
Volodimir Simulik , Ivan Krivsky, Irina Lamer
Institute of Electron Physics, National Academy of Sciences of Ukraine, 21 Universitetska Street, 88000, Uzhgorod Ukraine
Correspondence to: Volodimir Simulik , Institute of Electron Physics, National Academy of Sciences of Ukraine, 21 Universitetska Street, 88000, Uzhgorod Ukraine.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The relativistic invariant Lagrange approach for the spinor field in the Foldy–Wouthuysen representation is constructed. In the procedure of postulating the Lagrangian, the analogy with the classical mechanics of the system with the arbitrary number degrees of freedom is used. Conservation laws in the terms of particle and antiparticle quantum-mechanical momentum-spin amplitdes are presented. 24 conserved quantities for the free spinor field are given. Ten of them are consequences of the Poincaré symmetry. 12 additional conservation laws are the consequences of the fact that in the Foldy–Wouthuysen representation spin and orbital parts of the Poincaré angular momentum are conserved independently. The conserved quantities of charge and of particle number are found as well.
Keywords: Spinor Field, Foldy–Wouthuysen Representation, Lagrange Approach, Noether Theorem, Conservation Laws
Cite this paper: Volodimir Simulik , Ivan Krivsky, Irina Lamer , Lagrangian for the Spinor Field in the Foldy – Wouthuysen Representation, International Journal of Theoretical and Mathematical Physics, Vol. 3 No. 4, 2013, pp. 109-116. doi: 10.5923/j.ijtmp.20130304.03.
Article Outline
1. Introduction
- Among the goals of this article the following two main points can be noted.(i) Construction of a mathematically well-defined Lagrangian, for which the Foldy–Wouthuysen(FW) equation [1] follows from the Euler–Lagrange equations.(ii) Application of the Lagrangian under consideration to the Noether analysis of the dynamical invariants of the spinor field in the FW representation.In spite of the fact that some advantages of the Dirac equation consideration in the FW representation are well known (see, e. g.,[1–6]), the acceptable Lagrange approach in this representation is not developed. The Lagrangian and the main conservation laws for the FW field
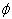 can be found in the papers[7, 8]. However, the author of[7, 8] has suggested a non-standard formulation of the least action principle. The derivatives of the infinite order from the field functions were used. The representation of the operator
can be found in the papers[7, 8]. However, the author of[7, 8] has suggested a non-standard formulation of the least action principle. The derivatives of the infinite order from the field functions were used. The representation of the operator 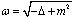 in the form of a series over the Laplace operator powers was used.Below we suggest the standard formulation of the least action principle and of the Lagrange approach to a free spinor field in the FW representation. Unlike[7, 8], our consideration is based[9] on the mathematically well-defined definition of the nonlocal (pseudodifferential) operator
in the form of a series over the Laplace operator powers was used.Below we suggest the standard formulation of the least action principle and of the Lagrange approach to a free spinor field in the FW representation. Unlike[7, 8], our consideration is based[9] on the mathematically well-defined definition of the nonlocal (pseudodifferential) operator 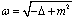 and its functions. We consider the integral form of such operators in the momentum representation of the Schwartz space
and its functions. We consider the integral form of such operators in the momentum representation of the Schwartz space  . The Noether analysis of the conservation laws for the spinor field in the Dirac theory is also a non-trivial problem. This results from the fact that the spin part of the total angular momentum generator does not commute with the Dirac Hamiltonian. Therefore, derivation of the spin conservation law in the Dirac theory requires additional non-Noether efforts even in obtaining the third component of the spin conserved quantity[10]. The special efforts in derivation of the spin conservation law can be found in[11] as well.The important advantage of the FW representation[1–3] is commutation of the spin operator with the FW Hamiltonian itself (the operator of angular momentum commutes here with the Hamiltonian as well). Therefore, having a well-defined Lagrangian for the free spinor field in the FW representation, we are able to find not only the 10 Poincaré conservation laws, but also 12 additional conservation laws. The additional conserved quantities are the Noether consequences of the following 12 operators: 3 of spin, 3 of pure Lorentz spin, 3 of angular momentum and 3 of pure Lorentz angular momentum operators, which in the FW representation are the independent symmetry operators. The conserved quantities of charge and number of particles are found. as well.The Lagrange approach for the spinor field under consideration is interesting for the construction of the quantum electrodynamics in the FW representation. The version of such quantum electrodynamics was suggested recently in[12–14]. In our approach to such theory, we start here from the construction of the Lagrange formalism for the free spinor field and from the Noether analysis of the corresponding dynamical invariants.The summary of our motivation is very simple. We consider the construction of the Lagrange approach for the spinor field in the FW representation because this problem was not solved before (even after 60 years of the introduction of the FW equation and corresponding representation). Moreover, the known Noether (based on the Noether theorem) analysis of the conservation laws for the free spinor field and for the Dirac equation is not sufficient (even in the best investigations like[10], where even 10 main conservation laws, which follow from the Poincaré symmetry, are not described completely). Below we hope to be able to fill this gap.
. The Noether analysis of the conservation laws for the spinor field in the Dirac theory is also a non-trivial problem. This results from the fact that the spin part of the total angular momentum generator does not commute with the Dirac Hamiltonian. Therefore, derivation of the spin conservation law in the Dirac theory requires additional non-Noether efforts even in obtaining the third component of the spin conserved quantity[10]. The special efforts in derivation of the spin conservation law can be found in[11] as well.The important advantage of the FW representation[1–3] is commutation of the spin operator with the FW Hamiltonian itself (the operator of angular momentum commutes here with the Hamiltonian as well). Therefore, having a well-defined Lagrangian for the free spinor field in the FW representation, we are able to find not only the 10 Poincaré conservation laws, but also 12 additional conservation laws. The additional conserved quantities are the Noether consequences of the following 12 operators: 3 of spin, 3 of pure Lorentz spin, 3 of angular momentum and 3 of pure Lorentz angular momentum operators, which in the FW representation are the independent symmetry operators. The conserved quantities of charge and number of particles are found. as well.The Lagrange approach for the spinor field under consideration is interesting for the construction of the quantum electrodynamics in the FW representation. The version of such quantum electrodynamics was suggested recently in[12–14]. In our approach to such theory, we start here from the construction of the Lagrange formalism for the free spinor field and from the Noether analysis of the corresponding dynamical invariants.The summary of our motivation is very simple. We consider the construction of the Lagrange approach for the spinor field in the FW representation because this problem was not solved before (even after 60 years of the introduction of the FW equation and corresponding representation). Moreover, the known Noether (based on the Noether theorem) analysis of the conservation laws for the free spinor field and for the Dirac equation is not sufficient (even in the best investigations like[10], where even 10 main conservation laws, which follow from the Poincaré symmetry, are not described completely). Below we hope to be able to fill this gap.2. Definitions, Notations and Some Justifications
- We use the standard relativistic notations. The metric tensor is given by
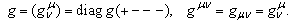 | (1) |
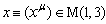 oursquare has the form
oursquare has the form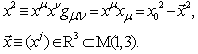 | (2) |
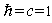 is taken. Here the Greek indices are changed in the range 0,1,2,3 ≡ 0,3, Latin — 1,3, the summation over a twice repeated index is implied. The Dirac
is taken. Here the Greek indices are changed in the range 0,1,2,3 ≡ 0,3, Latin — 1,3, the summation over a twice repeated index is implied. The Dirac 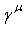 matrices in the standard Pauli–Dirac representation are used:
matrices in the standard Pauli–Dirac representation are used: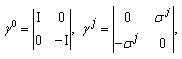 | (3) |
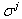 are the standard Pauli matrices.The analysis of the relativistic invariance of an arbitrary physical model demands as the first step consideration of its invariance with respect to the proper ortochronous Lorentz
are the standard Pauli matrices.The analysis of the relativistic invariance of an arbitrary physical model demands as the first step consideration of its invariance with respect to the proper ortochronous Lorentz 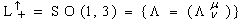 and Poincaré
and Poincaré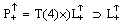 groups. This invariance in an arbitrary relativistic model is the allowance of the Einstein’s relativity principle in the form of special relativity. Note that the mathematical correctness requires to consider the invariance mentioned above as that with respect to the universal coverings
groups. This invariance in an arbitrary relativistic model is the allowance of the Einstein’s relativity principle in the form of special relativity. Note that the mathematical correctness requires to consider the invariance mentioned above as that with respect to the universal coverings 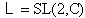 and
and 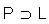 of the groups
of the groups 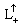 and
and 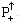 , respectively.Below we construct a relativistic invariant Lagrange approach for the spinor field in its canonical FW representation on the basis of the following principles. The quantum-mechanical rigged Hilbert space (both in the coordinate and momentum realizations of this space) is used. We do not appeal to the manifestly covariant conceptions and use some analogy with the Lagrange approach in the classical mechanics of systems with large (infinite) number of degrees of freedom. This analogy becomes complete in the case of a start from the momentum (more exactly – from the momentum-spin) realization of the state space of the FW field. The elements
, respectively.Below we construct a relativistic invariant Lagrange approach for the spinor field in its canonical FW representation on the basis of the following principles. The quantum-mechanical rigged Hilbert space (both in the coordinate and momentum realizations of this space) is used. We do not appeal to the manifestly covariant conceptions and use some analogy with the Lagrange approach in the classical mechanics of systems with large (infinite) number of degrees of freedom. This analogy becomes complete in the case of a start from the momentum (more exactly – from the momentum-spin) realization of the state space of the FW field. The elements 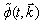 of such space are linked with those
of such space are linked with those 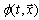 in the coordinate realization by the Fourier transformation:
in the coordinate realization by the Fourier transformation: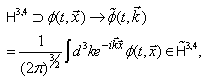 | (4) |
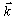 -realization is given by the Lebesgue measure
-realization is given by the Lebesgue measure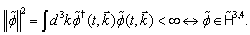 | (5) |
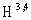 is the 4-component quantum-mechanical Hilbert space in the coordinate or
is the 4-component quantum-mechanical Hilbert space in the coordinate or 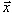 -realization
-realization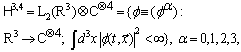 | (6) |
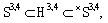 | (7) |
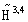
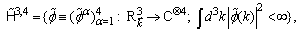 | (8) |
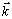 -realization, inserted into the rigged Hilbert space
-realization, inserted into the rigged Hilbert space 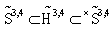 | (9) |
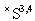 (the details of the application of the rigged Hilbert space can be found in[15]). Therefore, we deal here with the following situation.In the above formulae
(the details of the application of the rigged Hilbert space can be found in[15]). Therefore, we deal here with the following situation.In the above formulae 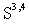 is the space of the 4-component Schwartz test functions over the
is the space of the 4-component Schwartz test functions over the 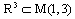 . The symbol «×» in
. The symbol «×» in 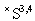 means that the space of the Schwartz generalized functions
means that the space of the Schwartz generalized functions 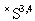 is conjugated to the Schwartz test function space
is conjugated to the Schwartz test function space 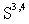 by the corresponding topology (see, e. g.,[16]). Strictly speaking, the mathematical correctness of this consideration requires the calculations in the space
by the corresponding topology (see, e. g.,[16]). Strictly speaking, the mathematical correctness of this consideration requires the calculations in the space 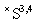 of the generalized functions, i. e. with the application of a cumbersome functional analysis, to be made.Nevertheless, let us take into account that the Schwartz test function space
of the generalized functions, i. e. with the application of a cumbersome functional analysis, to be made.Nevertheless, let us take into account that the Schwartz test function space 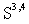 in the triple (7) is kernel. This means that
in the triple (7) is kernel. This means that 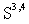 is dense both in the quantum-mechanical space
is dense both in the quantum-mechanical space 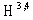 and in the space of generalized functions
and in the space of generalized functions 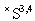 . Therefore, any physical state from
. Therefore, any physical state from 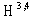 can be approximated with an arbitrary precision by the corresponding elements of the Cauchy sequence in
can be approximated with an arbitrary precision by the corresponding elements of the Cauchy sequence in 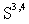 , which converges to the given state in
, which converges to the given state in 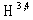 . Further, taking into account the requirement to measure the arbitrary value of the model with non-absolute precision, this means that all necessary calculations can be fulfilled within the Schwartz test function space
. Further, taking into account the requirement to measure the arbitrary value of the model with non-absolute precision, this means that all necessary calculations can be fulfilled within the Schwartz test function space 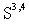 without any loss of generality.Thus, we use below the Schwartz test function space
without any loss of generality.Thus, we use below the Schwartz test function space 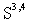 .
.3. Lagrangian for the Free Spinor Field in the Foldy–Wouthuysen Representation
- Now therefore, the FW equation for the vectors
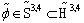 has the form
has the form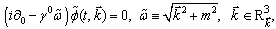 | (10) |
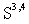 , as well as the rigged Hilbert space, is invariant with respect to the Fourier transformation. The complete analogy with the classical mechanics is as follows. The FW equation (10) is the first-order differential equation with respect to the time parameter t and continually infinite system of the algebraic equations with respect to the numerical dynamical variables
, as well as the rigged Hilbert space, is invariant with respect to the Fourier transformation. The complete analogy with the classical mechanics is as follows. The FW equation (10) is the first-order differential equation with respect to the time parameter t and continually infinite system of the algebraic equations with respect to the numerical dynamical variables 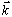 .Therefore, we consider the 4-component field
.Therefore, we consider the 4-component field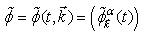 | (11) |
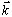 and discrete number of components with respect to the variables
and discrete number of components with respect to the variables 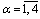 . Therefore, we construct the Lagrange function in the terms of corresponding numerical numbers in the form
. Therefore, we construct the Lagrange function in the terms of corresponding numerical numbers in the form 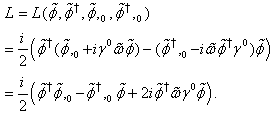 | (12) |
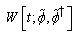 from the functions
from the functions 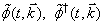 and from the numerical variable
and from the numerical variable 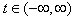 ) is given by
) is given by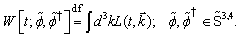 | (13) |
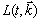 is found from the prime Lagrangian (12) by substituting the functions
is found from the prime Lagrangian (12) by substituting the functions 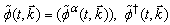 and their time-derivatives
and their time-derivatives 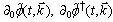 belonging to the
belonging to the 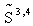 , instead of the numerical variables
, instead of the numerical variables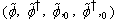 , respectively.It is easy to verify that for the action (13) the Euler–Lagrange equations
, respectively.It is easy to verify that for the action (13) the Euler–Lagrange equations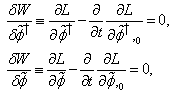 | (14) |
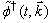 .The Lagrange approach in any other realization of the space
.The Lagrange approach in any other realization of the space 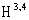 , which is related to the complete set of the dynamical variables in
, which is related to the complete set of the dynamical variables in 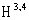 as the diagonal operators, is constructed similarly. For example, in the
as the diagonal operators, is constructed similarly. For example, in the 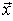 -realization of the space
-realization of the space 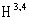 the corresponding Lagrangian and action are given by
the corresponding Lagrangian and action are given by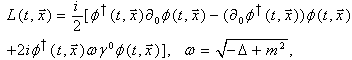 | (15) |
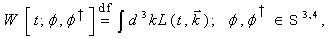 | (16) |
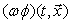 (the result of the action of the pseudo-differential operator
(the result of the action of the pseudo-differential operator 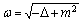 on the function
on the function 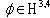 ) is determined by the formula
) is determined by the formula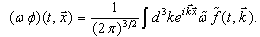 | (17) |
 , etc. In other words, the time t plays a specific isolated role in all the expressions and formulae (in the formula (13) as well). The time t is the parameter in all canonical FW-like models (see, e.g., [17, 18] for more details). Nevertheless, the Lagrange approach under consideration is the relativistic invariant in the following sense. The set
, etc. In other words, the time t plays a specific isolated role in all the expressions and formulae (in the formula (13) as well). The time t is the parameter in all canonical FW-like models (see, e.g., [17, 18] for more details). Nevertheless, the Lagrange approach under consideration is the relativistic invariant in the following sense. The set 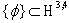 of extremals for the action (14) (the set
of extremals for the action (14) (the set 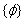 of solutions
of solutions 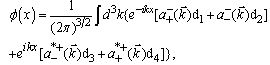 | (18) |
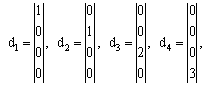 | (19) |
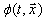 ), which coincide with the FW equation
), which coincide with the FW equation 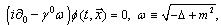 | (20) |
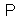 -invariant. In more detail, the set
-invariant. In more detail, the set 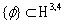 is invariant with respect to the unitary in the
is invariant with respect to the unitary in the 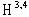 representation of the group
representation of the group 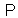 determined by the Hermitian
determined by the Hermitian 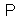 -generators
-generators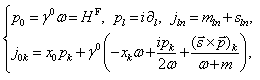 | (21) |
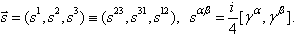 | (22) |
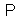 -invariance of the canonical FW-like models are considered in[17, 18].In solution (18), the coefficients
-invariance of the canonical FW-like models are considered in[17, 18].In solution (18), the coefficients 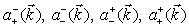 are the quantum-mechanical momentum-spin amplitudes, i. e. the amplitudes of probability distribution over the eigen values of the fermionic Hermitian stationary complete set of operators of the momentum
are the quantum-mechanical momentum-spin amplitudes, i. e. the amplitudes of probability distribution over the eigen values of the fermionic Hermitian stationary complete set of operators of the momentum 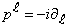 spin projection
spin projection 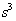 and sign of the charge
and sign of the charge 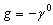 . In
. In 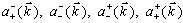 , the lower indices are the signs of the spin projections and the upper indices are those of the sign of the charge, respectively.Remark 3.1. In the above mentioned stationary complete set of operators
, the lower indices are the signs of the spin projections and the upper indices are those of the sign of the charge, respectively.Remark 3.1. In the above mentioned stationary complete set of operators 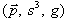 the spin projection operator is chosen in the representation
the spin projection operator is chosen in the representation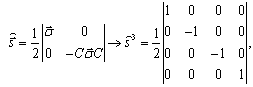 | (23) |
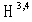 .
. 4. Dynamical Invariants of the Spinor Field in the Foldy–Wouthuysen Representation
- The Noether theorem for an arbitrary Hermitian operator q of invariance of equation (20) gives the following general formula of deriving the conservation law Q(t)=Const:
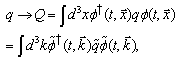 | (24) |
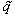 is the Fourier transform in
is the Fourier transform in 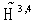 of the operator q from
of the operator q from 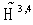 . The Noether formula (24) coincides with that for the mean value in
. The Noether formula (24) coincides with that for the mean value in 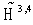 (or in
(or in 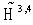 ) of an arbitrary observable q from the algebra of observables. The details of the application of the Noether theorem for the spinor field can be found in[19].Thus, in order to find the main conservation laws for the spinor field in the FW representation, it is sufficient to substitute the 10 generators
) of an arbitrary observable q from the algebra of observables. The details of the application of the Noether theorem for the spinor field can be found in[19].Thus, in order to find the main conservation laws for the spinor field in the FW representation, it is sufficient to substitute the 10 generators 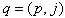 (21), together with the solutions (18), in the formula (24) and to fullfil the necessary calculations. Note that, contrary to the
(21), together with the solutions (18), in the formula (24) and to fullfil the necessary calculations. Note that, contrary to the 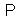 -generators
-generators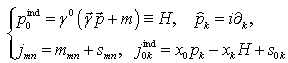 | (25) |
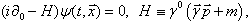 | (26) |
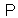 -representation (i. e. in the Pauli – Dirac representation), for the
-representation (i. e. in the Pauli – Dirac representation), for the 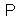 -generators (21) in the FW representation,
-generators (21) in the FW representation, 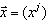 is the natural coordinate and
is the natural coordinate and 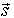 (22) is the natural spin. Therefore, each element from the set of generators (21) has the natural physical sense. In the FW representation, the spin
(22) is the natural spin. Therefore, each element from the set of generators (21) has the natural physical sense. In the FW representation, the spin 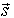 (22) commutes with the operator of the FW equation (20) and is conserved. The orbital angular momentum is conserved as well. It is also valid both for the space angular momentum and for the proper Lorentz momentum (boost). Therefore, here we have additional, as compared to the Dirac theory, conservation laws
(22) commutes with the operator of the FW equation (20) and is conserved. The orbital angular momentum is conserved as well. It is also valid both for the space angular momentum and for the proper Lorentz momentum (boost). Therefore, here we have additional, as compared to the Dirac theory, conservation laws 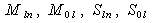 of the orbital and spin parts of the total Poincaré angular momentum.Remark 4.1. Strictly speaking, the 12 conservation laws
of the orbital and spin parts of the total Poincaré angular momentum.Remark 4.1. Strictly speaking, the 12 conservation laws 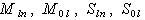 can be found on the basis of two methods. For the Dirac theory (i. e. in the Pauli – Dirac representation), these conservation laws can be found as well. Nevertheless, in the Pauli – Dirac representation, the corresponding symmetry generators
can be found on the basis of two methods. For the Dirac theory (i. e. in the Pauli – Dirac representation), these conservation laws can be found as well. Nevertheless, in the Pauli – Dirac representation, the corresponding symmetry generators 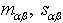 are nonlocal and are given by much more cumbersome expressions, see, e. g., expression
are nonlocal and are given by much more cumbersome expressions, see, e. g., expression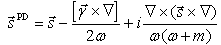 | (27) |
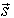 (22), which commutes with the operator of the FW equation (20), has much simpler and more attractive form. Moreover, consideration in the FW representation in the rigorous canonical quantum mechanical principles and conceptions is given. Therefore, below we consider the dynamical variables for the spinor field in the canonical FW representation.According to the Noether formula (24), the 10 main conservation laws for the spinor field, which are the consequences of the
(22), which commutes with the operator of the FW equation (20), has much simpler and more attractive form. Moreover, consideration in the FW representation in the rigorous canonical quantum mechanical principles and conceptions is given. Therefore, below we consider the dynamical variables for the spinor field in the canonical FW representation.According to the Noether formula (24), the 10 main conservation laws for the spinor field, which are the consequences of the 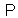 -symmetry (21) of the FW equation (20), i. e., the consequences of the generators
-symmetry (21) of the FW equation (20), i. e., the consequences of the generators 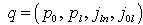 (21), have the form
(21), have the form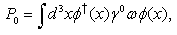 | (28) |
 | (29) |
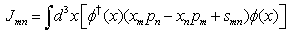 | (30) |
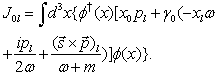 | (31) |
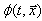 is evolved.Note that the conserved quantities (30) and (31) are the sums of quantities which are conserved itself. They are the sums of the orbital and spin angular momenta. Therefore, we have 12 additional conservation laws:
is evolved.Note that the conserved quantities (30) and (31) are the sums of quantities which are conserved itself. They are the sums of the orbital and spin angular momenta. Therefore, we have 12 additional conservation laws: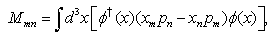 | (32) |
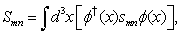 | (33) |
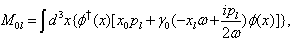 | (34) |
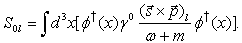 | (35) |
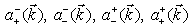 , which determine the general solution (18) of the FW equation (20), i. e. in the terms of quantum-mechanical particle-antiparticle (electron-positron) amplitudes.The following theorem is valid.Theorem 4.1. In the terms of the momentum-spin amplitudes
, which determine the general solution (18) of the FW equation (20), i. e. in the terms of quantum-mechanical particle-antiparticle (electron-positron) amplitudes.The following theorem is valid.Theorem 4.1. In the terms of the momentum-spin amplitudes 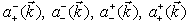 the conservation laws (28)–(31) have the form
the conservation laws (28)–(31) have the form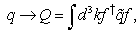 | (36) |
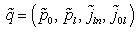 , which act on the momentum-spin amplitudes
, which act on the momentum-spin amplitudes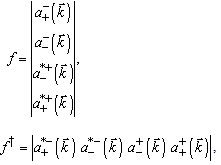 | (37) |
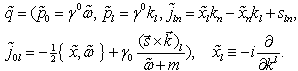 | (38) |
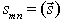 are known from (22). The similar form (36) for the additional conservation laws (32)–(35) is also valid. The operators
are known from (22). The similar form (36) for the additional conservation laws (32)–(35) is also valid. The operators  (38) as well as the operators
(38) as well as the operators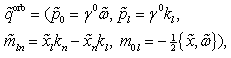 | (39) |
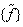 and satisfy the commutation relations
and satisfy the commutation relations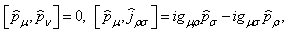 | (40) |
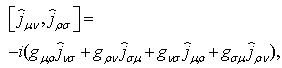 | (41) |
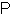 in the manifestly covariant form.Proof. The proof of the theorem is performed by the direct calculations of all necessary expressions and commutation relations.Therefore, the list of the 22 conservation laws (10 principal Poincaré conserved quantities and 12 additional ones) in terms of the quantum-mechanical momentum-spin amplitudes is given by
in the manifestly covariant form.Proof. The proof of the theorem is performed by the direct calculations of all necessary expressions and commutation relations.Therefore, the list of the 22 conservation laws (10 principal Poincaré conserved quantities and 12 additional ones) in terms of the quantum-mechanical momentum-spin amplitudes is given by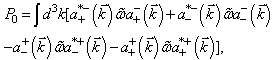 | (42) |
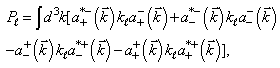 | (43) |
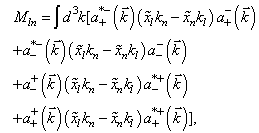 | (44) |
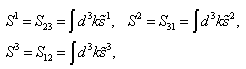 | (45) |
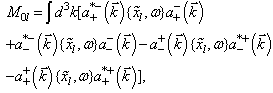 | (46) |
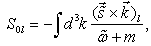 | (47) |
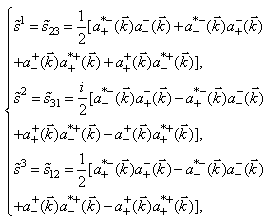 | (48) |
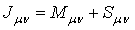 | (49) |
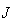 (49) is the sum of the orbital and spin parts, each of them being conserved itself.Note that this list of conserved quantities essentially differs from that given by[10] and by the authors of other publications on the subject, where the Dirac equation has been used. The difference is in conservation of the angular and spin quantities itself.The expressions for the conservation laws for the particle doublet given above can be easily separated into the quantities for a particle and an antiparticle. Therefore, above we have also found the conservation laws for a single fermion (and a single antifermion).The list of the principal conservation laws given above is not complete without the conserved quantities of field charge and the number of particles. Therefore, below we consider these conserved quantities as well.We present the current in the FW representation by analogy with the current
(49) is the sum of the orbital and spin parts, each of them being conserved itself.Note that this list of conserved quantities essentially differs from that given by[10] and by the authors of other publications on the subject, where the Dirac equation has been used. The difference is in conservation of the angular and spin quantities itself.The expressions for the conservation laws for the particle doublet given above can be easily separated into the quantities for a particle and an antiparticle. Therefore, above we have also found the conservation laws for a single fermion (and a single antifermion).The list of the principal conservation laws given above is not complete without the conserved quantities of field charge and the number of particles. Therefore, below we consider these conserved quantities as well.We present the current in the FW representation by analogy with the current 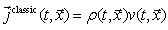 in the theory of a continuous medium. Taking into account that the velocity operator in the FW representation is given by
in the theory of a continuous medium. Taking into account that the velocity operator in the FW representation is given by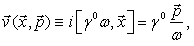 | (50) |
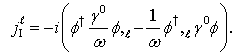 | (51) |
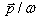 is also some velocity. Therefore, in addition to (51) we have here another current vector
is also some velocity. Therefore, in addition to (51) we have here another current vector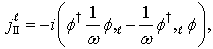 | (52) |
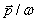 .It is easy to show that 4-currents, which correspond to the current vectors (51), (52), obey the continuity equation
.It is easy to show that 4-currents, which correspond to the current vectors (51), (52), obey the continuity equation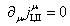 | (53) |
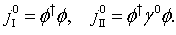 | (54) |
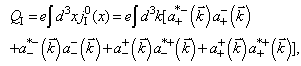 | (55) |
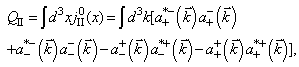 | (56) |
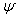 into the FW equation (20) and its solution
into the FW equation (20) and its solution 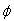 (18) (and vice versa), gives
(18) (and vice versa), gives 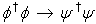 , i.e. does not change the charge conservation law. Moreover, in the momentum representation in the terms of momentum-spin amplitudes, the FW and the Dirac conservation laws for the spinor field coincide between each other. The difference is in the procedure of their Noether calculation. In the Pauli – Dirac representation, where the symmetry operators of the orbital angular momentum and spin are much more cumbersome, this procedure is also much more cumbersome. It is evident from the comparison of the corresponding spin operators (22) and (27).
, i.e. does not change the charge conservation law. Moreover, in the momentum representation in the terms of momentum-spin amplitudes, the FW and the Dirac conservation laws for the spinor field coincide between each other. The difference is in the procedure of their Noether calculation. In the Pauli – Dirac representation, where the symmetry operators of the orbital angular momentum and spin are much more cumbersome, this procedure is also much more cumbersome. It is evident from the comparison of the corresponding spin operators (22) and (27).5. The Fermi-Quantization
- In general, the procedure of quantization for the spinor field in the FW representation is similar to that in the standard Pauli – Dirac representation. The procedure is carried out by the standard canonical way, i.e. by applying the proposed Lagrangian (15), the field coordinate and the canonically conjugated field momentum. The requariements of the anticommutation relations for these canonically conjugated variables are reduced to the replacement of the quantum-mechanical amplitudes
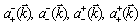 in the general solution (18) by the operators
in the general solution (18) by the operators 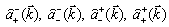 obeying the Fermi anticommutation relations. These operators determine the basis vectors in the Fock space
obeying the Fermi anticommutation relations. These operators determine the basis vectors in the Fock space 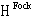 of the quantized field
of the quantized field 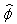 . After such replacement and redefinition as the normal products, the expressions
. After such replacement and redefinition as the normal products, the expressions 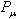 (42), (43) and
(42), (43) and 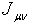 (49) are transformed into the
(49) are transformed into the 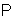 -generators
-generators 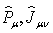 of the Lie algebra of the group
of the Lie algebra of the group 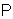 in the Fock space
in the Fock space 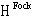 . The
. The 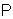 -generators
-generators 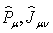 in this space obey the manifestly covariant commutation relations (40), (41) and realize the unitary
in this space obey the manifestly covariant commutation relations (40), (41) and realize the unitary 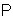 -representation.The operator of energy
-representation.The operator of energy 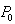 (42) becomes sign-determined
(42) becomes sign-determined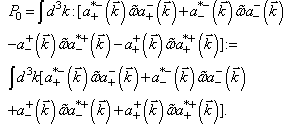 | (57) |
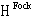 of the fermion-antifermion field
of the fermion-antifermion field 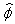 , the energy of the quantized spinor field is positive.After the Fermi-quantization, the conserved quantities (55), (56) also become the operators in the space
, the energy of the quantized spinor field is positive.After the Fermi-quantization, the conserved quantities (55), (56) also become the operators in the space 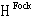 and are given by
and are given by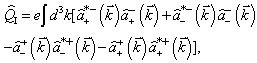 | (58) |
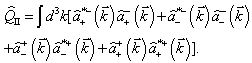 | (59) |
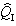 is the operator of charge and
is the operator of charge and 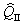 is the operator of particle number.Note that despite the non-covariant procedure of the field
is the operator of particle number.Note that despite the non-covariant procedure of the field 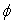 quantization, the resulting formalism of the quantized field
quantization, the resulting formalism of the quantized field 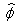 is covariant and effectively coincides with the Wightman’s axiomatic formulation of the quantized spinor field theory (for the modern consideration see, e. g.,[20]).
is covariant and effectively coincides with the Wightman’s axiomatic formulation of the quantized spinor field theory (for the modern consideration see, e. g.,[20]).6. Conclusions
- A new Lagrangian, for which the Euler–Lagrange equations and the standard variational least action principle lead to the Foldy–Wouthuysen equation, is suggested. The extended list of 24 conservation laws is found on the basis of the Noether theorem and the suggested Lagrangian.Thus, we presented the new Lagrange approach for the free spinor field in the Foldy–Wouthuysen representation. We hope that our consideration of the main conservation laws for the free spinor field (in the framework of the Lagrange approach and on the basis of the Noether theorem) is more complete and consistent then the similar considerations of other authors. Our advantage lies in the start from the canonical Foldy–Wouthuysen representation.The construction of the Lagrange approach and the Noether analysis of the field
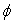 dynamical invariants is the first necessary step towards the construction of the quantum electrodynamics in the Foldy–Wouthuysen representation. The version of such quantum electrodynamics, which used the 8-component formalism and appealed to the negative mass of the antiparticle, was suggested recently in[12]. On the basis of the results considered above and in[6, 18] we are starting with the new approach for the quantum electrodynamics in the Foldy–Wouthuysen representation.Contrary to the consideration of[7, 8], we are based on the standard variational formulation of the least action principle and mathematically well-defined definition of the nonlocal (pseudodifferential) operator
dynamical invariants is the first necessary step towards the construction of the quantum electrodynamics in the Foldy–Wouthuysen representation. The version of such quantum electrodynamics, which used the 8-component formalism and appealed to the negative mass of the antiparticle, was suggested recently in[12]. On the basis of the results considered above and in[6, 18] we are starting with the new approach for the quantum electrodynamics in the Foldy–Wouthuysen representation.Contrary to the consideration of[7, 8], we are based on the standard variational formulation of the least action principle and mathematically well-defined definition of the nonlocal (pseudodifferential) operator 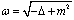 and its functions. We consider such operators as integral and well-defined in the Schwartz space
and its functions. We consider such operators as integral and well-defined in the Schwartz space 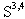 .
. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML