-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2013; 3(2): 73-80
doi:10.5923/j.ijtmp.20130302.04
Proper Curvature Collineations in Non - Static Spatially Homogeneous Rotating Spacetimes by using Lorentzian Metric
M. Ramzan, S. Manzoor, M. S. Shabbir
Department of Mathematics, The Islamia University of Bahawalpur, Bahawalpur, 63100, Pakistan
Correspondence to: M. Ramzan, Department of Mathematics, The Islamia University of Bahawalpur, Bahawalpur, 63100, Pakistan.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this paper we have investigated the curvature collineations of non- static spatially homogeneous rotating spacetimes by using the rank of 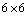 Riemann matrix and direct integration techniques. The above investigation reveals that there are thirty two cases in which the non-static spatially homogeneous rotating spacetimes admits the proper curvature collineations. It is also found that when the above spacetimes admit proper curvature collineations they form an infinite dimensional vector space.
Riemann matrix and direct integration techniques. The above investigation reveals that there are thirty two cases in which the non-static spatially homogeneous rotating spacetimes admits the proper curvature collineations. It is also found that when the above spacetimes admit proper curvature collineations they form an infinite dimensional vector space.
Keywords: Riemann Curvature Tensor, Curvature Collineations, Bivectors, Infinite Dimensional Vector Space
Cite this paper: M. Ramzan, S. Manzoor, M. S. Shabbir, Proper Curvature Collineations in Non - Static Spatially Homogeneous Rotating Spacetimes by using Lorentzian Metric, International Journal of Theoretical and Mathematical Physics, Vol. 3 No. 2, 2013, pp. 73-80. doi: 10.5923/j.ijtmp.20130302.04.
Article Outline
1. Introduction
- The general theory of relativity is the final form of an elegant restructuring of classical mechanics; it is basically the theory of gravitation, which is described by Einstein field equations. The Einstein field equations are, in general, second order highly non-linear partial differential equations. Symmetry restriction on the spacetime metric is a way to find the exact solution of Einstein field equations[9]. It is found that the existence of certain geometric symmetries which are definable in terms of Lie derivatives lead to conservation laws[13]. These symmetries can be expressed in terms of Killing vector fields (KVF), homothetic vector fields (HVF), Ricci collineations (RCS) and Curvature collineations (CCS).Einstein’s theory of relativity tells us that the space and time are all parts of a single physical entity, spacetime continuum. The aim of this paper is to investigate the existence of proper curvature collineations in non static rotating spatially homogeneous spacetime. Spatially homogeneous spacetime posses a group of isometries whose orbits are spacelike hypersurfaces which foliate the spacetime[23]. A spacetime is called static if it is stationary and timelike Killing vector field is orthogonal to the hypersurface, otherwise the spacetime is said to be non-static[24]. The curvature collineations, in general relativity, signifies not only the geometrical symmetry of spacetime, but also implies that the gravitational properties of the field are preserved along the curvature collineations vector[1]. It is therefore important to study the curvature collineations. Katzin et al lead the way for carrying out the detailed study of CCS[1]. G. S.Hall and J. da. Costa provide a systematic way for finding the CCS[5,6]. The proper curvature collineations in various non-static spacetimes has been comprehensively discussed by M. Ramzan.[14]. Different approaches[1-19] are used to study the curvature collineations, but here we shall make use of rank of
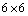 Riemann matrix.Let
Riemann matrix.Let 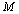 be a four dimensional connected Hausdorff manifold with Lorentz metric
be a four dimensional connected Hausdorff manifold with Lorentz metric 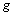 of signature
of signature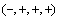 . The components of the curvature tensor associated with the metric
. The components of the curvature tensor associated with the metric 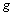 through Levi- Civita connection are denoted by
through Levi- Civita connection are denoted by 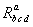 .The covariant derivative, partial derivative and Lie derivative are denoted by a semi-colon, a comma and
.The covariant derivative, partial derivative and Lie derivative are denoted by a semi-colon, a comma and 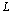 respectively. Round and square brackets denotes the usual symmetrization and anti-symmetrization respectively.The covariant derivative of a differentiable global vector field X on M can be decomposed as
respectively. Round and square brackets denotes the usual symmetrization and anti-symmetrization respectively.The covariant derivative of a differentiable global vector field X on M can be decomposed as 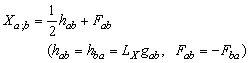 | (1) |
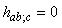 , then X is affine (proper affine if
, then X is affine (proper affine if 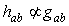 ). If X is affine and
). If X is affine and 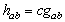 , with c is a constant, then X is called homothetic (proper homothetic if
, with c is a constant, then X is called homothetic (proper homothetic if 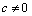 and Killing if
and Killing if 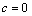 ). A vector field X is said to be curvature collineations if
). A vector field X is said to be curvature collineations if 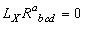 | (2) |
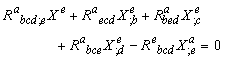 Finally, X is said to be proper curvature collineations if it is not affine[6].
Finally, X is said to be proper curvature collineations if it is not affine[6].2. Classification of Riemann Curvature Tensor
- In this section we shall present the classification of Riemann curvature tensor in terms of its rank and bivector decomposition. The rank of the Riemann tensor can be regarded as the rank of a
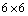 symmetric matrix, derived in a well known way[6]. The rank of the Riemann tensor is the rank of the linear map
symmetric matrix, derived in a well known way[6]. The rank of the Riemann tensor is the rank of the linear map 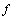 which maps the vector space of all bivectors
which maps the vector space of all bivectors 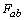 at
at 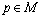 to itself defined byDefine the subspace
to itself defined byDefine the subspace 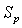 of the tangent space
of the tangent space 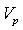 consisting of those members
consisting of those members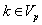 , which satisfy the relation
, which satisfy the relation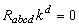 | (3) |
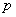 is known to satisfy exactly one of the following conditions[6].Class BThe rank is 2 and the range of
is known to satisfy exactly one of the following conditions[6].Class BThe rank is 2 and the range of 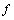 is spanned by the dual pair of non-null simple bivectors and dim
is spanned by the dual pair of non-null simple bivectors and dim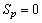 . The Riemann tensor at
. The Riemann tensor at  takes the form
takes the form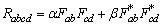 | (4) |
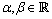 and
and 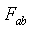 and its dual
and its dual 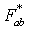 are the unique (upto scaling) simple non-null spacelike and timelike bivectors in the range of
are the unique (upto scaling) simple non-null spacelike and timelike bivectors in the range of 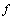 respectively.Class C The rank is 2 or 3 and there exist a unique (up to scaling) solution say
respectively.Class C The rank is 2 or 3 and there exist a unique (up to scaling) solution say 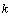 of (3) (and so
of (3) (and so 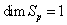 ). The Riemann tensor at point
). The Riemann tensor at point 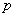 takes the form
takes the form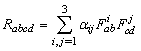 | (5) |
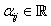 for all
for all 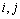 and
and 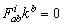 for each of the bivectors
for each of the bivectors 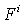 which span the range of
which span the range of 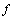 . Class D Here the rank of the curvature matrix is 1. The range of the map
. Class D Here the rank of the curvature matrix is 1. The range of the map 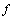 is spanned by a single bivector
is spanned by a single bivector 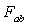 , say, which has to be simple because the symmetry of the Riemann tensor
, say, which has to be simple because the symmetry of the Riemann tensor 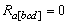 means
means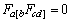 which, together with a standard result implies that
which, together with a standard result implies that 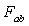 is simple. The curvature tensor admits exactly two independent solutions
is simple. The curvature tensor admits exactly two independent solutions 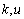 of (3) so that
of (3) so that 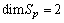 . The Riemann tensor at
. The Riemann tensor at 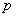 takes the form
takes the form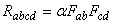 | (6) |
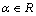 and
and 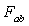 is a simple bivector with blade orthogonal to
is a simple bivector with blade orthogonal to 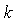 and
and 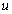 .Class O The rank of the curvature matrix is 0 (so that
.Class O The rank of the curvature matrix is 0 (so that 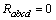 ) and
) and 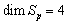 (which is the trivial case)Class A The Riemann tensor is said to b of class A at
(which is the trivial case)Class A The Riemann tensor is said to b of class A at 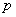 if it is not of class B, C, D or O. Here always
if it is not of class B, C, D or O. Here always 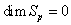 .
.3. Main Results
- Consider the Non-Static Spatially Homogeneous Rotating Spacetime in the cylindrical coordinate system
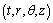 (labeled by
(labeled by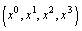 ) with line element[16]
) with line element[16]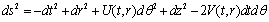 | (7) |
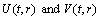 are nowhere zero functions of
are nowhere zero functions of 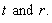 The above spacetime admits two independent Killing vector fields which are:
The above spacetime admits two independent Killing vector fields which are: 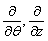 | (8) |
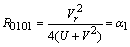
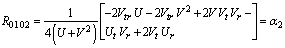
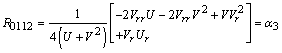
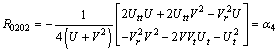
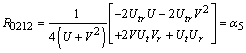
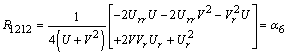 The curvature tensor with components
The curvature tensor with components 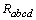 at
at 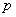 can be written as a
can be written as a 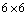 symmetric matrix in a well known way[6]
symmetric matrix in a well known way[6]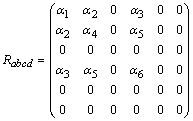 | (9) |
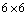 Riemann matrix is less than or equal to three. Since we know from theorem[6] that when the rank of the
Riemann matrix is less than or equal to three. Since we know from theorem[6] that when the rank of the 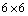 Riemann matrix is greater than three, there exists no proper CCS. There are altogether, forty-one cases for the rank of
Riemann matrix is greater than three, there exists no proper CCS. There are altogether, forty-one cases for the rank of 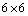 Riemann matrix to be
Riemann matrix to be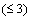 . Since out of six rows of (9) only three rows are non-zero, so only one case for rank 3, three cases for rank 2 and three cases for rank 1 survive. Now suppose the rank of the
. Since out of six rows of (9) only three rows are non-zero, so only one case for rank 3, three cases for rank 2 and three cases for rank 1 survive. Now suppose the rank of the 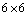 Riemann matrix is three, then there are three non-zero rows or columns in matrix (9). There are fifty six different possible ways for which the rank of the Riemann matrix remains three. Out of which twenty nine yield contradiction and twenty seven survive. For example the case when the rank of
Riemann matrix is three, then there are three non-zero rows or columns in matrix (9). There are fifty six different possible ways for which the rank of the Riemann matrix remains three. Out of which twenty nine yield contradiction and twenty seven survive. For example the case when the rank of 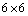 Riemann matrix is three, i.e.
Riemann matrix is three, i.e. 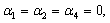 and
and 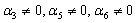 . The constraints imply that
. The constraints imply that 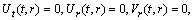 substitution of these information in components of Riemann curvature tensor, we get
substitution of these information in components of Riemann curvature tensor, we get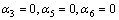 , which gives contradiction because we have assumed that
, which gives contradiction because we have assumed that 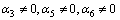 . Therefore, this case is not possible. By similar analysis we have the following surviving possibilities, when the rank of the
. Therefore, this case is not possible. By similar analysis we have the following surviving possibilities, when the rank of the 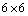 Riemann matrix is three or less. The detail about finding the possibilities for the rank of Riemann matrix to be less than or equal to three can be found in[4]. It is important to note that we are only considering the non static cases, the CCS in the static cases can be found in[25].Thus there exist the following non-static possibilities:(A1)Rank=3,
Riemann matrix is three or less. The detail about finding the possibilities for the rank of Riemann matrix to be less than or equal to three can be found in[4]. It is important to note that we are only considering the non static cases, the CCS in the static cases can be found in[25].Thus there exist the following non-static possibilities:(A1)Rank=3,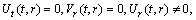
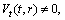
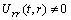 . (A2)Rank=3,
. (A2)Rank=3,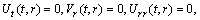
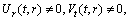 (A3)Rank=3,
(A3)Rank=3, 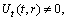
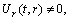
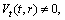
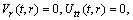
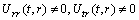
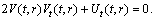 (A4)Rank=3,
(A4)Rank=3, 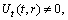
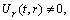
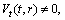
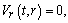
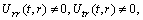
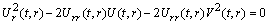 . (A5)Rank=3,
. (A5)Rank=3,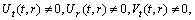
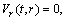
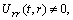
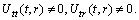 (A6) Rank=3
(A6) Rank=3 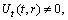
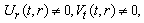
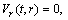
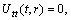
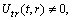 ,
,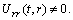 (A7)Rank=3,
(A7)Rank=3,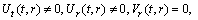
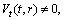
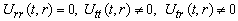 (A8) Rank=3,
(A8) Rank=3,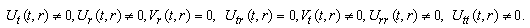 (A9) Rank=3,
(A9) Rank=3, 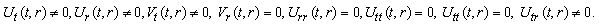 (A10) Rank=3,
(A10) Rank=3,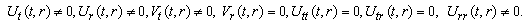 (A11) Rank=3
(A11) Rank=3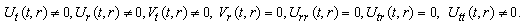 (A12) Rank=3
(A12) Rank=3 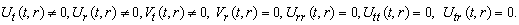 (A13) Rank=3
(A13) Rank=3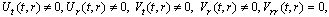
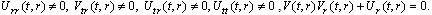 (A14)Rank=3,
(A14)Rank=3, 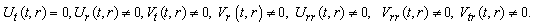 (A15) Rank=3,
(A15) Rank=3, 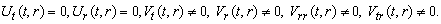 (A16) Rank=3,
(A16) Rank=3, 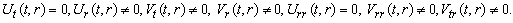 (A17) Rank=3,
(A17) Rank=3, 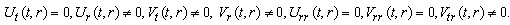 (A18) Rank=3,
(A18) Rank=3, 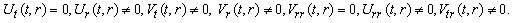 (A19) Rank=3,
(A19) Rank=3, 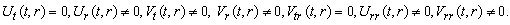 (A20) Rank=3,
(A20) Rank=3, 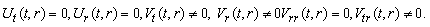 (A21) Rank=3,
(A21) Rank=3, 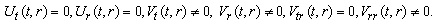 (A22) Rank=3,
(A22) Rank=3, 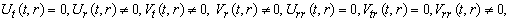 (A23) Rank=3,
(A23) Rank=3, 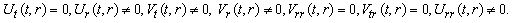 (A24) Rank=3
(A24) Rank=3 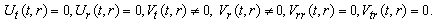 (B1) Rank=2
(B1) Rank=2 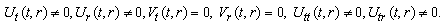 (B2) Rank=2
(B2) Rank=2 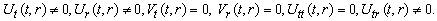 (B3) Rank=2
(B3) Rank=2 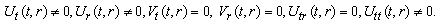 (B4) Rank=2
(B4) Rank=2 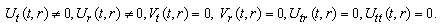 (C1) Rank=1
(C1) Rank=1 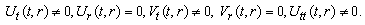 (C2) Rank=1
(C2) Rank=1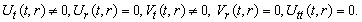 (C3) Rank=1
(C3) Rank=1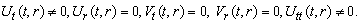 (C4) Rank=1
(C4) Rank=1 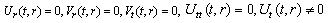
4. Discussion
- It is to be noted that the spacetime (7) is 1+3 decomposable, so all the possible CCS will lie in curvature class C or D.To illustrate the methodology for calculating CCS, we discuss three cases among the thirty two cases.Case A1In this case
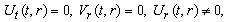
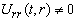 .The above constraint equations imply that
.The above constraint equations imply that 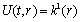 ,
,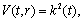 where
where 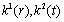 are nowhere zero functions of integration. Here the rank of the Riemann matrix is three and there exists a covariantly constant vector field
are nowhere zero functions of integration. Here the rank of the Riemann matrix is three and there exists a covariantly constant vector field 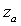 which is a unique solution (up to the multiple) of equation
which is a unique solution (up to the multiple) of equation 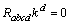 i.e.
i.e. 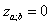 and consequently the Ricci identity implies that
and consequently the Ricci identity implies that 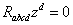 , meaning that
, meaning that 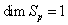 . The line element can be written as:
. The line element can be written as: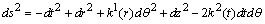 | (10) |
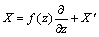 | (11) |
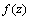 is an arbitrary function of
is an arbitrary function of 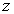 and
and 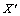 is the homothetic vector field in the induced geometry on each of the three dimensional submanifolds of constant
is the homothetic vector field in the induced geometry on each of the three dimensional submanifolds of constant 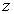 . The completion of this case requires finding the homothetic vector fields in the induced geometry on the submanifolds of constant
. The completion of this case requires finding the homothetic vector fields in the induced geometry on the submanifolds of constant 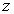 . The induced metric
. The induced metric 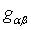 (where
(where 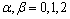 ) has non-zero component given byA vector field
) has non-zero component given byA vector field 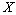 is called homothetic vector field if it satisfies
is called homothetic vector field if it satisfies 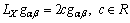 | (13) |
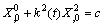 | (14) |
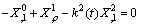 | (15) |
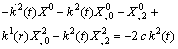 | (16) |
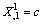 | (17) |
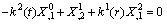 | (18) |
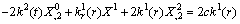 | (19) |
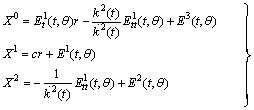 | (20) |
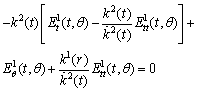 | (21) |
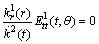 .Since
.Since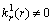 .
. 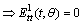 , therefore ,
, therefore , 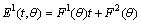 . Using result in (21) and differentiating with respect to‘t’ twice. We get
. Using result in (21) and differentiating with respect to‘t’ twice. We get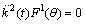 There are three possibilities:
There are three possibilities: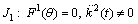
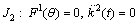
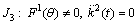 Case
Case 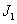 :
: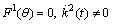 , By backward substitution we get
, By backward substitution we get 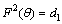 T hus the system (20) becomes
T hus the system (20) becomes 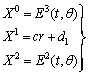 | (22) |
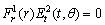 , where
, where 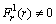
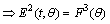 .Consider (14) and using (22) we get,
.Consider (14) and using (22) we get, 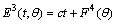 The system (22) takes the form:
The system (22) takes the form: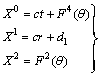 | (23) |
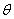 ’ we have ,
’ we have , 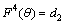 and
and 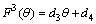 .Equation (23) reduces to:
.Equation (23) reduces to: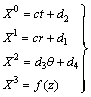 | (24) |
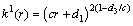 ,
,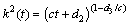 ,
, 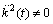 and
and 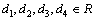 . One can write the proper CCS after subtracting the homothetic vector fields as
. One can write the proper CCS after subtracting the homothetic vector fields as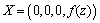 | (25) |
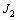 : In this sub case
: In this sub case 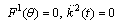
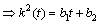 ,Using this information in equation (21) and simplifying we get,
,Using this information in equation (21) and simplifying we get,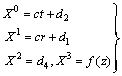 | (26) |
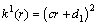 ,
,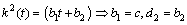 and
and 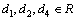 . The proper CCS for this case are given in equation (25).Case
. The proper CCS for this case are given in equation (25).Case 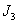 : In this case
: In this case 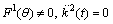 , this sub case gives contradiction because in this case we assume that
, this sub case gives contradiction because in this case we assume that 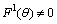 but after straight forward calculation it gives
but after straight forward calculation it gives 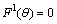 .Cases (A2) to (A24) are precisely same.Case B1In this case we have,
.Cases (A2) to (A24) are precisely same.Case B1In this case we have, 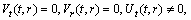
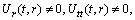
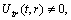 These conditions imply that
These conditions imply that 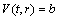 , where
, where 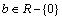 is the constant of integration. Here the rank of the
is the constant of integration. Here the rank of the 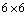 Riemann matrix is two and there exists a spacelike covariantly constant vector field
Riemann matrix is two and there exists a spacelike covariantly constant vector field 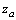 which is a unique solution (up to the multiple) of equation
which is a unique solution (up to the multiple) of equation 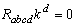 ,
, 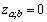 and consequently the Ricci identity implies that
and consequently the Ricci identity implies that 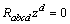 , meaning that
, meaning that 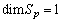 . The line element can be written as:
. The line element can be written as: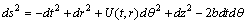 | (27) |
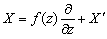 | (28) |
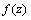 is an arbitrary function of
is an arbitrary function of 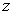 and
and 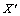 is the homothetic vector field in the induced geometry on each of three dimensional submanifolds of constant
is the homothetic vector field in the induced geometry on each of three dimensional submanifolds of constant 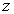 . The completion of this case requires finding the homothetic vector fields in the induced geometry of submanifolds of constant
. The completion of this case requires finding the homothetic vector fields in the induced geometry of submanifolds of constant 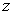 . The induced metric
. The induced metric 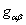 (where
(where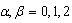 ) has non zero components given by
) has non zero components given by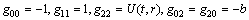 | (29) |
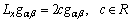 | (30) |
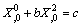 | (31) |
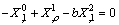 | (32) |
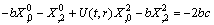 | (33) |
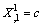 | (34) |
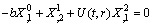 | (35) |
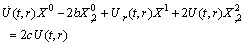 | (36) |
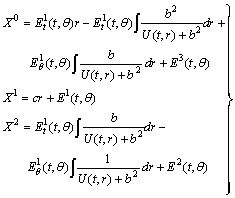 | (37) |
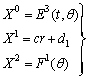 | (38) |
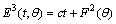 .Thus the system (3.1.121) takes the form
.Thus the system (3.1.121) takes the form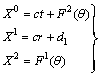 | (39) |
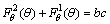
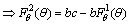
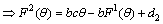 System (39) becomes,
System (39) becomes,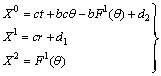 | (40) |
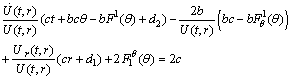 | (41) |
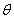 ’, we get
’, we get 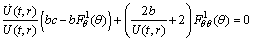 | (42) |
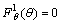 By backward substitution we have the solution:
By backward substitution we have the solution: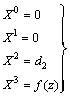 | (43) |
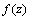 is an arbitrary function of
is an arbitrary function of 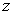 and
and 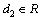 , thus the Killing vector field is of the form
, thus the Killing vector field is of the form 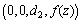 . After subtracting the Killing vectors the CCS can be written as
. After subtracting the Killing vectors the CCS can be written as 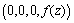 | (44) |
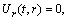
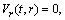
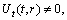
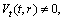
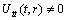 . These conditions imply that
. These conditions imply that 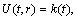
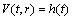 where
where 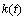 and
and 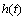 are nowhere zero functions of integration.Here there exists two linearly independent solutions of
are nowhere zero functions of integration.Here there exists two linearly independent solutions of 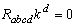 namely
namely 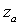 and
and 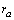 , which are both covariantly constant. This shows that
, which are both covariantly constant. This shows that 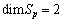 . The line element takes the form
. The line element takes the form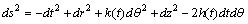 | (45) |
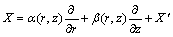 | (46) |
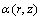 and
and 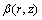 are arbitrary functions of
are arbitrary functions of 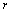 and
and 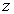 , and
, and 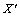 is the curvature collineations in each of the two dimensional submanifolds of constants
is the curvature collineations in each of the two dimensional submanifolds of constants 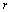 and
and 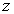 . The procedure for calculating the CCS in the induced geometry on the submanifolds can be seen in[6]. The nonzero components of the induced metric on each of the two-dimensional submanifolds of constant
. The procedure for calculating the CCS in the induced geometry on the submanifolds can be seen in[6]. The nonzero components of the induced metric on each of the two-dimensional submanifolds of constant 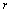 and
and 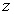 , are given by:
, are given by: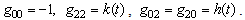 | (47) |
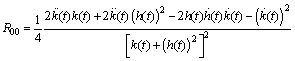
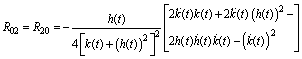
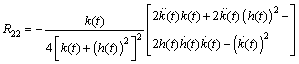 and the Ricci scalar is given by
and the Ricci scalar is given by 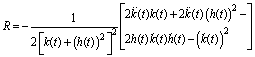 Accordingly, the Einstein tensor
Accordingly, the Einstein tensor 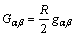 , (where
, (where 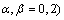 has non zero components
has non zero components 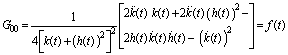 | (48) |
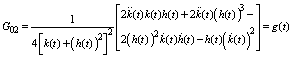 | (49) |
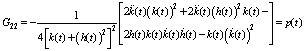 | (50) |
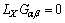 ,by using (48) to (50)
,by using (48) to (50)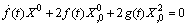 | (51) |
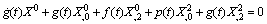 | (52) |
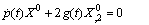 | (53) |
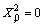 . Otherwise the solution will be trivial.Now by solving (51) and (52), we get:
. Otherwise the solution will be trivial.Now by solving (51) and (52), we get: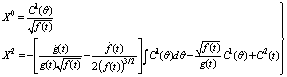 | (54) |
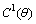 and
and 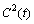 are functions of integration. Proceeding further with equation (54), we get the condition
are functions of integration. Proceeding further with equation (54), we get the condition 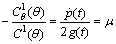 | (55) |
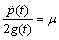 ,(b)
,(b)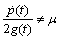 where
where 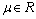 First consider sub case (a), in this case there exists three possibilities which are (i)
First consider sub case (a), in this case there exists three possibilities which are (i)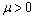 (ii)
(ii)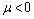 (iii)
(iii)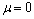 We discuss each possibility in turnCase (a) iIn this case
We discuss each possibility in turnCase (a) iIn this case 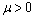 and equation (55) implies that
and equation (55) implies that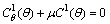 . The solution of the equation is
. The solution of the equation is 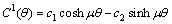 | (56) |
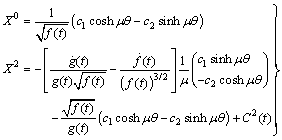 | (57) |
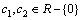 and provided that
and provided that 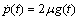 . After subtracting the Killing vector fields, the CCS are
. After subtracting the Killing vector fields, the CCS are 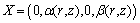 | (58) |
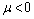 . Put
. Put 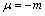 where
where 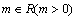 . The CCS in this case are:
. The CCS in this case are: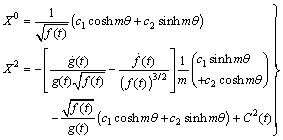 | (59) |
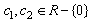 and provided that
and provided that 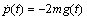 . In this case the proper CCS are given in equation (58).Case (a) iii Here
. In this case the proper CCS are given in equation (58).Case (a) iii Here 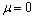 , CCS in this case are
, CCS in this case are 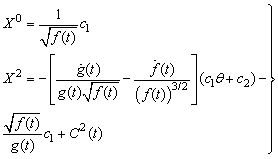 | (60) |
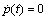 . After subtracting the Killing vector fields the proper CCS are given in equation (58).Case (b) In this case the CCS are
. After subtracting the Killing vector fields the proper CCS are given in equation (58).Case (b) In this case the CCS are 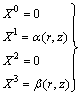 | (61) |
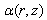 and
and 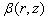 are arbitrary functions of
are arbitrary functions of 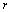 and
and 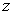 . The proper CCS in this case are given in equation (58).Cases (C2) and (C4) are precisely same.
. The proper CCS in this case are given in equation (58).Cases (C2) and (C4) are precisely same.5. Summary
- In this paper a mathematical study of non-static spatially homogeneous rotating spacetimes according to their proper CCS is presented. An approach developed in[6] is adopted to study the proper CCS of above spacetimes by using the rank of
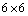 Riemann matrix. From this study we have the following results.a) In the cases (A1) to (A24) rank of the
Riemann matrix. From this study we have the following results.a) In the cases (A1) to (A24) rank of the 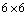 Riemann matrix is three and there exists a unique spacelike covariantly constant vector field which is the solution of equation
Riemann matrix is three and there exists a unique spacelike covariantly constant vector field which is the solution of equation 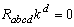 .In these cases the spacetime (7) admits proper CCS which form an infinite dimensional vector space.b) In the cases (B1) to (B4) the rank of the
.In these cases the spacetime (7) admits proper CCS which form an infinite dimensional vector space.b) In the cases (B1) to (B4) the rank of the 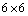 Riemann matrix is two and there exists a unique spacelike covariantly constant vector field which is the solution of equation
Riemann matrix is two and there exists a unique spacelike covariantly constant vector field which is the solution of equation 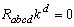 . In these cases the spacetime (7) admits proper CCS which form an infinite dimensional vector space.c) In cases (C1) to (C4) the rank of the
. In these cases the spacetime (7) admits proper CCS which form an infinite dimensional vector space.c) In cases (C1) to (C4) the rank of the 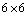 Riemann matrix is one and there exists two independent nowhere zero spacelike covariantly constant vector fields which are the solution of equation
Riemann matrix is one and there exists two independent nowhere zero spacelike covariantly constant vector fields which are the solution of equation 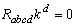 In these cases the spacetime (7) admits proper CCS which again form an infinite dimensional vector space. When we say that CCS forms an infinite dimensional vector space, it actually means that CCS forms an infinite dimensional Lie algebra or Lie groups. Lie groups have fundamental importance in physical system like phase spaces and symmetry groups. When we study the dynamical system with infinite number of degrees of freedom such as PDEs and fields theories, then it is necessary to study the infinite dimensional Lie groups or Lie algebra
In these cases the spacetime (7) admits proper CCS which again form an infinite dimensional vector space. When we say that CCS forms an infinite dimensional vector space, it actually means that CCS forms an infinite dimensional Lie algebra or Lie groups. Lie groups have fundamental importance in physical system like phase spaces and symmetry groups. When we study the dynamical system with infinite number of degrees of freedom such as PDEs and fields theories, then it is necessary to study the infinite dimensional Lie groups or Lie algebraACKNOWLEDGEMENTS
- The first author would like to thank Prof. Ghulam Shabbir (Ghulam Ishaq Khan Institute of Engineering Sciences and Technology, Topi, Swabi, Pakistan) for his help and many useful discussions.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML