-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2013; 3(2): 69-72
doi:10.5923/j.ijtmp.20130302.03
Fuzzy Pairwise L-Open Sets and Fuzzy Pairwise L-Continuous Functions
M. E. Abd El-Monsef1, A. Kozae1, A. A. Salama2, H. M. Elagamy1
1Department of Mathematics, Faculty of Science, Tanta University, Egypt
2Department of Mathematics and Computer Sciences, Faculty of Sciences, Port Said University, Egypt
Correspondence to: M. E. Abd El-Monsef, Department of Mathematics, Faculty of Science, Tanta University, Egypt.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The aim of this paper is to introduce and study some new fuzzy pairwise notion in fuzzy bitopological ideals spaces. We also generalize the notion of fuzzy L-open sets due to Abd El-Monsef et al[1]. In addition to generalize the concept of fuzzy L-closed sets, fuzzy L-continuity and L-open functions due to Abd El-Monsef et al[1]. Relationships between the above new fuzzy pairwise notions and there other relevant classes are investigated. Recently, we define and study two different types of fuzzy pairwise functions.
Keywords: Fuzzy Ideals, Fuzzy Bitopological Spaces, Fuzzy L-open Sets, Fuzzy L-continuous Functions
Cite this paper: M. E. Abd El-Monsef, A. Kozae, A. A. Salama, H. M. Elagamy, Fuzzy Pairwise L-Open Sets and Fuzzy Pairwise L-Continuous Functions, International Journal of Theoretical and Mathematical Physics, Vol. 3 No. 2, 2013, pp. 69-72. doi: 10.5923/j.ijtmp.20130302.03.
Article Outline
1. Introduction
- The concept of fuzzy sets was first introduced by Zadeh[8].Subsequently, Chang defined the notion of fuzzy topology[4]. Since then various aspects of general topology were investigated and. carried out in fuzzy since by several authors of this field. The notions of fuzzy ideal and and fuzzy pairwes local function introduced and studied in[2]. Nouh[6] initiated the study of fuzzy bitopological spaces. A fuzzy set equipped with two fuzzy topologies is called a fuzzy bitopological space. Concepts of fuzzy ideals and fuzzy local function were introduced by Sarkar[7]. The purpose of this paper is to to introduce and study some new pairwise fuzzy notion in fuzzy bitopological ideals spaces. We also generalize the notion of fuzzy L-open sets due to Abd El-Monsef et al[1]. In addition to generalize the concept of L-closed sets, L-continuity and L-open functions due to Abd El-Monsef et al[1].
2. Preliminaries
- Throughout this paper, by
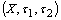 , we mean a fuzzy bitopological space (fbts in short) in Nouh's[6] sense. A fuzzy point in X with support
, we mean a fuzzy bitopological space (fbts in short) in Nouh's[6] sense. A fuzzy point in X with support 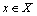 and value
and value 
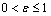 is denoted by
is denoted by 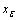 in[3]. A fuzzy point
in[3]. A fuzzy point 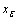 is said to be contained in a fuzzy set
is said to be contained in a fuzzy set 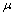 in IX iff
in IX iff 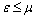 and this will be denoted by
and this will be denoted by 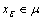 [3]. For a fuzzy set
[3]. For a fuzzy set 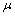 in a fbts
in a fbts 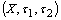 ,
,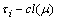 ,
,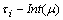 ,
,  , and
, and  will respectively denote closure, interior and complement of
will respectively denote closure, interior and complement of 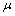 . The constant fuzzy sets taking values 0 and 1 on X are denoted by ox, 1x respectively. A fuzzy set
. The constant fuzzy sets taking values 0 and 1 on X are denoted by ox, 1x respectively. A fuzzy set 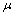 in fts is said to be quasi-coincident[5] with a fuzzy set
in fts is said to be quasi-coincident[5] with a fuzzy set 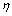 , denoted by
, denoted by  , if there exists
, if there exists  such that
such that 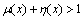 . A fuzzy set
. A fuzzy set 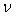 in a fts
in a fts 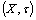 , is called a q-nbd[3,5] of a fuzzy point
, is called a q-nbd[3,5] of a fuzzy point  iff there exists a fuzzy open set
iff there exists a fuzzy open set  such that
such that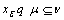 , we will denoted the set of all q-nbd of
, we will denoted the set of all q-nbd of 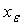 in
in 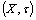 by
by  . A nonempty collection of fuzzy sets L of a set X is called fuzzy ideal[5] on X iff i)
. A nonempty collection of fuzzy sets L of a set X is called fuzzy ideal[5] on X iff i) 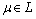 and
and 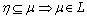 (heredity),(ii)
(heredity),(ii) 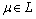 and
and 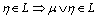 (finite additivity). The fuzzy local function[7]
(finite additivity). The fuzzy local function[7] 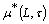 of a fuzzy set
of a fuzzy set 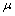 is the union of all fuzzy points
is the union of all fuzzy points  such that if
such that if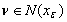 and
and 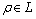 then there is at least one
then there is at least one 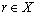 for which
for which 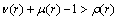 . For a fts (X, ) with fuzzy ideal L,
. For a fts (X, ) with fuzzy ideal L,  [7] for any fuzzy set
[7] for any fuzzy set  of X and
of X and 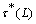 be the fuzzy topology generated by cl*[7].Definition.2.1.[2]. A fuzzy set
be the fuzzy topology generated by cl*[7].Definition.2.1.[2]. A fuzzy set 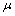 in a fbts
in a fbts 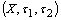 is called pairwise quasi-coincident with a fuzzy set.
is called pairwise quasi-coincident with a fuzzy set. 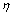 denoted by
denoted by 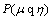 , if there exists
, if there exists  such that
such that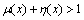 . Obviously, for any two fuzzy sets
. Obviously, for any two fuzzy sets 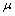 and
and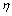 ,
,  will imply
will imply .Definition.2.2.[2]. A fuzzy set
.Definition.2.2.[2]. A fuzzy set 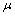 in a fbts) is
in a fbts) is 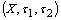 called Pairwise quasi-neighborhood of point
called Pairwise quasi-neighborhood of point  if and only if there exists a fuzzy
if and only if there exists a fuzzy 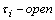 ,
,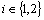 set
set  such that
such that  we will denote the set of all pairwise q-nbd of
we will denote the set of all pairwise q-nbd of 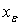 in
in  by
by  ,.
,. Definition 2.3.[2]. Let
Definition 2.3.[2]. Let be a fbts with fuzzy ideal L on X, and
be a fbts with fuzzy ideal L on X, and . Then the fuzzy pairwise local function
. Then the fuzzy pairwise local function 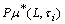 ,
, of
of 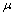 is the union of all fuzzy points
is the union of all fuzzy points 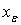 such that for
such that for  and
and 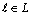 then there is at least one
then there is at least one 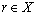 for which
for which 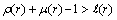 , where
, where 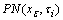 is the set of all q-nbd of
is the set of all q-nbd of 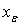 Therefore, any
Therefore, any  ,
, ( for any
( for any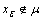 ( any fuzzy set ) implies hereafter,
( any fuzzy set ) implies hereafter, 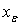 is not contained in the fuzzy set
is not contained in the fuzzy set 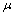 , i.e.
, i.e. 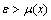 implies there is at least one
implies there is at least one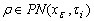 such that for every
such that for every 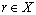 for which
for which 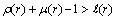 for some
for some 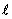 ∈ L. We will occasionally write
∈ L. We will occasionally write  or
or 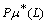 for
for  We define
We define 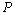 *-fuzzy closure operator, denoted by pcl* for fuzzy topology τ*
*-fuzzy closure operator, denoted by pcl* for fuzzy topology τ*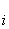 (L) finer than τ
(L) finer than τ as follows:
as follows: 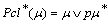 for every fuzzy set
for every fuzzy set 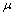 on X. When there is no ambiguity, we will simply write for
on X. When there is no ambiguity, we will simply write for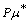 and
and  for
for  and
and 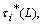 respectively.Definition.2.4.[2]. Let
respectively.Definition.2.4.[2]. Let  be a fbts with fuzzy ideal L on X, a fuzzy pairwise local function
be a fbts with fuzzy ideal L on X, a fuzzy pairwise local function 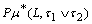 ,
, of
of  is the union of all fuzzy points xε such that for and
is the union of all fuzzy points xε such that for and  then there is at least one
then there is at least one 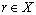 for which
for which , where
, where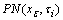 is the set of all q-nbd of
is the set of all q-nbd of  in
in  (where
(where 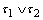 is fuzzy topology generated by
is fuzzy topology generated by 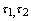 .Example: 2.1.[2]. One may easily verify that If
.Example: 2.1.[2]. One may easily verify that If  then
then 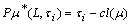 for any
for any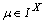 ,
,  .
.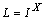 , then
, then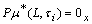 , for any
, for any 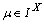 ,
,  .Theorem.2.1.[2]. Let
.Theorem.2.1.[2]. Let 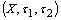 be a fbts with fuzzy ideal L on X,
be a fbts with fuzzy ideal L on X, 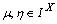 and
and  . Then we have:i)
. Then we have:i) 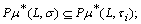
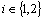 .ii) If
.ii) If  then
then 
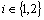 .iii)
.iii) 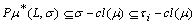 .iv)
.iv) 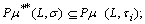
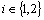 .Theorem.2.2.[2]. Let
.Theorem.2.2.[2]. Let 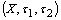 be a fbts with fuzzy ideal L on X,
be a fbts with fuzzy ideal L on X, 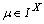 , If
, If 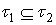 , then i)
, then i) 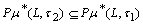 , for every
, for every  ,ii)
,ii) 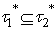 .iii) Cleary
.iii) Cleary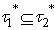 as
as 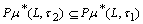 Theorem.2.3.[2]. Let
Theorem.2.3.[2]. Let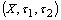 be a fbts and
be a fbts and  be two fuzzy ideals on X. Then for any fuzzy sets
be two fuzzy ideals on X. Then for any fuzzy sets  i.)
i.) 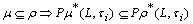 ,
,  .ii.)
.ii.) 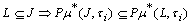 ,
, 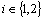 iii)
iii) 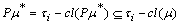 ,
, 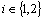 .vi)
.vi) 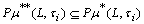
 v)
v) 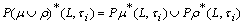 .iv)
.iv) 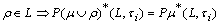
3. On Fuzzy Pairwise Local Function
- Definition.3.1. Given
 be a fbts with fuzzy ideal
be a fbts with fuzzy ideal 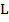 on
on  ,
, 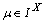 . Then
. Then 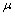 is said to be: i) Fuzzy pairwise
is said to be: i) Fuzzy pairwise  -closed,
-closed, 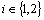 (or PF-*closed) if
(or PF-*closed) if  ii) Fuzzy pairwise PL-dense – in – itself (or PF*-dense- in – itself ) if
ii) Fuzzy pairwise PL-dense – in – itself (or PF*-dense- in – itself ) if 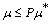 . (iii) Fuzzy pairwise *-perfect if
. (iii) Fuzzy pairwise *-perfect if 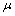 is PF*-closed and PF*-dense – in itself.Theorem.3.1. Given (
is PF*-closed and PF*-dense – in itself.Theorem.3.1. Given ( ,
,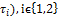 be a fbts with fuzzy ideal
be a fbts with fuzzy ideal 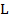 on
on 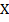 ,
,  then
then 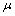 is i) PF*- closed iff cl*(µ) =µ.(ii) PF*- dense – in – itself iff cl*(µ)= pµ*.(iii) PF*- perfect iff cl*(µ)= pµ*=µ.Proof: Follows directly from the fuzzy pairwise closure operator cl* for a fuzzy bitopological
is i) PF*- closed iff cl*(µ) =µ.(ii) PF*- dense – in – itself iff cl*(µ)= pµ*.(iii) PF*- perfect iff cl*(µ)= pµ*=µ.Proof: Follows directly from the fuzzy pairwise closure operator cl* for a fuzzy bitopological  in[2] and Definition 3.1Remark 3.1. One can deduce that (i) Every PF*-dense- in – itself is fuzzy pairwise dense set.(ii) Every fuzzy pairwise closed (resp. fuzzy pairwise open) set is PF*-closed (resp. PF
in[2] and Definition 3.1Remark 3.1. One can deduce that (i) Every PF*-dense- in – itself is fuzzy pairwise dense set.(ii) Every fuzzy pairwise closed (resp. fuzzy pairwise open) set is PF*-closed (resp. PF Corollary.3.1. Given (
Corollary.3.1. Given (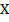 ,
,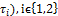 be a fbts with fuzzy ideal
be a fbts with fuzzy ideal 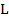 on
on 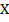 ,
, 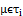 then we have :(i) If µ is PF*-closed then pµ*≤ int(µ) ≤ cl(µ).(ii) If µ is PF*-dense- itself then int(µ)≤ pµ*.(iii) If µ is PF*- perfect then int(µ) = cl(µ) = pµ*.Proof: Obvious.Theorem.3.1. Given
then we have :(i) If µ is PF*-closed then pµ*≤ int(µ) ≤ cl(µ).(ii) If µ is PF*-dense- itself then int(µ)≤ pµ*.(iii) If µ is PF*- perfect then int(µ) = cl(µ) = pµ*.Proof: Obvious.Theorem.3.1. Given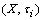 ,
,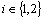 be a fbts with fuzzy ideal
be a fbts with fuzzy ideal 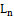 on
on 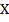 ,
,  then we have the following:(i.)
then we have the following:(i.) 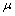 is fuzzy pairwise
is fuzzy pairwise 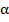 - closed iff µ is PF*- closed.(ii.)
- closed iff µ is PF*- closed.(ii.) 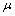 is fuzzy pairwise
is fuzzy pairwise 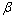 – open iff µ is PF*- dense in itself.(iii.)
– open iff µ is PF*- dense in itself.(iii.) 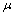 is fuzzy regular pairwise closed iff
is fuzzy regular pairwise closed iff 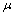 is PF*- perfect.Proof: It ̓s clear.Corollary 3.2. For an fbts
is PF*- perfect.Proof: It ̓s clear.Corollary 3.2. For an fbts 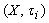 ,
,  with fuzzy ideal
with fuzzy ideal  on
on  ,
, 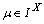 the following holds:(i) If
the following holds:(i) If 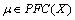 then
then  is PF*- closed.(ii) If
is PF*- closed.(ii) If 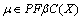 then
then 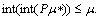 (iii) If
(iii) If then
then 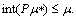 Proof: Obvious.
Proof: Obvious.4. Fuzzy Pairwise L-open and Fuzzy Pairwise L- closed Sets
- Definition.4.1. Given
 ,
,  be a fbts with fuzzy ideal
be a fbts with fuzzy ideal 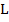 on
on 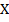 ,
,  and
and 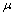 is called a fuzzy pairwise
is called a fuzzy pairwise  -open set iff there exists
-open set iff there exists 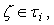
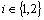 such that
such that 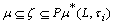
 .We will denote the family of all fuzzy pairwise
.We will denote the family of all fuzzy pairwise  -open on
-open on 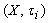
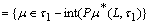 and
and 
 .(simplify
.(simplify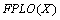 ).When there is no chance for confusion.Theorem.4.1. let
).When there is no chance for confusion.Theorem.4.1. let 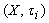 ,
, 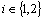 be a fbts with fuzzy ideal L then
be a fbts with fuzzy ideal L then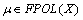 iff
iff 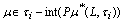 for
for  Proof. Assume that
Proof. Assume that 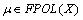 then Definition.4.1. there exists
then Definition.4.1. there exists 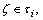 such that
such that 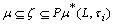 ,
,  . But
. But 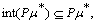 put
put 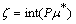 . Hence
. Hence  . Conversely
. Conversely 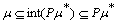 . Then there exists
. Then there exists 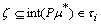 . Hence
. Hence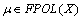 .Definition.4.2.The largest
.Definition.4.2.The largest 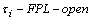 (simply
(simply ) set contained in
) set contained in  is called a
is called a 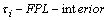 of
of  . The complement of fuzzy pairwise L-open subset of X is a fuzzy pairwise L-closed subset of X (simply FPLC(X)). We denoted by FPL-
. The complement of fuzzy pairwise L-open subset of X is a fuzzy pairwise L-closed subset of X (simply FPLC(X)). We denoted by FPL-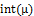 .Theorem.4.2. Let
.Theorem.4.2. Let 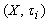 ,
, 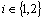 be a fbts with fuzzy ideal L,
be a fbts with fuzzy ideal L, 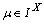 and J is an arbitrary set then i) The union of fuzzy pairwise L-open subsets is fuzzy pairwise L-open.ii) If
and J is an arbitrary set then i) The union of fuzzy pairwise L-open subsets is fuzzy pairwise L-open.ii) If 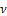 is fuzzy pairwise open and
is fuzzy pairwise open and 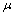 is fuzzy pairwise L-open subset of X. Then
is fuzzy pairwise L-open subset of X. Then  pairwise L-open subset.Proof.i) Let
pairwise L-open subset.Proof.i) Let 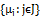 be a family of FPLO(X). Then for each
be a family of FPLO(X). Then for each  and so
and so 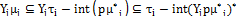 .ii) Assume that
.ii) Assume that  is fuzzy pairwise open and
is fuzzy pairwise open and  is fuzzy pairwise L-open subsets of X. Then
is fuzzy pairwise L-open subsets of X. Then  .Definition.4.3. Let (,
.Definition.4.3. Let (, be a fbts with fuzzy ideal
be a fbts with fuzzy ideal 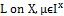 . Then
. Then 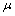 is said to be i) fuzzy
is said to be i) fuzzy 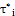 - closed iff
- closed iff 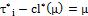 .ii) fuzzy
.ii) fuzzy 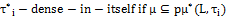 .iii) fuzzy
.iii) fuzzy 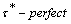 if
if 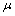 is
is 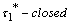 and
and 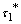 -dense in itself.Theorem.4.3. Given (,
-dense in itself.Theorem.4.3. Given (,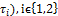 a fbts with fuzzy ideal
a fbts with fuzzy ideal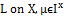 , then the following holds:(i) If
, then the following holds:(i) If 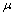 is both fuzzy pairwise L-open and
is both fuzzy pairwise L-open and 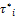 -perfect then
-perfect then 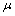 is fuzzy pairwise open.(ii) If
is fuzzy pairwise open.(ii) If 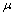 is both fuzzy pairwise open and
is both fuzzy pairwise open and  dense –in – itself then
dense –in – itself then 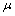 is fuzzy pairwise L-open.Proof. Follows directly from the fuzzy closure operator for and Definition.4.1 Corollary.4.1. For a fuzzy subset
is fuzzy pairwise L-open.Proof. Follows directly from the fuzzy closure operator for and Definition.4.1 Corollary.4.1. For a fuzzy subset 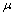 of a fbts
of a fbts 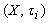 ,
,  with fuzzy ideal , we have:If
with fuzzy ideal , we have:If 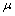 is
is 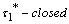 and
and 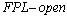 then
then 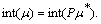 If
If 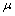 is
is 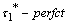 and
and 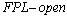 set then
set then  Theorem.4.4. If (,
Theorem.4.4. If (,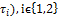 a fbts with fuzzy ideal
a fbts with fuzzy ideal 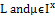 then (i)
then (i)  is fuzzy L-open set.(ii) FPL
is fuzzy L-open set.(ii) FPL iff
iff 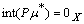 .Proof.(i)Since
.Proof.(i)Since  then
then  Thus
Thus 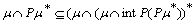
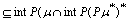 . Hence
. Hence (ii) Let) FPL
(ii) Let) FPL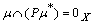 . Then
. Then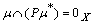 , implies
, implies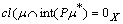 and so
and so  conversely assume that
conversely assume that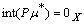 then
then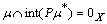 . Hence
. Hence  . Theorem.4.5. If
. Theorem.4.5. If 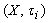 ,
, 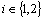 a fbts with fuzzy ideal L on X,
a fbts with fuzzy ideal L on X, 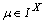 then
then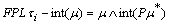 .Proof. Clear Definition.4.4: Given
.Proof. Clear Definition.4.4: Given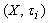 ,
,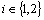 a fbts with fuzzy ideal L and
a fbts with fuzzy ideal L and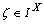 ,
, 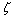 called fuzzy pairwise L-closed set if its complement is fuzzy L-open set. We will denote the family of fuzzy L-closed sets by FPLC(X).Theorem.4.6. Given
called fuzzy pairwise L-closed set if its complement is fuzzy L-open set. We will denote the family of fuzzy L-closed sets by FPLC(X).Theorem.4.6. Given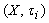 ,
, a fbts with fuzzy ideal L and
a fbts with fuzzy ideal L and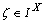 is fuzzy pairwise L-closed set, then
is fuzzy pairwise L-closed set, then 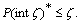 Proof. It’s clear.Theorem.4.7. Given
Proof. It’s clear.Theorem.4.7. Given 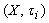 ,
, be a fbts with fuzzy ideal L on X and
be a fbts with fuzzy ideal L on X and 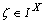 such that
such that  then
then 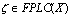 iff
iff  Proof. (Necessity). Follows immedially from the above theorem. (Sufficiency). Let
Proof. (Necessity). Follows immedially from the above theorem. (Sufficiency). Let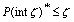 then
then  from the hypothesis. Hence
from the hypothesis. Hence 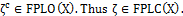 Corollary.4.2. For a fbts
Corollary.4.2. For a fbts  ,
,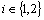 with fuzzy ideal , then the union of fuzzy pairwise L-closed sets is fuzzy pairwise L-closed set.
with fuzzy ideal , then the union of fuzzy pairwise L-closed sets is fuzzy pairwise L-closed set.5. Fuzzy Pairwise L-Continuous Functions
- By utilizing the notion of pairwise L-open sets, we establish in this article a class of fuzzy pairwise L-continuous function. Each of fuzzy pairwise L-continuous and fuzzy pairwise continuous function are independent concepts. Many characterizations and properties of this concept are investigated.Definition.5.1.A fuzzy pairwise function
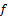 :
: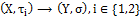 with fuzzy ideal L on X is said to be fuzzy pairwise L-continuous if for every
with fuzzy ideal L on X is said to be fuzzy pairwise L-continuous if for every 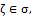
 .Remark.5.1: Every fuzzy pairwise L-continuity is fuzzy pairwise precontinuity but the converse is not true in general as seen by the following example.Example.5.1: Let
.Remark.5.1: Every fuzzy pairwise L-continuity is fuzzy pairwise precontinuity but the converse is not true in general as seen by the following example.Example.5.1: Let 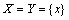 , fuzzy pairwise indiscrete bitopological ,
, fuzzy pairwise indiscrete bitopological , 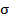 is fuzzy pairwise discrete bitopological and L=
is fuzzy pairwise discrete bitopological and L=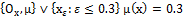 . The fuzzy pairwise identity function
. The fuzzy pairwise identity function 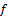 :
: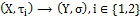 is fuzzy pairwise precontinuous but not fuzzy pairwise L-continuous, since
is fuzzy pairwise precontinuous but not fuzzy pairwise L-continuous, since  while
while  .Theorem.5.1:For a function
.Theorem.5.1:For a function 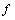 :
: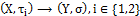 with fuzzy ideal L on X the following are equivalent:(i.)
with fuzzy ideal L on X the following are equivalent:(i.)  is fuzzy pairwise L-continuous.(ii.) For
is fuzzy pairwise L-continuous.(ii.) For 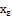 in X and each
in X and each  containing
containing 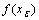 there exists
there exists 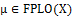 containing
containing 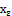 such that
such that  .(iii.) For each fuzzy pairwise point
.(iii.) For each fuzzy pairwise point  in X and
in X and  containing
containing ,
, 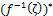 is fuzzy pairwise nbd of
is fuzzy pairwise nbd of 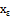 . (iv.) The inverse image of each fuzzy pairwise closed set in Y is fuzzy pairwiseL-closed.Proof: (i.)
. (iv.) The inverse image of each fuzzy pairwise closed set in Y is fuzzy pairwiseL-closed.Proof: (i.)  (ii.). Since
(ii.). Since 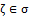 containing,
containing,  then by (i),
then by (i), 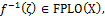 by putting µ=
by putting µ= which containing
which containing 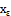 , we have
, we have 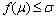 (ii.)
(ii.) 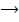 (iii.). Let
(iii.). Let 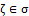 containing
containing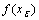 . Then by (ii) there exists containing
. Then by (ii) there exists containing  such that
such that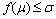 so
so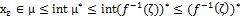 . Hence
. Hence  is fuzzy npbd of
is fuzzy npbd of 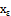 . (iii.)
. (iii.) 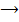 (i.) Let
(i.) Let , since (
, since ( is fuzzy pairwise npbd of any point
is fuzzy pairwise npbd of any point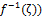 , every point
, every point 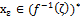 is a fuzzy pairwise interior point of
is a fuzzy pairwise interior point of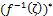 . Then
. Then and hence
and hence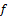 is fuzzy pairwise L-continuous.(i.)
is fuzzy pairwise L-continuous.(i.) 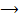 (iv.) Let
(iv.) Let 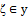 be a fuzzy pairwise closed set. Then
be a fuzzy pairwise closed set. Then 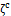 is fuzzy pairwise open set, by
is fuzzy pairwise open set, by  Thus
Thus 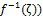 is fuzzy PL-closed set.The following theorem establish the relationship between fuzzy pairwise L-continuous and fuzzy pairwise continuous by using the previous fuzzy pairwise notions.Theorem.5.2. Given
is fuzzy PL-closed set.The following theorem establish the relationship between fuzzy pairwise L-continuous and fuzzy pairwise continuous by using the previous fuzzy pairwise notions.Theorem.5.2. Given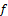 :
: is a function with ideal L on X then we have. If
is a function with ideal L on X then we have. If 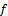 is fuzzy pairwise L-continuous of each fuzzy pairwise*-perfect set in X, then
is fuzzy pairwise L-continuous of each fuzzy pairwise*-perfect set in X, then 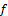 is fuzzy pairwise continuous.Proof: Obvious.Corollary.5.1.Given a function
is fuzzy pairwise continuous.Proof: Obvious.Corollary.5.1.Given a function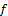 :
: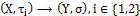 and each member of X is fuzzy pairwise*-dense-in-itself.Then we have:(i.) Every fuzzy pairwise continuous function is fuzzy pairwise L-continuous.(ii.) Each of fuzzy pairwise precontinuous function and fuzzy pairwise L-continuous are equivalent.Proof: It’s clear.
and each member of X is fuzzy pairwise*-dense-in-itself.Then we have:(i.) Every fuzzy pairwise continuous function is fuzzy pairwise L-continuous.(ii.) Each of fuzzy pairwise precontinuous function and fuzzy pairwise L-continuous are equivalent.Proof: It’s clear. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML