-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2013; 3(1): 26-35
doi:10.5923/j.ijtmp.20130301.04
A Strong Contradiction in the Conventional Non-relativistic Theory of the ground State Helium Atom and Helium-like Ions
Viktor D. Ignatiev
Komi science center, Ural Branch of Russian Academy of Sciences, Syktyvkar, Russia
Correspondence to: Viktor D. Ignatiev , Komi science center, Ural Branch of Russian Academy of Sciences, Syktyvkar, Russia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In the conventional theory of the ground state of helium atom, any solution of the two-electron Schrödinger equation is wrong! That is caused by a strong imbalance of proportions of the attraction versus repulsion operators’ acting on a wave function, in the initial differential Schrödinger equation and in its integral algebraic form. In the differential equation, the attraction operators act on the radial part of wave function independently from one another obeying the true proportion: one attraction versus one repulsion per electron. But the resulting wave function turns out to satisfy the wrong integral proportion: two attraction energies versus one repulsion energy per electron. The underlying contradiction is un-coincidence of the additivity rules of energies and energy operators: whereas energies of the electrons may be summed the corresponding energy operators referred to different electrons may not. Consequences of this principal contradiction are discussed.
Keywords: Schrödinger Equation, Attraction/Repulsion Operators, Integration
Cite this paper: Viktor D. Ignatiev , A Strong Contradiction in the Conventional Non-relativistic Theory of the ground State Helium Atom and Helium-like Ions, International Journal of Theoretical and Mathematical Physics, Vol. 3 No. 1, 2013, pp. 26-35. doi: 10.5923/j.ijtmp.20130301.04.
Article Outline
1. Introduction
- Helium atom is the simplest many-electron system. Its theory should be a benchmark of correct approximate description of the electron-electron and electron-nucleus interactions. Agree to common viewpoint the physical grounds of the theory are known exactly and the only problem of interest is a high precision of calculations[1, 2]. Charles Schwartz writes[3]: “For thousands of years mathematicians have enjoyed competing with one another to compute ever more digits of the number π. Among modern physicists, a close analogy is computation of the ground state energy of the Helium atom, begun 75 years ago by E. A. Hylleraas”. Up to date, the total energy is computed with up to 42 decimal digits[4]. In reality, the state of the art of the helium atom problem is not so brilliant at all. In this relation it is important to underline that solution of a Schrödinger equation, first of all, must yield a correct wave function describing just the system under study. We found that the conventional theory of helium atom, invented in 20-30th of the last century contains a substantial contradiction which prevents obtaining the true solution. That contradiction is contradiction between the rules of summing energy operators and energy components. We can and may sum energies of particles. Those are justnumbers. But we may not sum attraction energy operators related to different particles. This principal contradiction leads to many other contradictions and pseudo quantum mechanical misconceptions of the theory. First of them is the next: while the initial Schrödinger equation is formally correct any algebraic equation obtained from it by integration yields substantially wrong radial part of wave function. Section 2 is devoted to a brief description of the conventional theory. In Section 3, the conventional theory is revised. It is demonstrated that 1) integration of the two-electron Schrödinger equation strongly violates true initial proportion of attraction and repulsion operators per electron acting on wave function and 2) Schrödinger equation for one of electrons is free of such a fundamental shortcoming. Corresponding total and orbital energy calculation errors (so named correlation energies) are compared. Section 4 shows an example of advantage of the proposed approach in treating relation between atomic sizes and interatomic distances.
2. Basic Features of the Conventional Non-relativistic Theory of Two-electron Atoms
- Traditionally, the ground-state wave function and energy of helium atom and its isoelectronic ions are obtained by solving the two-electron non-relativistic stationary Schrödinger equation[5– 7]:
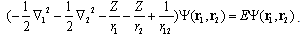 | (1) |
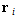 i are the position vectors of electrons, r1 and r2 stand for distances from the first and second electrons to the infinitely heavy nucleus of charge Z which is placed in the center of coordinates, r12 is distance between the electrons. E is energy of the two electrons. Conventionally, this is so called total energy which is equal to the sum of the sequential ionization energies (or potentials IP) of the first and second electrons, E = E1 + E2 = – (IP1 + IP2) < 0. Spin coordinates in wave function and corresponding interaction operators in Hamiltonian are excluded for the sake of simplicity. Here and further atomic units me = e = ћ = 1 are used. Since the Eq. (1) can not be solved analytically exactly[5–10] an approximate or numerically exact solution is sought as expansion in a series under necessary condition of the total energy minimization:
i are the position vectors of electrons, r1 and r2 stand for distances from the first and second electrons to the infinitely heavy nucleus of charge Z which is placed in the center of coordinates, r12 is distance between the electrons. E is energy of the two electrons. Conventionally, this is so called total energy which is equal to the sum of the sequential ionization energies (or potentials IP) of the first and second electrons, E = E1 + E2 = – (IP1 + IP2) < 0. Spin coordinates in wave function and corresponding interaction operators in Hamiltonian are excluded for the sake of simplicity. Here and further atomic units me = e = ћ = 1 are used. Since the Eq. (1) can not be solved analytically exactly[5–10] an approximate or numerically exact solution is sought as expansion in a series under necessary condition of the total energy minimization: | (2) |
3. The Contradiction between the Differential and Integral Forms of Eq. (1)
3.1. General
- Let us take the wave function in a very general form (in spherical coordinates) Ψ = Ψ(r1, θ1, φ1, r2, θ2, φ2) and assume it be an exact parameter-free or a very accurate variation solution of Eq. (2). Then we have:
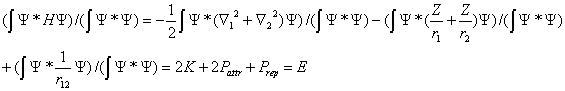 | , (3) |
3.2. Kellner Function
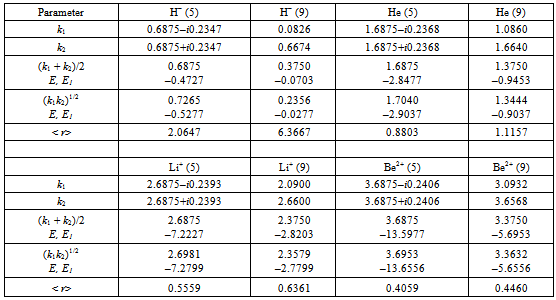
- In order to expose the insoluble contradiction most clearly let us choose the simplest Kellner’s orthonormal variational radial wave function[8]:
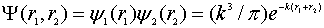 | (4) |
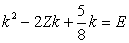 | (5) |
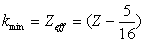 | (6) |
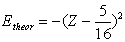 | (7) |
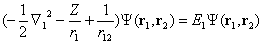 | (8) |
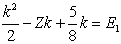 | (9) |
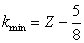 | (10) |
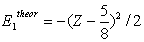 | (11) |
3.3. Eckart Function
- The described strong violation under integration of the initial true balance of attraction/repulsion operators leading to a too much high value of k is not specific feature of just the wave function (4). The same result is got if use Eckart-type function:
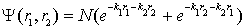 | (12) |
3.4. Mean Radial Distance in Highly Precise Hylleraas-type Calculations
- To treat the Hylleraas-type functions is excessive because those explicitly depend on inter-electronic distance r12 and evidently make sure that the electrons never occupy the same point in the space and tend to be far from one another. Therefore, this kind of function tends to make repulsion between the electrons weaker. Therefore, it tends to strengthen attraction. But the mistake found in the present study is just too much strong attraction owing to the physically senseless summing (doubling) of the attraction operators, after integration! Then irrespective to the number of variation parameters and variables, any wave function produced by Eq. (1) describes an artificial system intermediate between proper helium atom and He+ ion. It does not describe the helium atom.Nonetheless, there is an interesting property of Hylleraas-type functions that would be advantageous in calculations. Lowering energy by means of enlarging the mean <r12> distance by those functions is followed by corresponding increase of mean radial distance <r> and, consequently, of volume of the atom. For example, expectation values of radial distance in helium atom and negative hydrogen ion equal 0.929 and 2.710, respectively[1]. These values are larger than those calculated from Eq. (5): 0.880 and 2.065. That is, this kind of function increases the volume and lowers energy of the atom. However, these mean distances are substantially smaller than those calculated from Eq. (9): 1.1157 and 6.3667, respectively. The difference of the radii, in picometers, is enormous, especially in view of the X-ray diffraction measurement precision (0.1-0.01 pm): 9.88 and 193.50, respectively. It makes impossible to compare interatomic distances in molecules and condensed matter with atomic radii. In Section 4, we shall demonstrate one of examples of strong advantage of the present radii.
3.5. Inertial Nature of the Correlation Energy ΔE1
- The correlation energies, that is, calculation errors ΔE1 and ΔE are defined here as differences between the experimental or exact values of mean total or orbital energies and those theoretical:
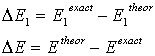 | (13) |
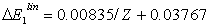 | (14) |
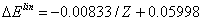 | (15) |
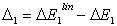 | (16) |
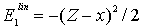 | (17) |
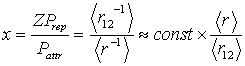 | (18) |
|
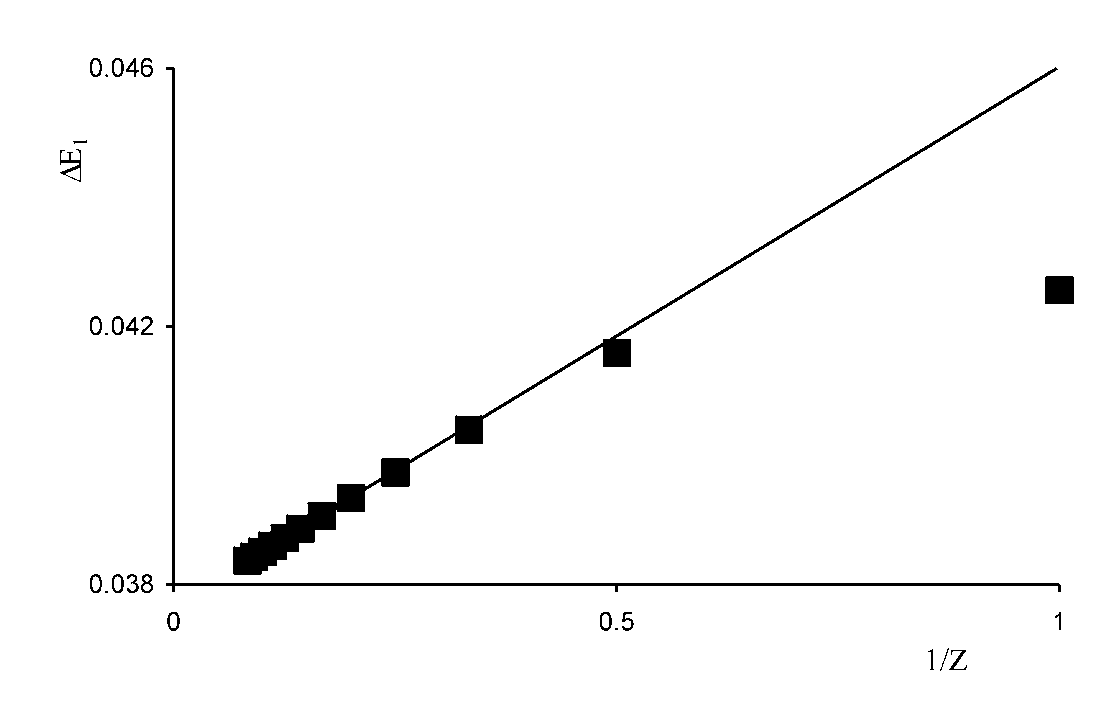 | Figure 1. Dependence of the correlation energy ΔE1 on the inverse nuclear charge, for the helium isoelectronic series. The linear trend refers to the correlation energy ΔE1lin accounting for the repulsion energy error, filled quadrangles – to ΔE1 |
4. Problem of Relation between Atomic Radii, Interatomic Distances and Bond Energies: Homonuclear Diatomic Molecules of the Elements from H through Ne
- The necessity of a time-resolved description of electrons’ movement in a two-electron atom strongly supports an assumption of the present author on necessity of a time-resolved consideration of covalent bonding in homonuclear molecules. The idea is that electrons tend to visit the area between nuclei namely the overlap area at different time intervals[22]. Then the covalent interaction can be represented by simple overlap of spherical atoms preserving radii of isolated atoms (RA), and dissociation energy D0 of a homonuclear molecule is proportional to the depth of overlapping of atoms dR (dR = 2 RA – R, R is the inter-nuclear distance). Both D0 and R are known from experimental table data. A beautiful curve of the dependence D0 (dR):
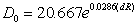 | (19) |
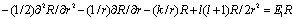 | (20) |
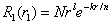 | (21) |
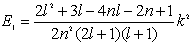 | (22) |
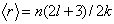 | (23) |
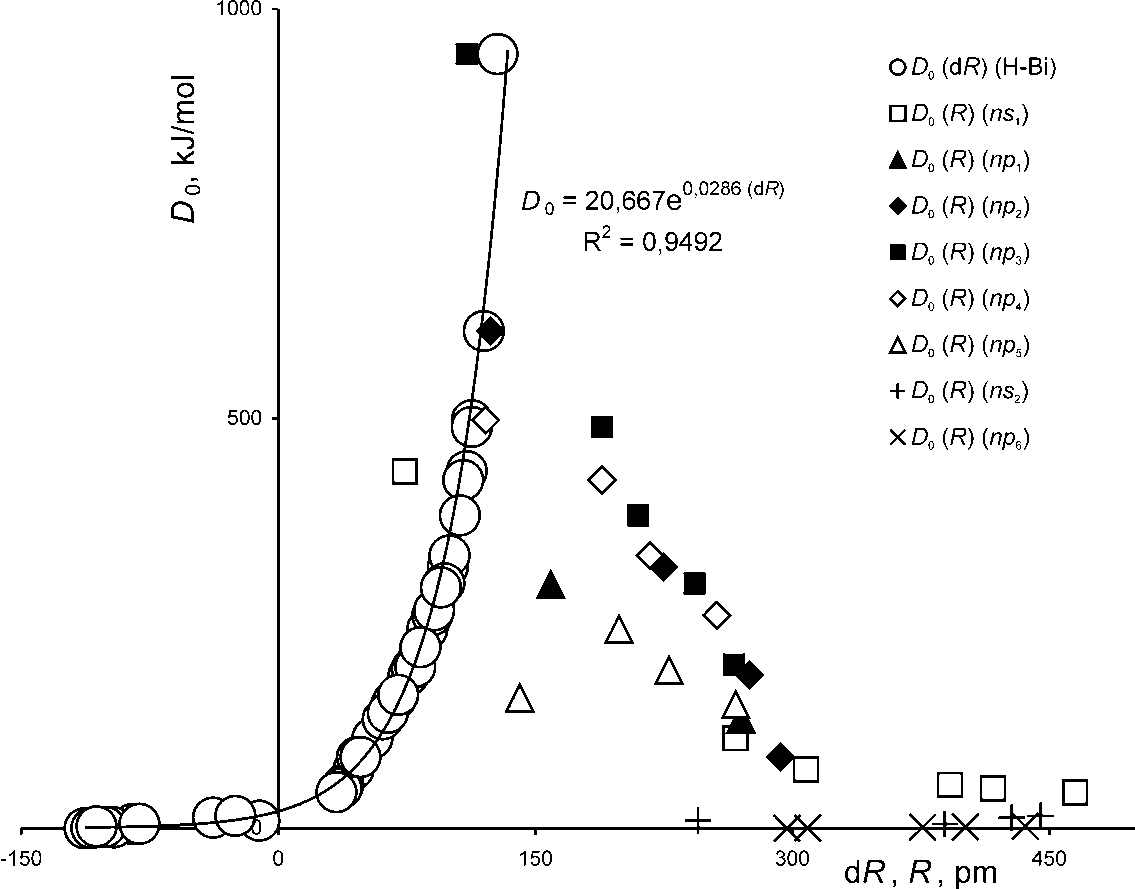 | Figure 2. Empirical dependences D0 (dR) and D0 (R) for covalent and van der Waals homonuclear diatomic molecules[22] |
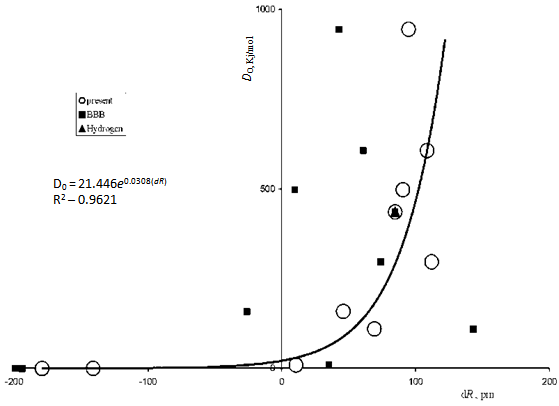 | Figure 3. Theoretical dependences D0 (dR) for diatomic molecules of the elements from hydrogen to neon[20]. Open circles refer to the author’s calculations, filled quadrangles (BBB) – to the data of Bunge et al.[23] |
- Due to this reduction of the difference, a dependence of dissociation energies of diatomic molecules on the degree of overlapping of atomic orbitals becomes apparent. On Fig. 3, two dependences D0 (dR) (dR = 2<r> – R) are presented, those with use of conventional and of new radii. One can easily see a considerable difference in the scatter of corresponding points. The “new” dependence is described by the curve:
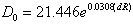 | (24) |
5. Conclusions
- On the basis of above considerations we come to conclusion that there certainly exists an insoluble contradiction in the conventional theory of the ground state of helium atom and helium-like ions. The contradiction is that between the rules of summing of energy operators and energy values of different particles. The theory allows precise calculating the value of total energy. But each of the electrons in a helium atom does not possess a half of the total energy. Their energies are equal to ionization energy. The remaining energy is that of relaxation to the helium ion state which is characterized by much deeper energy minimum and lesser volume. More important is the wave function of the system. It should accurately correspond to true physical laws of motion of the electrons. The conventional theory ignores some of them. The central deficiency of the theory is a substantial overestimation of attraction of electrons to nucleus caused by incorrect summing the attraction operators. It is correct to sum energies of the electrons. Those are just numbers. But it is incorrect to sum the attraction energy operators related to different electrons. The Eq. (1) requires wave function satisfy to the proportion ‘one attraction versus one repulsion’ whereas the integrated one with any trial wave function requires it satisfy the proportion ‘two attractions versus one repulsion’. Owing to the incorrectness any solution of the Eq. (1) has an exceeding curvature. Moreover, it does not describe real motion of the electrons in a two-electron atom. In fact, calculating total energy is a cunning trick aiming to get solution of the two-electron atom problem through the only one stationary Schrödinger equation and entirely in terms of probability density, like the hydrogen atom problem. Unfortunately, the two-electron problem cannot be solved in such a way. It requires a time-resolved treating because electrons can visit the same point in space at different instants of time. Therefore, trajectories of the electrons should be explored. This is not surprising for the particles possessing the rest mass. Hence, it is necessary to use Newton or Feynman mechanics. In both cases the problem of correlation, in its present form, disappears because the electrons turn out to visit the same point at different instants of time. Then the function (4) becomes very suitable stationary function describing an averaged in time distribution of electron density and all interactions.The reported contradiction is met not only in the theory of two-electron atoms. It is principal one also in theory of many electron atoms and molecules. Therefore, to get a correct benchmark solution of the two-electron problem is very important.In conclusion, we find reasonable to distinguish three entities that govern the ground state of a two-electron atom: 1) volume independent probability represented in the stationary Schrödinger equation by the wave function (4); 2) volume dependent probability to find electrons close to one another; it is supposed to be steered by 3) classical dynamics of electron wave packets caused by their inertial properties.
References
| [1] | Drake, G, Springer Handbook of Atomic, Molecular, and Optical Physics. Chapter 11. Springer, New York (2006) |
| [2] | Sims, J. S., George W. L., Satterfield S. G. and others, Accelerating Scientific Discovery Through Computation and Visualization J. Res. Natl. Inst. Stand. Technol. 107, 223–245 (2002) |
| [3] | Schwartz, C, Experiment and Theory in Computations of the He Atom Ground State Int. J. Mod. Phys. E 15 877 (2006) |
| [4] | Nakashima, H, Nakatsuji, H, Solving the Schrödinger equation for helium atom and its isoelectronic ions with the free iterative complement interaction (ICI) method. J. Chem. Phys. 127, 224104- (1)–224104- (14) (2007) |
| [5] | Fock, V, Näherungsmethode zur Lösung des quantenmechanischen Mehrkörperproblems. Z. f. Phys. 61, 126–148 (1930) |
| [6] | Bethe, H, Salpeter, E, Quantum Mechanics of One- and Two-Electron Atoms; Springer-Verlag, Berlin (1957) |
| [7] | Landau, L, Lifshitz, E, Quantum Mechanics. Non-relativistic Theory; Butterworth-Heinemann, London (1995) |
| [8] | Kellner, G, Die Ionisierungsspannung des Heliums nach der Schrödingerschen Theorie. Z. f. Phys. 44, 91–109 (1927) |
| [9] | Hylleraas, E, Neue Berechnung der Energie des Heliums im Grundzustande, sowie des tiefsten Terms von Ortho-Helium. Z. Phys. 54, 347–366 (1929) |
| [10] | Pekeris, L, Ground state of two-electron atoms. Phys. Rev. 112, 1649–1658 (1958) |
| [11] | Thakkar, A, Smith, V, Compact and accurate integral - transform wave functions. I. The 1 1S state of the helium-like ions from H– through Mg10+. Phys. Rev. A. 15, 1–15 (1977) |
| [12] | Koga, T, Aoki, S, Charge and radial correlations in helium and helium-like atoms. Theor. Chim. Acta. 78, 165–173 (1990) |
| [13] | Frolov, A, Two-stage strategy for high-precision variational calculations. Phys. Rev. A. 57, 2436–2439 (1998) |
| [14] | Korobov, V, Yelkhovsky, A, Ionization potential of the helium atom. Phys. Rev. Lett. 87, 193003- (1)–193003- (4) (2001) |
| [15] | Taylor, G, Parr, R, Superposition of configurations: the helium atom. Proc. Natl. Acad. Sci. USA. 38, 154–160 (1952) |
| [16] | Sims, J, Hagstrom, S, High-precision Hy–CI variational calculations for the ground state of neutral helium and helium-like ions. Intl. J. Quant. Chem. 90, 1600–1609 (2002) |
| [17] | Hylleras, E, On the Ground State Term of the Two-Electron Problem of H−, He, Li+, Be++, etc. Z. f. Phys. 65, 209–219 (1930) |
| [18] | Ivanova, E, Safronova, U, Perturbation theory in calculations of atomic energy levels. J. Phys. B. 8, 1591–1602 (1975) |
| [19] | Zamastil, J, Сızek, J, Skala, L, Simanek, M, Convergence study of the 1/Z expansion for the energy levels of two - electron atoms. Phys. Rev. A. 81, 032118- (1)–032118- (6) (2010) |
| [20] | Ignatiev, V, How to solve the problem of dynamical correlation of electrons in the ground-state helium atom? Intl. J. Quant. Chem. 111, 2568–2574 (2011) |
| [21] | Shevkunov, S, Feynman path integral computer simulation of helium atom electron shell. Matem. Mod. 22, 79–96 (2010) |
| [22] | Ignatiev, V.D, Interpermeable atoms in homonuclear diatomic molecules. J. Mol. Struct.: THEOCHEM. 819, 102 – 108 (2007) |
| [23] | Bunge, F., Barrientos, J. A. and Bunge A. V. Roothaan – Hartree–Fock wave functions. At. Data Nucl. Data Tables. 53, 113–162 (1993). |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML