-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2013; 3(1): 10-25
doi:10.5923/j.ijtmp.20130301.03
Lossless Transmission Lines Terminated by in-Series Connected RL-Loads Parallel to C-Load
Vasil G. Angelov
Department of Mathematics, University of Mining and Geology “St. I. Rilski”, Sofia, 1700, Bulgaria
Correspondence to: Vasil G. Angelov , Department of Mathematics, University of Mining and Geology “St. I. Rilski”, Sofia, 1700, Bulgaria.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The paper deals with an analysis of transmission line terminated by in series connected RL-loads parallel to C-load. The mixed problem for Telegrapher equations to a periodic problem on the boundary is reduced. The obtained neutral system of equations in an operator form is presented. The fixed points of the operator in question are solutions of the periodic problem.
Keywords: Lossless Transmission Lines, RLC-Loads, Periodic Solutions, Fixed Point Theorems
Cite this paper: Vasil G. Angelov , Lossless Transmission Lines Terminated by in-Series Connected RL-Loads Parallel to C-Load, International Journal of Theoretical and Mathematical Physics, Vol. 3 No. 1, 2013, pp. 10-25. doi: 10.5923/j.ijtmp.20130301.03.
Article Outline
1. Introduction
- The main purpose of the present paper is to consider a lossless transmission line loaded by in series connected nonlinear RL-loads parallel to C-load. Such a configuration arises not only in radio frequencies devices but in various geophysical studies as well (cf.[1]). Our goal is to demonstrate the advantages of our method[2] used in analogous problems. So we came up with an approach to solve this set of problems (cf.[3]-[7]).The primary purpose of the present paper is twofold. First, to formulate the mixed problem for hyperbolic Telegrapher equations corresponding to the nonlinear circuits on Figure 1. The boundary conditions are nonlinear ones in view of the nonlinear characteristics of the loads. Important first step on the base of Kirchoff’s law is to derive the boundary conditions in the form of differential equations on the boundary. This is done in 2.1. Reducing the mixed problem to a neutral system on the boundary is made in 2.2 following the technique from[2],[5] and[6]. Second, to present a method for solving neutral equations with “bad” (non-Lipschitz) nonlinearities. In 2.3 the domains of the nonlinear characteristics are defined. They have to possess strictly positive lower bounds and namely Assumption (C) for capacitive functions and (L) for inductive functions ensure that. In 2.3 the choice of functional spaces and a family of pseudo-metrics is directly related to the operator representation of the periodic problem in 2.4. Let us point out that the extension of Bielecki norm allows to overcome the difficulties caused by nonlinearity of the characteristic functions. The key role plays Lemma 3. It guaranties that the fixed points of the operator defined in 2.4 are periodic solutions of the neutral system and conversely. The main result is Theorem 1 (cf. 2.5) and its proof consists of two parts. The first one is to show that operator B maps the set
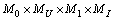 into itself. The second one is to show that B is contractive operator. The fixed point of B is the required periodic solution. The numerical example in 2.6 shows that for applications are required only inequalities obtained in the proof of the main theorem.
into itself. The second one is to show that B is contractive operator. The fixed point of B is the required periodic solution. The numerical example in 2.6 shows that for applications are required only inequalities obtained in the proof of the main theorem. 2. Main Results
2.1. Formulation of the Problem
- Let
 be the length of the transmission line and
be the length of the transmission line and 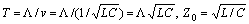 , where L is per unit length inductance and C – per unit-length capacitance. In accordance of Kirchoff’s voltage-law (Figure 1) we have to add the voltages of the elements
, where L is per unit length inductance and C – per unit-length capacitance. In accordance of Kirchoff’s voltage-law (Figure 1) we have to add the voltages of the elements 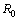 and
and 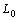 after that to define the current of
after that to define the current of 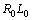 and finally to add it with the current of
and finally to add it with the current of 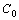 . In the real cases parallel to
. In the real cases parallel to 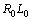 and
and 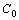 is connected an input voltage
is connected an input voltage 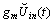 , where
, where 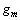 is the amplification coefficient. Since we have to add the currents one can replaced
is the amplification coefficient. Since we have to add the currents one can replaced 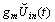 by an equivalent current source
by an equivalent current source 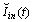 . We assume that the second end is terminated by the same configuration.Assume that
. We assume that the second end is terminated by the same configuration.Assume that 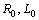 and
and 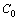 are nonlinear elements, that is,
are nonlinear elements, that is, 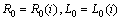 and
and 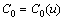 are nonlinear functions. So we have
are nonlinear functions. So we have 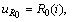
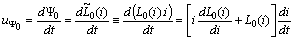 and then
and then 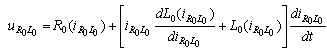
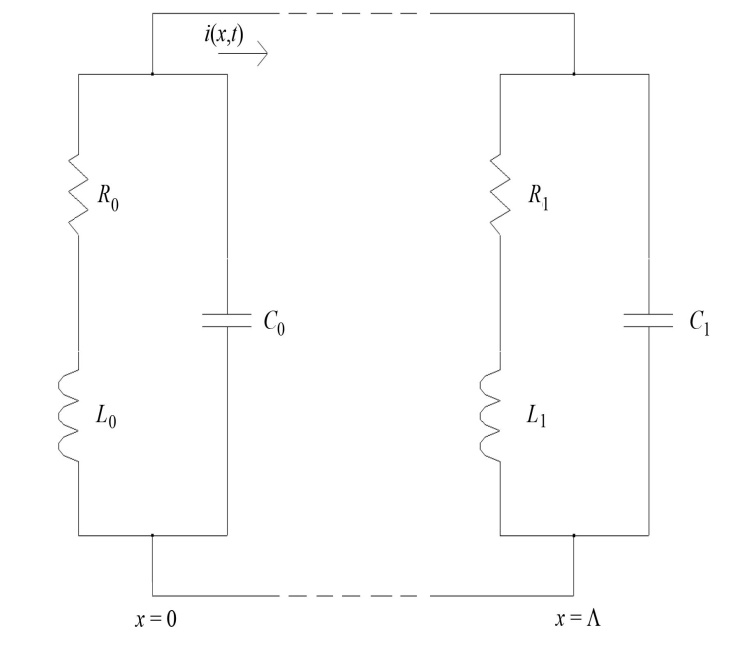 | Figure 1. Lossless transmission line terminated at both ends by in series connected RL-loads parallel to C-load |
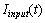 is connected parallel to RL-elements then Kirchoff’s current-law yields
is connected parallel to RL-elements then Kirchoff’s current-law yields 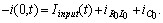 | (1) |
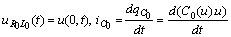 then
then 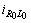 can be found as a solution of differential equation
can be found as a solution of differential equation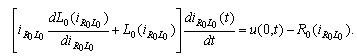 But
But 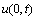 is unknown too and then from (1) we have
is unknown too and then from (1) we have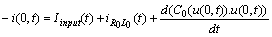 or one more differential equation:
or one more differential equation: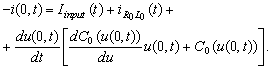 Analogously for the right end we have
Analogously for the right end we have 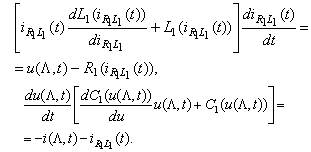 Now we are able to formulate the initial-boundary value (mixed) problem for the transmission line equations: to find a solution
Now we are able to formulate the initial-boundary value (mixed) problem for the transmission line equations: to find a solution  of the first order partial differential system of hyperbolic type
of the first order partial differential system of hyperbolic type 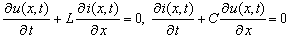 | (2) |
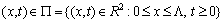 satisfying the initial conditions
satisfying the initial conditions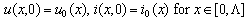 | (3) |
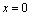
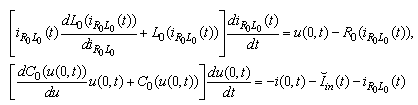 | (4) |
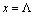
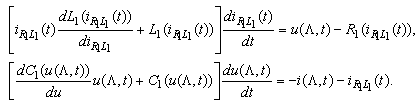 | (5) |
2.2. Reducing the Mixed Problem to an Initial Value Problem on the Boundary
- We proceed from the lossless transmission line equations
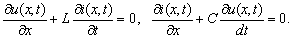 | (6) |
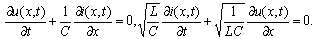 | (7) |
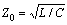 we get:
we get: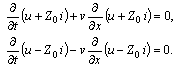 | (8) |
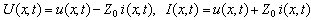 and hence
and hence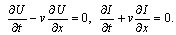 It follows
It follows 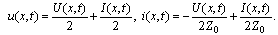 | (9) |
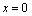 and
and 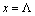 we have
we have 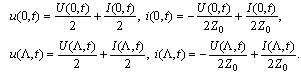 Replace them in (4) and (5) we obtain
Replace them in (4) and (5) we obtain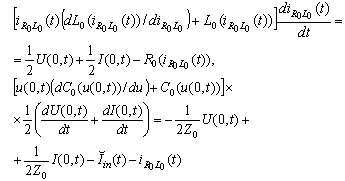 and
and 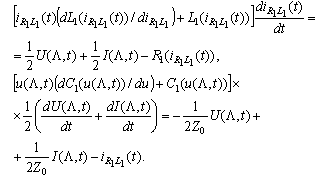 But
But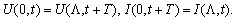 We assume that the unknown functions are
We assume that the unknown functions are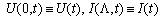 and then in view of
and then in view of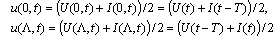 solve with respect to the derivatives we reach the system
solve with respect to the derivatives we reach the system 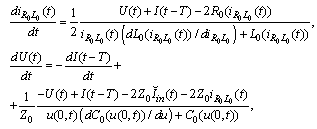 | (10) |
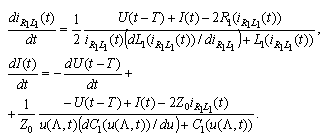 So we have obtained a neutral system of differential equations with retarded arguments.
So we have obtained a neutral system of differential equations with retarded arguments.2.3. Estimates of the Arising Nonlinearities and Introducing Metrics
- We consider C-V characteristics
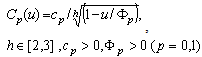 , for
, for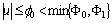 where
where 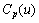 have a strictly positive lower bounds. Put
have a strictly positive lower bounds. Put 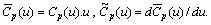 ..Then
..Then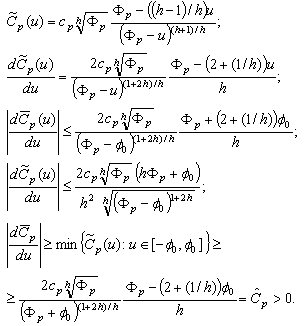 For the I-V characteristics we assume
For the I-V characteristics we assume 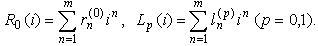 Then
Then 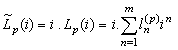 . For
. For 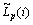 we get
we get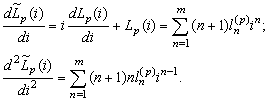 Assumptions (L):
Assumptions (L): 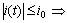
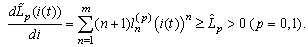 Assumptions (C):
Assumptions (C): 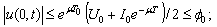
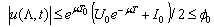 For the V-I characteristics we assume that they are of polynomial type:
For the V-I characteristics we assume that they are of polynomial type: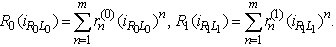 We introduce the sets for the unknown functions
We introduce the sets for the unknown functions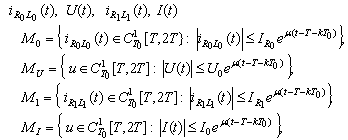
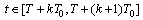
 where
where 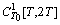 is the set of all continuously differentiable
is the set of all continuously differentiable 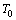 -periodic functions and
-periodic functions and 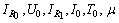 are positive constants (chosen below) and
are positive constants (chosen below) and 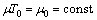 Introduce the metrics
Introduce the metrics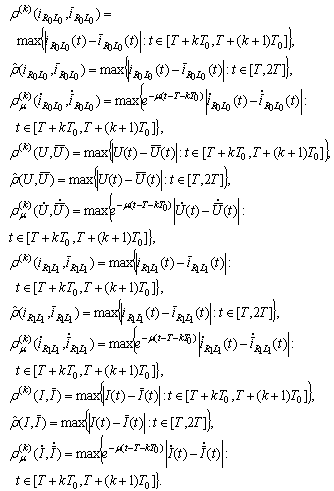 The set
The set 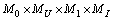 turns out into a complete metric space with respect to the metric:
turns out into a complete metric space with respect to the metric: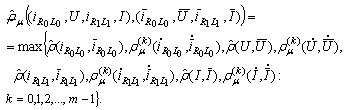
2.4. Operator Presentation of the Periodic Problem
- Now we formulate the main problem: to find a
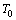 -periodic solution
-periodic solution 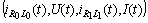 of the system (10) on the interval
of the system (10) on the interval 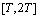 coinciding with prescribed
coinciding with prescribed 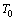 -periodic initial functions
-periodic initial functions 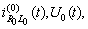
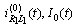 on the interval respectively:
on the interval respectively: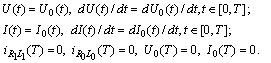 Remark 1. As in[3] one can shift the initial function of the mixed problem from the interval
Remark 1. As in[3] one can shift the initial function of the mixed problem from the interval 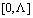 along the characteristic to the interval
along the characteristic to the interval 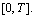 The main difficulty is to define a suitable operator whose fixed points are solutions sought. We define it in the following way: the four-tuple functions
The main difficulty is to define a suitable operator whose fixed points are solutions sought. We define it in the following way: the four-tuple functions 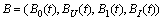 are defined on every interval
are defined on every interval 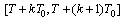 (for every k = 0,1,2, …, m-1) by the expressions
(for every k = 0,1,2, …, m-1) by the expressions 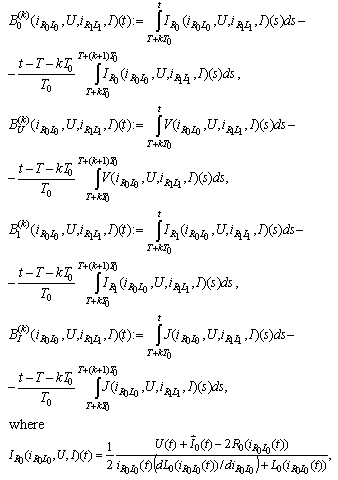
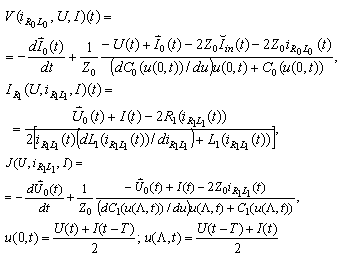 and
and 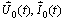 are translated to the right initial functions
are translated to the right initial functions 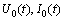 over
over  .From now on the following assumptions will be fulfilled:(E):
.From now on the following assumptions will be fulfilled:(E): 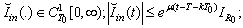 (IN):
(IN): 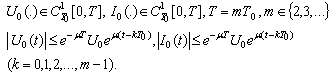 It follows
It follows 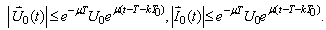 Lemma 1. If (E) and (IN) are satisfied and
Lemma 1. If (E) and (IN) are satisfied and 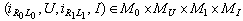 then
then 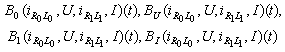 are
are 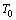 -periodic ones.Lemma 2. If
-periodic ones.Lemma 2. If 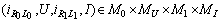 then
then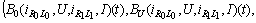
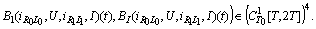 The proofs can be accomplished as in[5],[6].The following lemma guaranties that the fixed points of the above defined operator are periodic solutions of the neutral system (10).Lemma 3. The periodic problem (10) has a solution
The proofs can be accomplished as in[5],[6].The following lemma guaranties that the fixed points of the above defined operator are periodic solutions of the neutral system (10).Lemma 3. The periodic problem (10) has a solution 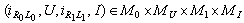
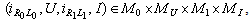 that is,
that is,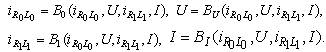 Proof: Let
Proof: Let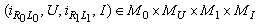 be a
be a 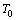 -periodic solution of (10). Then after integration of the first equation we have (recall that
-periodic solution of (10). Then after integration of the first equation we have (recall that 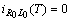 ):
): 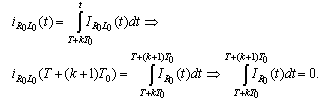 Therefore
Therefore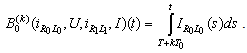 Analogously we obtain
Analogously we obtain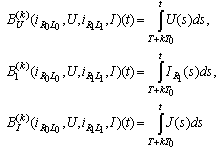 that is,
that is, 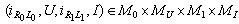 is a fixed point of B.Conversely, let
is a fixed point of B.Conversely, let 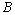 have a fixed point
have a fixed point 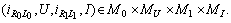 Then
Then
 If we assume
If we assume 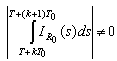 in view of
in view of 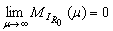 one obtains a contradiction. It follows
one obtains a contradiction. It follows 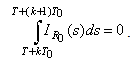 Analogously
Analogously 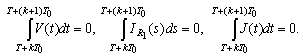 Consequently
Consequently 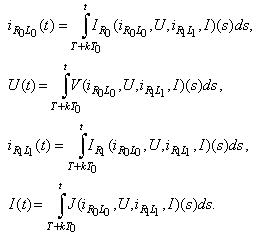 Differentiating the last equalities we conclude that (10) has
Differentiating the last equalities we conclude that (10) has 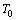 -periodic solution.Lemma 3 is thus proved.
-periodic solution.Lemma 3 is thus proved. 2.5. Existence-Uniqueness of Periodic Solution
- The main result contains in the followingTheorem 1. Let assumptions (L), (C), (E) and (IN) be fulfilled. Then there exists a unique T0-periodic solution of (10).Proof: We show that
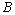 maps
maps 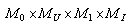 into itself. Indeed
into itself. Indeed 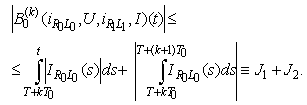 We have
We have Further on we have
Further on we have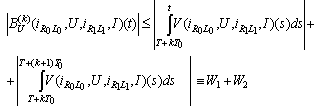 and
and and
and On the other hand
On the other hand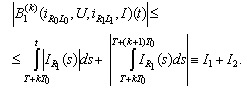 We have
We have Then
Then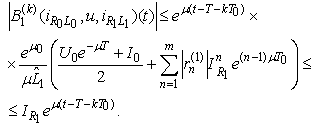 Finally
Finally 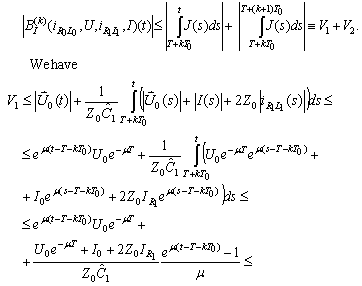
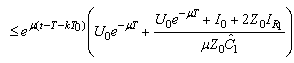 and
and It remains to obtain the Lipschitz estimates for the right-hand sides of the equations. Omitting calculation of the partial derivatives we obtain:
It remains to obtain the Lipschitz estimates for the right-hand sides of the equations. Omitting calculation of the partial derivatives we obtain: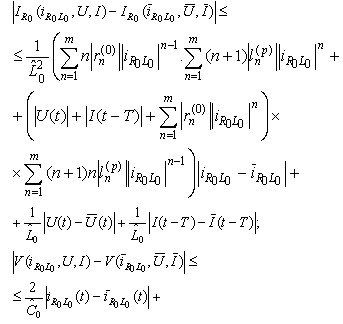
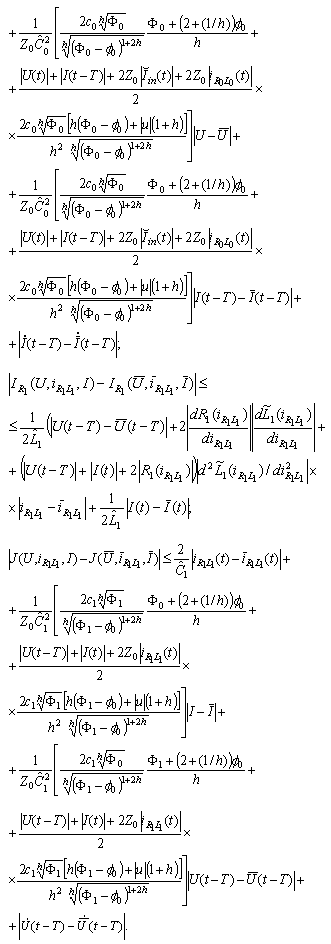 Then
Then
 It follows
It follows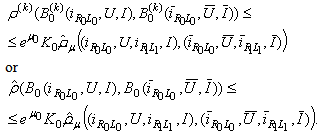 Further on we get
Further on we get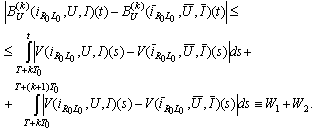

 It follows
It follows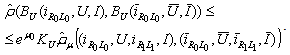 For the third component we obtain:
For the third component we obtain: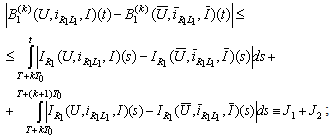

 For the fourth component we have
For the fourth component we have
 It follows
It follows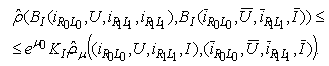 For the derivatives we obtain
For the derivatives we obtain
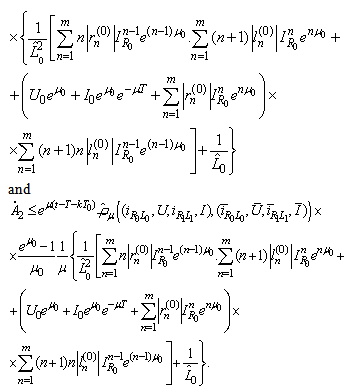 Consequently
Consequently Further on we have
Further on we have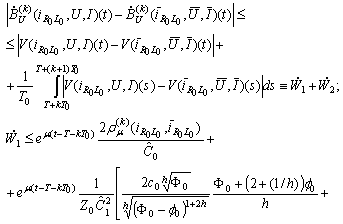
 ThereforeConsequently
ThereforeConsequently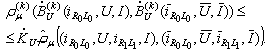 Further on we have
Further on we have 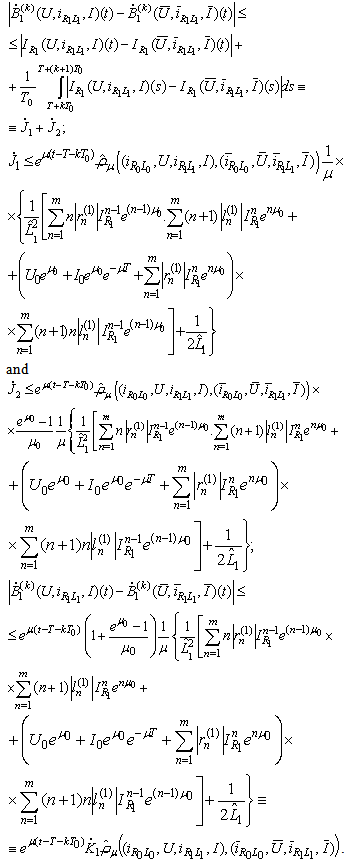 Then
Then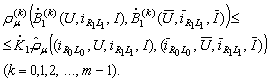 For the last component of the derivative we obtain
For the last component of the derivative we obtain and
and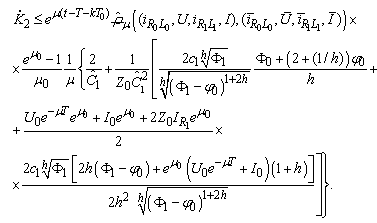 On the other hand
On the other hand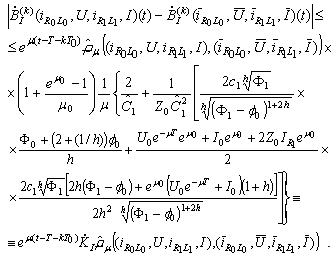 Consequently
Consequently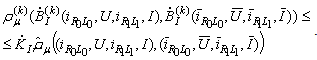 .Finally we have
.Finally we have 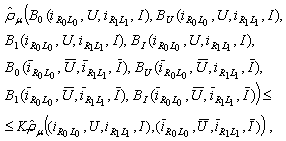 where
where 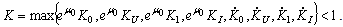 Then B has a unique fixed point which is a periodic solution of (10).Theorem 1 is thus proved.
Then B has a unique fixed point which is a periodic solution of (10).Theorem 1 is thus proved. 2.6. Numerical Example
- For a transmission line with length
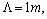
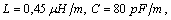
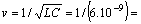
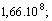
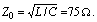 Then
Then 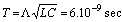 .Let us check the propagation of waves with
.Let us check the propagation of waves with 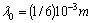 . We have
. We have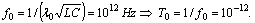 We choose
We choose  , then
, then 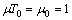 and
and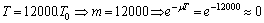 .We choose resistive elements with the following V-I characteristics
.We choose resistive elements with the following V-I characteristics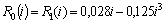 and inductive elements with
and inductive elements with 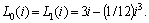 Then
Then 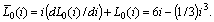 For
For  one obtains
one obtains 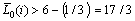
 .Let us take
.Let us take 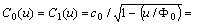
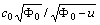 where
where 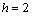 . Let us choose
. Let us choose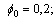
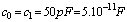 and
and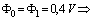
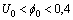 . Then
. Then 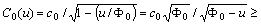
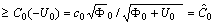
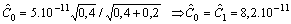 .Then the above inequalities for
.Then the above inequalities for 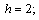
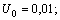
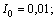
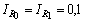 become:
become: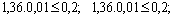
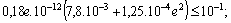
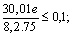
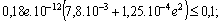
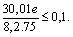 We calculate just
We calculate just 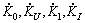 since
since 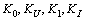 are of order
are of order 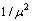 :
: 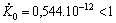 ;
; 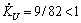 ;
; 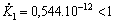 ;
; 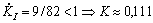 .
.3. Conclusions
- We consider transmission lines neglecting the lossies. This makes it possible to find conditions for the existence and uniqueness of periodic regimes. This natural physical fact is confirmed by the mathematical method we apply. • In order to prove an existence-uniqueness theorem we introduce an operator (unknown in the literature up to now) whose fixed points are periodic solutions of the problem stated. We apply contractive fixed point theorems in metric spaces. By extended Bielecki metrics we overcome the difficulties caused by polynomial and transcendental nonlinearities.• The numerical example demonstrates a frame of applicability of the theory exposed (for instance to design of circuits) and shows that the method could be applied checking few simple inequalities between the basic specific parameter of the lines and loads.• We show a unified approach for solving problems for analysis of transmission lines terminated various configurations of nonlinear loads. In contrast to various results devoted to numerical methods[8]-[14] we obtain an explicit approximated solution. • We emphasize on the fact that first we prove not only an existence but and uniqueness of the solution as well. So our successive approximations tend to this solution. All other methods need such a uniqueness result. Unfortunately in most papers the uniqueness is not ensured.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML