A. A. Kleshchev , E. I. Kuznetsova
Saint – Petersburg State Navy Technical University, Russia, 190008, Saint , Petersburg, Lotsmanskaya st., 3
Correspondence to: A. A. Kleshchev , Saint – Petersburg State Navy Technical University, Russia, 190008, Saint , Petersburg, Lotsmanskaya st., 3.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The done before analysis of the low frequency resonances of the elastic spheroidal bodies, irradiating and establishing by the harmonic signal[1], supplemented with the research of the elastic spheroidal shell, irradiating and establishing by the pulse signal.
Keywords:
Diffraction, Lame Constants, Potential, Elastic Shell, Boundary Conditions
Cite this paper: A. A. Kleshchev , E. I. Kuznetsova , About Low Frequency Resonances of Elastic Spheroidal Shells, Irradiating and Establishing by Harmonic and Pulse Signals, International Journal of Theoretical and Mathematical Physics, Vol. 3 No. 1, 2013, pp. 4-9. doi: 10.5923/j.ijtmp.20130301.02.
1. Introduction
In the paper is showing, what the low frequency reso-nances of the elastic prolate spheroidal shells are disco-vered by the axissymmetrical irradiation.
2.The First Part of the Article Investigat the Results of the Numerical Experiment for the Determination of the Low Frequency Resonances of the Elastic Spheroidal Shell, Irradiating and Establishing by the Harmonic Signal
The frequencies of the first resonances of the elastic oscillations of spheroidal bodies may be established very exactly with the help of their sections of a radiation and scattering (of the integral characteristics)[2, 3]. These results may be obtained and by analysis of the angular characteristics of the radiation 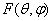 and the scattering
and the scattering 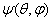 of the sound for these bodies. Let us consider a scatterer in the form of an isotropic spheroidal shell, illuminating along axis of the rotation of the shell (the axis – symmetrical problem). All the potentials, including the plane wave potential
of the sound for these bodies. Let us consider a scatterer in the form of an isotropic spheroidal shell, illuminating along axis of the rotation of the shell (the axis – symmetrical problem). All the potentials, including the plane wave potential 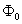 , the scattered wave potential
, the scattered wave potential 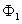 , the scalar shell potential
, the scalar shell potential 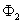 , the component
, the component 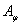 of the vector
of the vector 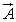 potential and the potential
potential and the potential 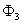 of the gas filling the shell, can be expanded in spheroidal wave functions[2, 3]:
of the gas filling the shell, can be expanded in spheroidal wave functions[2, 3]: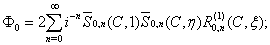 | (1) |
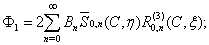 | (2) |
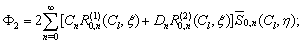 | (3) |
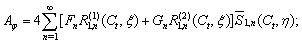 | (4) |
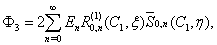 | (5) |
where 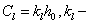 the wavenumber of the longitudinal elastic wave,
the wavenumber of the longitudinal elastic wave, 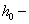 semi – focus distance;
semi – focus distance; 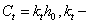 the wavenumber of the transverse elastic wave;
the wavenumber of the transverse elastic wave; 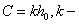 the wavenumber of the sound wave in the fluid;
the wavenumber of the sound wave in the fluid; 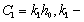 the wavenumber of the sound wave in the gas filling the shell;
the wavenumber of the sound wave in the gas filling the shell; 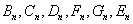 are unknown expansion coefficients. The expansion coefficients are de4termined from the physical boundary conditions preset at the two surfaces of the shell
are unknown expansion coefficients. The expansion coefficients are de4termined from the physical boundary conditions preset at the two surfaces of the shell 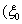 and
and 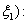 1. the continuity of the normal displacement component at both of the boundaries,
1. the continuity of the normal displacement component at both of the boundaries, 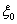 and
and 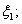 2. the identity between the normal stress in the elastic shell and the sound pressure in the liguid
2. the identity between the normal stress in the elastic shell and the sound pressure in the liguid 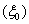 or in the gas
or in the gas 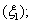 3. the absence of tangential stress at both of the shell boundaries,
3. the absence of tangential stress at both of the shell boundaries, 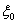 and
and 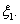 The corresponding expressions for the boundary conditions have in the form[2]:
The corresponding expressions for the boundary conditions have in the form[2]: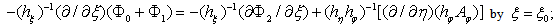 | (6) |
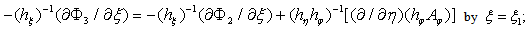 | (7) |
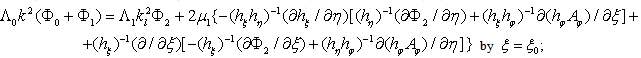 | (8) |
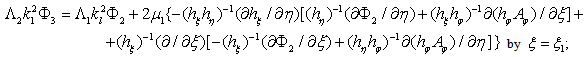 | (9) |
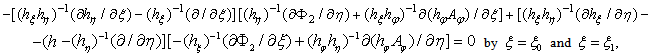 | (10) |
where 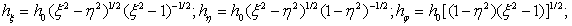 the liquid,
the liquid, 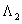 is the bulk compression coefficient of the gas filling the shell.The substitution of series (1) – (5) in boundary conditions (6) – (10) yields an infinite system of equations for determining the desired coefficients. The infinite system is solved by the truncation method. The number of retained terms of expansions (1) – (5) is the greater, the greater the wave size for the given potential.On the figure 1 are presented the meetings of the modulus
is the bulk compression coefficient of the gas filling the shell.The substitution of series (1) – (5) in boundary conditions (6) – (10) yields an infinite system of equations for determining the desired coefficients. The infinite system is solved by the truncation method. The number of retained terms of expansions (1) – (5) is the greater, the greater the wave size for the given potential.On the figure 1 are presented the meetings of the modulus 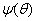 of the steel gas – filled prolate spheroidal shell with the external coordinate
of the steel gas – filled prolate spheroidal shell with the external coordinate 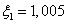 and the internal coordinate
and the internal coordinate 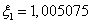 by the wave dimensions
by the wave dimensions 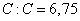 (the curve 1),
(the curve 1), 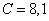 (the curve 2), (curve 3).
(the curve 2), (curve 3). 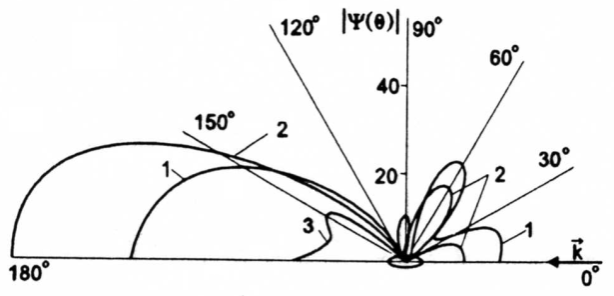 | Figure 1. The moduluses of the angular characteristics of the scattering 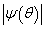 of the elastic (steel) gas-filled spheroidal shell of the elastic (steel) gas-filled spheroidal shell |
The scattering of the such form is irradiated by the plane harmonic sound wave of single amplitude. From the figure 1 we see, what the maximum area engages the modulus of the angular characteristics 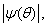 corresponding to the wave dimension
corresponding to the wave dimension 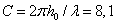
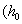 is the semi – focal distance of the prolate spheroidal coordinate system,
is the semi – focal distance of the prolate spheroidal coordinate system, 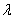 is the length of the sound wave in liquid). The meaning
is the length of the sound wave in liquid). The meaning 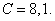 is very near to the value
is very near to the value 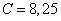 , corresponding to the resonance of the zero symmetrical Lamb wave[2, 3]. As well we see, the shade lobe of the scattering determined by the angles
, corresponding to the resonance of the zero symmetrical Lamb wave[2, 3]. As well we see, the shade lobe of the scattering determined by the angles 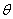 near to
near to 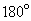 grows not monotonously as it is observed by the ideal scatterings, but one may be changed in the any way. For example, by
grows not monotonously as it is observed by the ideal scatterings, but one may be changed in the any way. For example, by 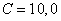 (Figure 1) the shade lobe at the value less, than by
(Figure 1) the shade lobe at the value less, than by 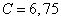 and
and 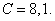 The moduluses of the angular characteristics of the sound radiation
The moduluses of the angular characteristics of the sound radiation 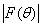 this shell, exciting by the harmonic source, are presented on figure 2 for the wave dimensions
this shell, exciting by the harmonic source, are presented on figure 2 for the wave dimensions 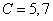 (curve 1),
(curve 1), 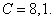 (the curve 2),
(the curve 2), 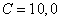 (the curve 3).
(the curve 3). 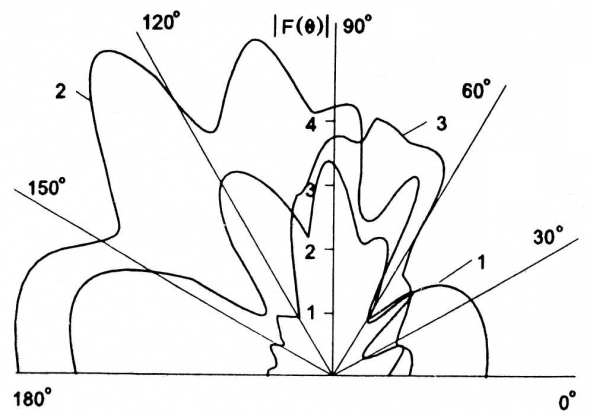 | Figure 2. The moduluses of the angular characteristics of the radiation  by the elastic (steel) gas-filled spheroidal shell by the elastic (steel) gas-filled spheroidal shell |
And here the picture is repeated: the area under the curve 2  is found maximum. So we cocslude, that the low frequency resonances of the elastic oscillations may be determined with the help of integral and angular characteristics of the radiation and scattering of the sound by these bodies.
is found maximum. So we cocslude, that the low frequency resonances of the elastic oscillations may be determined with the help of integral and angular characteristics of the radiation and scattering of the sound by these bodies.
3.The Second of the Article Investigates the Results of Numerical Experiment for Determination of the Low Frequency Resonances of the Elastic Prolate Spheroidal Shell, Irradiating and Establishing by the Pulse Signal
The fallen pulse  with the basis frequency
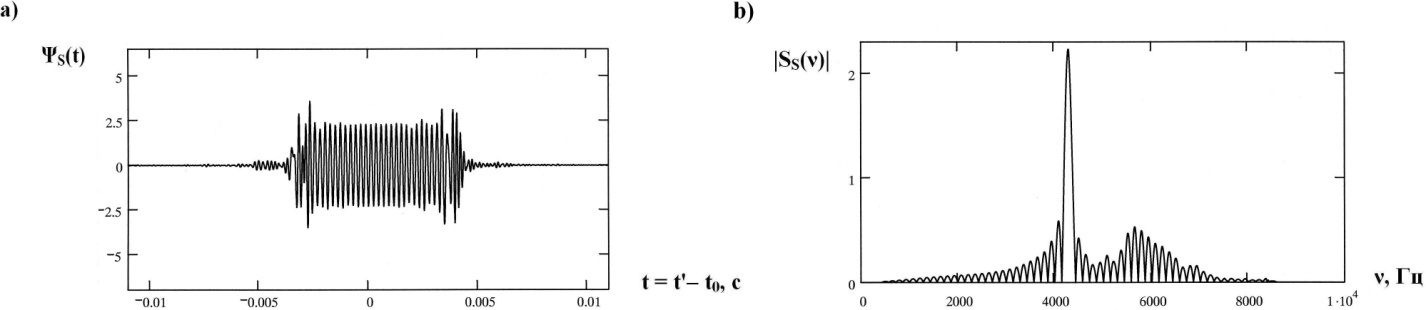
with the basis frequency 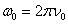 (Figure 3, a) has the following spectrum
(Figure 3, a) has the following spectrum 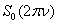 (Figure 3, b)[4]:
(Figure 3, b)[4]: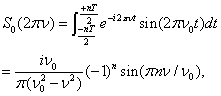 | (11) |
where: 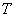 – the period of the harmonic signal with the frequency
– the period of the harmonic signal with the frequency 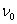 ,
, 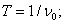
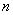 – number of the periods in pulse;
– number of the periods in pulse; 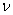 – the current circular frequency.The spectrum
– the current circular frequency.The spectrum 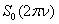 connects with by the return Fourier transform[4]:
connects with by the return Fourier transform[4]: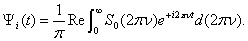 | (12) |
With the help 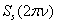 and
and 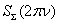 found the pulses
found the pulses 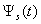 and
and 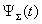 (scattered and diffracted according)[4 – 15]:
(scattered and diffracted according)[4 – 15]: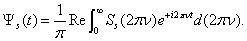 | (13) |
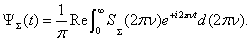 | (14) |
For the computation of the spectrums 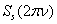 and
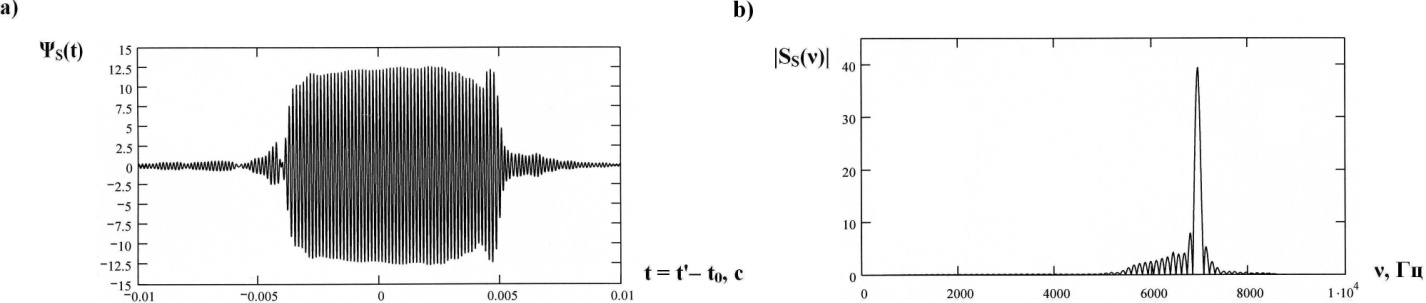
and 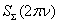 are used the amplitude – phase characteristics of the sound scattering at spheroidal shell by the stationary (harmonic) irradiation[2].At the Figure 4, 5 and 6 were representing the pulses of the back scattering
are used the amplitude – phase characteristics of the sound scattering at spheroidal shell by the stationary (harmonic) irradiation[2].At the Figure 4, 5 and 6 were representing the pulses of the back scattering 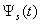 (a) and the normalized moduluses of the spectrums
(a) and the normalized moduluses of the spectrums 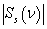 of the pulses
of the pulses 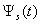 on the resonances (Figure 5 and 6) and outside of the resonance (Figure 4).
on the resonances (Figure 5 and 6) and outside of the resonance (Figure 4). 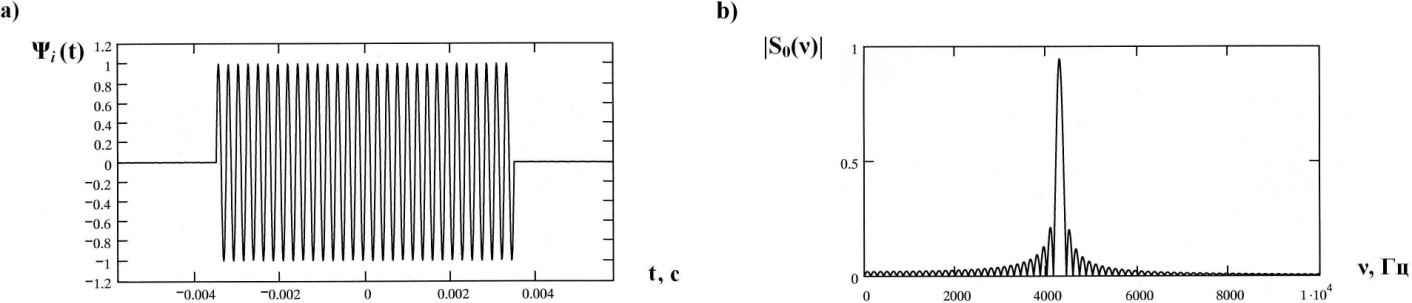 | Figure 3. The fallen pulse  (a); the modulus of the spectrum (a); the modulus of the spectrum  of the pulse of the pulse 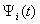 (b) (b) |
 | Figure 4. The pulse of the back scattering 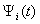 (a); the normalized modulus of the spectrum (a); the normalized modulus of the spectrum 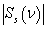 of the pulse of the pulse 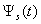 (b); (b);  |
 | Figure 5. The pulse of the back scattering  (a); the normalized modulus of the spectrum (a); the normalized modulus of the spectrum 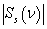 of the pulse of the pulse 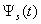 (b); (b);  |
 | Figure 6. The pulse of the back scattering 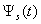 (a); the normalized modulus of the spectrum (a); the normalized modulus of the spectrum 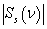 of the pulse of the pulse  (b); (b);  |
At Figure 7, 8 and 9 were representing the scattered pulses 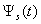 in the direction
in the direction  and them the normalized moduluses on the resonances (Figure 8 and 9) and outside resonance (Figure 7).
and them the normalized moduluses on the resonances (Figure 8 and 9) and outside resonance (Figure 7).  | Figure 7. The scattered pulse  in the direction in the direction 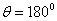 (a); the normalized modulus of the spectrum (a); the normalized modulus of the spectrum 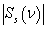 of the pulse of the pulse 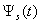 (b); (b); 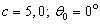 |
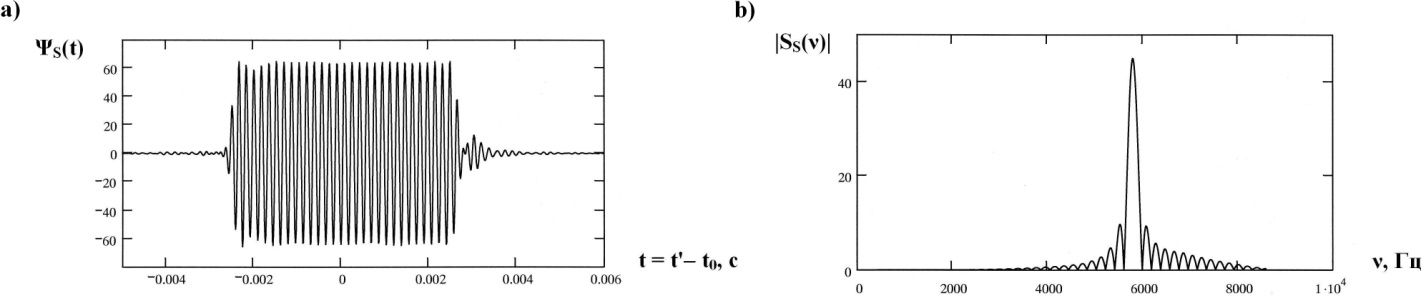 | Figure 8. The scattered pulse 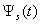 in the direction in the direction 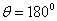 (a); the normalized modulus of the spectrum (a); the normalized modulus of the spectrum 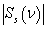 of the pulse of the pulse 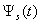 (b); (b); 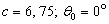 |
 | Figure 9. The scattered pulse  in the direction in the direction 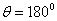 (a); the normalized modulus of the spectrum (a); the normalized modulus of the spectrum 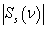 of the pulse of the pulse 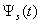 (b); (b); 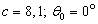 |
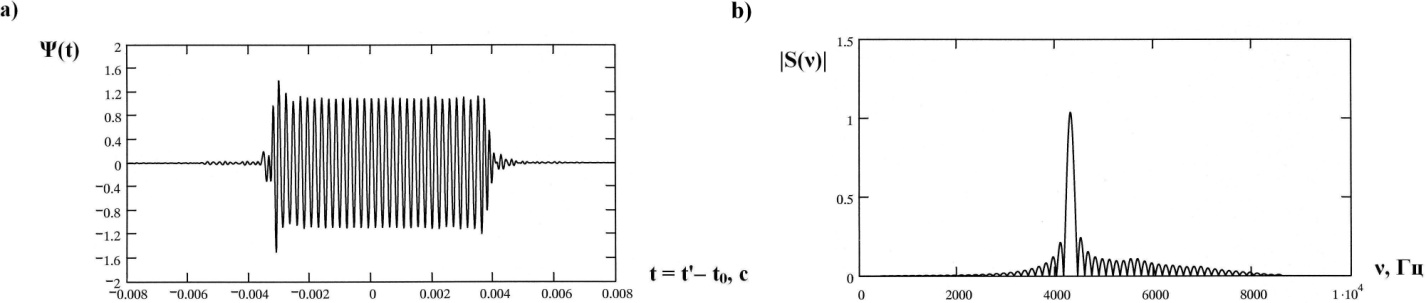 | Figure 10. The radiated pulse  in the direction in the direction  (a); the normalized modulus of the spectrum (a); the normalized modulus of the spectrum  of the pulse of the pulse 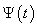 (b); (b); 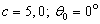 |
 | Figure 11. The radiated pulse  in the direction in the direction 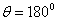 (a); the normalized modulus of the spectrum (a); the normalized modulus of the spectrum 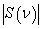 of the radiated pulse of the radiated pulse 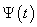 (b); (b); 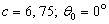 |
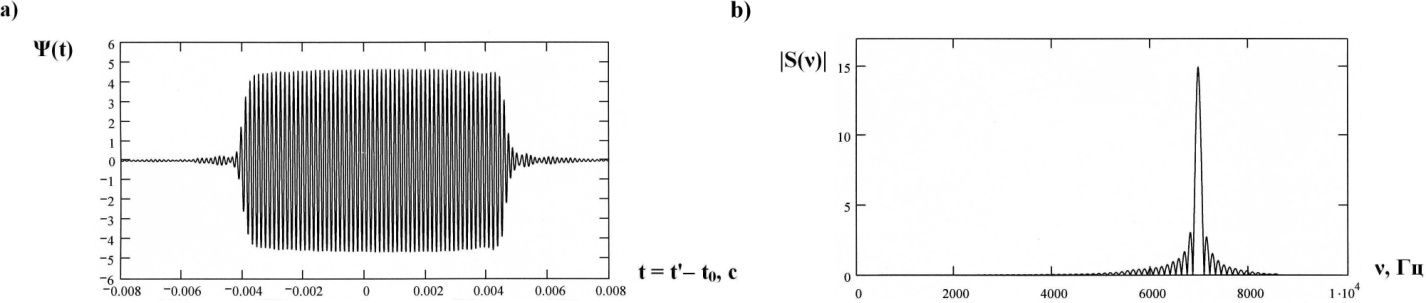 | Figure 12. The radiated pulse 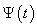 in the direction in the direction 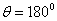 (a); the normalized modulus of the spectrum (a); the normalized modulus of the spectrum 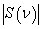 of the radiated pulse of the radiated pulse 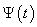 (b); (b); 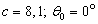 |
At Figure 10, 11 and 12 were representing the radiated pulses 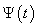 in the direction
in the direction 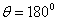 and them the normalized moduluses on the resonances (Figure 11 and 12) and outside resonance 9 Figure 10).From the comparison of these figures we see, what the amplitudes of the pulses on the resonances much higher.
and them the normalized moduluses on the resonances (Figure 11 and 12) and outside resonance 9 Figure 10).From the comparison of these figures we see, what the amplitudes of the pulses on the resonances much higher.
4. Сonclusions
With help of the numerical experiment are found the low frequency resonances of the elastic spheroidal shell by the axis – symmetrical illumination.
ACKNOWLEDGMENTS
This work was supported as part of research under State Contract no P242 of April 21. 2010, within the Federal Target Program “Human Capital in Sciense and Education for Education for Innovative Russia, 2009 – 2013”.
References
| [1] | A.A. Kleshchev. J. Techn. Acoust. 2, 27 (1995). |
| [2] | A.A. Kleshchev. Hydroacoustic Scatterers (Prima, St. Petersburg, 2012)[in Russia]. |
| [3] | A.A. Kleshchev. Phys. Acoust. 38, 361 (1992). |
| [4] | A.A. Kharcevich. Spectrum and Analysis. (GITTL, Moskau, 1957)[in Russia]. |
| [5] | Gaunaurd G. C., Werby M. F. J. A. S. A. 77, 2081 (1985). |
| [6] | Werby M. F., Gaunard G. C. J. A. S. A. 82, 1369 (1987). |
| [7] | Werby M. F., Green L. H. J. A. S. A. 74, 625 (1983). |
| [8] | Werby M. F., Green L. H. J. A. S. A. 76, 1227 (1984). |
| [9] | Werby M. F., Green L. H. J. A. S. A. 81, (1987). |
| [10] | Werby M. F., Tango G. J. J. A. S. A. 79, 1260 (1986). |
| [11] | A. A. Kleshchev. Sov. Phys. Acoust. 57, 381 (2011). |
| [12] | A. A. Kleshchev, E. I. Kuznetsova. Phys. Acoust. 57,495 (2011). |
| [13] | A. A. Kleshchev. Diffraction and Propagation of Waves in Elastic Mediums and Bodies. (Vlas, St.- Petersburg, 2002)[in Russian]. |
| [14] | A. A. Kleshchev. Difraction, Radiation and Propagation of Elastic Waves. (Profprint, St.- Petersburg, 2006)[in Russian]. |
| [15] | A. A. Kleshchev. Phys. Acoust. 58, 338 (2012). |

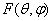 and the scattering
and the scattering 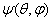 of the sound for these bodies. Let us consider a scatterer in the form of an isotropic spheroidal shell, illuminating along axis of the rotation of the shell (the axis – symmetrical problem). All the potentials, including the plane wave potential
of the sound for these bodies. Let us consider a scatterer in the form of an isotropic spheroidal shell, illuminating along axis of the rotation of the shell (the axis – symmetrical problem). All the potentials, including the plane wave potential 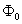 , the scattered wave potential
, the scattered wave potential 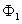 , the scalar shell potential
, the scalar shell potential 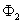 , the component
, the component 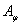 of the vector
of the vector 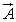 potential and the potential
potential and the potential 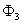 of the gas filling the shell, can be expanded in spheroidal wave functions[2, 3]:
of the gas filling the shell, can be expanded in spheroidal wave functions[2, 3]: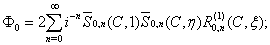
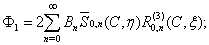
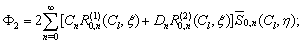
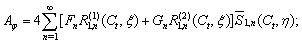
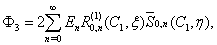
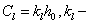 the wavenumber of the longitudinal elastic wave,
the wavenumber of the longitudinal elastic wave, 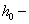 semi – focus distance;
semi – focus distance; 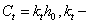 the wavenumber of the transverse elastic wave;
the wavenumber of the transverse elastic wave; 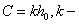 the wavenumber of the sound wave in the fluid;
the wavenumber of the sound wave in the fluid; 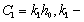 the wavenumber of the sound wave in the gas filling the shell;
the wavenumber of the sound wave in the gas filling the shell;  are unknown expansion coefficients. The expansion coefficients are de4termined from the physical boundary conditions preset at the two surfaces of the shell
are unknown expansion coefficients. The expansion coefficients are de4termined from the physical boundary conditions preset at the two surfaces of the shell  and
and 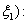 1. the continuity of the normal displacement component at both of the boundaries,
1. the continuity of the normal displacement component at both of the boundaries, 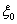 and
and 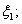 2. the identity between the normal stress in the elastic shell and the sound pressure in the liguid
2. the identity between the normal stress in the elastic shell and the sound pressure in the liguid 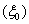 or in the gas
or in the gas 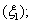 3. the absence of tangential stress at both of the shell boundaries,
3. the absence of tangential stress at both of the shell boundaries, 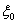 and
and 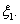 The corresponding expressions for the boundary conditions have in the form[2]:
The corresponding expressions for the boundary conditions have in the form[2]: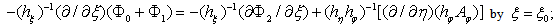
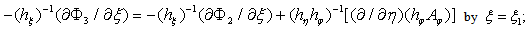
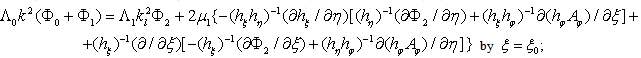
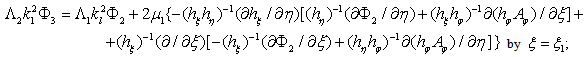
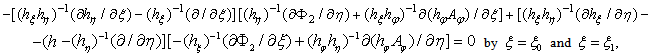
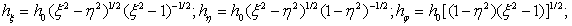 the liquid,
the liquid,  is the bulk compression coefficient of the gas filling the shell.The substitution of series (1) – (5) in boundary conditions (6) – (10) yields an infinite system of equations for determining the desired coefficients. The infinite system is solved by the truncation method. The number of retained terms of expansions (1) – (5) is the greater, the greater the wave size for the given potential.On the figure 1 are presented the meetings of the modulus
is the bulk compression coefficient of the gas filling the shell.The substitution of series (1) – (5) in boundary conditions (6) – (10) yields an infinite system of equations for determining the desired coefficients. The infinite system is solved by the truncation method. The number of retained terms of expansions (1) – (5) is the greater, the greater the wave size for the given potential.On the figure 1 are presented the meetings of the modulus  of the steel gas – filled prolate spheroidal shell with the external coordinate
of the steel gas – filled prolate spheroidal shell with the external coordinate  and the internal coordinate
and the internal coordinate 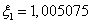 by the wave dimensions
by the wave dimensions 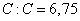 (the curve 1),
(the curve 1), 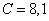 (the curve 2), (curve 3).
(the curve 2), (curve 3). 
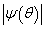 of the elastic (steel) gas-filled spheroidal shell
of the elastic (steel) gas-filled spheroidal shell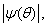 corresponding to the wave dimension
corresponding to the wave dimension 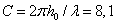
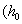 is the semi – focal distance of the prolate spheroidal coordinate system,
is the semi – focal distance of the prolate spheroidal coordinate system, 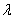 is the length of the sound wave in liquid). The meaning
is the length of the sound wave in liquid). The meaning 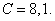 is very near to the value
is very near to the value 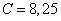 , corresponding to the resonance of the zero symmetrical Lamb wave[2, 3]. As well we see, the shade lobe of the scattering determined by the angles
, corresponding to the resonance of the zero symmetrical Lamb wave[2, 3]. As well we see, the shade lobe of the scattering determined by the angles  near to
near to  grows not monotonously as it is observed by the ideal scatterings, but one may be changed in the any way. For example, by
grows not monotonously as it is observed by the ideal scatterings, but one may be changed in the any way. For example, by 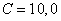 (Figure 1) the shade lobe at the value less, than by
(Figure 1) the shade lobe at the value less, than by 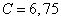 and
and 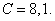 The moduluses of the angular characteristics of the sound radiation
The moduluses of the angular characteristics of the sound radiation 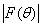 this shell, exciting by the harmonic source, are presented on figure 2 for the wave dimensions
this shell, exciting by the harmonic source, are presented on figure 2 for the wave dimensions 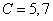 (curve 1),
(curve 1), 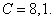 (the curve 2),
(the curve 2), 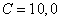 (the curve 3).
(the curve 3). 
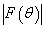 by the elastic (steel) gas-filled spheroidal shell
by the elastic (steel) gas-filled spheroidal shell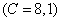 is found maximum. So we cocslude, that the low frequency resonances of the elastic oscillations may be determined with the help of integral and angular characteristics of the radiation and scattering of the sound by these bodies.
is found maximum. So we cocslude, that the low frequency resonances of the elastic oscillations may be determined with the help of integral and angular characteristics of the radiation and scattering of the sound by these bodies.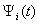 with the basis frequency
with the basis frequency 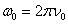 (Figure 3, a) has the following spectrum
(Figure 3, a) has the following spectrum 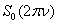 (Figure 3, b)[4]:
(Figure 3, b)[4]: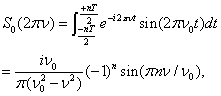
 – the period of the harmonic signal with the frequency
– the period of the harmonic signal with the frequency  ,
, 
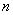 – number of the periods in pulse;
– number of the periods in pulse; 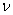 – the current circular frequency.The spectrum
– the current circular frequency.The spectrum 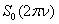 connects with by the return Fourier transform[4]:
connects with by the return Fourier transform[4]: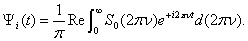
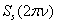 and
and 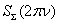 found the pulses
found the pulses 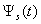 and
and 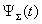 (scattered and diffracted according)[4 – 15]:
(scattered and diffracted according)[4 – 15]: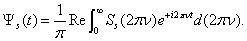
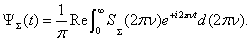
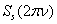 and
and 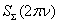 are used the amplitude – phase characteristics of the sound scattering at spheroidal shell by the stationary (harmonic) irradiation[2].At the Figure 4, 5 and 6 were representing the pulses of the back scattering
are used the amplitude – phase characteristics of the sound scattering at spheroidal shell by the stationary (harmonic) irradiation[2].At the Figure 4, 5 and 6 were representing the pulses of the back scattering 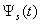 (a) and the normalized moduluses of the spectrums
(a) and the normalized moduluses of the spectrums 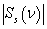 of the pulses
of the pulses 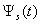 on the resonances (Figure 5 and 6) and outside of the resonance (Figure 4).
on the resonances (Figure 5 and 6) and outside of the resonance (Figure 4). 
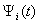 (a); the modulus of the spectrum
(a); the modulus of the spectrum 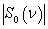 of the pulse
of the pulse 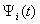 (b)
(b)
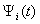 (a); the normalized modulus of the spectrum
(a); the normalized modulus of the spectrum 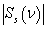 of the pulse
of the pulse 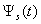 (b);
(b); 

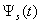 (a); the normalized modulus of the spectrum
(a); the normalized modulus of the spectrum  of the pulse
of the pulse 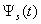 (b);
(b); 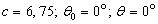

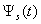 (a); the normalized modulus of the spectrum
(a); the normalized modulus of the spectrum 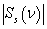 of the pulse
of the pulse 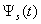 (b);
(b); 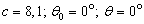
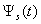 in the direction
in the direction 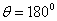 and them the normalized moduluses on the resonances (Figure 8 and 9) and outside resonance (Figure 7).
and them the normalized moduluses on the resonances (Figure 8 and 9) and outside resonance (Figure 7). 
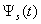 in the direction
in the direction 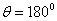 (a); the normalized modulus of the spectrum
(a); the normalized modulus of the spectrum 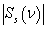 of the pulse
of the pulse 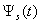 (b);
(b); 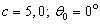

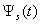 in the direction
in the direction 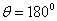 (a); the normalized modulus of the spectrum
(a); the normalized modulus of the spectrum 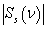 of the pulse
of the pulse 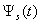 (b);
(b); 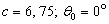

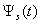 in the direction
in the direction 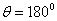 (a); the normalized modulus of the spectrum
(a); the normalized modulus of the spectrum 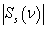 of the pulse
of the pulse 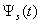 (b);
(b); 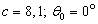

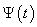 in the direction
in the direction 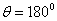 (a); the normalized modulus of the spectrum
(a); the normalized modulus of the spectrum 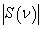 of the pulse
of the pulse 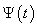 (b);
(b); 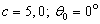

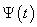 in the direction
in the direction  (a); the normalized modulus of the spectrum
(a); the normalized modulus of the spectrum 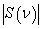 of the radiated pulse
of the radiated pulse 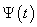 (b);
(b); 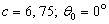

 in the direction
in the direction  (a); the normalized modulus of the spectrum
(a); the normalized modulus of the spectrum  of the radiated pulse
of the radiated pulse 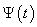 (b);
(b); 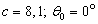
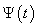 in the direction
in the direction 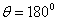 and them the normalized moduluses on the resonances (Figure 11 and 12) and outside resonance 9 Figure 10).From the comparison of these figures we see, what the amplitudes of the pulses on the resonances much higher.
and them the normalized moduluses on the resonances (Figure 11 and 12) and outside resonance 9 Figure 10).From the comparison of these figures we see, what the amplitudes of the pulses on the resonances much higher.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML