1. Introduction

Major equations of the theory of elasticity indicate links between deformation and tension (the generalized law by Hooky). Besides, the major equations, in general, contain the components of movement and tension as well. Although, we may manage the system of equations to contain only the components of tension or the components ofmovement. [3][4]

The major equations of the theory of flat elasticity are associated with the following border-line tasks:

a) Find elastic balance of the body when active outer areas are known.

b) Find elastic balance of the body if the point movements in the surface of the body are known.

Those essential practical difficulties connected with solving the main theory of flat elasticity, impulse discovering the efficient ways. This way was investigated by G. Kolosov and then this investigation was extended by N. Muskhelishvili. It indicates the use of the theory of complex variable functions. Tensions and movements may be expressed with aid of theory of complex variable functions, as a results of it, the purpose is to find these functions in certain conditions and they are to meet particular requirements at boundary areas.

In the paper is discussed the problem of the first major limiting problem of elasticity theory[1]. Said problem is reduced to two Dirichlet boundary value problems and is given its effective solution.

2. Objectives

My goal was to solve the first main boundary task of flat elasticity according to those efficient ways mentioned in[2] monograph for the second main boundary task.

3. Methods

Effective ways of boundary value problem of theory of flat elasticity are given in Fundamental monograph of Georgian academician N. Muskhelishvili, circular areas and spheres that are conformally transformed on the circle by rational functions are also discussed in his monograph. Professor E. Obolashvili suggested[2] renovated way of solving the abovementioned tasks, this variant may lead to Dirichlet two tasks for circle.

We will givehere a main way of solving of first major task of the border of external environment of the ellipses outer area (sphere) will show it with some modifications. First, well map (transform) under discussion S area, on 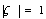on infinite flatness, circular hole reflection may be given with the following formula

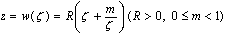(1)

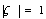Circumference corresponds to the ellipse with thecentre in coordinate origin and with half axis,.

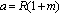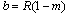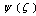The problem is to find holomorphic and functions in outer areas of the circle, which satisfy the condition on the boundary area

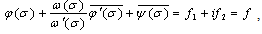(2)

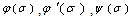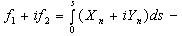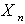Whererefers to any point on the circumference and under are meant functions boundary meaning, when. andand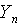 are the tension meanings (figures)

In our case well have

.

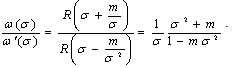So, (2) will be as followed

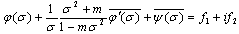(3)

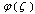Agree at the outset that outer forces combined vector or the contours 0, tension in infinite is 0 and there is no turning in the infinite. In this situation have that and 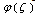will be holomorphic functions together with the infinite point in the outer area of the circle. Let's consider,that.

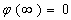By separating real and imaginative unreal parts from (3), we will get

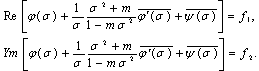(4)

From (4) it’s easy to get the following lets discuss function

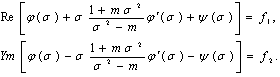Let’s discuss functions

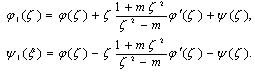(5)

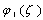It’s clear thatand are holomorphic functions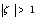circle. So we have

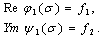(6)

(6)Represents Dirichlet two problems, which is enough to define and 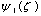functions.

We may rewrite it this way

We have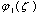andfunctions inarea. If we transform

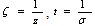Will have

,

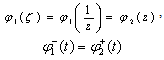We have

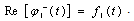From the last one well get

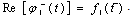If we consider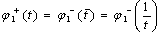finally, we will get

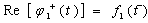It we consider Schwarz's well known formula for Dirichlet problem.[5],[6]. We will have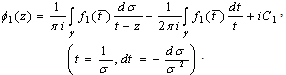

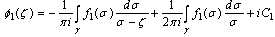(7)

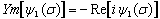If we take into consideration,we will have

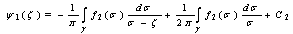(8)

From (5), (7) and (8) equalities well have

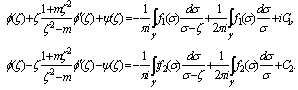(9)

From (9) we have

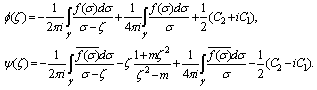(10)

If we take into consideration what I demand fromandfunctions from (10) we get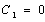 and.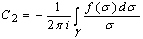

Finally

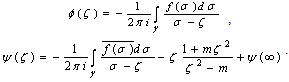So, and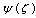are found.

4. Results

With the help of the given function meanings can be easily defined by the importance of tension.

For instance,

Where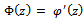and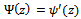

5. Conclusions

In conclusion, I must say that there are a lot of efficient ways to solve the major boundary tasks of the theory of flat elasticity.[7],[8],[9],[10].

In my opinion, the way defined in[2] is efficient, I must modestly speak about my minor works, expressed in modification and expansion of above mentioned way for first boundary problem for outer area of ellipse.

In addition to that, I was also studying various possible ways of major boundary tasks of the ellipse (internal environment).