S. L. Ilmenkov, A. A. Kleshchev
Saint-Petersburg State Navy Technical University, Saint-Petersburg, Lotsmanskaya str., 3, 190008, Russia
Correspondence to: S. L. Ilmenkov, Saint-Petersburg State Navy Technical University, Saint-Petersburg, Lotsmanskaya str., 3, 190008, Russia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Based on use of Debye’s potentials one can find the direct solution of the problem of definition of the characteristic equations for wave numbers of three-dimensional and axis-symmetrical (flexural and longitudinal) elastic waves in steel and aluminium cylindrical shells of various thickness.
Keywords:
Phase Velocity, Debye’s Potential, Flexural Wave, Longitudinal Wave, Three-Dimensional Problem, Axis-Symmetrical Problem
Cite this paper: S. L. Ilmenkov, A. A. Kleshchev, Phase Velocities of Three-Dimensional and Axis-Symmetrical Elastic Waves in Isotropic Cylindrical Shell, International Journal of Theoretical and Mathematical Physics, Vol. 2 No. 6, 2012, pp. 196-202. doi: 10.5923/j.ijtmp.20120206.04.
1. Introduction
The Debye’s potentials are used for the first time for a study of the three-dimensional flexural waves. The paper shows the existing of the three-dimensional and axis-symmetrical flexural waves in cylindrical shell (contrary to the cylindrical bar). The paper demonstrates the calculated values of the phase velocities of axis-symmetrical and three-dimensional flexural waves, while the phase velocities of the non-zero forms of three–symmetrical flexural waves are calculated for the first time. | Figure 1. The deformation of cylindrical shell for flexural (a) and longitudinal (b) axis- symmetrical waves |
2. The Three-Dimensional Flexural Waves in Cylindrical Shell
The first part of the article substantiates the effectiveness of usage of Debye’s potentials[1 – 3] for studying of three-dimensional flexural waves in cylindrical shell.In contrast to the bar the flexural wave in cylindrical shell can be three-dimensional and two-dimensional (axis-symmetrical). The deformation of cylindrical shell in the propagation of axis-symmetrical flexural (а) and longitudinal (b) waves in it is schematically shown in fig. 1. Let’s start with examination of three-dimensional flexural wave in isotropic cylindrical shell. In this case the same mathematical apparatus is used as in the study of flexural waves in bar[4], but the number of unknown quantities and the number of boundary conditions increase with the account of the second (internal) boundary surface. Now the expansions of the potentials Ф, V, U[5 – 15] take the form: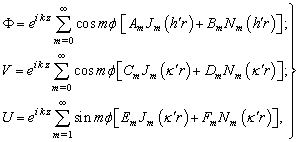 | (1) |
where 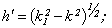
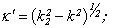
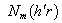 - are the Naman’s cylindrical function; Am , Bm , Cm , Dm , Em , Fm - are the unknown coefficients of expanding, which are calculated basing on the following physical boundary conditions on the external
- are the Naman’s cylindrical function; Am , Bm , Cm , Dm , Em , Fm - are the unknown coefficients of expanding, which are calculated basing on the following physical boundary conditions on the external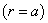 and inside
and inside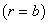 surfaces of the shell: there are no normal and tangent tensions on the both boundaries of the shell.We desire the analytical form of boundary conditions as following:
surfaces of the shell: there are no normal and tangent tensions on the both boundaries of the shell.We desire the analytical form of boundary conditions as following: | (2) |
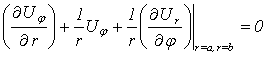 | (3) |
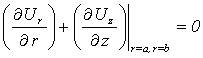 | (4) |
If we substitute (1) in the boundary conditions (2) - (4), we’ll get the determinant of six order[5 – 15]: | (5) |
where 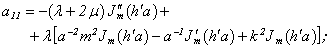
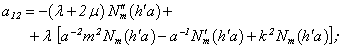
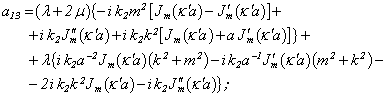
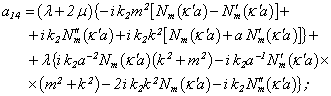
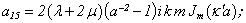
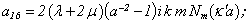
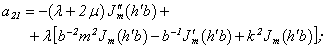
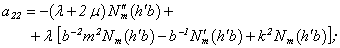
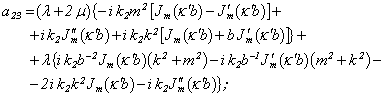
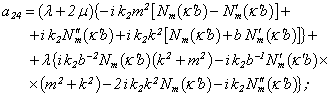
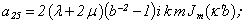
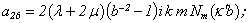
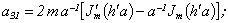
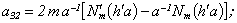
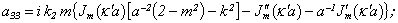
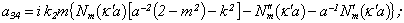
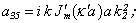
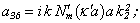
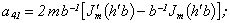
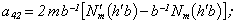
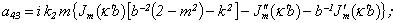
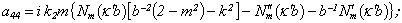
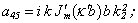
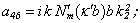
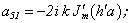
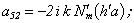
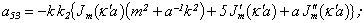
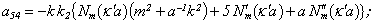
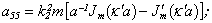
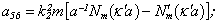
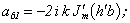
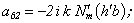
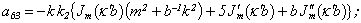
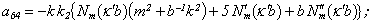
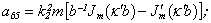
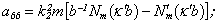 Equating the determinant (5) zero and opening him, we receive the characteristic equation for wave numbers of form m of three-dimensional flexural waves in a isotropic cylindrical shell of any (but constant) thickness.The decision of the characteristic equation for steel and aluminium shells of various thickness is submitted in a fig. 2 and 3, thus external radius was accepted equal 1,0, and radius b accepted two meanings: b = 0,99 (continuous curve) and b = 0,8 (dotted curve). The meanings of velocities longitudinal (С1), lateral (С2) and Relay‘s wave (СR) are shown on the diagrams. The meaning m = 1 corresponds to zero form of flexural wave, which velocity aspires asimptoticaly to velocity of Relay‘s wave СR , Λ - length of a longitudinal wave in the shell’s material;
Equating the determinant (5) zero and opening him, we receive the characteristic equation for wave numbers of form m of three-dimensional flexural waves in a isotropic cylindrical shell of any (but constant) thickness.The decision of the characteristic equation for steel and aluminium shells of various thickness is submitted in a fig. 2 and 3, thus external radius was accepted equal 1,0, and radius b accepted two meanings: b = 0,99 (continuous curve) and b = 0,8 (dotted curve). The meanings of velocities longitudinal (С1), lateral (С2) and Relay‘s wave (СR) are shown on the diagrams. The meaning m = 1 corresponds to zero form of flexural wave, which velocity aspires asimptoticaly to velocity of Relay‘s wave СR , Λ - length of a longitudinal wave in the shell’s material; 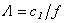 , where f - frequency of a wave in Hz. In a fig. 2 the phase velocities of three-dimensional flexural waves in steel shells, in a fig. 3 - in aluminium shells are shown.
, where f - frequency of a wave in Hz. In a fig. 2 the phase velocities of three-dimensional flexural waves in steel shells, in a fig. 3 - in aluminium shells are shown. 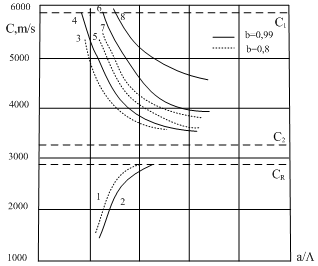 | Figure 2. Phase velocities of three-dimensional flexural waves in steel shells |
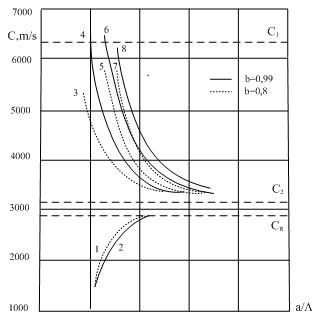 | Figure 3. Phase velocities of three-dimensional flexural waves in aluminum shells |
Let’s turn to axis-symmetrical longitudinal and flexural waves. In accordance with[5 – 15] in axis-symmetrical case the boundary conditions (2) - (4) become simpler: the condition (3) disappears and the condition (2) takes the following form (in this case the index m=0 or 1):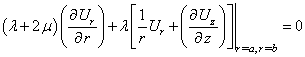 | (6) |
The determinant of the fourth order derived from boundary conditions takes the form[5]*: | (7) |
where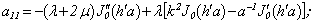
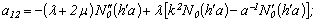
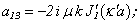
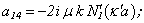
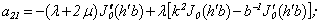
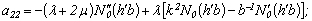
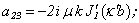
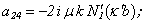
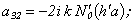 * In the present work the derivatives of cylindrical functions at radial coordinate r are marked the following way:
* In the present work the derivatives of cylindrical functions at radial coordinate r are marked the following way: 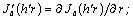
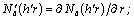 in the work[5] differently:
in the work[5] differently: 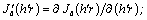
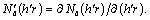 Both approaches are competent.
Both approaches are competent.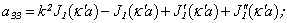
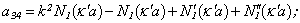
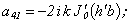
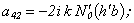
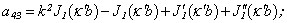
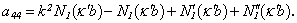 Equating the determinant (7) zero and opening it, we get the characteristic equation for wave numbers of flexural and longitudinal axis-symmetrical waves. The determinant for axis-symmetrical torsion waves are represented in[5]:
Equating the determinant (7) zero and opening it, we get the characteristic equation for wave numbers of flexural and longitudinal axis-symmetrical waves. The determinant for axis-symmetrical torsion waves are represented in[5]: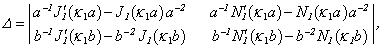 | (8) |
where 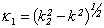 , k - is the desired wave number of axis-symmetrical torsion wave in the shell.Equating the determinant (8) zero and opening it, we get the characteristic equation for wave numbers of axis-symmetrical torsion waves.
, k - is the desired wave number of axis-symmetrical torsion wave in the shell.Equating the determinant (8) zero and opening it, we get the characteristic equation for wave numbers of axis-symmetrical torsion waves.
3. The Results of Numerical Experiment for Determination of Phase Velocities of Elastic Waves
The second part of the article investigates the results of numerical experiment for determination of phase velocities of elastic waves (axis-symmetrical and three-dimensional) in cylindrical shell and analyses the calculated dependences. The results of calculations of phase velocities are represented in the fig.4.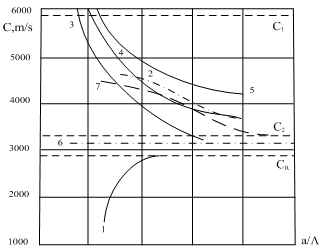 | Figure 4. Phase velocities of axis-symmetrical flexural, longitudinal and torsion waves in steel cylindrical shell |
One can find the following designations in the picture: the curve 1 - is the phase velocity of zero mode of flexural wave; the curve 2 - is the phase velocity of zero mode of longitudinal wave; the curves 3, 4, 5 - are the phase velocities of nonzero modes of longitudinal or of flexural waves; the straight line 6 - is the phase velocity of zero mode of torsion wave; the curve 7 - is the phase velocity of the first mode of torsion wave: 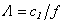 . In order to define the influence of external and internal liquid mediums on dispersion curves of phase velocities of shell to the determinant of the sixth order (5) are added two columns and two lines and it converts into the determinant of the eight order, and determinant of the fourth order– into the determinant of the sixth order. The potentials of sound waves (in external environment) and in the filling of the shell expand by the cylindrical functions the following way:
. In order to define the influence of external and internal liquid mediums on dispersion curves of phase velocities of shell to the determinant of the sixth order (5) are added two columns and two lines and it converts into the determinant of the eight order, and determinant of the fourth order– into the determinant of the sixth order. The potentials of sound waves (in external environment) and in the filling of the shell expand by the cylindrical functions the following way: 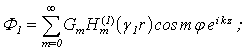 | (9) |
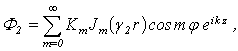 | (10) |
where: 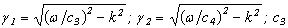 and
and 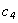 - sound velocities in external and internal environments correspondingly.The component of wave vector lengthwise of axis
- sound velocities in external and internal environments correspondingly.The component of wave vector lengthwise of axis 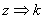 , as in the shell in the force of Snellius law.In this case the boundary conditions (2) for normal tensions on the both surfaces of the shell transforms:
, as in the shell in the force of Snellius law.In this case the boundary conditions (2) for normal tensions on the both surfaces of the shell transforms: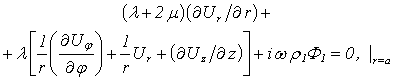 | (11) |
where: 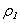 - the solidity of the external environment.
- the solidity of the external environment.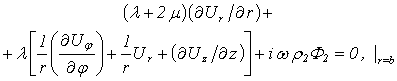 | (12) |
where: 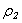 - the solidity of the internal environment. Two more boundary conditions are added: the normal components of displacement vector are continuous in the both borders of the shell:
- the solidity of the internal environment. Two more boundary conditions are added: the normal components of displacement vector are continuous in the both borders of the shell: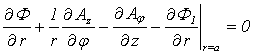 | (13) |
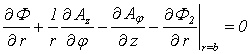 | (14) |
In axis-symmetrical case the condition (6) transforms: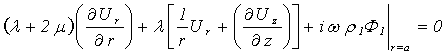 | (15) |
 | (16) |
The added boundary conditions in axis-symmetrical case: | (17) |
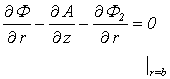 | (18) |
In axis-symmetrical case: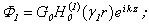 | (19) |
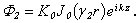 | (20) |
The boundary conditions (11), (12) and (17), (18) will add two lines to determinant, and the multipliers of unknown coefficients 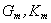 or
or 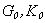 (axis-symmetrical problem) will add two columns. In this case only two lines in each of these two columns will be different from zero. If the shell borders the liquid only from one side (and from the other is still the vacuum) the determinant for determination of wave numbers will have the seventh order in three-dimensional problem and the fifth order (in axis-symmetrical case), that is to determinants (5) и (7) one line and one column are added correspondingly.The results presented in the article are received in the conducting of scientific research in the framework of State contract P 242 from 23 April 2010 FPP (Scientific and scientific - pedagogical personnel of innovative Russia for the years 2009-2013).
(axis-symmetrical problem) will add two columns. In this case only two lines in each of these two columns will be different from zero. If the shell borders the liquid only from one side (and from the other is still the vacuum) the determinant for determination of wave numbers will have the seventh order in three-dimensional problem and the fifth order (in axis-symmetrical case), that is to determinants (5) и (7) one line and one column are added correspondingly.The results presented in the article are received in the conducting of scientific research in the framework of State contract P 242 from 23 April 2010 FPP (Scientific and scientific - pedagogical personnel of innovative Russia for the years 2009-2013).
4. Conclusions
Based on use of Debye’s potentials one can find the direct solution of the problem of definition of the characteristic equation for phase velocities of three – dimensional flexural waves. The numerical solution of this equation destinates to obtain the dispersive curves of phase velocities. The dispersive dependencies of phase velocities of axis – symmetrical flexural, longitudinal and torsion waves are represented.
References
| [1] | Debye P. Ann. Phys. 30, 755 (1909). |
| [2] | Fock V. A. Elektromagnetic Diffraction and Propagation Problems (Sov. Radio, Moscow, 1970; Pergamon Oxford, 1965). |
| [3] | Kleshchev A. A. The Debye’s potentials and «the potentials of Debye’s type» in the problems of diffraction, radiation and spreading of elastic waves.// Acoustical journal. 2012. V. 58. № 3, P.338-341. |
| [4] | Kleshchev A. A., Klukin I.I. About of the flexural waves in elastic cylindrical bar. // Proceedings of Saint-Petersburg State Navy Technical University. v. 109. 1976. P. 24 – 28. |
| [5] | Ilmenkov S. L., Kleshchev A. A. Phase velocities of flexural waves in isotropic cylindrical shell of any thickness (strict decision) // Proceedings of the X Session of the Russian Acoustical Society. - 2001, v.1, Moscow. GEOS. P. 239-241. |
| [6] | Kleshchev A. A. Diffraction and propagation of waves in the elastic mediums and bodies.// Saint-Petersburg: Vlas, 2002. P. 156 . |
| [7] | Kleshchev A. A. The dispersive equations of displacement vectors of different modes of elastic waves in isotropic and anisotropic cylindrical shells. // Proceedings of the XIII Session of the Russian Acoustical Society.- 2003. М.: GEOS. P. 255 – 257. |
| [8] | Kleshchev A. A. The sound diffraction for point sound source in elastic cylindrical shells.// Acoustical journal.. 2004. V. 50. № 1. P. 86 – 89. |
| [9] | Ilmenkov S. L., Kleshchev A. A. Surgailo K.A. The phase velocities of elastic waves in bars and shells.// // Proceedings of the Regional scientific conference «The shipbuilding education and science» – 2003». Publ.house of the Saint-Petersburg State Navy Technical University, 2003. V. 1. P. 285 – 289. |
| [10] | Ilmenkov S. L., Kleshchev A. A. Physical model of sound radiation under action of the turbulent pulsations. // Proceedings of the Scientific conference «Bubnov’s lectures». Publ. house of the Krylov shipbuilding research institute. Saint-Petersburg. 2004. P. 102 – 103. |
| [11] | Kleshchev A. A. Diffraction, radiation and propagation of elastic waves.// Saint-Petersburg.:Profprint, 2006. P.160. |
| [12] | Kleshchev A. A. Experimental scattering characteristics of low – frequency non-fixed sound signal for elastic cylindrical shells in Frenel’s zone. // Proceedings of the XXI Session of the Russian Acoustical Society.-2009. М.: GEOS.. P. 163 – 166. |
| [13] | Kleshchev A. A., Legusha F.F., Maslov V. L. Wave process in the solids.//Saint-Petersburg. Publ. house of the Saint-Petersburg State Navy Technical University, 2010. P.216. |
| [14] | Kleshchev A. A. Scattering of Low – Frequency Pulsed Sound Signals from Elastic Cylindrical Shells. // Acoustical Physics. 2011. V. 57. № 3. P. 375 –380. |
| [15] | Kleshchev A. A. Acoustic Scatterers .//The second publication. Saint-Petersburg. Prima, 2012. P. 267. |


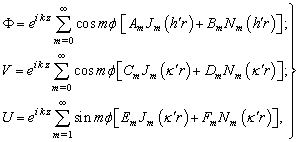
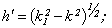
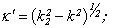
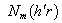 - are the Naman’s cylindrical function; Am , Bm , Cm , Dm , Em , Fm - are the unknown coefficients of expanding, which are calculated basing on the following physical boundary conditions on the external
- are the Naman’s cylindrical function; Am , Bm , Cm , Dm , Em , Fm - are the unknown coefficients of expanding, which are calculated basing on the following physical boundary conditions on the external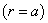 and inside
and inside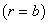 surfaces of the shell: there are no normal and tangent tensions on the both boundaries of the shell.We desire the analytical form of boundary conditions as following:
surfaces of the shell: there are no normal and tangent tensions on the both boundaries of the shell.We desire the analytical form of boundary conditions as following:
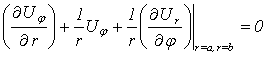
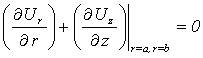

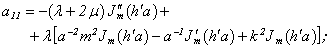
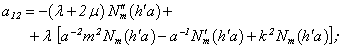
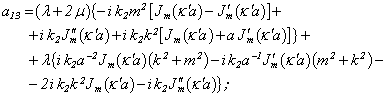
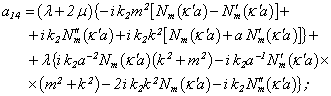
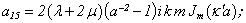
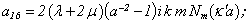
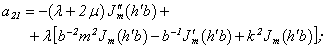
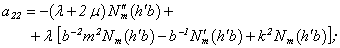
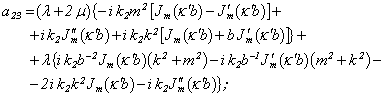
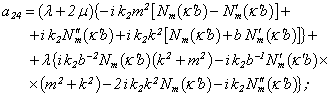
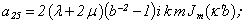
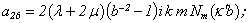
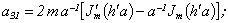
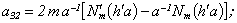
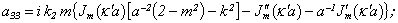
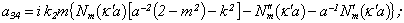
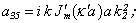
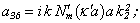
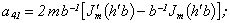
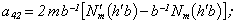
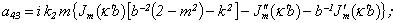
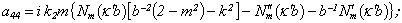
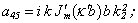
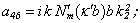
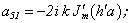
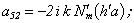
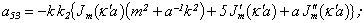
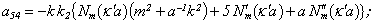
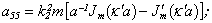
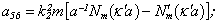
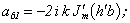
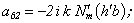
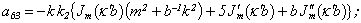
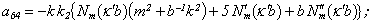
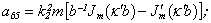
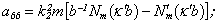 Equating the determinant (5) zero and opening him, we receive the characteristic equation for wave numbers of form m of three-dimensional flexural waves in a isotropic cylindrical shell of any (but constant) thickness.The decision of the characteristic equation for steel and aluminium shells of various thickness is submitted in a fig. 2 and 3, thus external radius was accepted equal 1,0, and radius b accepted two meanings: b = 0,99 (continuous curve) and b = 0,8 (dotted curve). The meanings of velocities longitudinal (С1), lateral (С2) and Relay‘s wave (СR) are shown on the diagrams. The meaning m = 1 corresponds to zero form of flexural wave, which velocity aspires asimptoticaly to velocity of Relay‘s wave СR , Λ - length of a longitudinal wave in the shell’s material;
Equating the determinant (5) zero and opening him, we receive the characteristic equation for wave numbers of form m of three-dimensional flexural waves in a isotropic cylindrical shell of any (but constant) thickness.The decision of the characteristic equation for steel and aluminium shells of various thickness is submitted in a fig. 2 and 3, thus external radius was accepted equal 1,0, and radius b accepted two meanings: b = 0,99 (continuous curve) and b = 0,8 (dotted curve). The meanings of velocities longitudinal (С1), lateral (С2) and Relay‘s wave (СR) are shown on the diagrams. The meaning m = 1 corresponds to zero form of flexural wave, which velocity aspires asimptoticaly to velocity of Relay‘s wave СR , Λ - length of a longitudinal wave in the shell’s material; 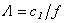 , where f - frequency of a wave in Hz. In a fig. 2 the phase velocities of three-dimensional flexural waves in steel shells, in a fig. 3 - in aluminium shells are shown.
, where f - frequency of a wave in Hz. In a fig. 2 the phase velocities of three-dimensional flexural waves in steel shells, in a fig. 3 - in aluminium shells are shown. 

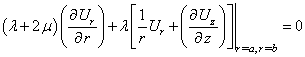

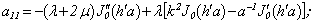
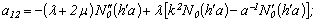
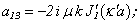
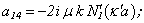
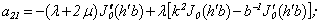
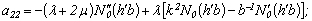
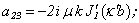
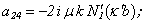
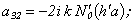 * In the present work the derivatives of cylindrical functions at radial coordinate r are marked the following way:
* In the present work the derivatives of cylindrical functions at radial coordinate r are marked the following way: 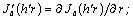
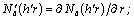 in the work[5] differently:
in the work[5] differently: 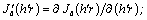
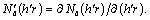 Both approaches are competent.
Both approaches are competent.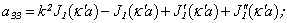
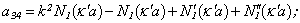
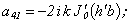
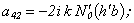
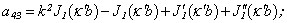
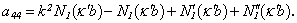 Equating the determinant (7) zero and opening it, we get the characteristic equation for wave numbers of flexural and longitudinal axis-symmetrical waves. The determinant for axis-symmetrical torsion waves are represented in[5]:
Equating the determinant (7) zero and opening it, we get the characteristic equation for wave numbers of flexural and longitudinal axis-symmetrical waves. The determinant for axis-symmetrical torsion waves are represented in[5]: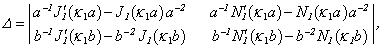
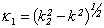 , k - is the desired wave number of axis-symmetrical torsion wave in the shell.Equating the determinant (8) zero and opening it, we get the characteristic equation for wave numbers of axis-symmetrical torsion waves.
, k - is the desired wave number of axis-symmetrical torsion wave in the shell.Equating the determinant (8) zero and opening it, we get the characteristic equation for wave numbers of axis-symmetrical torsion waves. 
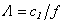 . In order to define the influence of external and internal liquid mediums on dispersion curves of phase velocities of shell to the determinant of the sixth order (5) are added two columns and two lines and it converts into the determinant of the eight order, and determinant of the fourth order– into the determinant of the sixth order. The potentials of sound waves (in external environment) and in the filling of the shell expand by the cylindrical functions the following way:
. In order to define the influence of external and internal liquid mediums on dispersion curves of phase velocities of shell to the determinant of the sixth order (5) are added two columns and two lines and it converts into the determinant of the eight order, and determinant of the fourth order– into the determinant of the sixth order. The potentials of sound waves (in external environment) and in the filling of the shell expand by the cylindrical functions the following way: 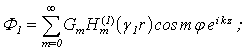
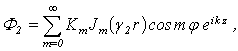
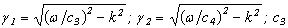 and
and 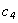 - sound velocities in external and internal environments correspondingly.The component of wave vector lengthwise of axis
- sound velocities in external and internal environments correspondingly.The component of wave vector lengthwise of axis 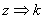 , as in the shell in the force of Snellius law.In this case the boundary conditions (2) for normal tensions on the both surfaces of the shell transforms:
, as in the shell in the force of Snellius law.In this case the boundary conditions (2) for normal tensions on the both surfaces of the shell transforms: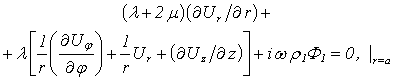
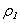 - the solidity of the external environment.
- the solidity of the external environment.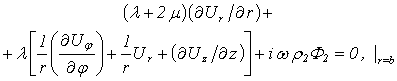
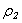 - the solidity of the internal environment. Two more boundary conditions are added: the normal components of displacement vector are continuous in the both borders of the shell:
- the solidity of the internal environment. Two more boundary conditions are added: the normal components of displacement vector are continuous in the both borders of the shell: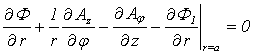
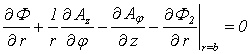
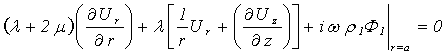


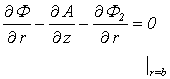
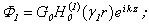
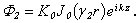
 or
or 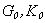 (axis-symmetrical problem) will add two columns. In this case only two lines in each of these two columns will be different from zero. If the shell borders the liquid only from one side (and from the other is still the vacuum) the determinant for determination of wave numbers will have the seventh order in three-dimensional problem and the fifth order (in axis-symmetrical case), that is to determinants (5) и (7) one line and one column are added correspondingly.The results presented in the article are received in the conducting of scientific research in the framework of State contract P 242 from 23 April 2010 FPP (Scientific and scientific - pedagogical personnel of innovative Russia for the years 2009-2013).
(axis-symmetrical problem) will add two columns. In this case only two lines in each of these two columns will be different from zero. If the shell borders the liquid only from one side (and from the other is still the vacuum) the determinant for determination of wave numbers will have the seventh order in three-dimensional problem and the fifth order (in axis-symmetrical case), that is to determinants (5) и (7) one line and one column are added correspondingly.The results presented in the article are received in the conducting of scientific research in the framework of State contract P 242 from 23 April 2010 FPP (Scientific and scientific - pedagogical personnel of innovative Russia for the years 2009-2013). Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML