-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2012; 2(6): 187-195
doi: 10.5923/j.ijtmp.20120206.03
Entanglement between Two Tavis-Cummings Systems with N=2
Seyed Arash Ghoreishi , Mohsen Sarbishaei , Kourosh Javidan
Department of Physics, Ferdowsi university of Mashhad, Mashhad, 91775-1436, Iran
Correspondence to: Seyed Arash Ghoreishi , Department of Physics, Ferdowsi university of Mashhad, Mashhad, 91775-1436, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
We consider two non interacting two-atoms Tavis-Cummings systems and examine the entanglement among four two-state atoms. For our purpose, we assume that one atom from each system are entangled initially and we obtain time-dependent concurrence among atoms. There are six pairwise concurrences among atoms and in this paper, we focus on remote atoms. We show that initially non-entangled atoms 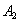 and
and 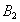 becomes entangled by passing time, the process which may be interpreted as entanglement transfer between the cavities.
becomes entangled by passing time, the process which may be interpreted as entanglement transfer between the cavities.
Keywords: Entanglement, Tavis-Cummings Model, Concurrence
Cite this paper: Seyed Arash Ghoreishi , Mohsen Sarbishaei , Kourosh Javidan , "Entanglement between Two Tavis-Cummings Systems with N=2", International Journal of Theoretical and Mathematical Physics, Vol. 2 No. 6, 2012, pp. 187-195. doi: 10.5923/j.ijtmp.20120206.03.
Article Outline
1. Introduction
- Entanglement is one of the most fascinating aspect of quantum mechanics and is a defining future that makes fundamental distinctions between quantum and classical Physics. Two quantum systems A and B are entangled when values of certain properties of system A are correlated with the same properties of system B[1]. Quantum entanglement has been viewed as an essential resources for quantum information process, and a great deal of effort has been devoted to study and characterize the entanglement. Cavity quantum electrodynamics (QED) techniques has been recognized as a promising candidate for the physical realization of quantum information processing[2]. In this paper we consider two non interacting two-atoms Tavis-Cummings systems and examine the entanglement among four two-states atoms by obtaining the concurrences between each two atoms. The method which we have used is like the method that is used in ref[3]. For this purpose we first introduce the Tavis-Cummings model and then obtain the eigenvalues and eigenstates of the two-atoms Tavis-Cummings system in section 2. These eigenstates and eigenvalues are used for calculating the time evaluation of entanglement. We introduce the concept of concurrence for measuring the entanglement in section 3 and finally in section 4, we analyze the entanglement among atoms in detail by calculating the reduced density matrice of each two two-levels atoms and give some concludes in section 5.
2. The Tavis-Cummings Model
- The Tavis-Cummings model (TCM) describes the simplest fundamental interaction between a single mode of the quantized electromagnetic field and a collection of N two-level atoms under the rotating wave approximation approximation (RWA) condition[4] -[11]. The Hamiltonian of this model is written as
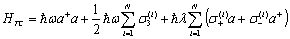 | (1) |
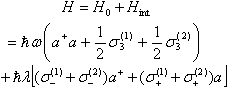 | (2) |
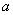 and
and 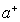 are the annihilation and creation field operators.Each initial state in this system is coupled to three states. For example if the initial state is
are the annihilation and creation field operators.Each initial state in this system is coupled to three states. For example if the initial state is 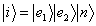 then this state is coupled with the states
then this state is coupled with the states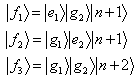 | (3) |
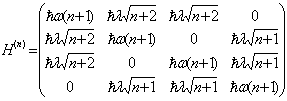 | (4) |
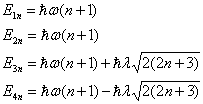 | (5) |
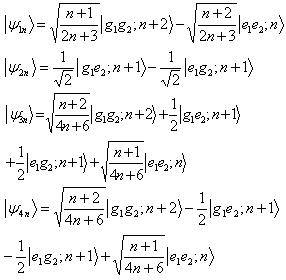
3. Measure of Entanglement
- To measure the entanglement, we need to introduce a convenient concept. We will adopt the Wooter's concurrence[13] as our measure:
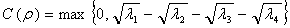 | (7) |
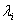 are the eigenvalues in decreasing order of the matrix
are the eigenvalues in decreasing order of the matrix 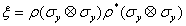 | (8) |
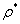 denotes the complex conjugation of
denotes the complex conjugation of 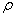 in the standard basis and
in the standard basis and 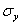 is the Pauli matrix.We may pay attention to this point that although the matrix
is the Pauli matrix.We may pay attention to this point that although the matrix 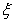 is not Hermitian, the eigenvalues of this matrix are real and nonnegative.Note that
is not Hermitian, the eigenvalues of this matrix are real and nonnegative.Note that 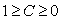 , where
, where 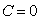 indicates zero entanglement and
indicates zero entanglement and 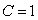 means maximal pure state entanglement.Reduction to a two-qubit form, will yield to a two-qubit mixed state always having the form:
means maximal pure state entanglement.Reduction to a two-qubit form, will yield to a two-qubit mixed state always having the form: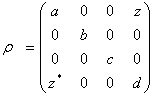 | (9) |
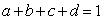 . The concurrence for this matrix is easily found to be
. The concurrence for this matrix is easily found to be 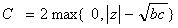 | (10) |
4. Entanglement Dynamics among Atoms in Two Tavis-Cummings Systems with N=2
- Consider two two-atoms Tavis-Cummings systems A and B where A consists of two atoms
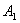 ,
,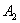 and B consists of two atoms
and B consists of two atoms 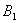 ,
,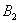 . We assume that initially an atom of system A,
. We assume that initially an atom of system A, 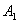 ,is entangled with an atom of system B,
,is entangled with an atom of system B, 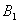 Now, we are going to investigate the entanglement among atoms in this two Tavis-Cummings systems by calculating the concurrence among atoms. The total initial state has three parts:i) The entangled atoms: This initial part can be written in terms of Bell states. We denote this part as follows:
Now, we are going to investigate the entanglement among atoms in this two Tavis-Cummings systems by calculating the concurrence among atoms. The total initial state has three parts:i) The entangled atoms: This initial part can be written in terms of Bell states. We denote this part as follows: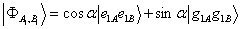 | (11) |
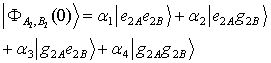 | (12) |
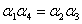 | (13) |
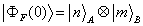 | (14) |
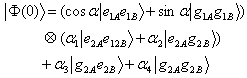 | (15) |
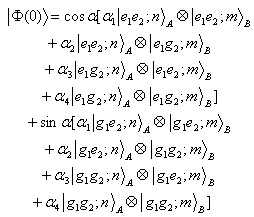 | (16) |
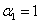 ,
,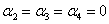 ) and the number of photons in two cavities are equal (n=m). By applying these conditions, the initial state becomes
) and the number of photons in two cavities are equal (n=m). By applying these conditions, the initial state becomes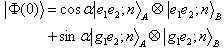 | (17) |
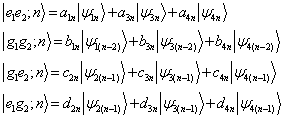 | (18) |
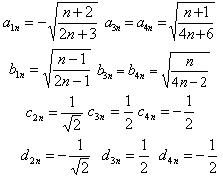 | (19) |
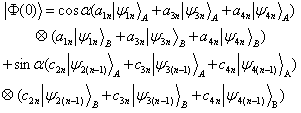 | (20) |
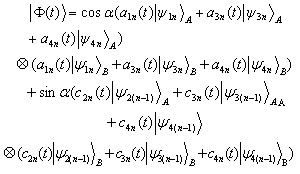 | (21) |
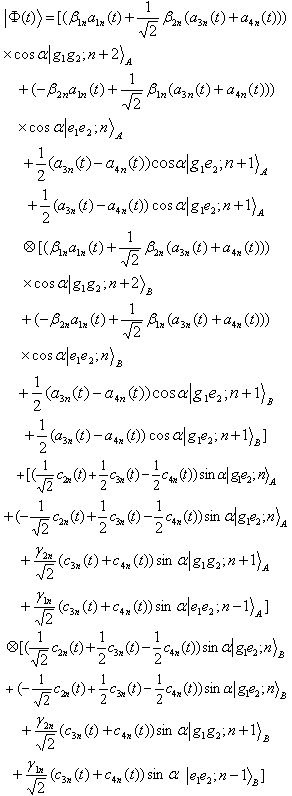 | (22) |
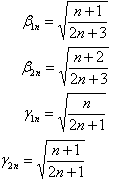 | (23) |
 by trace out from density operator on the photonic states
by trace out from density operator on the photonic states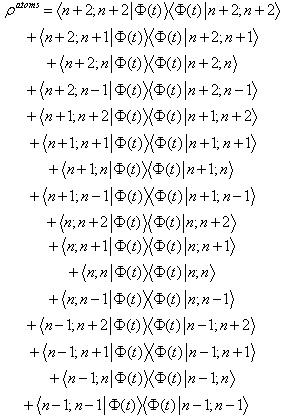 | (24) |
 we can obtain the reduced density matrix between each two atoms.We first focus on
we can obtain the reduced density matrix between each two atoms.We first focus on 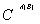 . This requires that we trace out
. This requires that we trace out 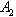 and
and 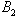 atom states, in order to get the two-qubit mixed state needed for calculation at
atom states, in order to get the two-qubit mixed state needed for calculation at 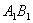 concurrence. The
concurrence. The 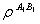 becomes
becomes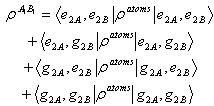 | (25) |
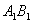 mixed state has the form
mixed state has the form 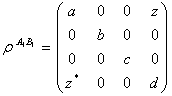 | (26) |
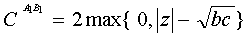 | (27) |
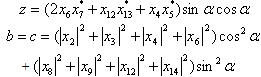 | (28) |
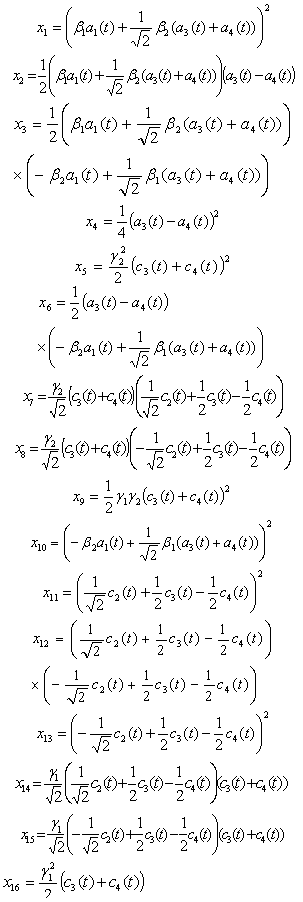 | (29) |
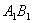 mixed state. In these graphs
mixed state. In these graphs 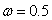 ,
,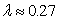 and
and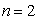 .
. 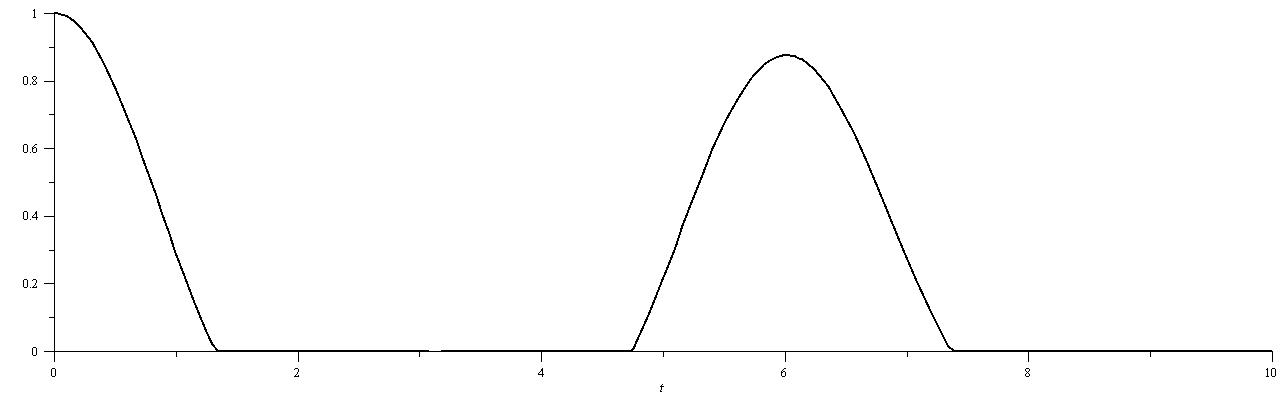 | Figure 1. plot of 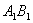 concurrence for concurrence for 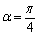 |
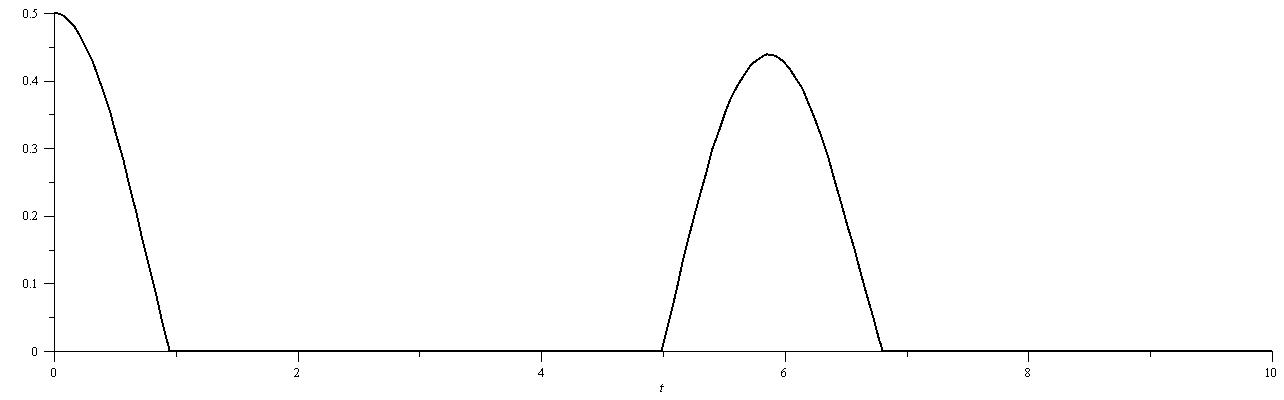 | Figure 2. plot of 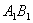 concurrence for concurrence for 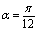 |
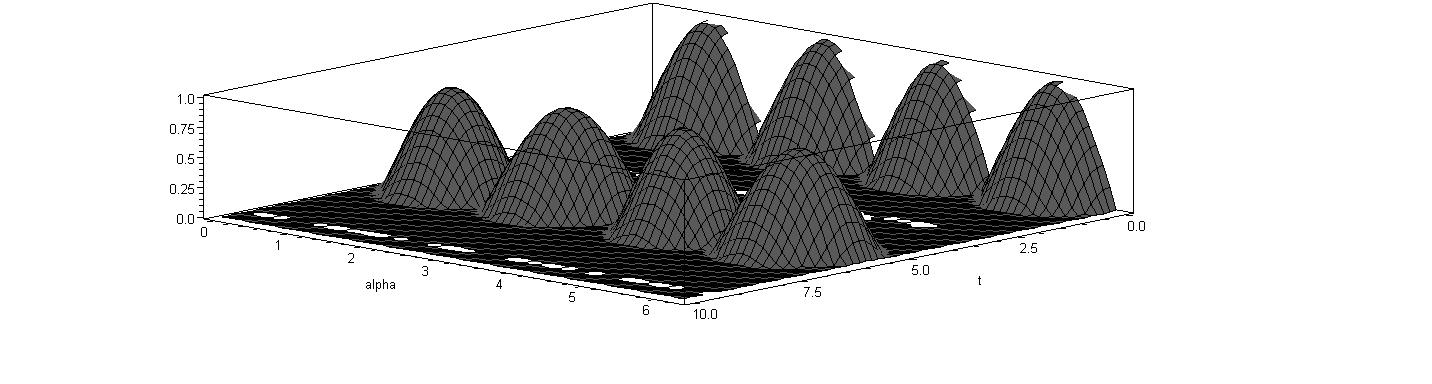 | Figure 3. Surface plot of the concurrence |
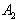 and
and 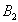 :
: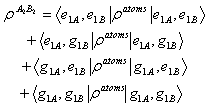 | (30) |
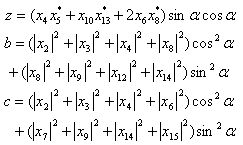 | (31) |
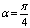 and
and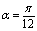 at the first 100 seconds.
at the first 100 seconds.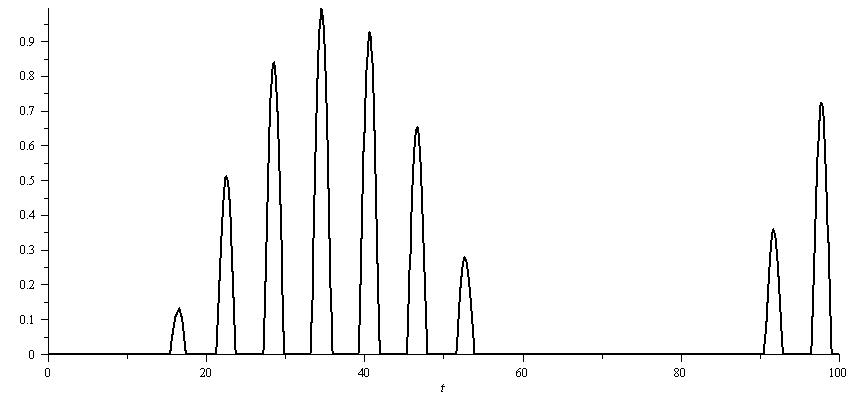 | Figure 4. plot of 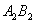 concurrence for concurrence for 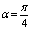 |
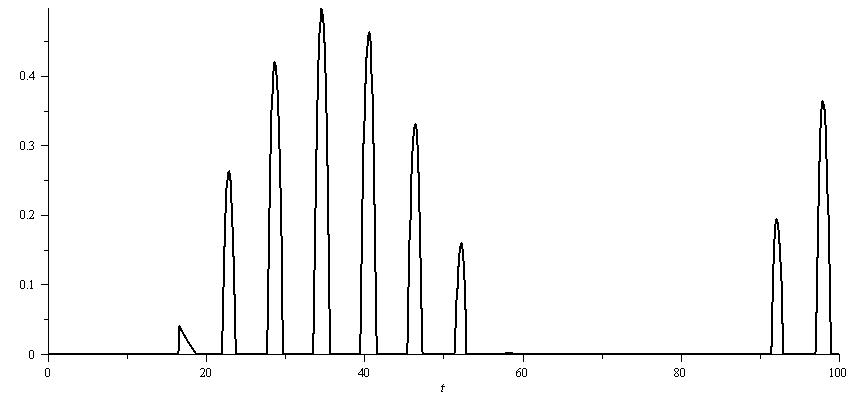 | Figure 5. plot of 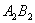 concurrence for concurrence for 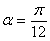 |
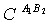 and
and 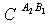 . We start with
. We start with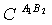 . For this, we trace out
. For this, we trace out 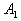 and
and 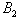 .
.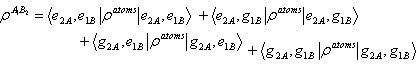 | (32) |
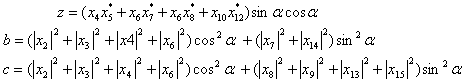 | (33) |
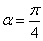 and
and 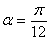 at the first 100 seconds.If we look at the initial state in equation (19) we see that under the transformation
at the first 100 seconds.If we look at the initial state in equation (19) we see that under the transformation 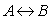 the state remain unchanged. That means
the state remain unchanged. That means 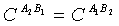 at all times.Similarly, we can find the explicit expressions for
at all times.Similarly, we can find the explicit expressions for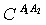 and
and 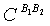 . The two cavities are not distinguishable, so we expect these C's to be the same and they are. The
. The two cavities are not distinguishable, so we expect these C's to be the same and they are. The 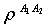 has the form
has the form 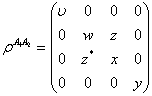 | (34) |
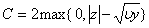 | (35) |
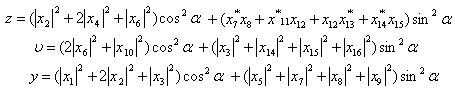 | (36) |
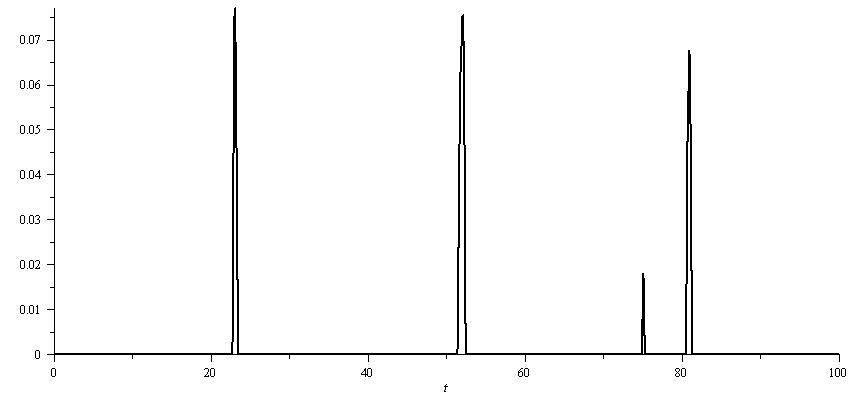 | Figure 6. plot of 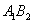 concurrence for concurrence for 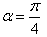 |
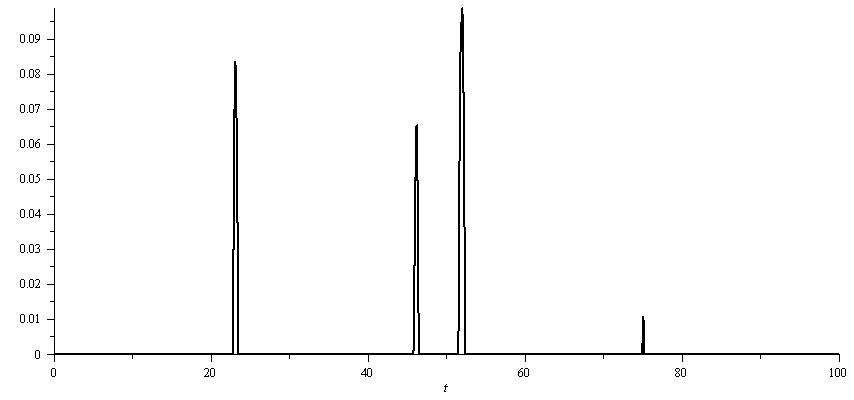 | Figure 7. plot of 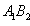 concurrence for concurrence for 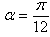 |
5. Conclusions
- In this paper we considered two two-atoms Tavis-Cummings systems. These two systems have no interaction together, but one atom from each system are entangled initially (
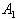 ,
,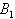 ).The entanglement between
).The entanglement between 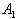 and
and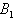 for times t>0 falls to zero and remains non-entangled for a period of time till becomes entangled again. We also see that the entangled intervals are smaller than non-entangled intervals. For initially non-entangled atoms,
for times t>0 falls to zero and remains non-entangled for a period of time till becomes entangled again. We also see that the entangled intervals are smaller than non-entangled intervals. For initially non-entangled atoms, 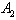 and
and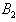 , the entanglement appears in short intervals. But the entanglement between
, the entanglement appears in short intervals. But the entanglement between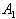 and
and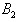 or
or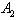 and
and 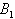 is very negligible in very short intervals; therefore, we can claim that these atoms will not be entangled afterwards.We can test other initial states in our problem. For example for two initially entangled atoms, we can use another initially state
is very negligible in very short intervals; therefore, we can claim that these atoms will not be entangled afterwards.We can test other initial states in our problem. For example for two initially entangled atoms, we can use another initially state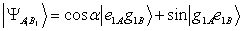 | (37) |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML