S. L. Ilmenkov , A. A. Kleshchev
Saint-Petersburg State Navy Technical University, Saint-Petersburg, Lotsmanskaya st.,3, 190008, Russia
Correspondence to: A. A. Kleshchev , Saint-Petersburg State Navy Technical University, Saint-Petersburg, Lotsmanskaya st.,3, 190008, Russia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Are studied internal and external tasks of radiation of a sound by the elastic bodies, exciting by the harmonic point source, imitating turbulent pulsation of a flow of a liquid. The angular characteristics of radiation of a hollow spheroidal shell are calculated. The characteristic equations of the axial three-dimensional flexural waves in the hollow cylindrical shell and cylindrical bar are received with the help of Debye’s potentials. The phase velocities of the various forms of these waves for shells and for cylindrical bar are calculated.
Keywords:
Turbulence, Flexural Wave, Longitudinal Wave, Radiation of the Sound, Phase Velocity
Cite this paper:
S. L. Ilmenkov , A. A. Kleshchev , "The Debye’s Potentials Utilization in the Three-Dimensional Problems of the Radiation and Propagation of the Elastic Waves", International Journal of Theoretical and Mathematical Physics, Vol. 2 No. 6, 2012, pp. 163-169. doi: 10.5923/j.ijtmp.20120206.01.
1. Introduction
At study of the three-dimensional characteristics of radiation of a sound by the elastic shells and bars exciting by the turbulent pulsation of a flow of a liquid and calculation of the phase velocities of the axial flexural waves in such bodies at such excitation it is necessary to use an artificial way of division variable in Helmholtz vector equation for a vector function 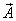 - to present her through Debye’s potentials or “such as Debye’s” potentials.
- to present her through Debye’s potentials or “such as Debye’s” potentials.
2. The Radiation of a Sound by the Cylindrical and Spheroidal Shells, Exciting by the Turbulent Pulsation of a Flow of a Liquid
Firstly we will consider a physical model of radiation of a sound by a cylindrical pipe (an internal task) and spheroidal shell (an external task), which is raised by turbulent pulsations of a liquid flow.In a monograph[1], devoted to the studying of the hydrodynamic sources of a sound, it is noted that for the range of problems regarding the radiations of a sound effected by turbulent pulsations of a liquid flow, the calculation, based on the concentrated force, caused by this pulsation, gives rise to certain interest.. The similar physical model is used in a present article. Such approach is based on the earlier obtained results in the course of authors’ research of the three-dimensional problems of diffraction and radiation of a sound by the elastic bodies of cylindrical and spheroidal forms[2 - 5].Let’s turn to an internal task for the consideration of: the harmonic point source 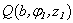 of frequency ω, that imitate turbulent pulsation, is found on the interior of the shell
of frequency ω, that imitate turbulent pulsation, is found on the interior of the shell 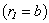 , but the point of observation Р with the cylindrical coordinates
, but the point of observation Р with the cylindrical coordinates 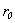 ,
, 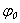 ,
, 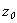 is situated inside of a liquid flow
is situated inside of a liquid flow 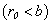 (figure 1):
(figure 1):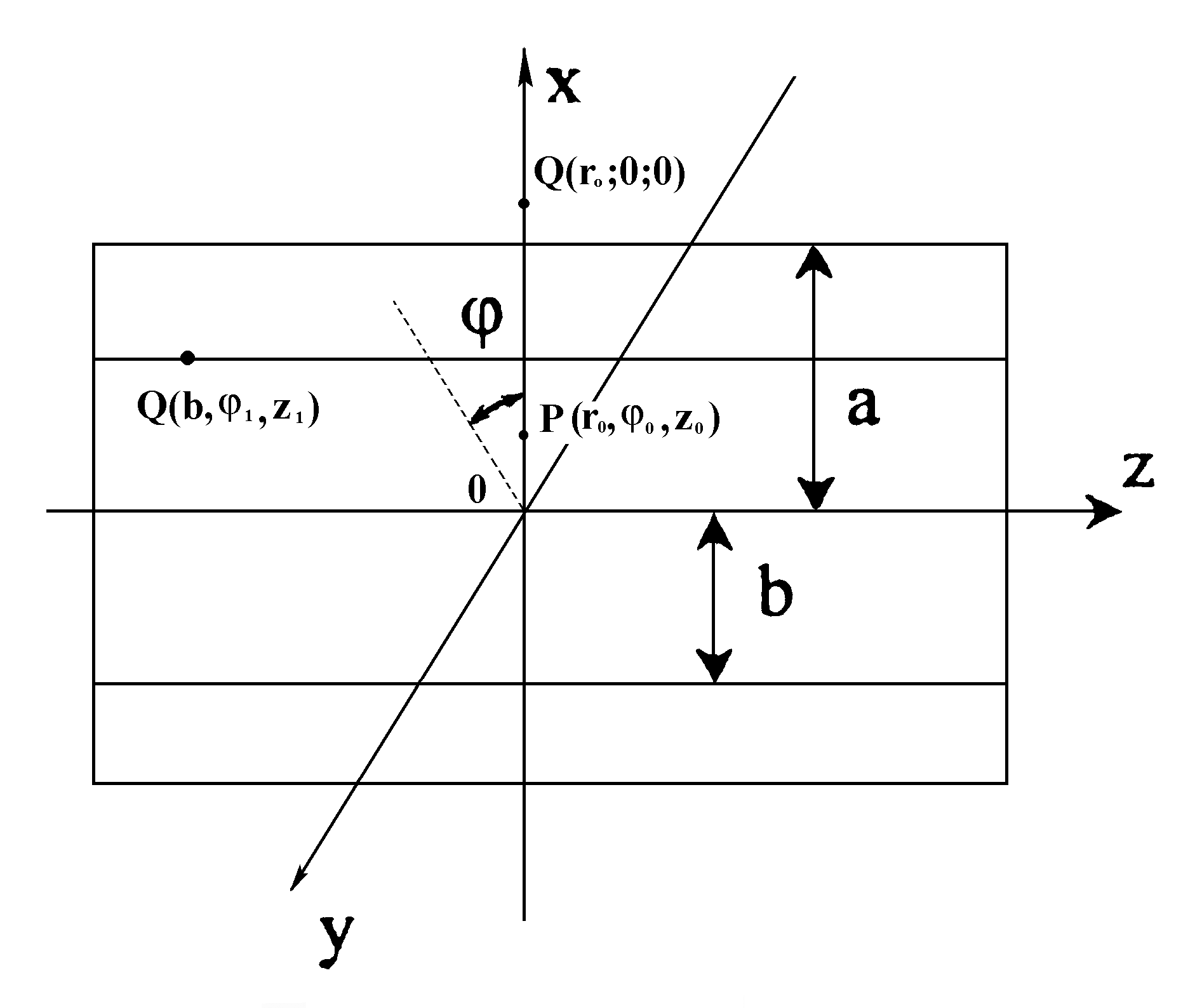 | Figure 1. The isotropic cylindrical shell, exciting from within by a point harmonic source |
The external radius of the cylindrical pipe 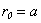 , on the outside region to the shell
, on the outside region to the shell 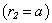 is the vacuum. In order to except the presence of the source (a peculiarity) on the boundary surface, we use a reciprocity theorem (6) and trade places a source Q and a point of observation P. As a result the formulation of the task will be the following: we will search potential
is the vacuum. In order to except the presence of the source (a peculiarity) on the boundary surface, we use a reciprocity theorem (6) and trade places a source Q and a point of observation P. As a result the formulation of the task will be the following: we will search potential 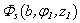 in point Q of an internal border, resulting of the dispersion by pipe of a sound from dot source with potential
in point Q of an internal border, resulting of the dispersion by pipe of a sound from dot source with potential 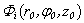 placed in a point P, basing on[5, 7]. The potential
placed in a point P, basing on[5, 7]. The potential 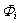 of the harmonic point source in a point Q is defined by the series[8 - 10]:
of the harmonic point source in a point Q is defined by the series[8 - 10]: | (1) |
where:  ;
;  - is the sound velocity; γ and
- is the sound velocity; γ and 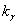 - are the axial and radial components of a wave vector
- are the axial and radial components of a wave vector 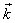 correspondingly;
correspondingly; 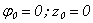 (figure 1);
(figure 1);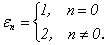 By analogy with
By analogy with 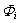 in a point Q, a potential of the diffused wave shell
in a point Q, a potential of the diffused wave shell 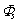 can be written as[7, 5, 11]:
can be written as[7, 5, 11]: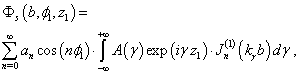 | (2) |
where 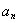 and
and 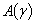 - are unknown coefficients and functions of γ correspondingly and they are determined by the boundary conditions. The cylindrical components of a displacement vector
- are unknown coefficients and functions of γ correspondingly and they are determined by the boundary conditions. The cylindrical components of a displacement vector 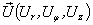 can be written by way of potential Ф and the cylindrical components of a function
can be written by way of potential Ф and the cylindrical components of a function 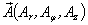 [12-14]:
[12-14]: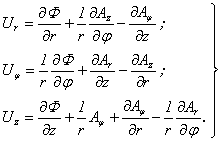 | (3) |
The cylindrical components 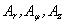 of the function
of the function 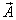 can be described by way of Debye’s potentials U and V[5, 12 - 16]:
can be described by way of Debye’s potentials U and V[5, 12 - 16]: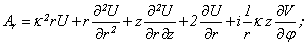 | (4) |
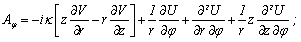 | (5) |
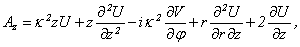 | (6) |
where: κ–the wave number of the lateral wave in the shell’s material;A vector function 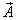 is are described by Debye’s potentials U and V[12 - 16]:
is are described by Debye’s potentials U and V[12 - 16]: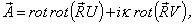 | (7) |
where: 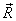 - is a radius-vector of view point.The efficiency of such representation becomes obvious if we take into account, that the functions U and V submit to the Helmholtz scalar equation, divided in circular cylindrical coordinates:
- is a radius-vector of view point.The efficiency of such representation becomes obvious if we take into account, that the functions U and V submit to the Helmholtz scalar equation, divided in circular cylindrical coordinates: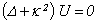 | (8) |
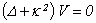 | (9) |
The other representations for a vector function 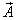 in the Cartesian and cylindrical coordinate systems are given in[17 - 19], but it is[5] in a spheroidal system. The potentials Φ, U and V are also expanded in serieses by eigen-functions of the Helmholtz scalar equation[16, 5, 11]:
in the Cartesian and cylindrical coordinate systems are given in[17 - 19], but it is[5] in a spheroidal system. The potentials Φ, U and V are also expanded in serieses by eigen-functions of the Helmholtz scalar equation[16, 5, 11]: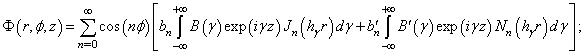 | (10) |
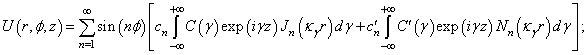 | (11) |
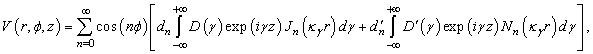 | (12) |
где: 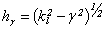 ;
; 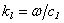 - is a longitudinal wave number;
- is a longitudinal wave number; 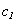 - is a longitudinal wave velocity in the shell’s material;
- is a longitudinal wave velocity in the shell’s material; 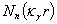 - Neiman’s cylindrical;
- Neiman’s cylindrical; 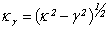 ;
; 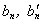 ,
,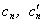 ,
,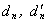 и
и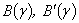 ,
,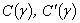 ,
,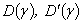 - are unknown coefficients and functions correspondingly and they are determined by the next boundary conditions at the external and internal surfaces of an elastic shell:1) a normal component of a displacement vector
- are unknown coefficients and functions correspondingly and they are determined by the next boundary conditions at the external and internal surfaces of an elastic shell:1) a normal component of a displacement vector 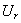 is continuous at an internal shell’s boundary; 2) a sound pressure in a fluid is equal to the normal strain in a shell at an internal boundary; 3) a normal strain in a shell at an external boundary is equal to zero; 4) the tangent strains at the shell’s boundaries are equal to zero.An analytic form of the enumerated boundary conditions are a following representation:
is continuous at an internal shell’s boundary; 2) a sound pressure in a fluid is equal to the normal strain in a shell at an internal boundary; 3) a normal strain in a shell at an external boundary is equal to zero; 4) the tangent strains at the shell’s boundaries are equal to zero.An analytic form of the enumerated boundary conditions are a following representation: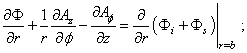 | (13) |
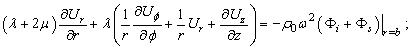 | (14) |
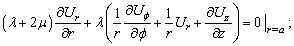 | (15) |
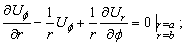 | (16) |
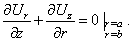 | (17) |
A substitution of the series (1), (2), (10) - (12) in the boundary conditions (13) - (17) results in an infinite system of the equations to define the unknown coefficients and functions 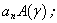 ,
, 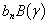 ,
, 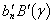 ,
, 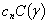 ,
, 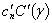 ,
, 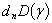 ,
, 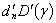 . As the trigonometrical functions cos(nφ) and sin(nφ) are opthogonal, an infinite system breaks out into seven equation with fixed index n for finding the seven combinations of the unknown coefficients and functions.A product
. As the trigonometrical functions cos(nφ) and sin(nφ) are opthogonal, an infinite system breaks out into seven equation with fixed index n for finding the seven combinations of the unknown coefficients and functions.A product 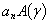 for a potential of a diffused wave
for a potential of a diffused wave 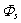 is calculated by the Cramer rule on a basis of a ratio of the who determinants of the seven degree:
is calculated by the Cramer rule on a basis of a ratio of the who determinants of the seven degree: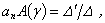 | (18) |
where: Δ – is determinant of a system, but 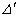 -is minor;
-is minor;

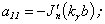
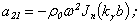
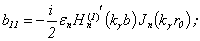
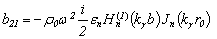 The rest of elements of the rows and columnes of a determinants Δ и
The rest of elements of the rows and columnes of a determinants Δ и can be taken out[5]. Except for the first column elements Δ and
can be taken out[5]. Except for the first column elements Δ and  - identical.An influence of a turbulent pulsation at a prolate spheroidal shell is considered as an external problem. At figure 2 is show hollow spheroidal shell, by streamline flow of a liquid. The points А, В, С mark the possible positions of a point source, imitating turbulent pulsation. With help[2 - 4], can be calculated the angular characteristics of a radiation of a spheroidal shell under an influence of a turbulent pulsation.
- identical.An influence of a turbulent pulsation at a prolate spheroidal shell is considered as an external problem. At figure 2 is show hollow spheroidal shell, by streamline flow of a liquid. The points А, В, С mark the possible positions of a point source, imitating turbulent pulsation. With help[2 - 4], can be calculated the angular characteristics of a radiation of a spheroidal shell under an influence of a turbulent pulsation. 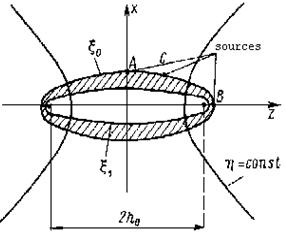 | Figure 2. The isotropic prolate spheroidal shell, exciting on the outside by a point harmonic source |
At figures 3 and 4 are shown the modulus of the angular characteristics of a radiation 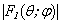 this shell by an excitement in a point В (figure 3) and point А (figure 4).
this shell by an excitement in a point В (figure 3) and point А (figure 4). 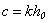 is a wave dimension of a body,
is a wave dimension of a body, 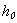 - is a half of an interfocus distance (figure 2). A figure 3 corresponds С=8,1, but a figure 4 – С=5,5.
- is a half of an interfocus distance (figure 2). A figure 3 corresponds С=8,1, but a figure 4 – С=5,5.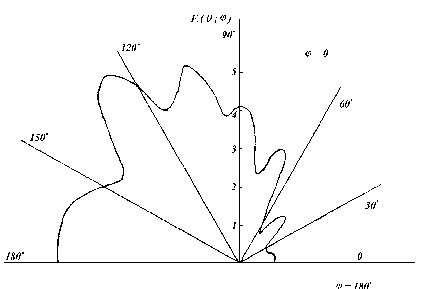 | Figure 3. The modulus of an angular characteristic of a radiation 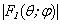 hollow spheroidal shell, exciting on the exciting on the outside by a point harmonic source in a point В; С=8,1 hollow spheroidal shell, exciting on the exciting on the outside by a point harmonic source in a point В; С=8,1 |
A dipole character of a radiation of a turbulent pulsation[1] can foresee an introduction of a second source (with an other sign), disposed at a small from a first source, and to calculate in a point of observation total pressure from two sources. By an use of a reciprocity theorem a transference of a turbulent pulsation Q together with a flow of a fluid along of an internal surface of a shell (figure 1) is substituted for a transference of a point of observation P parallel to a boundary in a opposite direction. 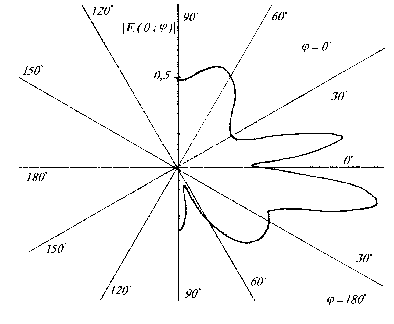 | Figure 4. The modulus of an angular characteristic of a radiation 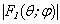 of a steel of a steel hollow spheroidal shell, outside by a point harmonic source in a point A; С=5,5 of a steel of a steel hollow spheroidal shell, outside by a point harmonic source in a point A; С=5,5 |
3. The Phase Velocities of Three-Dimensional Flexural Waves in Cylindrical Shells and Bars
Further we shall proceed to consideration of phase velocities of one of types of waves existing in cylindrical shells and bars: axial three-dimensional flexural waves. Wave of a similar type were in detail investigated in[5, 15, 20 - 28]. The characteristic equation for wave numbers of three-dimensional flexural waves of form m in the isotropic cylindrical shell it turns out by equating to zero of the determinant of six order[5, 15, 23, 25, 27, 28]: | (19) |
where : а11 = - (λ + 2μ) Jm11(h1a) + λ[a-2m2Jm(h1a) - a-1Jm1(h1a)+ k2 Jm(h1a)]; а12 = - (λ + 2μ) Nm11(h1a) + λ[a-2m2Nm(h1a) - a-1Nm1(h1a)+ k2 Nm(h1a)];а 13 = (λ + 2μ){-iχm2[ Jm(χ1a) - Jm1(χ1a)] + iχ Jm11(χ1a) + iχk2[Jm(χ1a) + a Jm1(χ1a)]} + λ{ iχa-2 Jm(χ1a)( m2 + k2) - iχa-1 Jm1(χ1a) ( m2 + k2) - 2iχ k2 Jm(χ1a) - iχ Jm11(χ1a)};а 14 = (λ + 2μ){-iχm2[ Nm(χ1a) - Nm1(χ1a)] + iχ Nm11(χ1a) + iχk2[Nm(χ1a) + a Nm1(χ1a)]} + λ{ iχa-2 Nm(χ1a)( m2 + k2) - iχa-1 Nm1(χ1a) ( m2 + k2) - - 2iχ k2 Nm(χ1a) - iχ Nm11(χ1a)};а 15 = 2(λ + 2μ)( a-2-1)ikm Jm(χ1a); а 16 = 2(λ + 2μ)( a-2-1)ikm Nm(χ1a);а21 = - (λ + 2μ) Jm11(h1b) + λ[b-2m2Jm(h1b) - b-1Jm1(h1b)+ k2 Jm(h1b)];а22 = - (λ + 2μ) Nm11(h1b) + λ[b-2m2Nm(h1b) - b-1Nm1(h1b)+ k2 Nm(h1b)];а 23 = (λ + 2μ){-iχm2[ Jm(χ1b) - Jm1(χ1b)] + iχ Jm11(χ1b) + iχk2[Jm(χ1b) + b Jm1(χ1b)]} + λ{ iχb-2 Jm(χ1b)( m2 + k2) - iχb-1 Jm1(χ1b) ( m2 + k2) - 2iχ k2 Jm(χ1b) - iχ Jm11(χ1b)};а 24 = (λ + 2μ){-iχm2[ Nm(χ1b) - Nm1(χ1b)] + iχ Nm11(χ1b) + iχk2[Nm(χ1b) + b Nm1(χ1b)]} + λ{ iχb-2 Nm(χ1b)( m2 + k2) - iχb-1 Nm1(χ1b) ( m2 + k2) - 2iχ k2 Nm(χ1b) - iχ Nm11(χ1b)};а 25 = 2(λ + 2μ)( b-2-1)ikm Jm(χ1b); а 26 = 2(λ + 2μ)( b-2-1)ikm Nm(χ1b);а 31 = 2ma-1[Jm1(h1a) - a-1Jm(h1a)];а 32 = 2ma-1[Nm1(h1a) - a-1Nm(h1a)];а 33 = iχm{ Jm(χ1a)[ a-2 (2- m2) - k2] - Jm11(χ1a) - a-1 Jm1(χ1a) };а 34 = iχm{ Nm(χ1a)[ a-2 (2- m2) - k2] - Nm11(χ1a) - a-1 Nm1(χ1a) };a35 = ikJm1(χ1a)aχ2 ; a36 = ikNm1(χ1a)aχ2 ;а 41 = 2mb-1[Jm1(h1b) - b-1Jm(h1b)]; а 42 = 2mb-1[Nm1(h1b) - b-1Nm(h1b)];а 43 = iχm{ Jm(χ1b)[ b-2 (2- m2) - k2] - Jm11(χ1b) - b-1 Jm1(χ1b) };а 44 = iχm{ Nm(χ1b)[ b-2 (2- m2) - k2] - Nm11(χ1b) - b-1 Nm1(χ1b) };a45 = ikJm1(χ1b)bχ2 ; a46 = ikNm1(χ1b)bχ2 ;а 51 = -2ik Jm1(h1a); а 52 = -2ik Nm1(h1a);а 53 = - kχ[ Jm(χ1a)(m2 + a-1k2) + 5 Jm1(χ1a) + aJm11(χ1a)];а 54 = - kχ[ Nm(χ1a)(m2 + a-1k2) + 5 Nm1(χ1a) + aNm11(χ1a)];а 55 = χ2m[a-1Jm(χ1a) - Jm1(χ1a)]; а 56 = χ2m[a-1Nm(χ1a) - Nm1(χ1a)];а 61 = -2ik Jm1(h1b); а 62 = -2ik Nm1(h1b);а 63 = - kχ[Jm(χ1b)(m2 + b-1k2) + 5 Jm1(χ1b) + bJm11(χ1b)];а 64 = - kχ[ Nm(χ1b)(m2 + b-1k2) + 5 Nm1(χ1b) + bNm11(χ1b)];а 65 = χ2m[b-1Jm(χ1b) - Jm1(χ1b)]; а 66 = χ2m[b-1Nm(χ1b) - Nm1(χ1b)];In the figures 5 and 6 the results of calculations of phase velocities of three-dimensional flexural waves for steel and aluminium shells are represented. The following designations one can find : the curves 1, 2 corresponds m=1 (zero mode); the curves 3, 4- m = 2; the curves 5, 6 - m = 3; the curves 7, 8- m = 4; The external radius of shells and was accepted equal 1,0 m. С1 – the velocity of longitudinal wave ; СR - the velocity of Relay‘s wave; 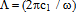 ; internal radius b = 0,99 м corresponds to a thin shell, b = 0,8 м – thick shell.The characteristic equation for wave numbers κ of three-dimensional flexural waves in the isotropic cylindrical bar of radius а =1,0, received with the help of Debye’s potentials, looks like[22, 26]:
; internal radius b = 0,99 м corresponds to a thin shell, b = 0,8 м – thick shell.The characteristic equation for wave numbers κ of three-dimensional flexural waves in the isotropic cylindrical bar of radius а =1,0, received with the help of Debye’s potentials, looks like[22, 26]: 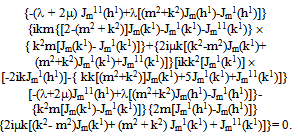 | (20) |
In the figure 7 the phase velocities of first three forms of flexural waves in the steel cylindrical bar, received with the help of “such as Debye’s” potentials, are represented.[19, 28].The the phase velocities of axissymmetrical flexural waves (longitudinal and torsional in bars, longitudinal, torsional and flexural in shells) are submitted in[5, 24, 26, 27, 28]. As to anisotropic of shells and bars, the jobs are devoted to phase velocities of elastic waves in them[18, 29, 30]. On known phase velocities the components of a vector of displacement of an elastic body in any point with the help of results of job can be calculated[31]. 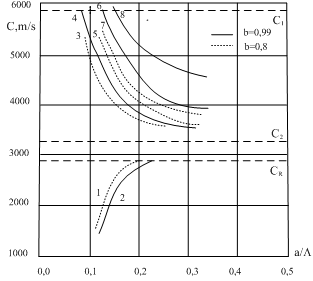 | Figure 5. The phase velocities of three-dimensional flexural waves in steel cylindrical shells |
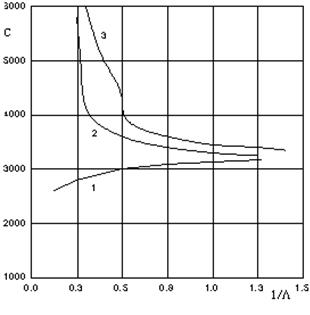 | Figure 6. The phase velocities of three- dimensional flexural waves in aluminium cylindrical shells |
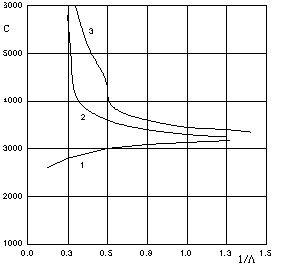 | Figure 7. The phase velocities of first three forms of flexural waves in the steel cylindrical bar |
4. Conclusions
The decision of a three-dimensional task of radiation of a sound by a cylindrical and spheroidal shells, which is raised by turbulent pulsations of a liquid flow is received. The characteristics of radiation by a spheroidal shell under action of such sources are calculated.The characteristic equations for wave numbers of the three-dimensional axial flexural waves, raised in an cylindrical shell and bar are received. The dispersive curves of phase velocities of the various forms of these waves for steel and aluminium shells of various thickness and for steel cylindrical bar are submitted.
References
| [1] | I. Ja. Miniovich, A.D.Pernik, V.S. Petrovsky. Hydrodynamical sources of sound. L.: Shipbuilding, 1972.P.480. |
| [2] | S.L. Ilmenkov, A.A. Kleshchev. Radiation elastic bodies spheroidal form and bond his with diffraction of sound. // Higher school collection. Ships acoustics. 1989. P.15-21. Leningrad shipbuilding institute. |
| [3] | S.L. Ilmenkov, A.A. Kleshchev, I.I. Klukin, S.B. Rumjantsev. Radiation of elastic spheroid under act of point source. // Higher school collection. Ships systems.1989.P.100-104. Leningrad shipbuilding institute. |
| [4] | A.A. Kleshchev. Hydroacoustic scatterers. // The second publication. Saint-Petersburg. Prima, 2012, P.267. Scientific&Academic Publishing (SAP). |
| [5] | A.A. Kleshchev. Diffraction and propagation of waves in elastic mediums and bodies. S-Pb.: Vlas. 2002. P.156. |
| [6] | L.M. Ljamshev. To question about principle of reciprocity. P.Ac.Sc. USSR. 1959.Т.125. P.1231-1234. |
| [7] | A.A. Kleshchev. Diffraction of sound radiated by a point source on an elastic cylindri cal shell. // J. of Techn. Acoust. 1997.V.3.N4.P.20-23. |
| [8] | E.L. Shenderov. Wave problems of hydroacoustic. L.: Shipbuilding, 1972.P.350. |
| [9] | L.M. Brehovskikh. Waves in flaky mediums. М.: Publ. House Ac.Sc. USSR, 1957. P.502. |
| [10] | L. Felsen, U.N. Markuvits. Radiation and scattering of waves. M.: World, 1978,V.1-2. |
| [11] | A.A. Kleshchev. Diffraction of sound by a point source on an elastic cylindrical shell. // Acoust. Journ. 2004. V.50. № 1. P.86-89. |
| [12] | Debye P. Das Verhalten von Lichtwellen in der Nähe eines Brennpunktes oder einer Brennlinie. //Ann. Physik. 1909.V.30.N4.S.755-776. |
| [13] | V.A. Fok. Problems of diffraction and propagation of electromagnetic waves. М.: Soviet radio, 1970. P.517. |
| [14] | A.A. Kleshchev, I.I. Klukin. About bend waves in elastic circular cylindrical bar. // Higer school collection. 109. P. 3-5. |
| [15] | A.A. Kleshchev. Against the phase velocities of flexural waves in cylindrical shell //J. of Techn. Acoust. 1997. V. 3. N4. P. 16 - 19. |
| [16] | A.A. Kleshchev. Diffraction of sound radiated by a point source on an elastic cylindrical shell // J. of Techn. Acoust. 1997. V. 3. N4. P. 20 - 23. |
| [17] | Buchwald V. T. Rayleich waves in transversely isotropic media. // Quart. Journ. Mech. and Applied. Math. 1961. V. XIV. Pt. 3. P. 293 - 317. |
| [18] | Ahmad F. Guided waves in a transversely isotropic cylinder immersed in a fluid. // J.A.S.A. 2001. V. 109. N3. P. 886 - 890. |
| [19] | Fan Y., Sinclair A. N., Honarvar F. Scattering of a plane acoustic wave from a transversely isotropic cylinder encased in a solid elasticmedium.//JASA.1999.V106.N3.Pt.1.P.1229-1236. |
| [20] | A.A., Kleshchev, I.I. Klukin. About bend waves in elastic cylindrical bar. // Higer school collection. 1975.109. P. 3-5. |
| [21] | A.A., Kleshchev, I.I. Klukin. Ships acoustics. L.: Shipbuilding, 1982. P.144. |
| [22] | S.L. Ilmenkov, A.A. Kleshchev, Phase velocities of bend wave of nonzero forms of thin elastic circular infinite cylindrical bar. // J.of Techn. Acoust. 1999. v.4. № 1. P.14-17. |
| [23] | S.L. Ilmenkov, A.A. Kleshchev, Phase velocities of bend wave of nonzero modes of elastic infinite cylindrical shell. // J.of Techn. Acoust. 1999. v.4. № 1. P.18-20. |
| [24] | S.L. Ilmenkov, A.A. Kleshchev, Phase Velocities of Flexural, Longitudinal and Torsional waves in isotropic cylindrical shell (the correct solution) // Proceedings of the X Session of the Russian Acoustical Society. M.: GEOS. 2000, V.1, P 210-214. |
| [25] | S.L. Ilmenkov, A.A. Kleshchev. Phase Velocities of Flexural waves in isotropic cylindrical shell of any thickness. // Proceedings of the X1 Session of the Russian Acoustical Society. M.: GEOS. 2001, V.1, P 239-241. |
| [26] | A.A. Kleshchev, K.A. Surgailo. Phase Velocities of elastic waves in isotropic cylindrical bar of any thickness. // Proceedings of the X1 Session of the Russian Acoustical Society. M.: GEOS. 2001, V.1, P. 236-238. |
| [27] | S.L. Ilmenkov, A.A. Kleshchev, K.A. Surgailo. Phase Velocities of elastic waves in bars and shells // Proceedings of the Sc. Conf. GMTU, S-Pb. 2003 (is not issuded). |
| [28] | A.A. Kleshchev. Debye’s and “such as Debye’s” potentials in the problems of diffraction, radiation and propagation of elastic waves // Proceedings of the V Int. Conf. «Morintech– 2003». 2003. V.2. S-Pb.: P.55-61. |
| [29] | А.А. Kleshchev. About phase velocities of elastic waves in thin axissymmetrical isotropic cylindrical shell. // Proceedings of the X Session of the Acoustic society of Russia. 2000. V.1. M.: GEOS.P.206-210. |
| [30] | А.А. Kleshchev. About phase velocities of elastic waves in thin ortotropic cylindrical shell. // Proceedings of the X Session of the Acoustic society of Russia.2001.V.1.М.: GEOS. P.241-244. |
| [31] | А.А. Kleshchev. Dispersion equations of a displacement vectors of differents forms of elastic waves in isotropic and anizotropic cylindrical shells.// Proceedings of the X111 Session of the Acoustic society of Russia.2003.V.1.М.: GEOS..P. 255-257. |

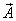 - to present her through Debye’s potentials or “such as Debye’s” potentials.
- to present her through Debye’s potentials or “such as Debye’s” potentials.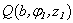 of frequency ω, that imitate turbulent pulsation, is found on the interior of the shell
of frequency ω, that imitate turbulent pulsation, is found on the interior of the shell 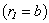 , but the point of observation Р with the cylindrical coordinates
, but the point of observation Р with the cylindrical coordinates 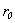 ,
, 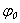 ,
, 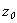 is situated inside of a liquid flow
is situated inside of a liquid flow 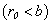 (figure 1):
(figure 1):
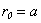 , on the outside region to the shell
, on the outside region to the shell 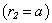 is the vacuum. In order to except the presence of the source (a peculiarity) on the boundary surface, we use a reciprocity theorem (6) and trade places a source Q and a point of observation P. As a result the formulation of the task will be the following: we will search potential
is the vacuum. In order to except the presence of the source (a peculiarity) on the boundary surface, we use a reciprocity theorem (6) and trade places a source Q and a point of observation P. As a result the formulation of the task will be the following: we will search potential 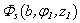 in point Q of an internal border, resulting of the dispersion by pipe of a sound from dot source with potential
in point Q of an internal border, resulting of the dispersion by pipe of a sound from dot source with potential 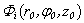 placed in a point P, basing on[5, 7]. The potential
placed in a point P, basing on[5, 7]. The potential 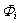 of the harmonic point source in a point Q is defined by the series[8 - 10]:
of the harmonic point source in a point Q is defined by the series[8 - 10]:
 ;
;  - is the sound velocity; γ and
- is the sound velocity; γ and 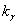 - are the axial and radial components of a wave vector
- are the axial and radial components of a wave vector 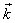 correspondingly;
correspondingly; 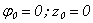 (figure 1);
(figure 1);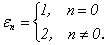 By analogy with
By analogy with 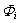 in a point Q, a potential of the diffused wave shell
in a point Q, a potential of the diffused wave shell  can be written as[7, 5, 11]:
can be written as[7, 5, 11]:
 and
and 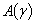 - are unknown coefficients and functions of γ correspondingly and they are determined by the boundary conditions. The cylindrical components of a displacement vector
- are unknown coefficients and functions of γ correspondingly and they are determined by the boundary conditions. The cylindrical components of a displacement vector 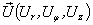 can be written by way of potential Ф and the cylindrical components of a function
can be written by way of potential Ф and the cylindrical components of a function 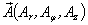 [12-14]:
[12-14]: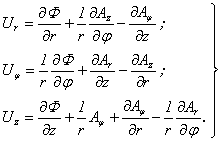
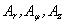 of the function
of the function 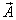 can be described by way of Debye’s potentials U and V[5, 12 - 16]:
can be described by way of Debye’s potentials U and V[5, 12 - 16]: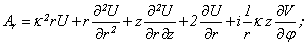
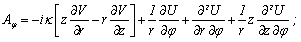
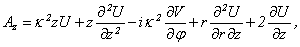
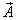 is are described by Debye’s potentials U and V[12 - 16]:
is are described by Debye’s potentials U and V[12 - 16]: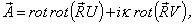
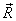 - is a radius-vector of view point.The efficiency of such representation becomes obvious if we take into account, that the functions U and V submit to the Helmholtz scalar equation, divided in circular cylindrical coordinates:
- is a radius-vector of view point.The efficiency of such representation becomes obvious if we take into account, that the functions U and V submit to the Helmholtz scalar equation, divided in circular cylindrical coordinates: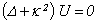
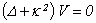
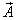 in the Cartesian and cylindrical coordinate systems are given in[17 - 19], but it is[5] in a spheroidal system. The potentials Φ, U and V are also expanded in serieses by eigen-functions of the Helmholtz scalar equation[16, 5, 11]:
in the Cartesian and cylindrical coordinate systems are given in[17 - 19], but it is[5] in a spheroidal system. The potentials Φ, U and V are also expanded in serieses by eigen-functions of the Helmholtz scalar equation[16, 5, 11]: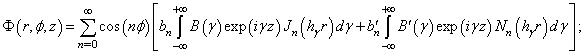
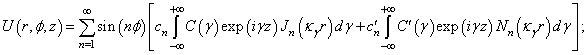
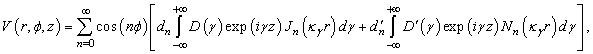
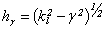 ;
; 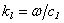 - is a longitudinal wave number;
- is a longitudinal wave number; 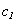 - is a longitudinal wave velocity in the shell’s material;
- is a longitudinal wave velocity in the shell’s material; 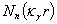 - Neiman’s cylindrical;
- Neiman’s cylindrical; 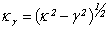 ;
; 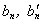 ,
,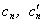 ,
,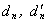 и
и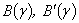 ,
,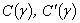 ,
,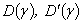 - are unknown coefficients and functions correspondingly and they are determined by the next boundary conditions at the external and internal surfaces of an elastic shell:1) a normal component of a displacement vector
- are unknown coefficients and functions correspondingly and they are determined by the next boundary conditions at the external and internal surfaces of an elastic shell:1) a normal component of a displacement vector 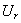 is continuous at an internal shell’s boundary; 2) a sound pressure in a fluid is equal to the normal strain in a shell at an internal boundary; 3) a normal strain in a shell at an external boundary is equal to zero; 4) the tangent strains at the shell’s boundaries are equal to zero.An analytic form of the enumerated boundary conditions are a following representation:
is continuous at an internal shell’s boundary; 2) a sound pressure in a fluid is equal to the normal strain in a shell at an internal boundary; 3) a normal strain in a shell at an external boundary is equal to zero; 4) the tangent strains at the shell’s boundaries are equal to zero.An analytic form of the enumerated boundary conditions are a following representation: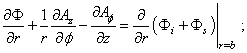
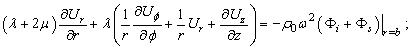
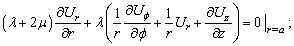
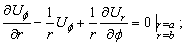
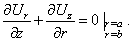
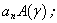 ,
, 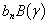 ,
, 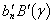 ,
, 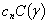 ,
, 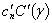 ,
, 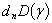 ,
, 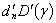 . As the trigonometrical functions cos(nφ) and sin(nφ) are opthogonal, an infinite system breaks out into seven equation with fixed index n for finding the seven combinations of the unknown coefficients and functions.A product
. As the trigonometrical functions cos(nφ) and sin(nφ) are opthogonal, an infinite system breaks out into seven equation with fixed index n for finding the seven combinations of the unknown coefficients and functions.A product 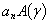 for a potential of a diffused wave
for a potential of a diffused wave 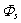 is calculated by the Cramer rule on a basis of a ratio of the who determinants of the seven degree:
is calculated by the Cramer rule on a basis of a ratio of the who determinants of the seven degree: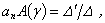
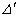 -is minor;
-is minor;

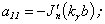
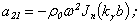
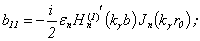
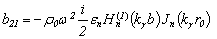 The rest of elements of the rows and columnes of a determinants Δ и
The rest of elements of the rows and columnes of a determinants Δ и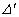 can be taken out[5]. Except for the first column elements Δ and
can be taken out[5]. Except for the first column elements Δ and 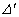 - identical.An influence of a turbulent pulsation at a prolate spheroidal shell is considered as an external problem. At figure 2 is show hollow spheroidal shell, by streamline flow of a liquid. The points А, В, С mark the possible positions of a point source, imitating turbulent pulsation. With help[2 - 4], can be calculated the angular characteristics of a radiation of a spheroidal shell under an influence of a turbulent pulsation.
- identical.An influence of a turbulent pulsation at a prolate spheroidal shell is considered as an external problem. At figure 2 is show hollow spheroidal shell, by streamline flow of a liquid. The points А, В, С mark the possible positions of a point source, imitating turbulent pulsation. With help[2 - 4], can be calculated the angular characteristics of a radiation of a spheroidal shell under an influence of a turbulent pulsation. 
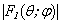 this shell by an excitement in a point В (figure 3) and point А (figure 4).
this shell by an excitement in a point В (figure 3) and point А (figure 4). 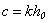 is a wave dimension of a body,
is a wave dimension of a body, 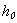 - is a half of an interfocus distance (figure 2). A figure 3 corresponds С=8,1, but a figure 4 – С=5,5.
- is a half of an interfocus distance (figure 2). A figure 3 corresponds С=8,1, but a figure 4 – С=5,5.
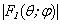 hollow spheroidal shell, exciting on the exciting on the outside by a point harmonic source in a point В; С=8,1
hollow spheroidal shell, exciting on the exciting on the outside by a point harmonic source in a point В; С=8,1
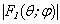 of a steel of a steel hollow spheroidal shell, outside by a point harmonic source in a point A; С=5,5
of a steel of a steel hollow spheroidal shell, outside by a point harmonic source in a point A; С=5,5
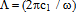 ; internal radius b = 0,99 м corresponds to a thin shell, b = 0,8 м – thick shell.The characteristic equation for wave numbers κ of three-dimensional flexural waves in the isotropic cylindrical bar of radius а =1,0, received with the help of Debye’s potentials, looks like[22, 26]:
; internal radius b = 0,99 м corresponds to a thin shell, b = 0,8 м – thick shell.The characteristic equation for wave numbers κ of three-dimensional flexural waves in the isotropic cylindrical bar of radius а =1,0, received with the help of Debye’s potentials, looks like[22, 26]: 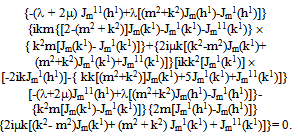



 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML