1. Introduction

In a recent paper[1] we have investigated a transmission line terminated by in series connected RCL-loads and we have reduced the mixed problem for the lossy transmission line equations to an initial value problem for a system of neutral equations on the boundary. Then we proved an existence-uniqueness result of periodic boundary value problem for the neutral system obtained but for one period. Global behaviour of the solution is declining rather than periodically. In contrast to parallel connected RCL-loads (cf.[2]) here the multiplier 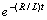could not be eliminated and this implies that the solution vanishes exponentially.

From the physical point of view this means that the signal vanishes in time. Moreover one can notice the voltage and current in the lossy transmission line are products of a periodic function and an exponential function, that is,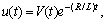

.

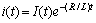Therefore 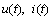should be oscillating functions and vanish exponentially at infinity. This suggest us to state the problem for an existence-uniqueness of a global oscillatory solution on 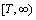vanishing exponentially at infinity. As in[1],[2] we assume the Heaviside condition is satisfied, that is,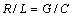. It implies that the transmission line is without distortion. Here we omit the reduction (cf.[1]) of the mixed problem for the hyperbolic system to a neutral system on the boundary and prove by the fixed point method (cf.[3]) an existence-uniqueness of the oscillatory solution for the neutral system. The main difficulty is generated by nonlinearities of RLC-loads (cf.[4]-[7]). We obtain successive approximation of the seeking oscillatory solution in an explicit form and estimate the rate of convergence.

Especially we want to draw attention to a fundamental disadvantage of lot of papers – solving equations without guaranteed uniqueness of the solution. Whatever the method (numerical, approximated and so on) to apply without uniqueness is not known to which of the many solutions are coming.

We mention recent various approaches for an analysis of transmission lines[8]-[15] .We would like to point out that we obtain an approximated solution but in explicit form beginning with simple functions.

2. Mixed Problem for the Lossy Transmission Line System terminated by in Series Connected RCL-Loads

We proceed from the lossy transmission line equations system:

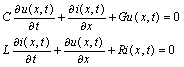(1)

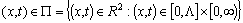with initial conditions

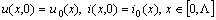(2)

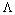where L, C, R and G are prescribed specific parameters of the line and >0 is its length and 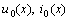are prescribed functions. Here 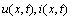are unknown functions – voltage and current respectively. The boundary conditions are derived from the loads and sources at the ends of the line (cf.[1], Fig. 1) on the base of Kirchoff’s laws.

For 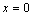we have

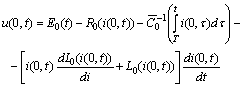(3)

and analogously for

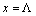
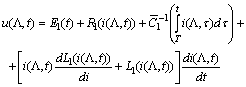(4)

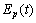where are the prescribed source functions and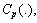 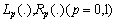are prescribed nonlinear functions – nonlinear characteristics of the corresponding elements.

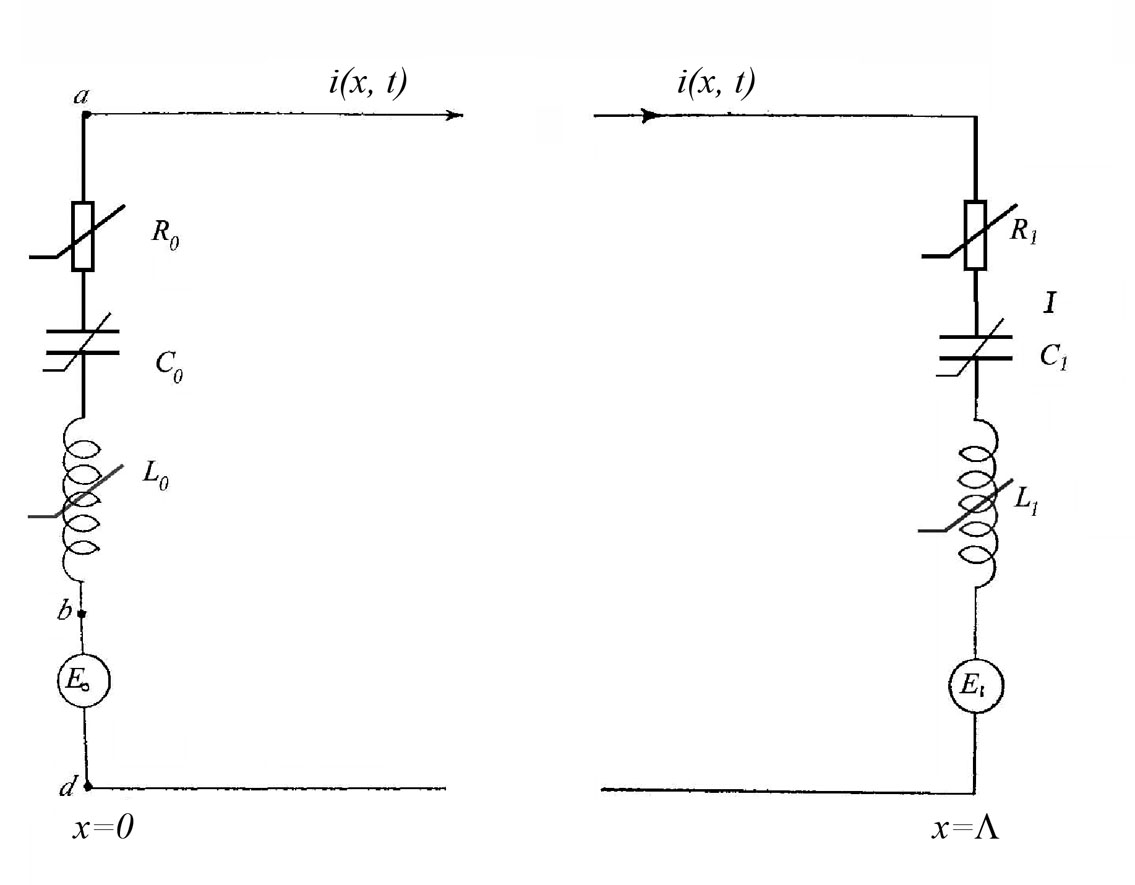Figure 1. Lossy transmission line terminated by nonlinear loads

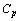Recall briefly some results from[1]. For the voltages of the condenser we proceed from the relation (assuming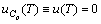, where ):

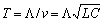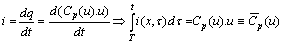and hence 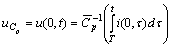, where

are constants. Since 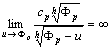and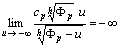 we conside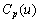r for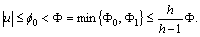

Since 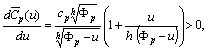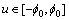, the inverse function 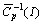exists and

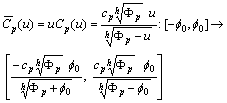that is,

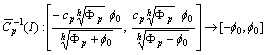and hence

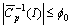(5)

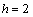The explicit form of the inverse function (for ) is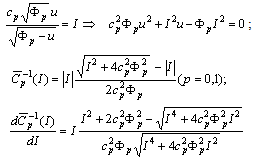

;

We need the following inequality:

.

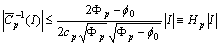We need also the following estimates:

;

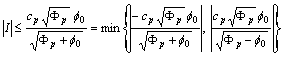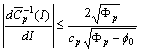(6)

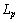The voltage of the inductor is

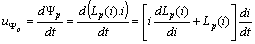where 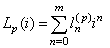and then

.

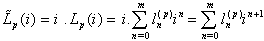We get

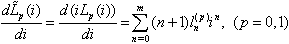We know that (cf.[4]-[7])

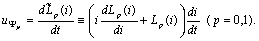For the I-V characteristics we assume that

.

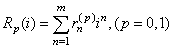The mixed problem (1)-(4) can be reduced to an initial value problem for a nonlinear neutral system. Recall some transformations from[1]:

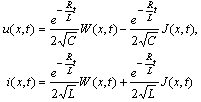which reduces (1) to the system

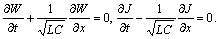(7)

The initial conditions remain unchanged because

.

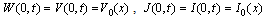Assume that the unknown functions are (cf.[1])

.

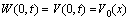and taking into account the relations obtained after integration along the characteristics

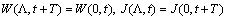we obtain the system (cf.[1]):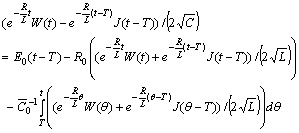

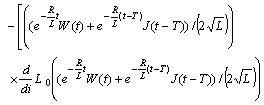
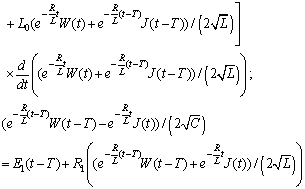
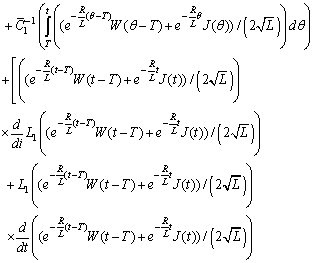Principal Remark. If 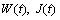are periodic functions then the functions 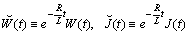should be oscillatory ones. They should satisfy the following inequalities 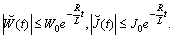Further on we again denote them by 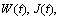that is,

.

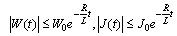So omitting some transformations given in details in[1] we reach the problem for existence-uniqueness of oscillatory solution 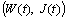of the following system: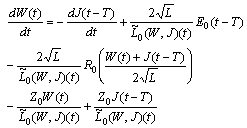

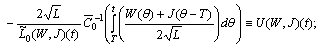
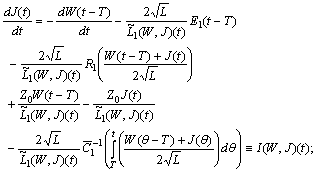
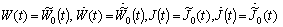(8)

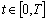where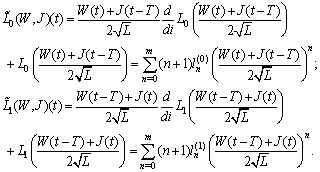

The initial functions are obtained as in[1].

First we formulate the conditions for the initial functions

(IN) .

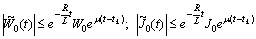Assume that one can find an interval 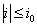such that the inequalities

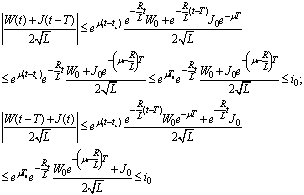(9)

imply

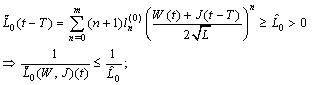
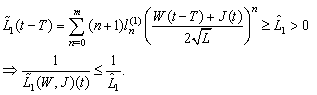This can be done if the polynomial has suitable properties (cf. Numerical example).

3. An Existence-Uniqueness of Oscillatory Solution for the Neutral System

Here we introduce an operator representation of the oscillatory problem and by a fixed point theorem in uniform spaces[3] we establish an existence-uniqueness of global oscillatory solution.

Now we are able to formulate the main problem: to find a solution of (8) with advanced prescribed zeros on an interval 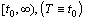where 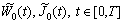are prescribed initial oscillating functions on the interval .

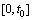Let 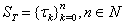(such that 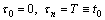) be the set of zeros of the initial functions, that is, .

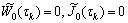Let 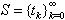be a strictly increasing sequence of real numbers satisfying the following conditions (C):

(C1) ;

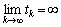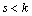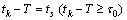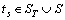(C2) for every k there is such that where .

(E) .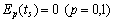

It follows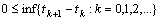

;

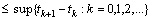
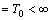Introduce the sets 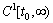consisting of all continuous and bounded functions differentiable with bounded derivatives on every interval .

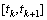Remark 3.1. Let us note that the left and right derivative at 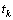of any 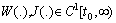may not coincide. This requires introducing of uniform spaces[3] with a suitable topology for continuous functions with piece wise continuous derivatives.

Introduce the sets

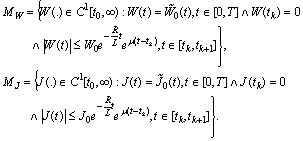Remark 3.2. Conditions (C2) and (E) imply that if 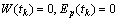then .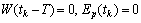

Remark 3.3. Let us comment the conformity condition (CC). It could be obtained replacing 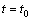in (8) and in view of 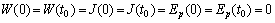and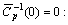

,

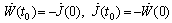where 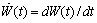. We notice that (CC) becomes a relation between the initial functions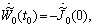 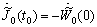. If the last condition is not satisfied then the jump of the derivative at 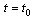propagates to the right and it falls at some zero point because of 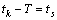. We do not go beyond our function space because the derivative of our functions might have jumps at .

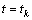Remark 3.4. It follows that the functions from 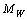and 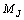satisfy the inequalities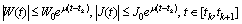

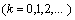where 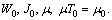are positive constants and 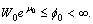Besides we point out that 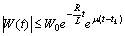implies the global estimate .

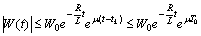Introduce the following family of pseudo-metrics

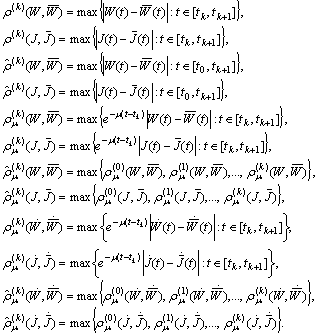The following inequalities imply the equivalence of the both families of pseudo-metrics

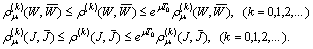It is easy to verify that

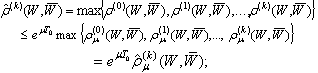(10)

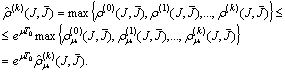The set 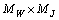turns out into a complete uniform space with respect to the family of pseudo-metrics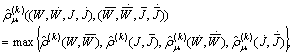

.

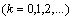Define the operator 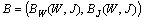by the formulas

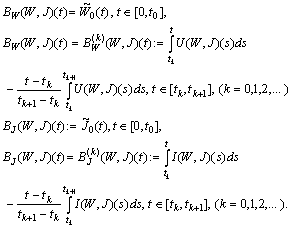The sources 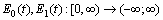are continuously differentiable oscillatory functions.

Further on the following assumptions will be hold:

Assumtion(IN):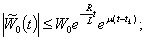

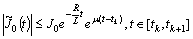Assumtion (E): ;

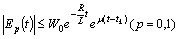Assumption (П): .

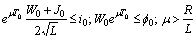Lemma 3.1. Problem (8) has a solution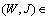 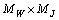iff the operator 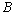has a fixed point in 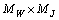, that is,

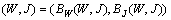(11)

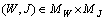Proof: Let be a solution of (8). Then integrating every equation of (8) on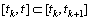 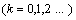we obtain

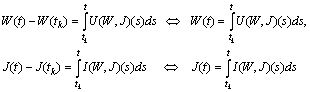and then

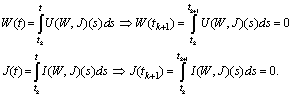(12)

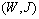Therefore the pair satisfies

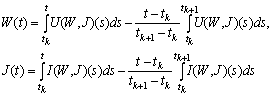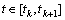for or 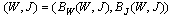, that is, 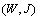is a fixed point of B.

Conversely, let 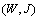be a fixed point of B or

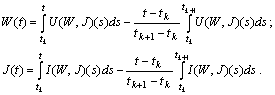(13)

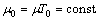Then in view of we obtain

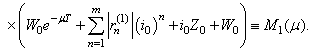Since 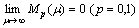we conclude that

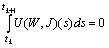and .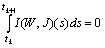

Therefore operator equations (13) become

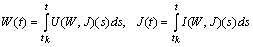Differentiating the last integral equations we obtain (8).

Lemma 3.1 is thus proved.

Preliminary assertions:

;

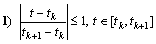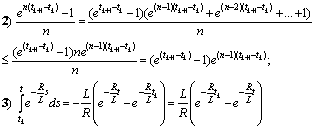
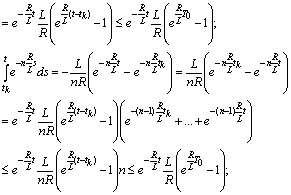
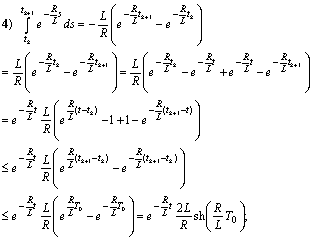
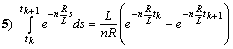
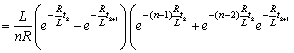
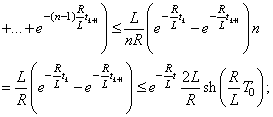6) the function 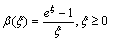is increasing and ;

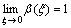Theorem 3.1. In addition to conditions (IN), (E) and (П) suppose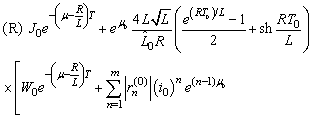

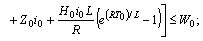
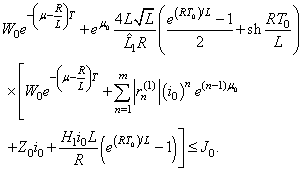Then there exists an unique oscillatory solution of (8), belonging to .

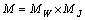Proof: Recall that 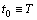we notice that the function 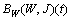is continuous on .

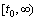Indeed,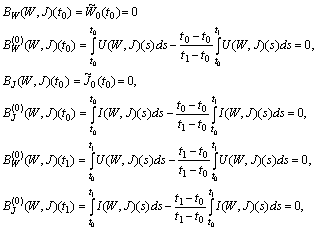

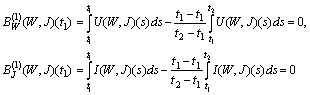and for :

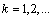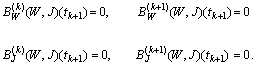We notice also 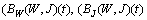are differentiable on every interval .

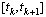In order to show that 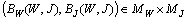we have to establish the following inequalities:

, .

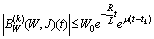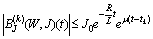Using Preliminary assertions we have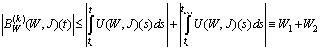

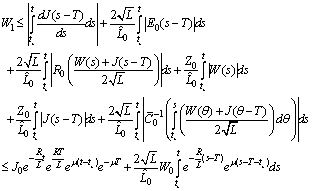
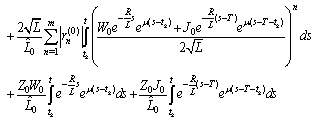
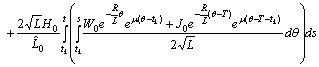
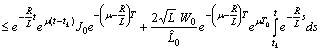
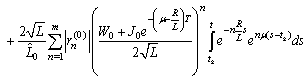
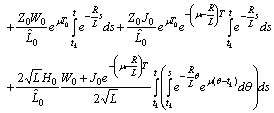
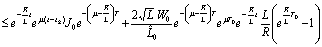
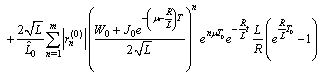
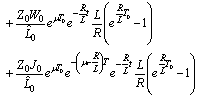
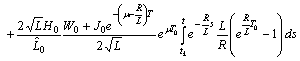
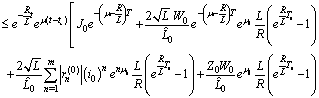
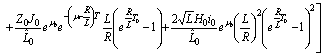
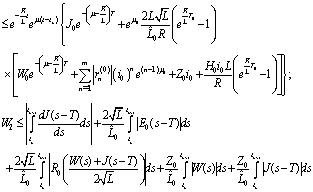
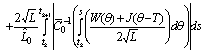
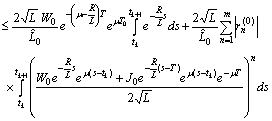
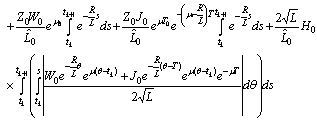
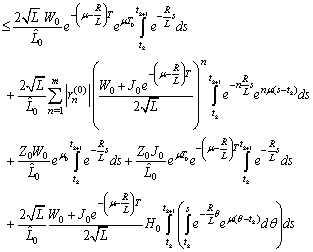
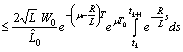
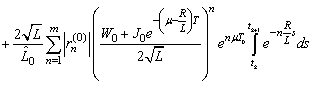
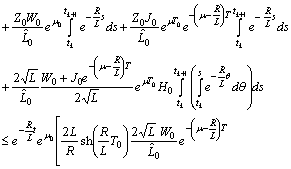
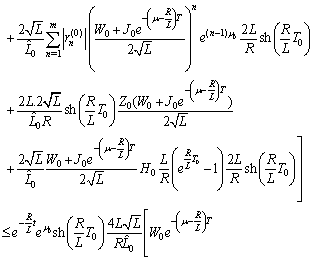
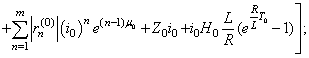
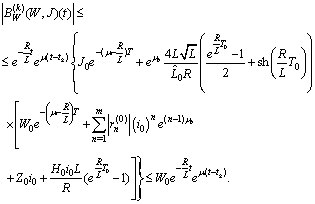For the second component we have

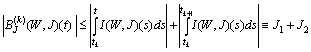and then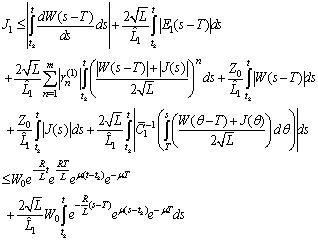

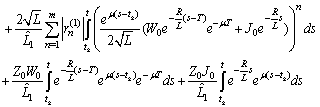
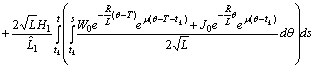
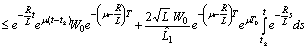
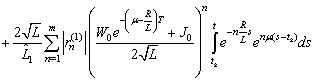
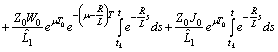
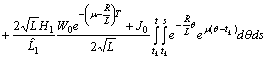
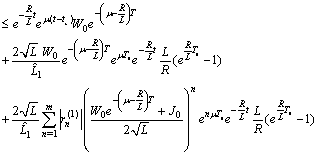
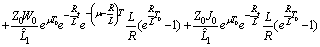
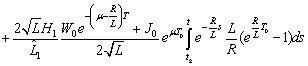
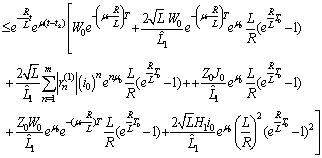
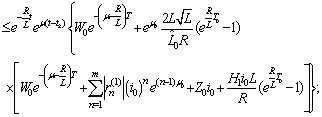
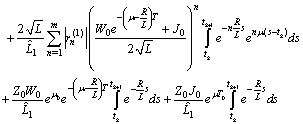
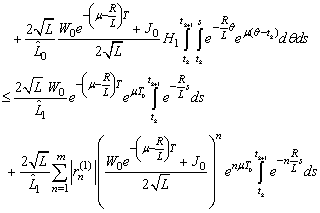
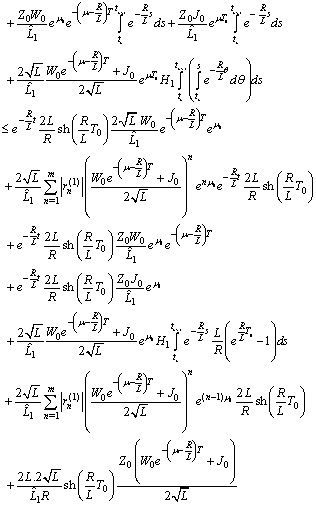
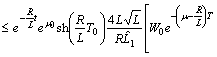
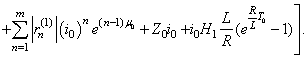Therefore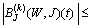

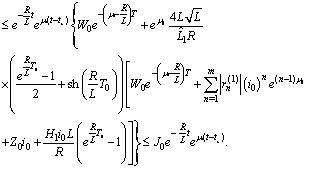So the operator B maps the set 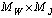into itself.

In what follows we show that B is contractive operator.

The maximum of

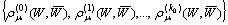attends for some 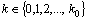. Then

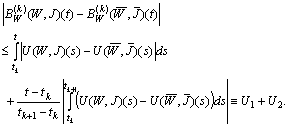We have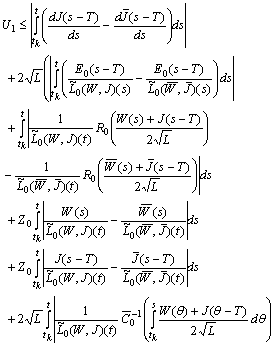

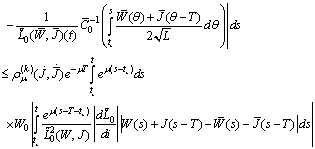
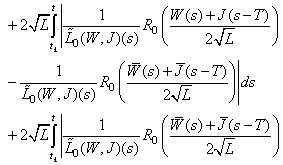
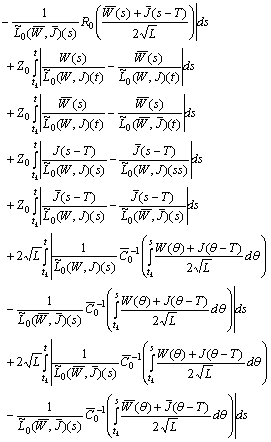
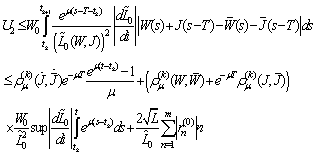
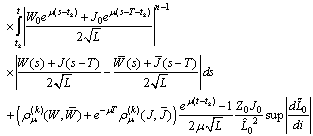
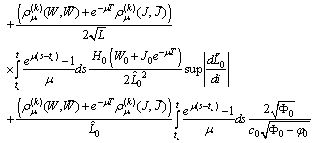
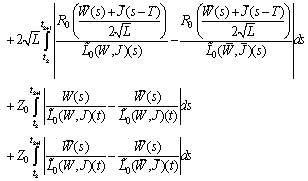
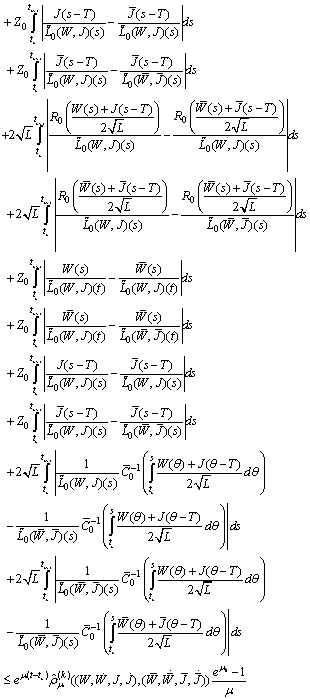
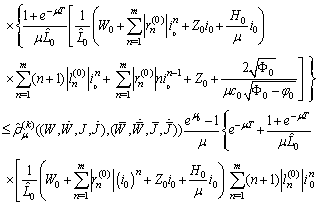
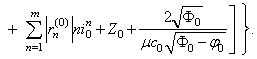Therefore

It follows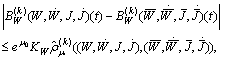

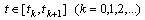and consequently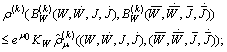

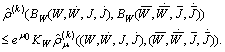Further on we have

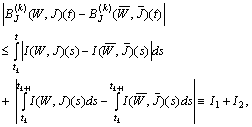We get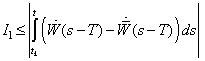

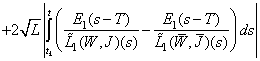
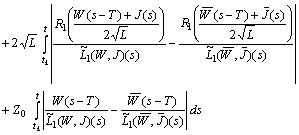
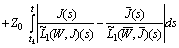
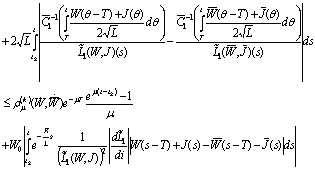
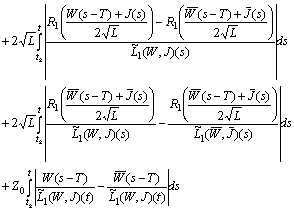
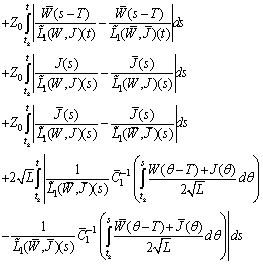
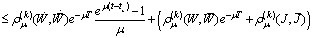
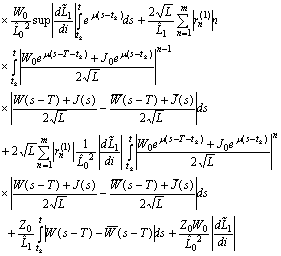
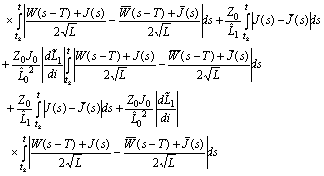
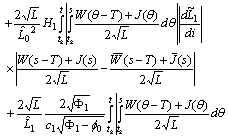
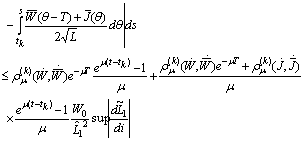
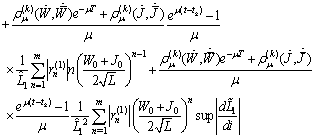
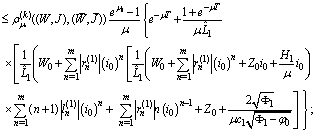
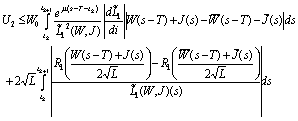
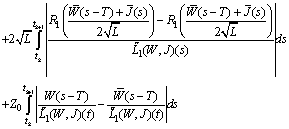
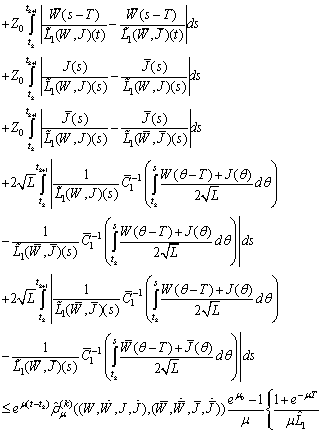
Therefore

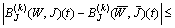
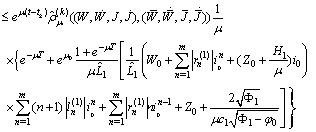
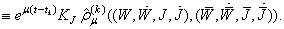It follows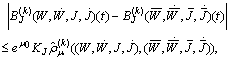

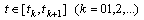and consequently

Finally we have to obtain an estimate of the derivatives for :

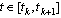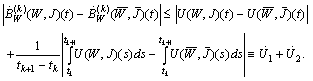We get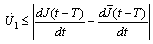

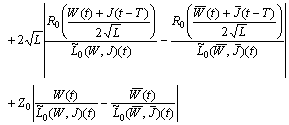
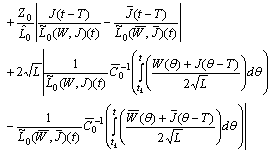
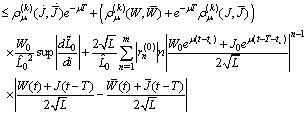
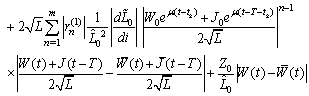
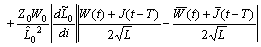
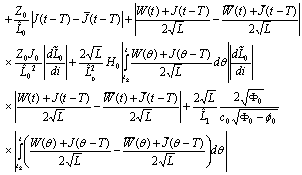
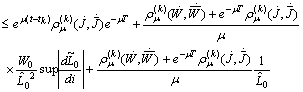
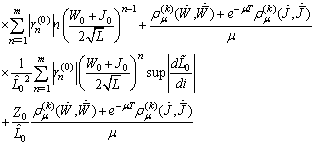
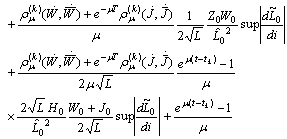
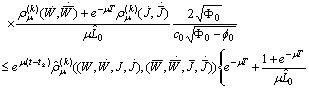
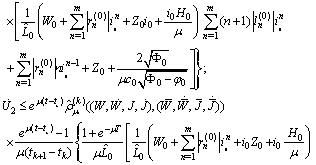
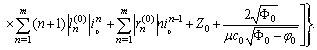The last term is bounded because

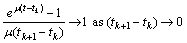and .

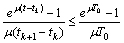Consequently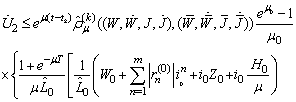

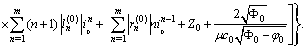Therefore

that is,

It follows

For the derivative of the second component of B we obtain

.

We have

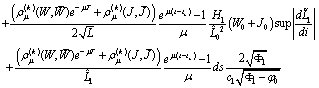
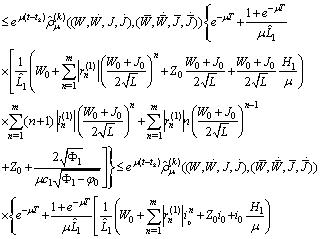
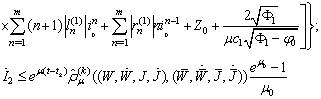
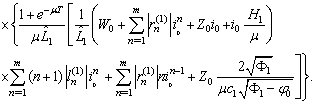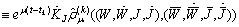Then

.

Then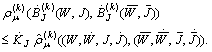

It follows

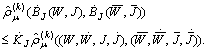Finally we obtain

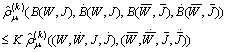where 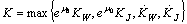might be chosen smaller than 1.

Therefore B is contractive operator and has a unique fixed point in M (cf.[3], Theorems 2.2.2 and 2.2.3). It is an oscillatory solution of (8).

Thus Theorem 3.1 is thus proved.

4. Numerical Example

Finally we demonstrate of how to apply the above theorem to engineering problems. We collect all inequalities implying an existence-uniqueness of oscillatory solution:

; ;

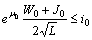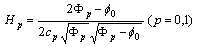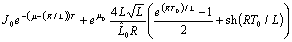
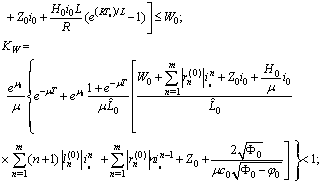
For a transmission line with length ; .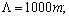

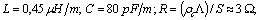
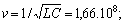
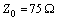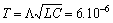For waves with 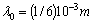we have

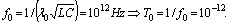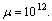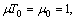Let us choose Then and 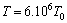. Consequently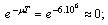

.

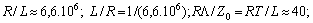
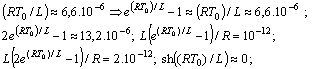
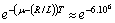We choose resistive elements with V-I characteristics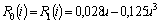

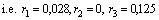and inductive element with .

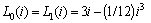Then 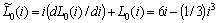and

.

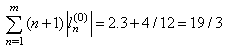For 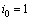one obtains

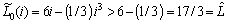and consequently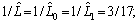

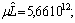
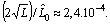Let us take

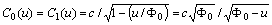, where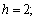

.

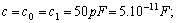
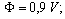
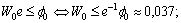
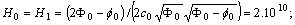
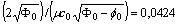We can take 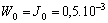. Then the above inequalities become

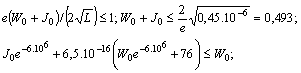Let the initial approximation be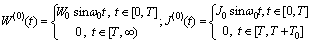

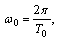
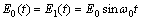and .

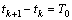Then we have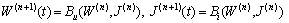

.

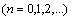Since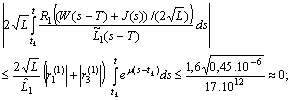

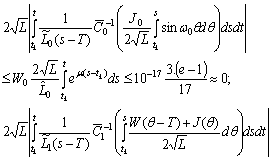
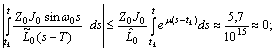
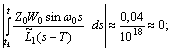then the first approximations become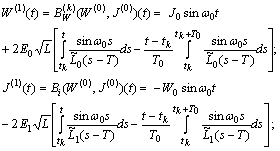

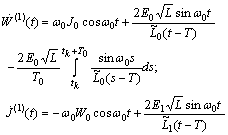
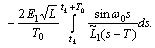Consequently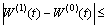

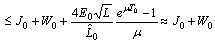and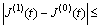

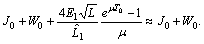For the derivative we have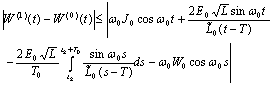

.

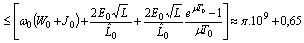In the same way we can obtain estimates for the second component of the operator B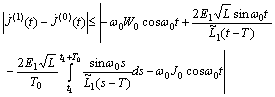

.

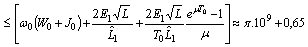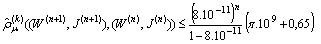
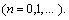
5. Conclusions

• We consider transmission lines taking into account the lossies. This means there is attenuation in time of the signals. This natural physical fact is confirmed by the mathematical method we apply. Namely, the transformation (we have used to reduce the mixed problem for hyperbolic system to a problem for neutral system on the boundary) contains an exponential function 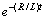which implies that signals (current and voltage) vanish exponentially. It reminds us that natural global solutions are not periodic ones. That is why we formulate the problem of existence-uniqueness of an oscillatory solution.

• In order to prove an existence-uniqueness theorem we introduce an operator (unknown in the literature up to now) whose fixed points are oscillatory solution of the problem stated.

• It turns out that the space of oscillating functions does not form a metric space but a uniform one. This requires applying fixed point theorems of operators acting on uniform spaces.

• We would like to point out that by means of this fixed point method we solve nonlinear equations with various nonlinearities as polynomial, exponential and transcendental ones.

• By virtue of the theorems obtained in this paper we show that attenuating oscillating modes are natural for the lossy transmission lines terminated by such configuration of the nonlinear loads.

• The numerical example demonstrates a frame of applicability of the theory exposed (for instance to design of circuits) and shows that the method could be applied checking few simple inequalities between the basic specific parameter of the lines and loads.

• Finally we note that a lot of papers have been done where numerical (or other) methods are applied without uniqueness is assured. Then it is not clear to which solution is approaching. Our fixed point method guarantees a uniqueness of solution.

• The calculation of the successive approximations and the estimations of some terms (leading to their disregarding) simplify the calculation of the next approximations. It is extremely important for any program implementing the method.