Reinoud Jan Slagter
Department of Physics, University of Amsterdam and ASFYON, Bussum, 1405EP, The Netherlands
Correspondence to: Reinoud Jan Slagter , Department of Physics, University of Amsterdam and ASFYON, Bussum, 1405EP, The Netherlands.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Cosmic strings can be formed in symmetry-breaking phase transition in the early stage of the universe. They are topological defects, analogous to flux tubes in type-II superconductors, or to vortex filaments in superfluid helium. Cosmic strings consist of trapped regions of false vacuum in U(1) gauge theories with spontaneous symmetry breaking. Density perturbations that would be produced by these strings of GUT scale, Gμ= η2/Mpl2 = 10-6, where G=1/Mpl2is Newton's constant, Mpl the Planck mass, μ the mass per unit length of the string and η the symmetry breaking scale, could have served as seeds for the formation of galaxies and clusters. However, recent observation of the cosmic microwave back-ground (CMB) radiation disfavored this scenario. The WAMP-data prove that cosmic strings can't contribute more than an insignificant proportion of the primordial density perturbation,Gμ ≤ 10-6. The space time around a cosmic string is conical, with an angle deficit ∆θ ~ μ. They should produce axially symmetric gravitational lensing effect, not found by observations. Recently, braneworld scenarios suggest the existence of fundamental strings, predicted by superstring theory. These super-massive cosmic strings, Gμ~1, could be produced when the universe underwent phase transitions at energies much higher than the GUT scale. To overcome the conflict with observational bounds, we present the classical Nielsen-Olesen string solution on a warped five dimensional space time, where we solved the effective four dimensional equations from the fivedimensional equations together with the junction and boundary conditions. Where the mass per unit length in the bulk can be of order of the Planck scale, in the brane it will be warped down to unobservable GUT scale. It turns out that the induced four dimensional space timedoes notshow asymptotic conical behaviour. So there is no angle deficit and the space time seems to be un-physical, at least under fairly weak assumptions on the stress-energy tensor and without a positive brane tension. The results are confirmed by numerical solutions of the field equations.
Keywords:
Cosmic Strings, Warped Space Times, BraneWorlds, Higher Dimensional Cosmology
1. Introduction
The standard model is extremely successful up to scales MEW ~103GeV. The fundamental scale of gravity is the Planck scale, MPl ~ 1019 GeV. It is the scale where quantum gravity will act. The discrepancy between these two scales is called the hierarchy problem. Electro-weak interactions have been tested up to MEW , while gravity, on the other hand, has been tested to several millimetres, 32 orders of magnitude above MPl.Braneworld models could overcome the hierarchy problem. The idea originates from string theory.One of the predictions of string theory is the existence of branes embedded in the full bulk space time. Gravitons can then propagate into the bulk, while other fields are confined to these branes. It also predicts that space time is 10-dimensional, with 6 of them are very compact and small, not verifiable by any experiment. There are many models which attacked the hierarchy problem. Essentially there are globally two categories: flat compact extra dimensions and warped extra dimensions.Recently, there is growing interest in the second category, i.e., the Randall-Sundrum(RS) warped 5-dimensional geometry ([1],[2]). We live in a 3+1 dimensional space time embedded in a 5-dimensional space time, with an extra dimension which can be very large compared to the ones predicted in string theory. One estimates that the extra dimension can be as large as 10-3 cm, which is the under-bound of Newton's law in our world.The observed 4-dimensional Planck scale Mpl = M4is no longer the fundamental scale but an effective one, an important consequence of the extra dimensions, which is now M5, the Planck scale in 5D. The weakness of gravity can be understand by the fact that it "spreads" into the extra dimension and only a part is felt in the 4-dimensional brane.Spontaneously broken gauge theories give rise to topological defects, such as cosmic strings, monopoles and domain walls. The simplest model is a U(1) gauge theory, involving a complex scalar field Φ interacting with the electromagnetic gauge field and a "sombrero"-potential V(Φ) and described by the Lagrangian density ([3])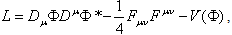 | (1) |
withFμν the electromagnetic tensor and Dμ the gauge-covariant derivative. Cosmic strings occur as topological defects, consisting of confined regions of false vacuum in gauge theories with spontaneous symmetry breaking. When the temperature in the early universe falls down,the scalar field will develop a locus of trapped points of valse vacuum. This formation of vortices is equivalent to the Ginzburg-Landau theory of type II superconductivity.If local strings appeared in phase transitions in the early universe,they could have served as seeds for the formation of galaxies. However, observations of the cosmic microwave background, would rule out this model. Cosmic strings possess a conicalspace time, with an angle deficit which could produce axially symmetric gravitational lens effects, not found by observations ([4]).M-theory, the improved version of superstring theory, allows, via braneworld scenarios, macroscopic fundamental strings that could play a role very similar to that of cosmic strings ([5],[6],[7])The resulting super-massive cosmic strings are even more exotic, because they could develop singular behaviour at finite distance of the core of the string ([8],[9]).We will investigate on an axially symmetric 5-dimensional warped space time the modifications of the behaviour of a gauge cosmic string in the Abelian Higgs model. The general relativistic cosmic string was first investigated by Garfinkle ([10]) and later extended by Dyer and Marleau ([11]).In section 2 we outline the revised U(1) cosmic string in 5D and present some numerical solutions. In section 3 we de investigate the angle deficit and the changes with respect to the 4D model.
2. The Model
Let us consider the warped 5 dimensional space time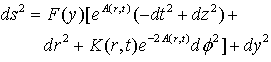 | (2) |
F(y) the warp factor and y the extra dimension. For F=1 and y=0 we recognize the 4D axially symmetric space time. We will follow the notations of references[12]-[15].If there is a bulk scalar field (5)Φ (no coupling to a 5D gauge field Aμ , as in the 4D case), which could stabilize the branes ([16]), then we have for the 5D equations (from now on all the indices run from 0..4)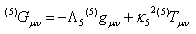 | (3) |
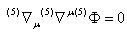 | (4) |
with(5)Tμυ the energy momentum tensor of the bulk scalar field. When we write (5)Φ=(5)Xeiφ, then it turns out that the y-dependent part is separable. We obtain for F(y) and (5)X(y) the set equations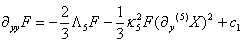 | (5) |
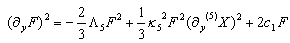 | (6) |
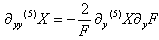 | (7) |
with c1 some constant. For c1=0 there exist exact solutions for F(y) and (5)X(y). It is remarkable that these equations for F(y) and (5)X(y) are separable.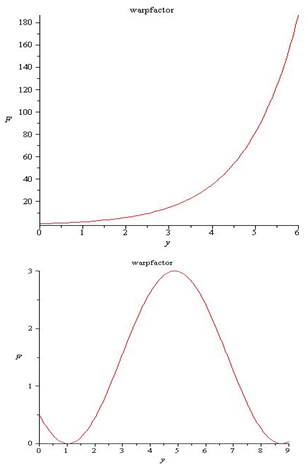 | Figure 1. The warpfactor F(y) in the case of an empty bulk for positive bulk cosmological constant (upper) and negative one |
From now on we will consider the case of an empty bulk (c1 ≠1) and the field equations on the brane time-independent. There are two solutions for F, plotted in figure 1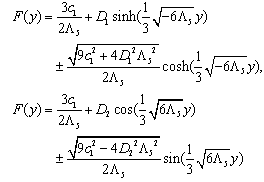 | (8) |
with Di some constants.From the Einstein equations one obtains a constraint equation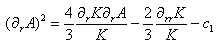 | (9) |
Constraint systems appear whenever a theory has gauge symmetry, in general relativity equivalent to coordinate change. Gauge invariance implies here general covariance under coordinate transformations. In terms of fields on a space time one says that the theory has redundancy and the constraint equations are preserved in time ([17]).Let us now investigate the induced field equations on the brane. Following[14] we obtain | Figure 2.The 5-dimensional cosmic string |
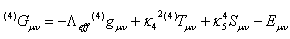 | (10) |
whereΛeff=½(Λ5+κ42λ4) and λ4 the vacuum energy in the brane ( brane tension). (4)Tμν is the 4 dimensional energy momentum tensor. The equations for the 4D scalar and gauge fields are the same as in the 4D case([10]). The first correction term Sμν is the quadratic term in the energy-momentum tensor arising from the extrinsic curvature terms in the projected Einstein tensor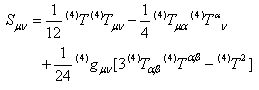 | (11) |
The second correction term Eμν is given by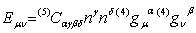 | (12) |
and is a part of the 5D Weyl tensor and carries information of the gravitational field outside the brane and is constrained by the motion of the matter on the brane, i.e., the Codazzi equation.The induced metric on the brane is given by (4)gμν= (5)gμν- nμnν , with nμ the unit normal vector on the brane. Eμνrepresents the 5D graviton effects, i.e., Kaluza-Klein modes in the linearized theory ([1],[2]). In the static case of the space time (2), one can evaluate the equations for K and A and the gauge fields X and P. In order to compare the change in behaviour of these equations with respect to 4D counterpart equations, we take the same combinations of the components of the Einstein equations as in the 4D case. The result is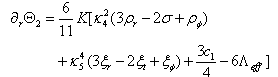 | (13) |
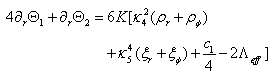 | (14) |
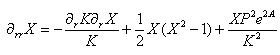 | (15) |
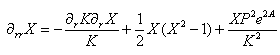 | (16) |
where we used the same notations as in the 4D case , i.e., Θ1=K∂rA and Θ2=∂rK. Further, we write the energy momentum tensors as Tμν=σktkt+ρzkzkz+ρφkφkφ+ρrkrkr, Sμν=ξtktkt+ξzkzkz+ξφkφkφ+ξrkrkr, with ki a set of orthonormal vectors on the 4D space time. We also used the constraint equation of (9). In the 4D case, the equations are, ∂rΘ1=κ42K(ρr+ρφ) and ∂rΘ2=½κ42K(3ρr-2σ+ρφ), so we recognize the κ4-terms in ( 13) and (14). In the special case of c1 = 8Λeff , we see on the right hand side that the κ5 term has the same combinations of the components of the energy-momentum tensor Sμν. On the left hand side we observe a difference due to the consequence of the Eμν term entering the equations. We will use these equations to evaluate the angle deficit in our model. If we would take κ42 = λ4κ54/6 ([1]) we then have 5 parameters for the model, i.e., β, e, η, λ4 and κ5. The effective field equations are supplemented by the 5D equations and the conservationof stress-energy. We can compare the numerical solution of the 4D-brane equations with the "classical" Nielsen-Olesen solution. In figure 3 we plotted two solutions with the same initial conditions and parameters used by Garfinkle([10]). We used a standard routine using solely initial conditions. In order to find an "acceptable" solution, one has to fine tune the initial values ([11]). We observe that e-A K behaves differently. In the 4D case there is only a small deviation from Minkowski for large r, representing an angle deficit.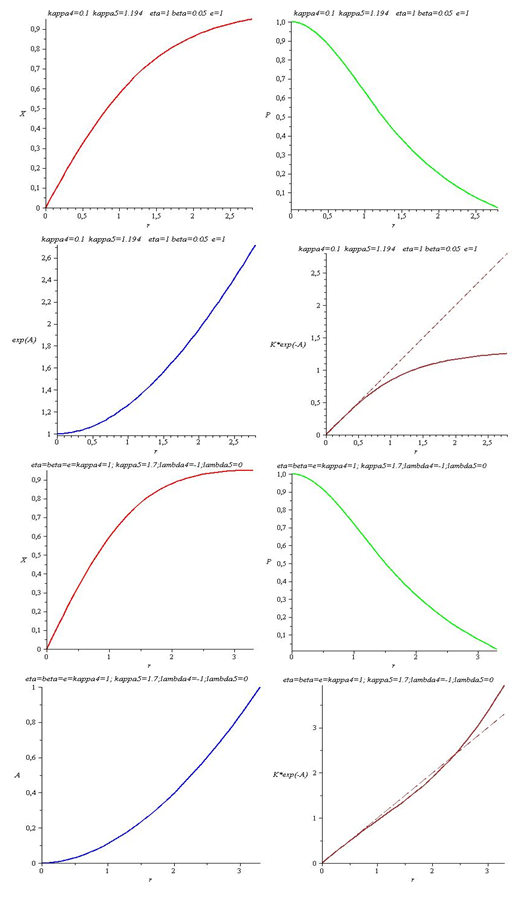 | Figure 3. Two characteristic solutions of the braneinduces U(1) gauge string. We used a standard "shooting" routine. We observe the same behaviour of X and P, but a significant different behaviour of e-AK. The dashed line represents the Minkowski space time |
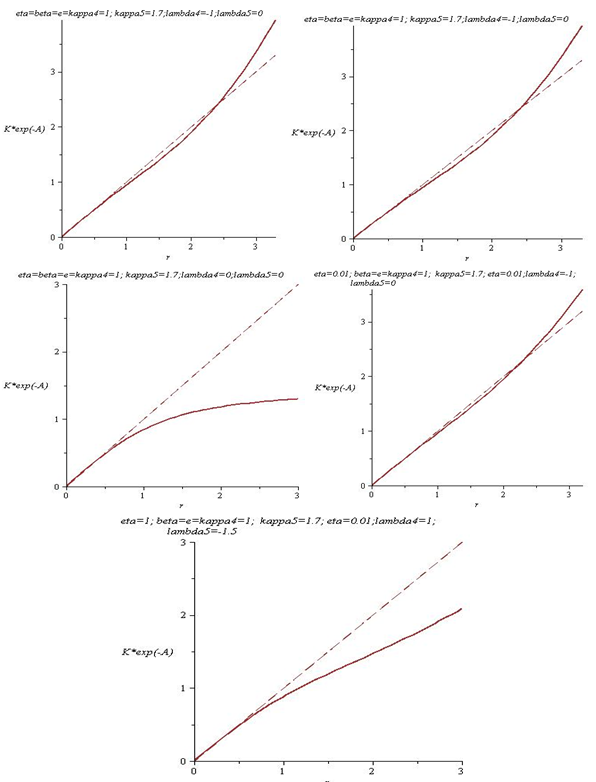 | Figure 4. Numerical solution of the metric component e-AKfor different values of the brane and bulk cosmological constants. The last one represents the most realistic situation, where λ4>0 and Λ5<0. The behaviour don't change significantly with increasing η |
In figure 4 we plotted e-AK for different values of the parameters. We don’t find a typical cosmic string behaviour as in the 4D case.For negative bulk cosmological constant, it seems to be possible to find a behaviour of e-AK which is comparable with the classical 4D behaviour ([10]). However, this is not a typical cosmic string situation.
3.Analysis of The Angle Deficit
The angle deficit can be calculated for a class of static translational symmetric space times which are asymptotically Minkowski minus a wedge. If we denote with l the length of an orbit of (∂/∂φ)a in the brane, then the angle deficitis given by[10]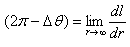 | (17) |
with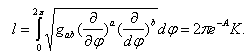 | (18) |
Using boundary conditions at the axis, we obtain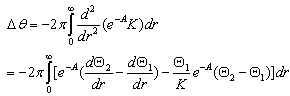 | (19) |
In order to evaluate the right hand side, we first calculate, as in the 4D case, the total derivative of the expression (κ42K2ρr) using the conservation of stress energy, 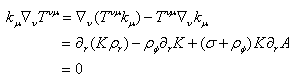 | (20) |
and the two field equations for A and K. We find after a straightforward calculation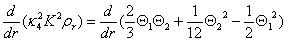 | (21) |
Using the case where c1 =8Λeff and boundary conditions at the axis, we obtain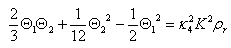 | (22) |
Further, we used that Sμν ~ (Tμν)2, so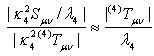 | (23) |
Further we assumed |(4)Tμν | << λ4 ([14]). As in the 4D case we have also 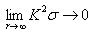 and σ > |ρr| > |ρφ|. From the field equations we then have that Θ1 and Θ2 approach constant values k1 and k2 as r→∞. The solution of (22)then yields
and σ > |ρr| > |ρφ|. From the field equations we then have that Θ1 and Θ2 approach constant values k1 and k2 as r→∞. The solution of (22)then yields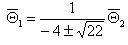 | (24) |
where we denote with 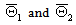 the asymptotic values.So we have for
the asymptotic values.So we have for 
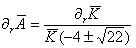 | (25) |
The solutions for 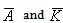 are then
are then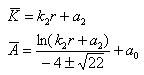 | (26) |
with a0 and a2 some constants. The space time becomes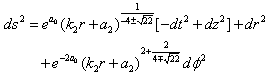 | (27) |
Let us compare our relation (22) with the 4D result: Θ1(Θ2-3/4Θ1)=κ42K2ρr. The solutionresults in a conical space time ([10]). In our case this solution is no option. We have now two possibilities for the asymptotic space time: both non-Kasner-like and non-conical. Combined with the warp factor F(y), the space time becomes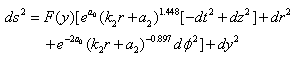 | (28) |
or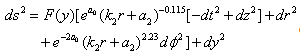 | (29) |
with F(y) in the empty bulk situation given by (8). These solutions are in general un-physical. The behaviour depends on the sign of k2/a2. Under less restrictive conditions, for example, c1 ≠ 8Λeffand with special choices of the parameters, the numerical solutions show some regular behaviour.Now we can evaluate the angle deficit. We can make a linear combination of (13),(14) and (22) in order to isolate the term e-AKσ ( as in the 4D case). We obtain: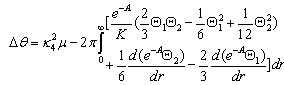 | (30) |
The first term is again the linear energy density of the string and is of order η2. The correction terms are in contrast with the 4D case, unbounded and will give chaotic results, as is seen in the numerical solutions of figure 4. Only for positive brane tension and negative bulk tension (the 5D braneworld preferred values) there seems to be a stable solution for e-A K. However, this solution cannot be classified as a cosmic string.
4. Conclusions
Cosmic strings produced in the Einstein-Higgs-gauge field model at GUT-scales give rise to a conical space time and could have important cosmological effects. Strings produced at much higher energy scales, i.e., Gμ>> 10-6 ,show singular behaviour. They seem to be inconsistent with the observed CMB spectrum. One believes that cosmic super-strings with energy scale close to the Planck scale arising at the end of brane inflation in braneworld cosmological models, could have comparable properties with respect to the GUT cosmic strings. Warped braneworld models with large extra dimensions could overcome the conflict with observation bounds. Here we considered on a warped 5D space time the "classical" self-gravitating Nielsen-Olesen vortex. It seems possible that the absence of evidence of cosmic strings in observational data could be explained by our model, where the conical feature disappears. In the super-massive case of Laguna and Garfinkle ([9]), i.e., where the linear mass per unit length Gμ>> 10-6, a continuous transition occurs from a conical space time to a Kasner-type with a curvature singularity at finite distance of the core for increasing symmetry breaking energy scale. In our induced brane space time we find a different result. On the brane, there is no conical space time, measured far from the core of the string. The solutions don't change significantly for increasing symmetry breaking scale η. We find an exact expression for the warp factor, which will warp down the found Kasner-like solutions. The numerical solutions confirm our conclusion.
References
| [1] | L. Randall, R. Sundrum, Phys. Rev. Lett. 83, 3370 , 1999. |
| [2] | L. Randall,R. Sundrum, Phys. Rev. Lett. 83, 4690, 1999. |
| [3] | H. B. Nielsen, P. Olesen, Nucl. Phys. B 61, 45, 1973 |
| [4] | A. Vilenkin, E. P. S. Shellard, Cosmic Strings and Other Topological Defects, Cambridge Monographs, Cambridge, 1994 |
| [5] | A. Vilenkin, arXiv: hep-th/0508135 |
| [6] | A. C. Davis, T. W. B. Kibble, arXiv: hep-th/0505050 |
| [7] | R. Gregory, arXiv: hep-th/9911015 |
| [8] | P. Laguna-Castillo, R. A. Matzner, Phys. Rev. D 36,3663, 1987 |
| [9] | P. Laguna, D. Garfinkle,Phys. Rev. D 40, 1011, 1989 |
| [10] | D. Garfinkle, Phys. Rev. D 32, 1323, 1985 |
| [11] | C. Dyer, F. Marleau,Phys. Rev. D 52, 5588, 1995 |
| [12] | N. Arkani-Hamed, S. Dimopoulos ,G. R. Dvali, Phys. Lett. B 429, 26, 1998 |
| [13] | T. Shiromizu, K. Maeda. M. Sasaki, arXiv: gr-qc/9910076 |
| [14] | R. Maartens, arXiv: gr-qc/0312059 |
| [15] | K. Aoyanagi, K. Maeda, arXiv: hep-th/0602149 |
| [16] | W. D. Goldberger, M. B. Wise, arXiv: hep-ph/9907447 |
| [17] | M. Bojowald,Canonical Gravity and Applications, Cambridge University press, Cambridge, 2011 |

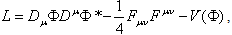
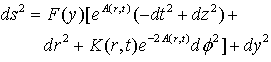
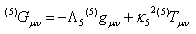
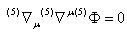
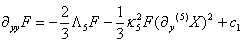
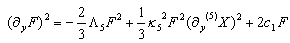
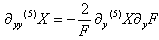

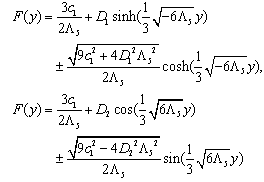
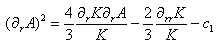

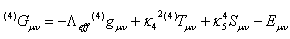
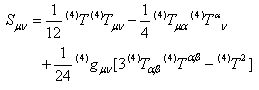
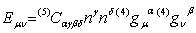
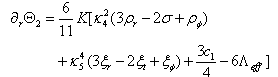
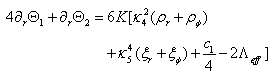
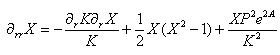
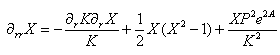
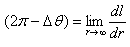
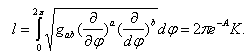
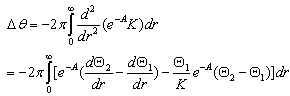
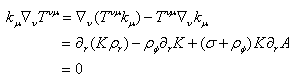
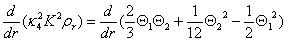
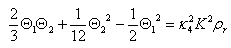
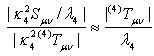
 and σ > |ρr| > |ρφ|. From the field equations we then have that Θ1 and Θ2 approach constant values k1 and k2 as r→∞. The solution of (22)then yields
and σ > |ρr| > |ρφ|. From the field equations we then have that Θ1 and Θ2 approach constant values k1 and k2 as r→∞. The solution of (22)then yields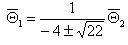
 the asymptotic values.So we have for
the asymptotic values.So we have for 
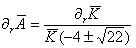
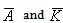 are then
are then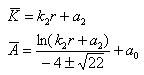
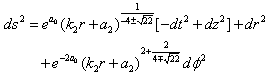
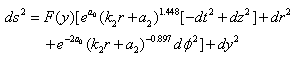
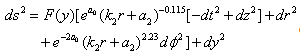
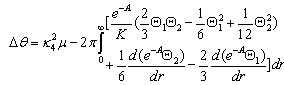
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML
