M. M. Abdelrahman , A. G. Helal , O. A. Moustafa , F. W. Abdelsalam
Accelerators&Ion Sources Department, Nuclear Research Center, Egyptian Atomic Energy Authority, Egypt
Correspondence to: M. M. Abdelrahman , Accelerators&Ion Sources Department, Nuclear Research Center, Egyptian Atomic Energy Authority, Egypt.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This work deals with the simulation process for the triode extraction system using SIMION computer program with and without space charge. Plasma boundary positions in ion extraction systems for different values of the extraction voltage at constant plasma density have been simulated and discussed. The motion of ion beam trajectories with and without space charge effect has been studied.
Keywords:
SIMION Program, Plasma Meniscus, Space Charge, Extraction Voltage
1. Introduction
Computer simulation codes provide a powerful tool for the optimization of charged particle systems[1]. However, the right program has to be selected to take full advantage of the computer. There are three classes of computer programs for the simulation of charged particle beams: (1) Envelope models, where the beam is described by ellipses in different projections of phase space. These ellipses are transformed by a matrix (transfer matrix), for each optical element of the beam line. This kind of programs can be used to analyze and optimize static beam transport sections (drift, electrostatic lenses, solenoids, and quadrupoles or sector magnets). (2) The particle tracking programs; which is more advanced than envelope models, where can be used to transfer matrices by tracking single particles instead of three ellipse parameters. (3) The ray tracing programs where this kind of programs can be used to simulate the charged particle beam within the extraction system. One of these ray tracing programs is SIMOION program. SIMION 3D 7.0 is a full windows program[2], featuring 3D electrostatic/magnetic arrays, data recording, charge repulsion, solid geometry definition files and a user program interface. The original version of the SIMION program for an electrostatic lens has been developed by D.C. McGilvery at Latrobe University in Australia (1977)[3]. SIMION provides direct and highly interactive methods for simulating a wide variety of general ion optics problems, as designing and analyzing charged particle (ions and electrons) lenses, ion transport systems, various types of mass spectrometers, detector optics, time of flight instruments, ion traps, quadrupoles, magnetic sectors, etc. Ion trajectories can be simulated, flying ions singly or in groups through the created geometry displayed as lines and automatically re-flown.The second important step for plasma ion sources after the production of suitable plasma is to extract the plasma ions in the form of an ion beam with given kinetic energy. This can be done by using an electrode system that is biased at a negative voltage with respect to the plasma. The value of the extracted ion current should be large, its divergence low and the ion losses to the extractor electrode must be small. Ion beam quality is affected by many factors as the applied extraction voltage and the shape of the emitting plasma surface which may be fixed (field and surface ionization sources) or variable (plasma sources), and on the space charge in the ion beam. In the case of plasma sources, the shape of the plasma surface is not fixed by any mechanical means but is determined by the rate of the influx of the ions from the plasma surface and the rate of their withdrawal by the potential of the extractor.
1.1. Influence of the Shape of the Plasma Boundary
The plasma is practically an equipotential and electrically neutral medium. When it comes in contact with an electrode held at a different potential, a plasma sheath is formed and almost the whole potential difference between the plasma and the electrode develops along this sheath. The position and the shape of the plasma boundary are affected by the ion density, the extraction voltage and the geometry of the extraction system. The value of the ion density inside the ion source is governed by the discharge parameters as magnetic field, gas pressure, and RF power in the case of RF ion sources. As the potential between the plasma and the electrode may change, the thickness of the sheath varies accordingly. When this potential difference is gradually increased, the plasma boundary retreats until it becomes flat and finally concave at an appropriately high value of the extraction potential. The variation of the plasma sheath with respect to the change in extraction potential at constant plasma density is illustrated in fig.1. When there is no applied voltage at the extractor, the plasma will extend throughout the discharge region and also through the aperture of the plasma electrode (Fig.1a). With a low negative voltage applied to the extractor electrode, the plasma boundary will retreat toward the discharge chamber. In this case, the extracted ions will strongly diverge, because of the convex shape of the plasma boundary (Fig.1.b, c). By applying appropriately higher values of the extraction potential to the extractor, the plasma boundary will move further back into the discharge chamber according to the applied voltage which just defines space charge limited ion flow from the plasma boundary according to that which the plasma can furnish (Fig.1d).When the plasma density in front of the extraction hole is varied, the maximum achievable current density ji under space charge limited conditions follows from the Child-Langmuir law: ji is given by (assumption of idealized plane plasma geometry)[4: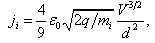 | (1) |
where V is the acceleration voltage for the ion beam, mi is the ion mass and ε0 is the permittivity of free space, d is the characteristic extraction gap width and q = ze, with z the ion charge state and e is the electron charge. According to Bohm’s law5, a plasma with certain parameters (plasma density, electron temperature) can provide a specific ion current density. The assumed extraction geometry and potential distribution together with an assumed plasma meniscus shape and position permits a certain space charge limited ion current density according to equ.1. This space charge limited ion current density will correspond with the Bohm current density since the plasma meniscus will adapt itself accordingly. The ion current density ji extractable from a plasma boundary is given by the formula of Bohm: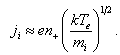 | (2) |
The ions must reach the plasma sheath with a kinetic energy corresponding to the plasma electron temperature 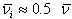 where
where 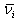 is the mean velocity of the ions after crossing the plasma sheath. The mean velocity
is the mean velocity of the ions after crossing the plasma sheath. The mean velocity 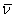 is given by:
is given by: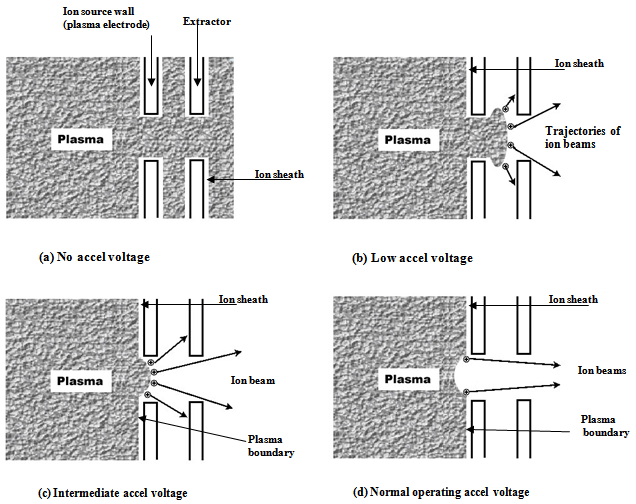 | Figure 1. Plasma boundary positions in an ion extraction system for different values of the extraction voltage |
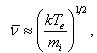 | (3) |
where k is the Boltzmann constant, Te is the electron temperature and n+ is the ion density at the plasma boundary.The quality of an ion beam can be defined by, e.g., its perveance P: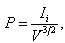 | (4) |
where Ii is the total ion beam current and V is the acceleration voltage of the ion beam.
1.2. Ion Beam Trajectories without and with Space Charge
Ion beams which propagate through a given beamline construction suffer from a beam *blow up*, which refers to the tendency for like–charged (positive) ions within the ion beam to mutually repel each other (space–charge effect) and the increase of the emittance (Fig. 2). Beam–blow up is a practical problem in high current ion sources, and in order to reduce this problem, space charge neutralization has to be used. This mechanism is the creation of beam plasma which consists of positively charged, negatively charged and neutral particles (Fig. 3). Beam plasma is created when the positively charged ion beam interacts with residual background gas atoms in its path, producing ion–electron pairs[6. The influence of ion space charge is disadvantageous to both the quality and quantity of the extracted ion beam[7. In beam–plasma ion sources, the ion beam is extracted with the ion space charge neutralized by electrons. The electrons used for ion space charge compensation can be divided into three groups: the primary electron beam which injected from the cathode electrode into the drift tube (plasma chamber), the secondary electron beam and the plasma electrons. The space charge of the primary electron beam is distributed within the whole extraction region. Secondary electron beam are produced in the collector region due to the bombardment of the primary electron beam on the collector electrode. The space charge of the secondary electron beam is distributed at the ion – extraction position with a potential corresponding to the energy of the beam.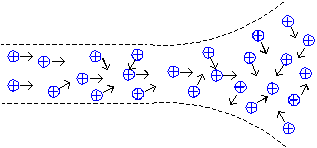 | Figure 2. Beam blow up, space charge effect |
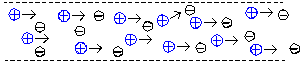 | Figure 3. Space charge compensation of positive beam ions |
For ion sources, some of the residual gas particles that are present in the beam line will be ionized by ion impact and thus a sufficient number of compensating electrons is generated which must be kept from being accelerated back into the source by the extraction field.The electron density plays an important role in the compensation of the ion space charge. Therefore, space charge of the ion beam is compensated as[8: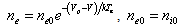 | (5) |
where ne and ni are the electron and ion densities, respectively, which are equal in the beam plasma, kTe refers to the electron temperature, Vp is the plasma potential and V is the acceleration voltage of the ion beams.In the presence of space charge, the electric field acting on a cylindrically symmetric ion beam is[9]: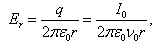 | (6) |
where 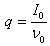 is the charge of the beam per unit length within the beam radius r, I0 is the total beam current, and
is the charge of the beam per unit length within the beam radius r, I0 is the total beam current, and 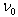 the axial ion velocity.For higher ion currents at a low acceleration voltage, the ion space charge in the extraction region is high and then the beam will diverge within a short distance if space charge is not fully compensated. When the space charge of the ion beam is compensated by electrons, no radial force affects the ion beam.
the axial ion velocity.For higher ion currents at a low acceleration voltage, the ion space charge in the extraction region is high and then the beam will diverge within a short distance if space charge is not fully compensated. When the space charge of the ion beam is compensated by electrons, no radial force affects the ion beam.
2. Simulation of the Ion Beam Trajectories for Variable Plasma Meniscus
Simulation of the singly charged argon ion trajectories for a variable meniscus shape of the plasma was studied using SIMION computer program with and without space charge. Design of the triode extraction system has been done with the same dimensions by using SIMION computer program. For a fixed geometry of the triode extraction system, singly charged argon ion trajectories for variable plasma meniscus under the influence of the acceleration voltage have been investigated with and without space charge.Beam emittance as a function of the extraction gap for a concave shape at acceleration voltage Vacc = - 2000 V has been studied without space charge effect as an example where at this voltage, the ion beam envelope was best passed through the extraction region . Also, beam emittance as a function of the curvature of the variable plasma meniscus at acceleration voltages Vacc = - 2000 V has been investigated.
2.1. Design of the Triode Extraction System
In order to extract ion beams from the appropriate ion source, an arrangement of carefully designed must be used. This electrode must create the proper configuration of the electric field at the surface of the ion source and along the acceleration of the ion beam region. The surface which forms the source of ions can be either of fixed geometry (surface ionization and field ion sources)[10 or it can be the boundary of the plasma (plasma ion sources)[11 in which the shape of the surface is fluid depending on the current density, ion supply rate and the electric field applied. The design of an extraction system must take into account the nature of this system and must initiate the ion beam as free of aberrations as possible. The triode extraction system features a 5 mm diameter plasma aperture, an accel–and a decel–electrode. For ion sources, some of the residual gas particles that are present within the beam line will be ionized by hitting the ions and thus a sufficient number of compensating electrons is generated which must be kept from being accelerated back into the source by the extraction field. This triode extraction system operated in accel–decel mode provides a negative voltage on the axis of the extraction system. This negative voltage creates a well for electrons to keep them inside the beam. 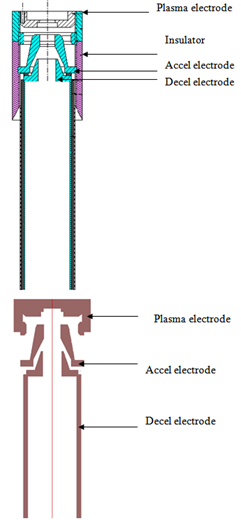 | Figure 4a, b. (a) Triode extraction system mechanically designed. (b) Triode extraction system designed with the same dimensions using SIMION Program |
The electrons provide the space charge compensation. The triode extraction system consists of three electrodes. The first electrode is called plasma electrode. In this study, this electrode is set to a voltage of + 5 kV and this plasma electrode was considered as the plasma emission surface, where the ions are starting to fly. The plasma electrode terminates the plasma surface at one end of the discharge. The downstream side of this electrode must be designed to affect as a focus electrode to provide the proper electric field configuration which will give optimum ion trajectories. For this reason, a design of the plasma electrode in which the upstream side is tapered. The second electrode is called accel electrode and a voltage applied on it in this study varied between (–5 to + 5 kV). The third electrode of the triode extraction system is called decel electrode and is set to a voltage of 0 V. Triode extraction system designed mechanically and designed with the same dimensions using SIMION program are shown in Fig.4 a, b.
3. Calculations of the Extraction System for Variable Plasma Meniscus with and without Space Charge
Using SIMION computer program, simulation of the singly charged argon ion trajectories for a variable plasma meniscus was studied with and without space charge[12. Beam emittance as a function of the extraction gap for a concave shape at acceleration voltage Vacc = - 2000 V on the accel electrode has been studied for singly charged argon ion trajectories. Also, at acceleration voltage Vacc = - 2000 V, beam emittance as a function of the curvature of the plasma meniscus for different shapes has been investigated In the most of the concave and convex shapes, beam emittance has been calculated by using separate standard deviations of positions and elevations angles. In the present study, beam emittance was calculated by using the separate standard deviations of the positions (σy) and the elevation angles (σα) for singly charged argon ion trajectories;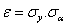 | (7) |
Standard deviation can be defined for positions as;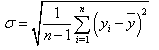 | (8) |
where 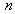 is the number of repeated measurements,
is the number of repeated measurements, 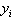 is the individual
is the individual 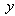 -values and
-values and 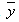 is the mean value of the repeated
is the mean value of the repeated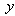 -values. For a fixed geometry of the triode extraction system, the following calculations have been done with and without space charge:
-values. For a fixed geometry of the triode extraction system, the following calculations have been done with and without space charge:
3.1. Without Space Charge
3.1.1. Flat Shape
The influence of the acceleration voltage applied to the acceleration electrode of the triode extraction system on ion beam emittance for flat plasma shape has been investigated as shown in Fig.5. It is clear that the ion beam emittance increases with increasing the negative voltage applied to the acceleration electrode. While applying positive voltage to the acceleration electrode is accompanied by a decrease of the extracted ion beam emittance.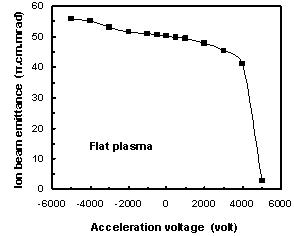 | Figure 5. Influence of the acceleration voltage on ion beam emittance for flat plasma shape without space charge |
3.1.2. Concave Shapes
The curvature of the plasma concave shapes of 2.5, 2.7, 3.5, 3.75, 4 and 8.15 mm have been obtained. The influence of the acceleration voltage applied to the acceleration electrode of the triode extraction system on the extracted ion beam emittance for various curvatures of the concave plasma shapes have been investigated as shown in Fig. 6. It is clear that the minimum ion beam emittance has been obtained for a plasma curvature of 3.75 mm. In the most of the concave shape cases, the extracted ion beam emittance increases with increasing the negative voltage applied to the acceleration electrode. While applying positive voltage to acceleration electrode is accompanied by a decrease of the extracted ion beam emittance.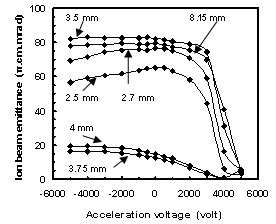 | Figure 6. Influence of the acceleration voltage on ion beam emittance for various curvatures of the concave plasma shapes without space charge without space charge |
3.1.3. Convex Shapes
The curvatures of the plasma convex shapes of 2.5, 2.7, 3.5, 3.75, 4 and 8.15 mm have been obtained. Also, the influence of the acceleration voltage applied to the acceleration electrode of the triode extraction system on ion beam emittance has been investigated as shown in Fig.7. It is obvious that the increase of the negative voltage applied to the acceleration electrode is accompanied by a slight difference of the extracted ion beam emittance and a sharp decrease of the extracted ion beam emittance with the increase of the positive voltage applied to the acceleration electrode.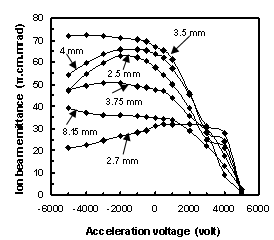 | Figure 7. Influence of the acceleration voltage on ion beam emittance for various curvatures of the convex plasma shapes without space charge without space charge |
Figure 8 shows the extracted ion beam emittance as a function of the curvatures of the plasma meniscus with different plasma shapes at acceleration voltage, Vacc = -2000 volt. The minimum ion beam emittance is found at a curvature of concave plasma shape equal 3.75 mm and a curvature of convex plasma shape equal 2.7 mm.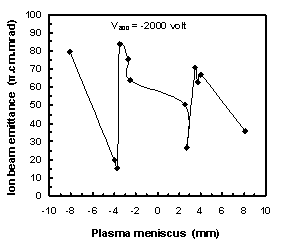 | Figure 8. Ion beam emittance as a function of the curvatures of the plasma meniscus at Vacc = - 2000 V |
Fig. 9 shows the variation of the distance between the plasma electrode and the acceleration electrode (extraction gap) on the curvature of plasma concave shape equal 3.75 mm at acceleration voltage applied to the acceleration electrode, Vacc = -2000 volt without space charge. It is found that the minimum ion beam emittance can be obtained at extraction gap equal 15.5 mm.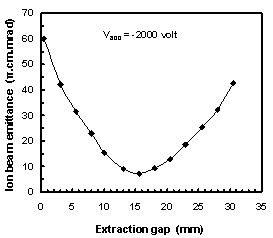 | Figure 9. Influence of the extraction gap on ion beam emittance for a concave plasma shape of 3.75 mm at Vacc = - 2000 V |
3.2. With Space Charge
SIMION supports three estimates of charge repulsion: Beam, columbic and factor repulsion. In general, charge repulsion estimations involve determining the forces between the current ion in question and all other currently flying ions. Simulation of the singly charged argon ion trajectories for a variable meniscus shape of the plasma was studied with space charge by using columbic repulsion. Columbic repulsion is estimated via point charge assumptions. Each ion is assumed to represent a point charge. In this work, simulation of the singly charged argon ion trajectories for a variable meniscus shape of the plasma is studied with space charge effect by using columbic repulsion. We deduced a relation between the current in amps. and the charge in coulombs from beam and columbic repulsion calculations as follows:Beam repulsion acceleration given by:1- The beam repulsion for each ion is assumed to represent a line charge. The line charge density (coulombs/mm) is determined by apportioning the beam current between the ion trajectories according to their charge adjusted by their charge weighting factor and dividing it by the ion’s velocity:Coulombs/mm = (coulombs/μ sec)/ (mm/μ sec).Beam repulsion requires that all the ion trajectories be flown via space coherent integration. The beam repulsion acceleration is given by: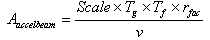
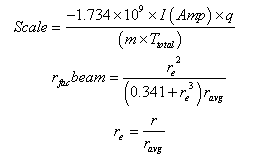 | (9) |
where Aaccelbeam is the acceleration components computed using unit vector for distance r between the two ions where:I (Amp) = total beam (amps)q = charge on current ion (real charge)m = rest mass of current ion (amu)Ttotal = sum of all ion’s cwf x their absolute chargeTg = test ion’s charge (real charge)Tf = test ion’s charge weighting factorr = distance between the two ionsravg = average min distance between ionsν = speed of the test ion2- The Coulombic repulsion for each ion is assumed to represent a point charge. The total coulombs of charge are apportioned between the ion trajectories according their charge adjusted by their charge weighting factor. The Coulombic repulsion requires that all the ions be flown in time coherent integration.The Coulombic repulsion acceleration is given by: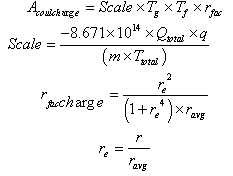 | (10) |
where:Qtotal = total coulombs of charge (coulombs)q = charge on current ion (real charge)m = rest mass of current ion (amu)Ttotal = sum of all ion’s cwf their absolute chargeTg = test ion’s chargeTf = test ion’s weighting factorr = distance between the two ionsravg = average min distance between ionsBy divided equations 9 and 10, we obtained the relation: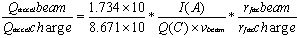 | (11) |
After calculation the third term in equation 16, we obtain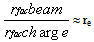 where r ≤ 5mm, thus
where r ≤ 5mm, thus 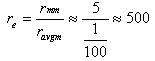 Thus the equation 16 can be presented as
Thus the equation 16 can be presented as 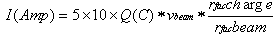 , and the speed (νbeam) of 5Kev = 1.55105 m/sThe charge repulsion between two representative ions can be represented as:
, and the speed (νbeam) of 5Kev = 1.55105 m/sThe charge repulsion between two representative ions can be represented as: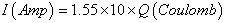 | (12) |
From equations (11), (12), the relation between the current in Amps and the charge in Coulomb is given by: 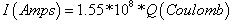 | (13) |
Fig. 10 shows the influence of the space charge on ion beam emittance at acceleration voltage Vacc = -2000 volt applied to the acceleration electrode of the triode extraction system for flat plasma. It is clear that for flat plasma, space charge has a slightly effect on the extracted ion beam emittance and started to have a large effect at current higher than10-1 A.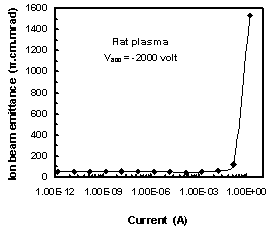 | Figure 10. Influence of space charge on ion beam emittance for flat plasma shape at Vacc = - 2000 V |
The influence of space charge on the extracted ion beam emittance for a variable curvatures of concave plasma meniscus at acceleration voltage, Vacc = -2000 volt applied to the acceleration electrode of the triode extraction system has been studied as shown in Fig .11. It is found that; the space charge has a large effect on the extracted ion beam emittance for different curvatures of concave plasma shapes at current higher than 10-4 A.Figure 12 shows the influence of the space charge on the extracted ion beam emittance for a variable curvatures of convex plasma meniscus at acceleration voltage, Vacc = -2000 volt applied to the acceleration electrode of the triode extraction system. It is obvious that no effect for space charge on the extracted ion beam emittance, till the current of 10-1 A, then the extracted ion beam emittance increased.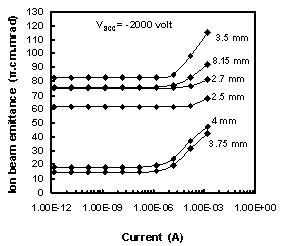 | Figure 11. Influence of space charge on ion beam emittance for different curvatures of concave plasma shapes at Vacc = - 2000 V |
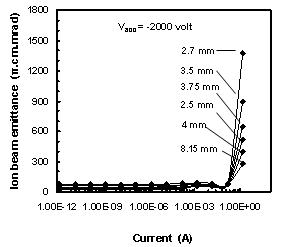 | Figure 12. Influence of space charge on ion beam emittance for different curvatures of convex plasma shapes at Vacc = - 2000 V |
4. Conclusions
The simulation of singly charged argon ion trajectories for variable curvatures of plasma meniscus is studied with and without space charge for triode extraction system using SIMION 3D version 7.0 personal computer program. The influence of the acceleration voltage (varied from –5000 to +5000 volt ) applied to the acceleration electrode of the triode extraction system on the extracted ion beam emittance have been investigated. It can be concluded that without space charge at acceleration voltage Vacc = -2000 volt applied to the acceleration electrode of the triode extraction system, the minimum ion beam emittance is found at a curvature of concave plasma shape equal 3.75 mm and a curvature of convex plasma shape equal 2.7 mm. Also the influence of the extraction gap on the extracted ion beam emittance without space charge at acceleration voltage, Vacc = -2000 volt applied to the acceleration electrode for a curvature of concave plasma shape equal 3.75 mm has been determined. It is found that the minimum ion beam emittance is obtained at extraction gap equal 15.5 mm. Also the effect of space charge on the extracted ion beam emittance for variable plasma meniscus at acceleration voltage, Vacc = - 2000 volt applied to the acceleration electrode of the triode extraction system has been studied. It is found that the space charge has a large effect on the extracted ion beam emittance for a different concave plasma shapes at current higher than 10-6 A. For flat plasma, the space charge has a slightly effect on the extracted ion beam emittance and started to have a large effect at current higher than10-1 A. But for different convex plasma shapes, there is no effect of the space charge on the extracted ion beam emittance till the current of 10-1 A then the extracted ion beam emittance increased. Also from this study, it can be concluded that the construction of the triode extraction system with extraction gap equal 15.5 mm and acceleration voltage, Vacc = - 2000 volt applied to the acceleration electrode is suitable for optimum extraction of ion beam from variable plasma meniscus.
References
| [1] | P. Spadatke, in The Physics and Technology of Ion Sources, I. G. Brown (Ed.), John Wiley, New York (1989) |
| [2] | D. A. Dahl,’SIMION 3 D Version 7.0 User’s Manual INEEEL – 95 / 0403, Idaho National Engineering and Environmental Laboratory, I D 83415 (2000) |
| [3] | D.A. Dahl, J.E. Delmore and A.D. Appelhans, Rev. Sci. Instrum. 61 (1990) 607 |
| [4] | I. Langmuir, Phys. Rev., 2, 450 (1913) |
| [5] | A. Septier, Focusing of Charged Particles, Vol. II, Academic press, New York(1967) |
| [6] | A. F. T. Holmes,’Phys. Rev. A’, 19, P. 389 (1979) |
| [7] | J. Ishikawa etal;’J. Appl. Phys.’ 53 (9), P. 6018 (1982) |
| [8] | S. A. Self,’ The physics of Fluids’, 6 (12), P. 1762 (1963) |
| [9] | R.G. Wilson and G.R. Brewer, Ion Beams with Applications to Ion Implantation, John Wiley, New York (1973) |
| [10] | I. G. Brown, ‘The physics and Technology of Ion Sources’, Wiley & Sons (1989) |
| [11] | B.H. Wolf, Handbook of Ion Sources, CRC press, Boca Raton, New York (1995) |
| [12] | M.M. Abdelrahman and H. El-Khabeary, Simulation of the plasma meniscus with and without space charge using triode extraction system, Brazilian Journal of Physics, vol. 39, 1, March, 2009. |
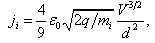
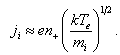
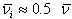 where
where 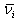 is the mean velocity of the ions after crossing the plasma sheath. The mean velocity
is the mean velocity of the ions after crossing the plasma sheath. The mean velocity 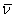 is given by:
is given by:
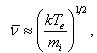
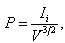


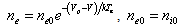
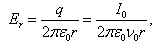
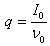 is the charge of the beam per unit length within the beam radius r, I0 is the total beam current, and
is the charge of the beam per unit length within the beam radius r, I0 is the total beam current, and 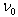 the axial ion velocity.For higher ion currents at a low acceleration voltage, the ion space charge in the extraction region is high and then the beam will diverge within a short distance if space charge is not fully compensated. When the space charge of the ion beam is compensated by electrons, no radial force affects the ion beam.
the axial ion velocity.For higher ion currents at a low acceleration voltage, the ion space charge in the extraction region is high and then the beam will diverge within a short distance if space charge is not fully compensated. When the space charge of the ion beam is compensated by electrons, no radial force affects the ion beam.
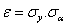
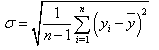
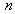 is the number of repeated measurements,
is the number of repeated measurements, 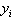 is the individual
is the individual 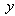 -values and
-values and 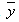 is the mean value of the repeated
is the mean value of the repeated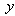 -values. For a fixed geometry of the triode extraction system, the following calculations have been done with and without space charge:
-values. For a fixed geometry of the triode extraction system, the following calculations have been done with and without space charge:




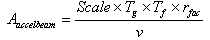
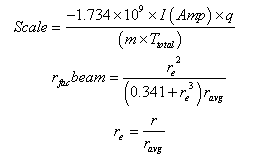
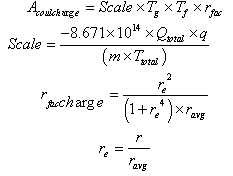
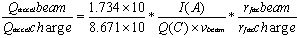
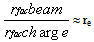 where r ≤ 5mm, thus
where r ≤ 5mm, thus 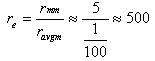 Thus the equation 16 can be presented as
Thus the equation 16 can be presented as 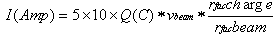 , and the speed (νbeam) of 5Kev = 1.55105 m/sThe charge repulsion between two representative ions can be represented as:
, and the speed (νbeam) of 5Kev = 1.55105 m/sThe charge repulsion between two representative ions can be represented as: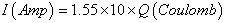
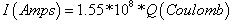



 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML