-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2012; 2(5): 101-107
doi: 10.5923/j.ijtmp.20120205.02
Laws of Nature Forbid the Existence of p = 0 Condensate in a System of Interacting Bosons
Yatendra S. Jain
Department of Physics, North-Eastern Hill University, Shillong, 793022, India
Correspondence to: Yatendra S. Jain , Department of Physics, North-Eastern Hill University, Shillong, 793022, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Analyzing the basic dynamics of two bosons, interacting through a central force, we make three unequivocal conclusions: (i). Natural laws, demanding the ground state of a system to have least possible energy, forbid the existence of p = 0 condensate in a system of interacting bosons (SIB). (ii). The ground state of a SIB, with different number of particles having different momenta does not have least possible energy as it should be. (iii). All particles in the true ground state have identically equal energy, εo = h2/8md2, and equivalent momentum, qo = π/d. The real nature of Bose Einstein condensation (BEC) that exists in the superfluid state of a SIB is identified as the condensation of particles in a state of a pair of particles having equal and opposite momenta (q, -q) with center of mass momentum, K = 0 and q = π/d. We also discuss how experimental results pertaining to the existence of electron bubble and free rotation of molecules in helium droplets and clusters support the absence of p=0 condensate and how single particle basis (SPB), having an alliance with p=0 condensate, is inconsistent with certain physical realities of the system at low temperatures. These conclusions render strong support for our theory of superfluidity of a system like liquid 4He (Amer. J. Cond. Mat. Phys. 2, 32-52(2012).
Keywords: P = 0 Condensate, BEC, Interacting Bosons, Helium-4, Trapped Dilute Gases, Superfluidity
Article Outline
1. Introduction
- In its ground state (G-state), a system of non-interacting bosons (SNIB) is shown[1, 2] to have 100% particles in the single particle state of momentum p = 0 as depicted by Fig. 1(A). These particles constitute what is known as p = 0 condensate[or Bose Einstein condensate (BEC)] whose density (np=0 = Np=0/N with Np=0 = number of bosons having p = 0 and N = total number of bosons in the system) decreases smoothly with increase in temperature (T) from np=0 = 1.0 at T = 0 to np=0 = 0 at T = Tc (the temperature of the onset of BEC) by following np=0 =[1 – (T/Tc)3/2]. However, no system of bosons of finite mass (m), found in nature, represents a SNIB. They all represent a system of interacting bosons (SIB) and some such systems viz., liquid 4He, trapped dilute gases (TDG), etc., are found to exhibit a BEC whose real nature is still unclear. As per a common belief, guided by Bogoliubov’s theory of weakly interacting bosons[3], Np=0 gets depleted because the repulsive component of inter-particle interaction pushes a fraction of N particles to p ≠ 0 states and particles in the G-state of a SIB are believed to have their momentum distribution, N(p), as depicted in Fig.1(B). Formulation of conventional microscopic theories (reviewed in[4-6]) of liquid 4He and TDG is clearly guided by the presumed existence of p=0 condensate in their low T phases and this idea has been strengthened by several theoretical and experimental studies concluding that np=0 in He-II (superfluid 4He) and BEC state of different TDGs falls, respectively, around 10%[1,2] and 60% or more[5, 6] depending on the density of bosons and the strength of their interactions. However, several experts in the field (viz. Glyde and Svensson[7], Sokol[8] and Leggett[9]) also believe that the existence of p = 0 condensate in superfluid 4He has not been established by any experiment beyond a point of doubt, since the expected δ-peak in N(p) at p = 0 could not be observed in spite of several experimental studies of neutron inelastic scattering from He-II[7, 8]. Guided by this fact Leggett[9] made an important remark. He states, “In the sixty years since London’s original proposal, while there has been almost universal belief that the key to superfluidity is indeed the onset of BEC at Tλ, it has proved very difficult, if not impossible, to verify the existence of the latter phenomenon directly. The main evidence for it comes from high energy neutron scattering and, very recently, from the spectrum of atoms evaporated from the liquid surface and while both are certainly consistent with the existence of a condensate fraction of approximately 10%, neither can be said to establish it beyond all possible doubts.” We may also mention that most researchers in the field are aware of the fact that the presumption of the existence of p = 0 condensate in He-II has failed to render a viable theory that explains its properties at quantitative scale in spite of the fact that numerous efforts have been made over the last 75 years. While this speaks of the problems with the conventional belief that superfluidity and related properties of He-II arise due to presumed existence of p=0 condensate, no effort has been made to identify them. This motivated us to make our efforts to find the said problems and their source to facilitate the development of the long awaited theory of liquid 4He type SIB[10] and establish the results of our critical study of two body wave mechanics[11] which provides necessary foundation to[10]. Concluded, unequivocally, by a simple analysis reported in this paper, the laws of nature are found to exclude the existence of p = 0 condensate and the conventional form of N(p)[Fig.1(B)] from the G-state of a SIB. In what follows, not even a single particle has zero momentum in the G-state of a SIB implying that the question of a macroscopically large number of bosons having p=0 does not arise. In fact all particles in the G-state of a SIB are concluded to have identically equal energy, εo = h2/8md2 (Eqn. 6, below), as zero-point energy and equivalent momentum, p = h/2d (with h being the Planck constant and d = v1/3 where v = V/N is the volume per particle)[Fig.1(C)]. Once this reality finds its acceptability with people, who have been working untiringly for the last several decades to find the theory of superfluidity of liquid 4He type systems, it is expected to bring drastic change in the microscopic understanding of widely different many body quantum systems, viz., TDGs, liquid 3He, electron fluid, etc.
2. Analysis and Discussion
- In what follows from[3-6], different number of atoms even in the G-state of a SIB have different momenta, k1, k2, k3, ....., kN (with their magnitudes expressed in wave number), ranging from k = π/L to its large multiples (order of N1/3) with L = size of the container. Although, k = π/L is not zero in its true sense even for macroscopically large L, however, in practice it is equated to zero for valid approximation and we do not question its validity. But in wave mechanics other details of the state (such as the wave function) also have their own importance and as shown in this paper (cf. Section 4), this is really true in present case in order to compare the nature of BEC in a SIB and in a SNIB. It is clear that nk=0 can be used for np=0. Since the microscopic theories[3-6], which conclude the above stated details of the G-state, use single particle basis (SPB) in a sense that particles in the system are assumed to occupy states of a single particle confined to volume V of the system (or a single particle is assumed to represent the basic unit of the system), we identify its concluded G-state[Fig.1(B)] as G-state(SPB) and corresponding energy as Eo(SPB). It may be mentioned that in Fig.1, we identify levels of a particle by the magnitude (p) of its momentum p (a vector which has magnitude as well as a direction), not by its energy, to keep consistency with the use of “p = 0 condensate′′ in common practice. This choice is also consistent with the fact that every direction of p is equally probable.To a good approximation, particles in a fluid move freely over a surface of constant potential (V = 0 for gases and V = −Vo for liquids) unless they collide with each other or with the walls of the container and this remains valid even for the G-state of a SIB, such as, liquid 4He which retains fluidity even at T = 0. Since −Vo is decided mainly by the density of particles and the details of inter-particle interactions (not by the momenta of particles) and the density does not change significantly for a SIB like liquid 4He[12] when its T changes from T = Tλ to T = 0 (i.e., for the superfluid state of the system), it is clear that only the momentum distribution of particles should ensure minimum of the kinetic as well as total energy of the particles.It is well known that the dynamics of two particles (say, P1 and P2 interacting through a two body central force), moving with momenta, k1 and k2, in the laboratory frame, can always be described in terms of their relative momentum k = 2q = k2 − k1 , and CM momentum K = k1 + k2, as we have
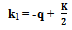 | (1) |
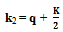 | (2) |
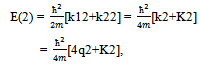 | (3) |
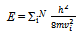 | (4) |
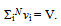 | (5) |
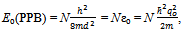 | (6) |
3. True G-state
- The above analysis quiet neatly concludes that: (i) the G-state(SPB) of a SIB (with different number of particles having different momenta as depicted by Fig.1(B)) is not an acceptable G-state because it does not have minimum possible energy and (ii) particles in the true G-state[which may be identified as G-state(PPB)] have identically equal energy with K = 0 and q = qo = π/d (Fig.1(C)). Evidently, not even a single particle in the true G-state of a SIB has a p < h/2d (or energy < h2/8md2). Naturally, the question of macroscopically large number of particles having p = 0 does not arise which means that the presumption of the existence of p = 0 condensate in the superfluid state of a SIB[3-6] is not valid. This conclusion has great relevance for superfluidity and related properties of He-II and similar state of different TDG, particularly, since the configuration of G-state(PPB) is retained[10] by the system at all T < Tλ. It renders a reason for which the existence of p = 0 condensate in He-II has not been experimentally observed beyond a point of doubt[7, 8]. In addition since each particle in G-state(PPB) occupies a cavity of size d with identically equal value of nearest neighbor separation r = d, particles in this state make a close packed arrangement of their wave packets (CPA-WP) which allows particles to move only in order of their locations. The fact that each particle has q=qo=π/d, reveals that the locations of two particles on the line of their relative phase (φ = kr) differ by Δ φ = 2nπ (with n = 1, 2, 3, .. … …) indicating that particles in the superfluid phase of a SIB move coherently (fixed value of Δφ) provided their motion does not disturb the G-state configuration. We note that all these aspects of the G-state(PPB) can be associated qualitatively to superfluidity and related properties of He-II. For example, (i) the fact that particles in He-II cease to have relative motions can be identified with the loss of viscosity, (ii) the fact that all particles occupy a single energy state easily explains zero entropy, (iii) the fact that particles maintain definite phase relationship Δφ = 2nπ provides strong foundation to experimentally observed coherence of their motion and quantized vortices, (iv) the CPA-WP which closely resemble with an orderly arrangement of particles with no vacant site can be related to experimentally observed infinitely high thermal conductivity of He-II; the arrangement should, however, not be confused with crystalline structure where particles occupy rigidly fixed positions. In our recent paper[16], we discuss this CPA-WP in detail and conclude that the arrangement is not expected to show up its signature in experiments related to diffraction of particles (photons, electrons and neutrons) from He-II because 4He atoms have vanishingly small shear forces due to its fluidity; the arrangement remains highly fragile for small energy perturbation. Detailed account of different aspects of superfluidity and related properties of He-II can be found in[10].
4. Real Nature of BEC
- By taking two particles as a pair, this study concludes that each particle in the system is a part (or a representative) of a pair of particles moving with equal and opposite momenta (q, -q) with respect to their CM which moves with momentum K in the laboratory frame. In other words it identifies a pair of particles as a basic unit of a SIB and this is consistent with the fact that particles in a SIB interact through a two body interaction, particularly, because a system in its ground state has nothing but potential energy. Even the residual KE of particles (εo = h2/8md2) also serves as a source of their zero point repulsion for its dependence on d; in a sense this is identical to a two body repulsion. The zero point repulsion clearly dominates the low T behavior of liquid 4He as it does not allow the liquid to assume its solid phase even at T=0 unless the liquid is subjected to an external pressure of about 30 atmosphere. The repulsion also forces the liquid to suddenly expand on its cooling through Tλ[10]. Interestingly, even the SPB based theories[4-6] use pairs of particles to evaluate the contribution of inter-particle interactions to the energy of a SIB, the use of single particle description is kept intact. However, as we find, we must use PPB (not SPB) to describe a SIB at least in its low T states and this implies that the real nature of BEC in the superfluid phase of a SIB is the condensation of its particles as (q,-q) pairs in its G-state characterized by K = 0 and
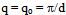 .It is interesting to compare these results with corresponding results known for a SNIB having same N and V. We note that a SNIB is a special case of a SIB where inter-particle interactions have been switched off. Since a particle in such a system has no means to identify the presence of other particles, each of the N bosons behaves like the lone particle trapped in the container. Naturally, the energy level where all such bosons have to condense does not differ from the lowest energy level of a single particle kept in a box (say a cubical box of size L) and this corresponds to an energy as low as εo(SNIB) = h2/8mL2 or equivalent momentum as low as qo(SNIB) = π/L. These values are conventionally believed to be as good as zero, while it is evident that in their absolute meaning they are non-zero. When εo(SNIB) and qo(SNIB) are compared with our results (Eqn.6), εo(SIB) = h2/8md2 and corresponding momentum qo(SIB) = π/d) then it becomes clear that εo(SIB) is L2 /d2 times higher than εo(SNIB) and qo(SIB) is L/d times higher than qo(SNIB). Assuming that we have 1024 particles of each type in separate containers of volume V we find that εo(SIB)/εo(SNIB) ≈ 1016 and qo(SIB)/qo(SNIB) ≈ 108. This speaks of the order of impact of hard core interaction of particles on the characteristics G-state energy and equivalent momentum of a particle. Evidently, hard core interaction makes particles to share V equally, particularly, in their superfluid phase, and each one behaves like a particle trapped in a box of size d, while non-interacting bosons (unaware of the presence of each other in the box) behave like a particle trapped in box of size L. Thus the BEC in a SIB and that in a SNIB are characteristically identical; in the former the G-state is characterized by qo = π/d, while in the latter by qo = π/L. Since the BEC in a system represents a macroscopic condensation of particles in its G-state, we also note following similarities in both cases: (i) the G-state wave function that represents a particle is a state of the superposition of two plane waves of momenta q, and -q (with q = qo ) (synonym with a state of pair of particles having equal and opposite momenta[10, 11]), (ii) while the momentum of a particle in such a state is not a good quantum number, its magnitude qo is obtainable from corresponding εo, and (iii) the expectation value of the momentum operator in these states is zero, i.e., < p >= ћ< q >= 0. Since all these inferences could be drawn only by using the details of the ground state wave function of the pair[10,11], it shows the importance of knowledge of the said function in identifying the correct nature of BEC. Evidently, BEC in systems confined to finite V (it may be SIB or SNIB) occurs in a state of p = ћqo or of < p > = 0, but not of p = 0.
.It is interesting to compare these results with corresponding results known for a SNIB having same N and V. We note that a SNIB is a special case of a SIB where inter-particle interactions have been switched off. Since a particle in such a system has no means to identify the presence of other particles, each of the N bosons behaves like the lone particle trapped in the container. Naturally, the energy level where all such bosons have to condense does not differ from the lowest energy level of a single particle kept in a box (say a cubical box of size L) and this corresponds to an energy as low as εo(SNIB) = h2/8mL2 or equivalent momentum as low as qo(SNIB) = π/L. These values are conventionally believed to be as good as zero, while it is evident that in their absolute meaning they are non-zero. When εo(SNIB) and qo(SNIB) are compared with our results (Eqn.6), εo(SIB) = h2/8md2 and corresponding momentum qo(SIB) = π/d) then it becomes clear that εo(SIB) is L2 /d2 times higher than εo(SNIB) and qo(SIB) is L/d times higher than qo(SNIB). Assuming that we have 1024 particles of each type in separate containers of volume V we find that εo(SIB)/εo(SNIB) ≈ 1016 and qo(SIB)/qo(SNIB) ≈ 108. This speaks of the order of impact of hard core interaction of particles on the characteristics G-state energy and equivalent momentum of a particle. Evidently, hard core interaction makes particles to share V equally, particularly, in their superfluid phase, and each one behaves like a particle trapped in a box of size d, while non-interacting bosons (unaware of the presence of each other in the box) behave like a particle trapped in box of size L. Thus the BEC in a SIB and that in a SNIB are characteristically identical; in the former the G-state is characterized by qo = π/d, while in the latter by qo = π/L. Since the BEC in a system represents a macroscopic condensation of particles in its G-state, we also note following similarities in both cases: (i) the G-state wave function that represents a particle is a state of the superposition of two plane waves of momenta q, and -q (with q = qo ) (synonym with a state of pair of particles having equal and opposite momenta[10, 11]), (ii) while the momentum of a particle in such a state is not a good quantum number, its magnitude qo is obtainable from corresponding εo, and (iii) the expectation value of the momentum operator in these states is zero, i.e., < p >= ћ< q >= 0. Since all these inferences could be drawn only by using the details of the ground state wave function of the pair[10,11], it shows the importance of knowledge of the said function in identifying the correct nature of BEC. Evidently, BEC in systems confined to finite V (it may be SIB or SNIB) occurs in a state of p = ћqo or of < p > = 0, but not of p = 0. 5. Inter-particle Correlation
- In principle, fixing of N particles at their positions requires fixing of only N points, while fixing of N(N−1)/2 CM points by using K=0 condition (as inferred in Section 2) for each pair is far more than N. Since N(N−1)/2 ≥ N is true for N ≥ 3, fixing of N(N−1)/2 CM points naturally ensures fixation of the positions of N particles except for a system of N = 2 which has only 1 CM point; one cannot fix the positions of two particles or their 6 degrees of freedom by fixing the position of only 1 CM point, -equivalent to fixing only 3 degrees of freedom and leaving 3 degrees of freedom (two rotations and one vibration) unfixed. However, our problem at hand is related to many particle system, we leave N = 2 case as an exception to which following discussion and its inferences may not apply. As the coordinates of each CM point are related to the position coordinates of two chosen particles, positions of all the N(N−1)/2 CM points get automatically fixed if we fix the positions of N particles and vice versa. We understand that N particles have only N independent momenta. However, when we make their pairs we have N(N−1)/2 different relative motions with corresponding relative momenta plus the same number of CM motions with corresponding CM momenta which make a total of N(N-1) different momenta (much higher than N independent momenta). But it is not surprising because the relative and CM momenta depend on k1, k2, k3, .... kN momenta of N particles since each particle makes (N − 1) pairs with rest of the N-1 particles indicating that k1 momentum of a particle (say P1) appears in the definition of N-1 relative momenta and N-1 CM momenta; the same is true when another particle is counted to make new (N −2) pairs and so on. Evidently, any change in the momentum of one particle disturbs the relative and CM momenta of (N−1) pairs and this speaks of the order of momentum correlation between all particles if the system has to be described in terms of pairs. Naturally, when the use of SPB becomes inapplicable for the low T states of the system, momentum correlation can be seen between any two or any three or any four or …. particles located at any distance (as large as the size of the system); this becomes more prominent, particularly, when the system is in its G-state where all particles are restricted to have r= d, q=qo, and K=0 as an addition condition. Evidently, any change in q and K of a single particle (cf. Eqns. 1 and 2) from these values would disturb the condition of minimum energy satisfied by the G-state and all the N-1 pairs of particles would appear to have relative momenta different from k=2qo and CM momenta different from K=0. Interestingly, this correlation emerges as a basic aspect of the superfluid state of the system, since the G-state configuration persists over the temperature range from T = 0 to T = Tλ as concluded in[10]; it is obvious that q-correlations are not different from the correlation of corresponding energy. Since inter-particle distance (d) between two nearby particles in the G-state is related to their wave packet size through, d = λ/2 = π/q, similar correlations are expected between r-positions (φ-positions) of two or more particles when r deviates from d and Δφ deviates from 2n π. As shown in[10], all these correlations are consistent with experimental observation of quantized vortices, second sound (propagation of temperature fluctuations as waves), etc.[1, 2].
6. SPB and Its Inconsistency
- In section 2 we concluded that p = 0 condensate, which can be defined only when one uses SPB to describe a SIB, is not consistent with the basic laws of nature. In this section we proceed further to show how SPB used in constructing the conventional microscopic theories, which assume the existence of p=0 condensate as an important factor responsible for superfluidity and related aspects of superfluid SIB, is inconsistent with certain physical realities of a SIB at low T. As discussed in[10], two nearby particles assume a state of their wave superposition, -as an obvious consequence of wave particle duality, when their thermal de Broglie wave length, λT = h/√(2πmkBT)[1, 2, 13] (with kB being the Boltzmann constant), becomes larger than d. We discuss the details of the wave superposition of two quantum particles in[10, 11] and discover that such a state cannot be described by a plane wave used to describe a system under SPB; the state should rather be represented by a superposition of two plane waves which either represent two different particles or a single particle in states of two different momenta[10,11]. The state, in the former case, describes what we call as mutual superposition of two different particles, while in the latter case it describes a state of self superposition of a particle which is physically possible if a wave representing a particle has its superposition with its own reflection or scattering from other particle(s) or the boundary walls of the container[10,11]. Interestingly, as discussed in[10,11] , there is no means to ascertain whether two particles, in the process of their collision, have their mutual superposition or their self superposition. In what follows each particle in the state of their wave superposition, represents a pair of particles described by a pair wave form[10,11], Ψ(1,2) = sin(q.r) exp(iK.R) which does not represent an eigen state of the momentum operators of individual particle in the pair or even the relative momentum of the pair. Since the momenta of individual particles do not remain good quantum numbers in this state, it is clear that SPB (where momentum of individual particle remains a good quantum number) is inconsistent with the wave superposition (an obvious physical reality of the system at low T).
7. Experiments and p=0 Condensate
- More recently several experimental observations have been found to corroborate our inferences regarding the true G-state of a SIB and the real nature of BEC in its superfluid phase. One such observation is the linear Stark effect of roton transition seen through the microwave absorption in He-II[17]. The observation cannot be understood in terms of N(p) (Fig.1(B)) where 4He atoms in He-II are assumed to have random motions since such motions do not allow the atomic dipoles to have their ordered arrangement necessary to explain the observation[16]. Thus the observation not only supports the true G-state of a SIB concluded here but also proves the absence of p=0 condensate. The other experimental realties that support these inferences are discussed in the following: (i). Existence of an electron bubble: An excess electron in liquid helium exclusively occupies a self created spherical cavity (known as electron bubble) of certain radius, when it assumes its G-state in the bubble. To create the bubble, the electron exerts its zero-point force fo = h2/4medb3 (where me = mass of the electron and db = diameter of the bubble) on the surrounding 4He atoms against the forces originating from inter-atomic interactions and external pressure on the liquid[18]. It is well known that the bubble formation is a consequence of the facts that: (i) an excess electron experiences a strong short range repulsion with 4He atoms which forbids its binding with them and (ii) the electron, for its quantum nature, manifests itself as a WP whose size λ/2 increases with the decrease in its energy. This implies that any quantum particle that experiences similar repulsion with 4He atoms should have similar state in liquid helium and this is found to be true with positron[19] and other particles (ions, atoms, molecules, etc.[20]). These observations, naturally, lead one to believe that each 4He-atom in He-II should also assume similar state when it occupies its lowest possible energy because it is also a quantum particle and experiences strong short range repulsion with other 4He atoms. This means that each 4He atom in He-II should occupy a spherical cavity of size equal to the size of its wave packet and retain a non-zero value of its zero point energy (or equivalent zero point momentum) rather than zero energy/momentum. Evidently, the physical reality of the existence of electron bubble indirectly proves the absence of any 4He atom with p=0 and hence the absence of p=0 condensate in He-II. (ii) Spectroscopy of molecules embedded in He-droplets or clusters: Experimental study of high resolution rovibrational spectra of embedded molecules (e.g., OCS/N2O molecule in 4He droplets and 4Hey:OCS or 4Hey:N2O clusters[21] where y = number of 4He atoms) provides another strong support to the absence of p=0 condensate in low T phase of a SIB. These studies further prove that superfluidity and related aspects of any SIB has no relation with p = 0 condensate since 4He atoms in these systems are confined to a space of size, s ≈ 5Ǻ for which each atom is expected to have reasonably high momentum ≈ π/s rather than p=0. Further since each cluster is expected to have certain stable structure (which of course would depend on inter-particle interactions and may change with change in y), the embedded molecule sees a time independent potential which implies that 4He atoms around the rotor cease to have collisional motions. In other words 4He atoms in these droplets and clusters are localized with position uncertainty decided by their least possible momentum of their confinement and this agrees closely with our conclusions in Section 3.
8. Concluding Remarks
- A simple analysis of two body dynamics unequivocally concludes that the existence of p = 0 condensate, presumed as one of the basic foundations of superfluidity of a SIB (as reviewed in[4-6]), violates the basic fact that the ground state of a system has to have least possible energy. In the true ground state of a SIB all particles have to have identically equal energy (εo = h2/8md2)[or equivalent momentum qo = π/d]. In what follows from the arguments behind Eqns. (4 and 6) these results are consistent with an obvious condition known as excluded volume condition[22] which states that each particle such as 4He atom occupies certain volume exclusively due to its short range hard core (HC) repulsion for neighboring particles. While experiments on He-II and BEC state of different TDG undoubtedly indicate the presence of a phase like BEC, this study establishes that p = 0 condensate[as depicted in Fig.1(B)] is not the true form of the said BEC; rather, it is a macroscopic condensation of pairs of bosons in a state of their K = 0 and q = qo. As we find, our PPB based theory[10] of a SIB concluding a G-state, that agrees fully with the inferences of this analysis, provides a good quantitative account of superfluidity and related properties of liquid 4He[23-27]. In our recent study[16] which analyzes the origin of the experimentally observed Stark effect in microwave absorption by rotons in He−II[17], we clearly discover that the observation renders strong experimental support for : (i) the absence of p = 0 condensate and (ii) the G-state(PPB) concluded in this paper. These inferences are also supported by the observation of the quantum evaporation of 4He atoms from the surface of He-II (induced by a beam of phonons and roton excitations) as shown recently by us[27]. We find that conventional many body theories have been encountering serious difficulties in achieving desired success primarily for their use of SPB which is clearly not consistent with wave superposition of particles, -an important physical reality of the system at low T. Apparently, it is for this reason that SPB based theories of superconductivity (including BCS theory[28]) too could not be found to have expected accuracy. We may finally mention that this study along with our recent studies[10,11, 16, 26, 27] may bring a revolutionary change in the microscopic understanding of superfluidity and similar phenomena such as superfluidity of liquid 3He, superconductivity, etc. This would also help in unifying the physics of widely different systems of interacting bosons and fermions including, atomic nuclei, neutron stars, etc.
ACKNOWLEDGEMENTS
- The author is thankful to Drs Bimalendu Deb (IACS Kolkata), R. P. Bajpai (NEHU, Shillong) and S. Aravamudhan for fruitful discussions.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML