Ohochuku N. Stephen
Department of Chemistry, Rivers State University of Education, P.M.B 5047, Port Harcourt Nigeria
Correspondence to: Ohochuku N. Stephen , Department of Chemistry, Rivers State University of Education, P.M.B 5047, Port Harcourt Nigeria.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Illustrations and questions based on the equation “heat gained equals heat lost” have always been restricted to mixing systems at two different temperatures. This article shows how to extend the above equation to systems with more than two different temperatures. Using the current formula the following procedures are generated. The method of mixing two systems at a time (pair mixing) is illustrated. The technique of taking any of the systems (preferably the one with the lowest temperature) as the only heat gainer is also illustrated. A new formula based on constancy of heat content is introduced. The various methods are tested and found to be perfect and should be incorporated into the teaching and learning in this aspect of heat study.
Keywords:
New Formulas, Temperature Determination, Mixed Systems
1. Introduction
Heat is a form of energy commonly associated with other forms of energy and processes especially those involving motion. In most cases there is always a temperature change when a body absorbs or dissipates heat[1]. Heat has been variously described as energy that increases or decreases the temperature of a body absorbing or dissipating it. Anyakoha[2] describes heat as energy associated with a temperature difference. These show the inter relationship of heat and temperature. However, not always does a body’s temperature change on absorption or dissipation of heat[3] as is the case when a body is undergoing a phase change (e.g. at melting point, boiling point or transition point). The energy absorbed by the body at this point does not lead to increase in the temperature of the body because the energy is used to free the atoms and molecules from strong inter atomic and intermolecular forces leading to gain in potential energy that result to change in phase[4,5]. For a body undergoing phase change at the transition temperature, specific heat capacity is zero but heat capacity is not zero, so specific heat capacity is a characteristic of a phase. The heat absorbed at this transition temperature is called the latent heat. With the above facts, heat is more appropriately defined as the energy that increases the total internal energy of a body absorbing it[1,3,5]. Temperature which has been described as a measure of degree of hotness or coldness[2,3,4] is an intensive property, and properly defined, is a measure of the average kinetic energy of the atoms and molecules of a body[5]. When two bodies at different temperatures are in contact and conduct heat, heat flows from the body at high temperature to the one at low temperature until the two bodies attain a constant temperature. Such constant or resulting temperature has always been calculated using the law of conservation of heat energy and for mixtures the law is expressed in the form of the equation, ‘Heat gained = heat lost’. The law is of general application so also should be the equation but the illustrations and examples have always been restricted to mixing of bodies at only two different temperatures where the heat gainer or loser is obvious from the temperature values. No attempt has been made to show how to apply the law or the equation to a mixture resulting from mixing many bodies at different temperatures. One obvious reason could be that with more than two bodies, the bodies with temperatures in between the lowest and highest temperatures cannot be categorically classified as heat gainers or losers before mixing not until the temperature of the mixture is determined. Also when the systems to be mixed are of different materials and at same temperature, the heat loser or gainer is not discernable. So there is need to seek other methods that are applicable to mixing any number of systems at same or different temperatures. As of now only the existing formula is in use and only for systems at two different temperatures. It is the aim of this article to show how the existing formula “Heat gained equals Heat lost” can be extended to mixing two or more different systems with dissimilar temperatures and to use the existing formula to generate other formulas applicable to mixing two or more bodies at two or more different temperatures.
2. Methodology
2.1. Generating Equations for the New Methods
In many text books[1,2,3,4,5] to mention a few, illustrative examples and exercises in the calorimetric study of heat have always been restricted to mixing bodies at only two different temperatures applying the equation “heat gained = heat lost”. This procedure can be applied to mixing bodies at more than two different temperatures via the pair mixing method that utilizes the method in vogue as follows. Consider n bodies each of mass m1, m2, m3, …. mn, specific heat capacity (sp ht) s1, s2, s3, …sn and at temperature t1, t2, t3, … tn being mixed in the sequence (m1+ m2); (m1 + m2) + m3; (m1 + m2 + m3) + m4; (m1 + m2 + m3 + m4) + m5; and so on (i.e. pair mixing). Let t1 < t2 < t3…. < tn. By the equation “heat gained = heat lost”, let ta be the temperature of this first mixture.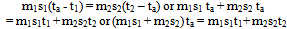 | (1) |
This first mixture of heat capacity (m1s1 + m2s2) at temperature ta is mixed with m3 to get a second mixture at tb. Hence (m1s1 + m2s2)(tb – ta) = m3s3(t3 – tb) or 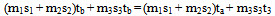 | (2) |
From (1) (m1s1 + m2s2)ta = m1s1t1 + m2s2t2, hence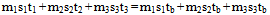 | (3) |
In general if tf is the final temperature of the mixture 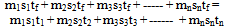 | (4) |
Equation (4) will be used to generate various general methods applicable to mixing bodies at two or more different temperatures as follows. For simplicity let n = 3.
2.1.1. One Body Heat Gainer or Looser Method
For a mixture of three bodies, n = 3. So (4) reduces to (4a).  | ..(4a) |
Assuming m1 is the only heat gainer i.e. make m1s1(tf -t1) the subject of the equation in (4a) to get (4b).  | (4b) |
In the same equation, in the same manner, if m1 is the only heat loser, then make m1s1(t1 – tf) the subject of equation (4a) to obtain equation (4c)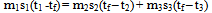 | (4c) |
Equations (4b) or (4c) is used in the “one body heat gainer or loser” method and affords a means of extending the current method to any number of bodies being mixed by assuming that any one body (preferably the body at the lowest temperature) gains heat and the rest loose heat and the general heat gained equals heat lost is applied. This method is illustrated by solution A(i) and B(i) in figure 1.
2.1.2. Heat Content Method
In equation (4), the left hand side (LHS) is the sum of the various final heat contents making up the total heat content of the resulting mixture and the right hand side (RHS) the sum of the initial heat contents of the bodies. This introduces a new method based on heat content method with the equation ‘sum of final heat content = sum of initial heat content’ where heat content of any body is the product of its mass, sp ht capacity and its temperature i.e. heat content = mst or heat capacity times t, where heat capacity of a body is ms. This process involves calculating the sum of final heat content at tm (hereafter the mixture temperature) and equating it to the sum of initial heat content as the equation stipulates. This is illustrated in solutions C(i) in figure 2.
2.1.3. Heat Content Method with Assumed Mixture Temperature Ta
For a wider application of the heat content procedure, the resulting mixture temperature tm is replaced with an assumed mixture temperature ta which can be any temperature from the low to the high phase change temperature of the liquid body of the mixture. The replacement of tm with ta in equation (4) gives equation (4d) for n = 3. 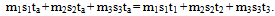 | (4d) |
Since all the terms in equation (4d) are known, if the sum of the initial heat contents minus the sum of the heat contents at ta is zero, ta is same as tm, if not the difference (positive or negative) is divided by the sum of the heat capacities of the systems at the assumed mixture temperature and the quotient (is in temperature units) added to the assumed mixture temperature to obtain the actual mixture temperature.The detailed method follows the steps: (a) Choose an assumed mixture temperature ta as stated above. (b) Calculate the sum of (i) the heat capacities of the bodies at ta (ii) initial heat contents of the bodies (iii) the heat contents at ta. (c) Subtract the sum of the heat contents at ta from the sum of the initial heat contents of the systems. (d) Divide the difference by the sum of the heat capacities and add the quotient (temperature) to ta to obtain the required mixture temperature as illustrated in solutions D(i) and E(i) to questions in figure 3.
2.1.4. Heat Content Method with Assumed Mixture Temperature Ta Equals Upper or Lower Phase Temperature of The Liquid Content of the Mixture
It is possible that the final mixture temperature from step (d) above is higher than the upper transition temperature (of vaporization) or below the lower transition temperature (of fusion) of the liquid content of the mixture, this shows that part of the liquid has evaporated (higher temperature) or still in solid state (lower temperature). The amount of liquid evaporated or still in solid state needs be known and this involves a recalculation. To avoid this recalculation, ta will be taken as any of the phase change temperatures and this introduces the heat content method which utilizes the assumed mixture temperature ta as the same as the upper or the lower phase change temperature of the liquid content of the mixture. In the heat content method with assumed mixture temperature ta equals upper or lower phase temperature of the liquid content of the mixture; the procedure is followed as in 2.1.3 up to step d. If the operation in step d is negative ( for ta = 0℃ say for ice to water) the mixture temperature is 0℃ and the mass of ice not melted is the absolute value of the difference from step c above divided by the appropriate latent heat of fusion. If the operation in step d is positive (for ta = 100℃say for water to steam) the mixture temperature is 100℃and the mass of water evaporated is the positive value of the difference from step c above divided by the appropriate latent heat of evaporation. The whole procedure is illustrated in the solutions F(i) and G(i) of sample questions in figure 4. Table 1 summarizes the various new methods.| Table 1. Summary of new methods for estimating temperature of mixed hot bodies at two or more different temperatures |
| | New Method | Formula and briefs | | Pair mixing | Utilizes the formula in vogue by mixing any two bodies first, mixes this first mixture with a third body and continues so till the last body is utilized. Mathematical handling of this method generated the equation from which other methods are hinged. | | One body heat gainer or loser | Heat gained (or lost) by any one body = Heat lost (or gained) by the other bodies | | Heat content | Sum of initial heat content of bodies = Heat content of mixture. | | Heat content with assumed temperature ta | Sum of initial heat content = sum of heat content at ta. If LHS – RHS = 0, tm = ta. If LHS – RHS = ±ve, tm = ta ± (LHS – RHS)/sum ht capacity of mixture. | | Heat content with assumed temperature(i) ta = upper transition temp of the liquid in the mixture (e.g. 100℃ for water).(ii) ta = lower transition temp of the liquid in the mixture (e.g. 0℃ for water). | Formula is as above.If tm is +ve, tm = ta and mass of liquid evaporated is (LHS – RHS)/sp latent ht capacity of evaporation of the liquid in the mixture.If tm is -ve, tm = ta and mass of ice not melted is absolute value of (LHS – RHS) ÷ sp latent ht capacity of fusion of the solid melting to liquid in the mixture. |
|
|
3. Results and Discussion
Same and or different sample questions (A to G) have been solved using the new methods introduced above as illustrations. Figure 1 shows the use of one body heat gainer or loser method, figure 2 heat content procedure, figure 3 heat content with assumed mixture temperature and figure 4 heat content method but with assumed appropriate transition temperature.
3.1. Generating Equations for the New Methods
Equation (4) which is the base on which the new methods or formulas are derived is based on the method in vogue and therefore the new methods are correct. This process of mixing the bodies in steps of two (here called “Pair mixing procedure”) mixes bodies at more than two different temperatures. It is lengthy but is a suitable check method for authenticating answers from any of the other methods hence its inclusion in some of the figures e.g. A(ii) and B(ii) of figure 1.
3.1.1. One Body Heat Gainer or Loser Method
Figure 1 below shows the application of one body heat gainer or loser method. This procedure is proven correct by solutions A(i) in figure 1. The mixture temperature tm is 60.8℃ showing ice at 0℃ and copper at 50℃ as heat gainers instead of only ice. Also solution B(ii) of figure 1 buttresses the method because all the bodies are of equal temperatures but the method assumed one of them as the heat loser. | Figure 1. Solutions of sample questions by one body heat gainer or loser method |
3.1.2. Heat content Method
Heat content equation is a thermodynamic law. Just as the principle of heat gained equals heat lost, the total final heat content will be equal to the total initial heat content which is also expressed mathematically in the expanded form as in equations (1) or (2) or (3) or (4). The principle of mixing that utilizes the equation heat gained equal heat lost is based on the assumption that the mixing is done adiabatically in which case no heat or matter leaves or enters the system. This being the case the final heat content of the mixture is equal to the sum of the initial heat contents (that is the law of conservation of heat). Figure 2 below shows the application of the heat content method. | Figure 2. Solution of sample question by the Heat content method |
3.1.3. Heat content method with assumed mixture temperature ta
The heat content method with assumed mixture temperature ta is not much different from the simple heat content method only that it has the advantage of detecting liquid eg water evaporated or residual ice in the mixture when ta is either of the transition temperatures. The method of solution using an assumed mixture temperature is illustrated in figure 3 below.The choice of an assumed mixture temperature ta in the region where specific heat capacity is not zero is because sum of heat capacities will be needed in the calculation of mixture temperature tm and the liquid body is the one to evaporate or be produced from its solid. A positive heat difference from sum of the initial heat contents of the systems minus the sum of the heat contents of the bodies at the assumed temperature indicates a surplus heat for raising the temperature of the mixture above ta by an amount equal to the positive heat difference divided by the sum of heat capacity of the mixture and this quotient is added to ta to get the mixture temperature tm. A negative heat difference treated similarly gives the mixture temperature tm as illustrated in solutions D(i) and E(i) in figure 3. 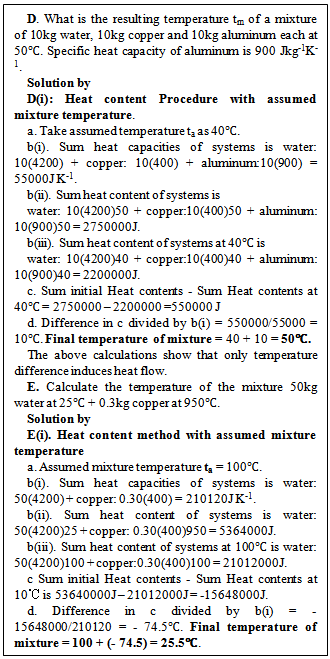 | Figure 3. Solutions of sample question by heat content method using an assumed mixture temperature Sample questions |
3.1.4. Heat content method with assumed mixture temperature ta as the upper or lower phase transition temperature of the liquid content of the mixture
In continuation of 3.1.3 above, where ta equals the upper transition temperature e.g. 100℃ for water or the lower transition temperature e.g. 0℃ for water, a positive heat difference (for ta = 100o water) evaporates mass of water equal to the positive heat difference divided by the specific latent heat of evaporation of water and a negative heat difference indicates that heat is still needed to melt more ice of mass equal to the absolute value of the negative heat difference divided by the specific latent heat of fusion of ice, see F(i) and G(i) in figure 4. The use of any of the phase change temperatures (e.g. 0℃or 100℃for water, the mixture has water as the liquid with the least phase change temperatures) as ta eliminates a recourse to fresh calculation as is the case with any other method. | Figure 4. Solutions of sample questions by heat content with assumed appropriate transition temperature Sample questions |
4. Conclusions
The three procedures viz the one body heat gainer or loser method, the heat content method (with its variants) and pair mixing, have been applied in solving common examples and the same answer obtained shows that the new methods are faultless and of general application. The versatility of the two new methods is shown by their use in solving sample questions. Solution B(i) of figure 1 and D(i) of figure 3 prove that difference in temperature determines the direction of heat flow. It is recommended that the various formulas be incorporated in the teaching and learning of this aspect of heat study.
References
| [1] | Bahl, B.S, A Bahl and G.D. Tuli, Essentials of Physical Chemistry. S. Chand and company Ltd. Ram Naga, New Delhi-110055, India, 2005, p238. |
| [2] | Anyakoha, M.W, New School Physics for Senior Secondary School, 3rd edition, African First Publishers, Onitsha Nigeria, 2010, pp 36, 202. |
| [3] | Nelkon, M, and Parker, P. Advanced Level Physics. Heinemann educational Books Ltd, London, 1970, p193. |
| [4] | Ezebuiro, G.N. Comprehensive Physics for Senior Secondary Schools, A Johnson Publishers Ltd, Surulere, Lagos Nigeria, 2004, p105. |
| [5] | Manacheril, G.T. Countdown to Senior Secondary School certificate Examination, Physics (A preparatory Course). Evans Brothers (Nigeria Publishers) Ltd, Jericho Road, Ibadan, Nigeria, 1991, p94. |

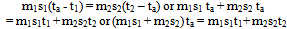
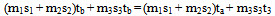
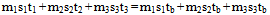
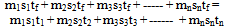


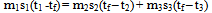
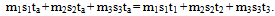




 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML