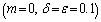-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2012; 2(4): 91-95
doi: 10.5923/j.ijtmp.20120204.06
On Thermal Stability Analysis for a Reacting Slab
Bakari Hamza 1, Estomih S. Massawe 1, Charles W. Mahera 1, Oluwole D. Makinde 2
1Mathematics Department, University of Dar es Salaam, P. O. Box 35062, Tanzania
2Faculty of Engineering, Cape Peninsula University of Technology, P. O. Box 1906, Bellville 7535, South Africa
Correspondence to: Estomih S. Massawe , Mathematics Department, University of Dar es Salaam, P. O. Box 35062, Tanzania.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this chapter, thermal stability analysis of the steady state exothermic chemical reaction in a slab of combustible material is investigated in the present of convective heat loss to the ambient. The nonlinear differential equations governing the system are obtained and solved using perturbation technique together with a special type of Hermite-Padé series summation and improvement method. The effects of various embedded parameters on the temperature profile and thermal stability of the system are presented graphically and discussed quantitatively. The possibility of thermal runaway phenomena was shown and the corresponding thermal criticality values were obtained and illustrated on a bifurcation diagram. The results reveal the thermal stability criticality as well as the effects of various embedded parameters on the system.
Keywords: Thermal Stability, Reacting Slab, Hermite-PadÉ Approximation
Article Outline
1. Introduction
- The study of thermal decomposition of reactive material in a slab is paramount in understanding the heat transfer of engineering processes. It is well known that thermal decomposition of different materials is dependent on size, shape and surface or environmental temperature as well as the physical properties of the material and environment. In other words for any given geometry, there is a critical size and surface temperature above which the heat generation inside the solid exceeds the heat dissipation to the surroundings[1].Theoretical study of transient heating in a slab of combustible material due to exothermic chemical reaction plays a significant role in many industrial applications[1]. These include: heavy oil recovery, storage of cellulosic materials, the pyrolysis of biomass and coal, the combustion of solids, waste incineration, coal gasification, etc. Without adequate knowledge of a reacting system, exothermic chemical process can accelerate significantly leading to runaway reaction, possible explosion, economical losses and cause emission of carbon dioxide and of toxic gases, like carbon monoxide through incomplete combustion ([2],[3],[4]).[5] presented a comprehensive review of chemical kinetic models for the heating-up of combustible materials. Meanwhile, analytical solutions of the highly nonlinear partial differential equations governing transient heating in a slab of combustible material due to exothermic reactions are usually impossible or extremely difficult to obtain. Hence in most cases, a numerical solution approach is adopted([6],[7],[8],[9],[10],[1])There are serious challenges of dangerous reactive material which justify the analysis of thermal decomposition of reactive material in a slab. Because many facilities and systems have chemically reactive materials that may have serious consequences if they are not handled, used and stored properly. Previous studies of the thermal decomposition of reactive material dealt with different dimensional shapes like cylindrical, rectangular parallelepiped, sphere, etc. The model to be introduced in this study is based on studies of[2] and[3].[2] studied the dynamics of hollow material and investigated the problem of strong exothermic explosions in cylindrical pipe, for putting large activation energy and concluded that the procedure reveals accurately the steady thermal criticality condition.[3] studied hydrodynamics and investigated the effect of variable viscosity in a thermal decomposable generalized Newtonian fluid subjected to unsteady one dimension shear flow in which the result were presented for some parameters in the problem. It was observed that increasing the non-Newtonian nature of the fluid helps to delay the onset of thermal runaway when compared to Newtonian nature of the fluid.[4] studied the thermal decomposition in a slab and found that time-independent solutions for the spatial structure of temperature, considering a slab with isothermal boundaries subjected to exothermic reaction and uniform plastic heating.Understanding the heat transfer and thermal stability characteristics of a reacting slab of combustive materials is extremely important in order to ensure the safety of its storage, handling and transportation([5,6]). Moreover, the phenomena of spontaneous ignition due to exothermic chemical kinetics in bulk solids such as coal, grain, hay, wool, etc., can be theoretically described by thermal combustion theory developed by[7,8]. One of the most important advantages of theoretical methods is that they can be applied as soon as a kinetic model had been evaluated from data from laboratory scale kinetic experiments. In particular, they allow estimation of runaway parameters in the earliest stages of the life cycle of a reactive material, thus ensuring elimination or significant reduction of the necessity for explosive experiments([9,10]).In this present study, we investigate the heat transfer and thermal stability characteristics of a reacting slab of combustible material in the presence of heat loss, neglecting the reactant consumption. The associated nonlinear differential equation modelling the problem is tackled analytically using perturbation method together with a special type of Hermite-Padé series summation and improvement method ([11,12]). Pertinent results are presented graphically and discussed.
2. Mathematical Model
- Consider the steady-state of an exothermic chemical reaction in a slab of combustible material with possibility ofheat loss to the surrounding ambient.
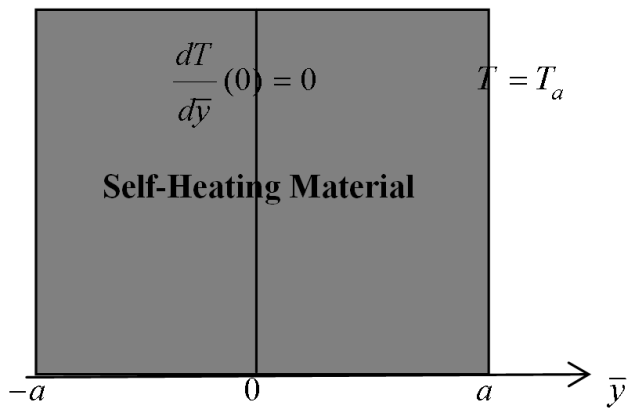 | Figure 1. Geometry of the Problem |
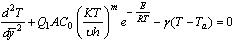 | , (1) |
 | (2) |
 is the absolute temperature,
is the absolute temperature, is the ambient temperature,
is the ambient temperature,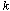 is the thermal conductivity of the material,
is the thermal conductivity of the material,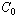 is the reactant concentration,
is the reactant concentration,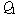 is the exothermicity,
is the exothermicity,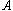 is the rate constant,
is the rate constant,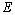 is the activation energy,
is the activation energy,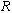 is the universal gas constant,
is the universal gas constant,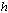 is the Planck’s number,
is the Planck’s number,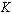 is the Boltzmann’s constant,
is the Boltzmann’s constant,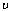 is the vibration frequency,
is the vibration frequency,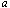 is the slab half width,
is the slab half width, 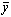 is the distance measured transverse direction,
is the distance measured transverse direction,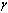 is the heat loss parameter,
is the heat loss parameter,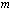 is the numerical exponent such that
is the numerical exponent such that 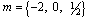 represent numerical exponent for sensitized, Arrhenius and Bimolecular kinetics respectively.We introduce the following dimensionless variables into equations.(1)-(2);
represent numerical exponent for sensitized, Arrhenius and Bimolecular kinetics respectively.We introduce the following dimensionless variables into equations.(1)-(2); 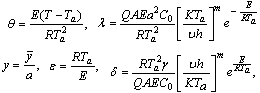 | (3) |
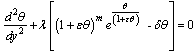 | (4) |
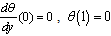 | (5) |
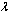 is the Frank-Kameneskii parameter,
is the Frank-Kameneskii parameter,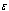 the activation energy parameter,
the activation energy parameter,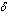 the heat loss parameter.The thermal decomposition and stability of the reacting combustible material depend on the parameters in equation.(4), which are of great importance with respect to applications in the area of industrial safety and handling techniques of explosives.
the heat loss parameter.The thermal decomposition and stability of the reacting combustible material depend on the parameters in equation.(4), which are of great importance with respect to applications in the area of industrial safety and handling techniques of explosives.3. Perturbation Method
- Due to the nonlinearity nature of the temperature variable in equations(4)-(5), it is convenient to seek a solution in the form of a power series expansion in parameter
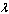 , i.e.
, i.e.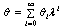 | (6) |
 , we obtained the followings:Order zero
, we obtained the followings:Order zero 
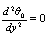 | (7) |
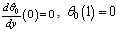 | (8) |
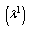
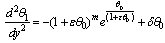 | (9) |
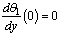 | (10) |
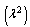
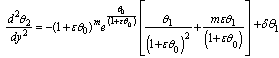 | (11) |
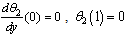 | (12) |
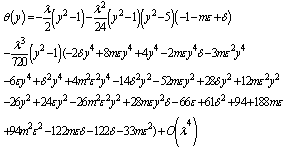 | (13) |
 . However, using Hermite-Padé series summation and improvement technique, we have extended the usability of the solution series beyond small parameter values as illustrated in the following section.
. However, using Hermite-Padé series summation and improvement technique, we have extended the usability of the solution series beyond small parameter values as illustrated in the following section.4. Thermal Stability Analysis
- From the application point of view, it is very important to determine the appearance of criticality or non-existence of steady-state solution for certain parameter values. In order to achieve this, a special type of Hermite-Padé series summation and improvement method will be utilized([11,12]). Let
 | (14) |
 along the slab centreline can be written as
along the slab centreline can be written as 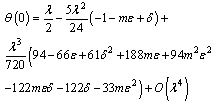 | (15) |
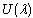 is a local representation of an algebraic function of
is a local representation of an algebraic function of 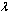 in the context of nonlinear problems. We seek an expression of the form
in the context of nonlinear problems. We seek an expression of the form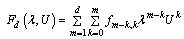 | (16) |
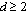 , such that
, such that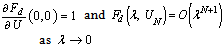 | (17) |
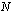 linear equations for the unknown coefficients of
linear equations for the unknown coefficients of 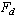 . The entries of the corresponding matrix depend only on the
. The entries of the corresponding matrix depend only on the 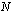 given coefficients
given coefficients 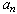 and we shall take
and we shall take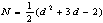 , so that the number of equations equals the number of unknowns. The polynomial
, so that the number of equations equals the number of unknowns. The polynomial 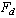 is a special type of Hermite-Padé approximant and is then investigated for bifurcation and criticality conditions using Newton diagram([13]).
is a special type of Hermite-Padé approximant and is then investigated for bifurcation and criticality conditions using Newton diagram([13]).5. Results and Discussion
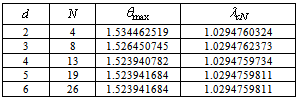
- In this section, we validate the above theoretical results using physically realistic values of various embedded parameters in the numerical experiment. We note that increasing parameter value of λ indicates an increase in the rate of exothermic chemical kinetics in the slab. In order to obtain the thermal stability criterion in the reacting slab, the Hermite-Padé approximation procedure in section(4) above was applied to the first few terms of the solution series in section(3) and we obtained the results as shown in tables(1) and(2) below:The results in table(1) reveal the rapid convergence of Hermite-Padé series summation and improvement procedure with gradual increase in the number of series coefficients utilized in the approximants for the thermal criticality condition. In table (2), it is noteworthy that the magnitude of thermal explosion criticality
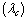 increases with an increase in the parameter values of
increases with an increase in the parameter values of 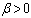 due to an increase in the heat loss to the surrounding ambient. This invariably will lead to a delay in the development of thermal runaway in the reacting slab. Since the heat is not accumulated in the slab, it enhances the thermal stability of the system. Similar effect of thermal stability enhancement is observed with increasing values of activation energy parameter
due to an increase in the heat loss to the surrounding ambient. This invariably will lead to a delay in the development of thermal runaway in the reacting slab. Since the heat is not accumulated in the slab, it enhances the thermal stability of the system. Similar effect of thermal stability enhancement is observed with increasing values of activation energy parameter 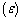 . Increasing values of
. Increasing values of 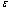 implies that the activation energy of the reacting slab is very low; hence the volatility tendency of the reacting slab is greatly reduced. Furthermore, it is interesting to note from table(2) that thermal explosion occur faster in a bimolecular
implies that the activation energy of the reacting slab is very low; hence the volatility tendency of the reacting slab is greatly reduced. Furthermore, it is interesting to note from table(2) that thermal explosion occur faster in a bimolecular 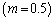 type of exothermic reaction as compared to the Arrhenius
type of exothermic reaction as compared to the Arrhenius 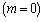 and sensitised
and sensitised 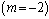 type of reaction. A slice of the bifurcation diagram for
type of reaction. A slice of the bifurcation diagram for 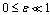 in the
in the 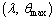 plane is shown in figure.(2). It represents the qualitative change in the thermal system as the parameter
plane is shown in figure.(2). It represents the qualitative change in the thermal system as the parameter 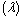 increases. In particular, for
increases. In particular, for 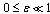 and
and 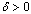 there is a critical value
there is a critical value 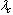 (a turning point) such that, for
(a turning point) such that, for 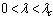 there are two solutions(labelled I and II). The upper and lower solution branches occur due to the nonlinearity in the energy balance equation. When
there are two solutions(labelled I and II). The upper and lower solution branches occur due to the nonlinearity in the energy balance equation. When 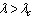 the system has no real solution and displays a classical form indicating thermal runaway. As exothermic reaction due chemical kinetics increases, the slab temperature increases uncontrollably until it ignites.
the system has no real solution and displays a classical form indicating thermal runaway. As exothermic reaction due chemical kinetics increases, the slab temperature increases uncontrollably until it ignites.
|
|
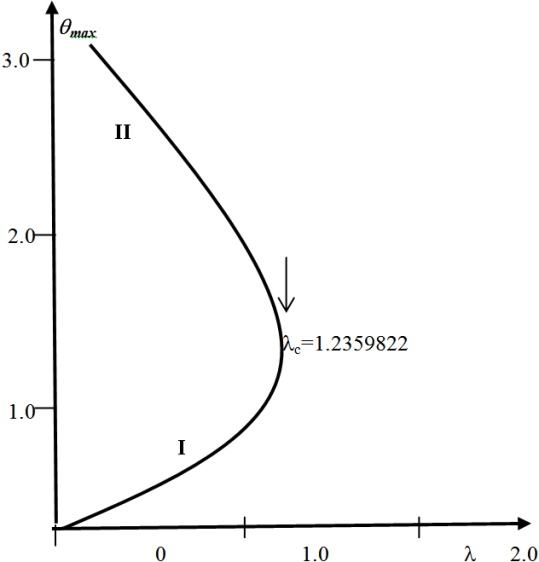 | Figure 2. A Slice of Approximate Bifurcation Diagram in the 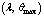 Plane When Plane When 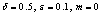 |
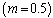 and lowest for sensitized reaction
and lowest for sensitized reaction 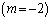 , hence confirming the earlier results in the literature. This observation is also in agreement with the results highlighted in table(2). In figure(4) we observe that the slab temperature decreases with an increase in the heat loss parameter
, hence confirming the earlier results in the literature. This observation is also in agreement with the results highlighted in table(2). In figure(4) we observe that the slab temperature decreases with an increase in the heat loss parameter 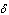 . The decrease in the slab temperature with increasing
. The decrease in the slab temperature with increasing 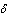 can be attributed to the cooling action of heat loss on the slab. Figure(5) show that the slab temperature increases with an increase in the parameter values of
can be attributed to the cooling action of heat loss on the slab. Figure(5) show that the slab temperature increases with an increase in the parameter values of 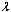 . As the Frank-Kamenetskii parameter
. As the Frank-Kamenetskii parameter 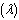 increases, the slab internal heat generation due to exothermic reaction increases, this invariably leads to an elevation in the slab temperature.
increases, the slab internal heat generation due to exothermic reaction increases, this invariably leads to an elevation in the slab temperature.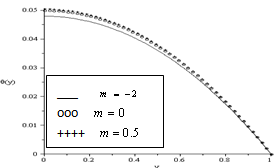 | Figure 3. Effect of Reaction Type Index on Temperature Profiles  |
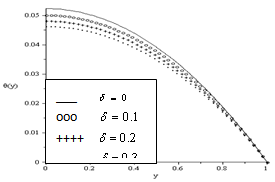 | Figure 4. Effect of Heat Loss on Slab Temperature Profiles for  |
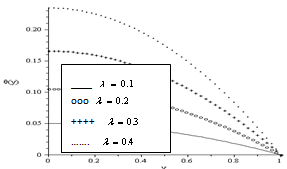 | Figure 5. Effect of Increase in Exothermic Reaction Rate on the Slab Temperature Profiles for  |
6. Conclusions
- The steady state exothermic chemical reaction in a slab of combustible material is considered. The nonlinear ordinary differential equation governing the problem was formulated and solved analytically using the perturbation technique together with a special type of the Hermite-Padé series summation and improvement method. The possibility of thermal runaway phenomena was shown and the corresponding thermal criticality values were obtained and illustrated on a bifurcation diagram. An increase in the parameter value of λ indicates increasing rate of exothermic chemical kinetics. As parameter δ increases in value (δ>0), the rate of heat loss to the ambient increases as well as the thermal explosion criticality values. This invariably enhances the thermal stability of the reacting slab by preventing the occurrence of thermal runaway.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML