1. Introduction

Before passing to the analysis of the conservation laws for the gas-dynamic system under consideration, it should be told a little of the concept of 'conservation laws'.

Owing to the development of science the concept of 'conservation laws' has assumed a different meaning in various branches of physics and mechanics.

In areas of physics related to the field theory and in the theoretical mechanics 'the conservation laws' are those according to which there exist conserved physical quantities or objects. These are the conservation laws that above were named 'exact'. Such conservation laws are described be the closed exterior skew-symmetric forms[1]. (It is known that the differential of closed exterior form equals zero, that is, the closed form is a conserved quantity).

In mechanics and physics of continuous media the concept of 'conservation laws' relates to the conservation laws for energy, linear momentum, angular momentum, and mass that establish the balance between the change of physical quantities and external action. These conservation laws can be named the balance conservation laws. They are described by differential (or integral) equations. It may be pointed that all continuous media such as thermodynamic, gas dynamical, cosmic systems and others (which can be referred to as material systems), are subject to the balance conservation laws.

The analysis of the equations of balance conservation laws carried out using the skew-symmetric differential forms showed that the balance and exact conservation laws are related to each other. The conserved physical quantities or objects, whose availability points out to that the exact conservation laws obey, are obtained from the equationsdescribing the balance conservation laws. The process of passing from the balance conservation laws to exact conservation laws is accompanied by the origination of a certain physical structures and the emergence in material (continuous) media of observed formations (fluctuations, turbulent pulsations, waves, massless particles and others)[2]. The processes of origination of the vorticity and turbulence are examples of such processes.

As the analysis of the equations of the balance conservation laws showed, these processes are the results of noncommutativity of the balance conservation laws.

2. Gas Dynamical System of Ideal Gas

First of all, we consider the simplest gas dynamical system, namely, a flow of ideal (inviscous, heat nonconductive) gas. In the second part of the paper the gas dynamic system of the viscous heat conductive gas will be considered.

2.1. The Equation of the Conservation Law. Evolutionary Relation

Assume that the gas is a thermodynamic system in the state of local equilibrium (whenever the gas dynamic system itself may be in nonequilibrium state), that is, the following relation is fulfilled [3]:

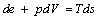(1)

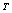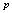Where, and 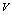are the temperature, the pressure and the gas volume, s, e are entropy and internal energy per unit volume. [Relation (1) determines the entropy s as a thermodynamical state function. For the gas dynamical system the thermodynamical state function describes only the state of the gas dynamical element (a gas particle). For the gas dynamical system the state function is also the entropy. But in this case the entropy is a function of space-time coordinate.]

Let us introduce two frames of reference: an inertial one that is not connected with the gas dynamical system and an accompanying frame of reference that is connected with the manifold formed by the trajectories of the system elements. (Both Euler's and Lagrange's systems of coordinates can be examples of such frames[4]).

In the inertial frame of reference the Euler equations are the conservation laws for energy, linear momentum and mass of ideal gas[4].

The equation of the conservation law of energy for ideal gas can be written as

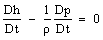(2)

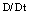where is the total derivative with respect to time. Here 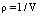and h are respectively the density and enthalpy of the gas.

Expressing enthalpy in terms of internal energy e with the help of formula 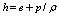and using relation (1), the balance conservation law equation can be put to the form

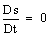(3)

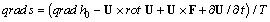And respectively, the equation of the conservation law linear momentum can be presented as [4, 5]

(4)

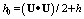Here U is the velocity of the gas particle, , F is the mass force ( in this equation is defined only in the plane normal to the trajectory).[Here it was tolerated a certain incorrectness. Equations (3) and (4) are written in different forms. However, this incorrectness will not effect on results of the qualitative analysis of the evolutionary relation obtained from these equations.]

Since the total derivative with respect to time is that along the trajectory, in the accompanying frame of reference the equation of the conservation law for energy takes the form: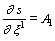

(5)

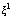Here is the coordinate along the trajectory, .

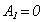In the accompanying frame of reference the equation of conservation law for linear momentum can be presented as

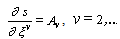(6)

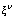where is the coordinate in the direction normal to the trajectory, 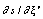is the left-hand side of equation (4), and 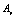is obtained from the right-hand side of equation (4).

Equations (5) and (6) can be convoluted into the relation

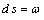(7)

where

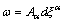is the first degree differential form (here ).

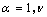Since the equations of conservation law are evolutionary ones, the relation obtained is also an evolutionary relation.

2.2. Analysis of the Evolutionary Relation. Nonidentity of the Evolutionary Relation

The evolutionary relation (7) is a nonidentical one as it involves the unclosed differential form.

While describing actual processes, the evolutionary form 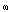is not closed. The differential of evolutionary form 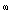and its commutator are nonzero. The differential of evolutionary form

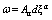is expressed as

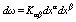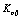where are the components of the form commutator.

The commutator of differential form 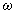is nonzero. Without accounting for terms that are connected with the deformation of the manifold formed by the trajectories, the commutator can be written as

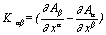The coefficients 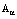of the form 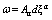have been obtained either from the equation of the balance conservation law for energy or from that for linear momentum. This means that in the first case the coefficients depend on the energetic action and in the second case they depend on the force action. In actual processes energetic and force actions have different nature and appear to be inconsistent. The commutator of the form 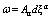constructed of the derivatives of such coefficients is nonzero.

This means that the differential of the form 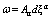is nonzero as well. Thus, the form 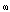proves to be unclosed and is not a differential. In the left-hand side of relation (7) it stands a differential, whereas in the right-hand side it stands an unclosed form that is not a differential.

Such a relation cannot be an identical one.

The nonidentity of the evolutionary relation means that the balance conservation law equations are inconsistent. And this indicates that the balance conservation laws are noncommutative. (If the conservation laws be commutative, the equations would be consistent and the evolutionary relation would be identical).

The evolutionary relation obtained from the balance conservation laws reflects the character of interactions of the balance conservation laws. The nonidentity of the evolutionary relation means that the balance conservation laws are noncommutative, that is, the results of action of the conservation laws depend on the order in what they act.

{It should be noted that for all material systems (such as thermodynamic, gas dynamical, cosmic and others) the evolutionary relation obtained from the equations of balance conservation laws is nonidentical, and this points to the noncommutativity of balance conservation laws.

The 'noncommutativity' of the balance conservation laws can be explained in the following manner.

Suppose that firstly the energetic and then the force perturbations act onto a local domain of the material system (an element and its neighborhood). Let the local domain be in some state A in the initial instant. According to the balance conservation law for energy, under exposure to the energetic perturbation the local domain develops from the state A into the state B. Then, according to the balance conservation law for momentum, under exposure to the force perturbation it develops from the state B to the state C. Suppose now that the sequence of the actions is changed, namely, firstly the force perturbation and then the energetic one act, and the system develops firstly into any state B` and then it proceeds into the state C`. If the state C` coincides with the state C (this corresponds to the local equilibrium state of the system), that is, the result does not depend on the sequence of perturbations of different types (and on the sequence of implementing the relevant balance conservation laws), then this means that the balance conservation laws are commutative. If the state C` does not coincide with the state C (that is, the system state turns out to be not the equilibrium one), this means that the balance conservation laws prove to be noncommutative.

The reason for noncommutativity of the balance conservation laws is connected with the fact that the material system is subject to actions of different nature, the nature of these actions is inconsistent with the nature of the material system.}

Thus, if we even doesn't know the specific expression of the form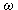, one can state that, due to inconsistence of external actions, the evolutionary relation turns out to be nonidentical one for real processes, and this points out to the noncommutativity of balance conservation laws.

To what results the noncommutativity of balance conservation laws leads?

2.3. Nonequilibrium of the Gas Dynamical System

The further analysis of the evolutionary relation allows to disclose the effect of noncommutativity of the balance conservation laws on the evolutionary processes in gas dynamical system that lead to development of instability and origination of vorticity.

The role of the evolutionary relation in evolutionary process is due to the fact that this relation includes the differential of entropy 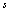, which specifies the state of gas dynamical system.

However, here there is a subtle point. One can obtain the differential of entropy 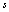from the evolutionary relation only if this relation proves to be identical. When the relation (7) appears to be identical one (if the form 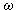be a closed form, and hence it is a differential), one can obtain the differential of entropy 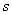and find entropy as a function of space-time coordinates. It is precisely the entropy that will be the gas dynamic function of state. The availability of the gas dynamic function of state would point to the equilibrium state of gas dynamic system. If relation (7) be not identical, from this relation the differential of entropy 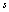cannot be defined. This will point to an absence of the gas dynamic function of state and nonequilibrium state of the system.

{It should be noted once more that in the relation (1), which describes the thermodynamic system state, the dependence of entropy on thermodynamical variables is considered, whereas in the evolutionary relation forgas-dynamic system the dependence of entropy on space-time coordinates is analyzed. The entropy, which depends on thermodynamic variables, is a state function of thermodynamic system, and the entropy, which depends on space-time coordinates, is a state function of gas dynamic system. In the gas dynamic system the entropy as a thermodynamic function specifies the state of gas rather then of the gas dynamic system.}

It has been shown above that, since the evolutionary relation is not identical because of the noncommutativity the conservation laws, from this relation one cannot get the state differential 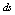that may point out to the equilibrium state of the gas dynamical system. This means that the gas dynamical system state is nonequilibrium.

The nonequilibrium is produced by internal forces that are described by the commutator of the form 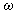. (If the evolutionary form commutator be zero, the evolutionary relation would be identical, and this would point out to the equilibrium state, i.e. the absence of internal forces.) Everything that gives the contribution into the evolutionary form commutator leads to emergence of the internal force that causes the nonequilibrium state and leads to development of instability.

It becomes evident that a cause of the gas dynamic nonequilibrium and instability is something that contributes into the commutator of the form .

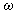From the analysis of the coefficients 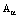(see the right-hand side of equation (4) and with taking into account that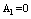, one can see that the terms related to the multiple connectedness of the flow domain (the second term in (4)), the nonpotentiality of the external forces (the third term in (4)) and the nonstationarity of the flow (the forth term in (4)) contribute to the commutator. All these factors lead to the emergence of internal forces, the nonequilibrium state and the development of instability.

One can see that the development of instability is caused by the not simple connectedness of the flow domain, the nonpotential external (for each local domain of the gas dynamic system) forces and the nonstationarity of the flow. (In the common case, the thermodynamic, chemical, oscillatory, rotational and translational nonequilibrium will effect on the gas dynamic instability).

All these factors lead to emergence of internal forces, that is, to nonequilibrium and to development of various types of instability. (It may be noted that, for the case of ideal gas, Lagrange derived the condition of the eddy-free stable flow.

This condition is as follows: the domain must be simple connected one, forces must be potential and the flow must be stationary. One can see, that under fulfillment of these conditions there are no terms that contribute into the commutator).

And yet, for every type of instability one can find an appropriate term giving contribution into the evolutionary form commutator, which is responsible for this type of instability.

Thus, there is the unambiguous connection between the type of instability and the terms that contribute into the evolutionary form commutator in the evolutionary relation. {In the general case one has to consider the evolutionary relations that correspond to the balance conservation laws for angular momentum and mass as well}.

Hence one can see that the noncommutativity of the balance conservation laws leads to emergence of internal forces (whose value is described by the evolutionary form commutator) and to appearance of the nonequilibrium.

The nonidentical evolutionary relation is selfvarying one. (Since one of the objects is an unmeasurable quantity, the other cannot be compared with the first one, and hence, the process of mutual variation cannot stop.)

Such selfvarying of evolutionary relation points to the fact that the gas dynamic system state changes. However, in this case the gas dynamic system state remains nonequilibrium because the nonidentity of evolutionary relation holds.

Whether the gas dynamic system can get rid of the internal force and transit into the equilibrium state?

2.4. Transition of the Gas Dynamic System into a Locally Equilibrium State. Origination of Physical Structures

It turns out that the gas dynamic system can transit into the locally equilibrium state.

From the properties of nonidentical relation it follows that under selfvariation of nonidentical relation it can proceed the degenerate transformation when from the unclosed evolutionary form the skew-symmetric differential form closed on some structure (pseudostructure) can be obtained and the identical relation can be obtained from nonidentical relation. The degrees of freedom of gas dynamic systems (translational, rotating, oscillating and others) are the conditions of degenerate transformation. The conditions of degenerate transformation specify the pseudostructures: characteristics, singular points, envelopes of characteristics and so on. The realization of the conditions of degenerate transformation leads to the realization of pseudostructure 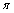(the closed dual form) and formatting the closed inexact form

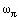whose closure conditions have the form

,

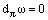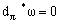On the pseudostructure 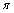from evolutionary relation (7) it is obtained the identical relation

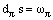(8)

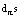from which the differential can be obtained. This means that there exists the state function of gas dynamic system, namely, the entropy whose availability points to the locally-equilibrium state of the gas dynamic system. (In the papers on gas dynamics it is assumed that from equation (5) one can obtain the entropy along the trajectory. However, it occurs that entropy as a function of space-time coordinates cannot exist if the conditions of degenerate transformations are not satisfied. Entropy as a function of the state has to be satisfied both to equation (5) and equation (6).

Realization of pseudostructure 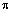and formatting the closed inexact form 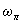points to emergence of physical structure, i.e. a certain conserved object. The characteristics, the singular points, the envelopes of characteristics and so on(pseudostructures - the closed dual forms) with conserved quantities (closed inexact form) are examples of such physical structures.

One can see that the identical relation (8) holds the duality. The left-hand side of this relation includes the differential 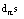, which specifies gas dynamic system and whose availability points to the locally-equilibrium state of gas dynamic system. And the right-hand side includes a closed inexact form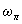, which is a characteristics of physical structures.

This shows that the transition of gas dynamic system into the locally equilibrium state (under realization of degrees of freedom) is accompanied by the origination of physical structures.

The origination of physical structure reveals as a new measurable and observable formation that spontaneously arises in gas dynamic system.

In gas dynamical system of ideal gas formations that correspond to emerged physical structures are waves, shock waves, vortices.

(In gas dynamical system of viscous gas, formations that correspond to emerged physical structures are turbulent pulsations).

Since the created formation is a result of transition of an unmeasurable quantity described by the evolutionary form commutator into a measurable physical quantity, it is evident that the intensity of the formation created is controlled by the quantity that was stored by the evolutionary form commutator.

One can see that in gas dynamical system, even in the case of ideal gas, it can originate the physical structures and relevant formations that lead to emergence of vorticity.

It should be emphasized once more that the origination of various structures only proceeds under realization of the conditions of degenerate transformations that are conditioned by the degrees of freedom such as translational, rotating, oscillating and others.

The conditions of degenerate transformations are realized as vanishing some functional expressions such as determinants, Jacobians of transformations, etc. These conditions specify the integral surfaces (pseudostructures): the characteristics (the determinant of coefficients at the normal derivatives vanishes), the singular points (Jacobian is equal to zero), the envelopes of characteristics of the Euler equations and so on. Under passing throughout the integral surfaces the gas dynamic functions or their derivatives suffer shocks (contact shocks). Below we present the expressions for calculation of such shocks of derivatives in the direction normal to characteristics (and to trajectories).

The degenerate transformation is realized as a transition from the accompanying noninertial frame of reference to the locally inertial frame of reference, that is, the transition one frame of reference to another nonequivalent frame of reference. The evolutionary form and nonidentical evolutionary relation are defined in the noninertial frame of reference (deforming manifold). But the closed exterior form and the identical relation are obtained with respect to the locally-inertial frame of reference (pseudostructure).

Let as analyze which types of instability and what gas dynamic formations can originate under given external action.

1). Shock, break of diaphragm and others. The instability originates because of nonstationarity. The last term in (4) gives a contribution into the commutator. In the case of ideal gas whose flow is described by equations of the hyperbolic type the transition to the locally equilibrium state is possible on the characteristics and their envelopes. The corresponding formations are weak and shock waves.

2). Flow of ideal (inviscous, heat nonconductive) gas around bodies. Action of nonpotential forces. The instability develops because of the multiple connectedness of the flow domain and a nonpotentiality of the body forces. The contribution into the commutator comes from the second and third terms in (4). Since the gas is ideal one and 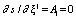, that is, there is no contribution into the each fluid particle, the instability of convective type develops. For 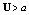(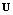is the velocity of the gas particle, 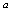is the speed of sound) the set of equations of the balance conservation laws belongs to the hyperbolic type, and hence the transition to the locally equilibrium state is possible on the characteristics and on the envelopes of characteristics as well, and weak and shock waves are formations of the system. If 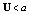when the equations are of elliptic type, such a transition is possible only at singular points. The formations emerged due to the convection are of vortex type. At long acting the large-scale structures can be produced.

Studying the instability on the basis of the analysis of entropy behavior was carried out in the works by Prigogine and co-authors [6, 7]. In that works the entropy was considered as the thermodynamic function of state (though its behavior along the trajectory was analyzed). By means of such state function one can trace the development (in gas fluxes) of the thermodynamic instability only [7]. To investigate the gas dynamic instability it is necessary to consider entropy as the gas dynamic state function, i.e. as a function of the space-time coordinates. Whereas for studying the thermodynamic instability one has to analyze the commutator constructed by the mixed derivatives of entropy with respect to the thermodynamic variables, for studying the gas dynamic instability it is necessary to analyze the commutators constructed by the mixed derivatives of entropy with respect to the space-time coordinates.

3. Gas Dynamical System of Viscous Gas

In the case of ideal gas the expression 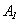in the equation of energy (see equations (5)) is equal to zero. In the case of the viscous heat-conductive gas the expression 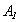will depend on the viscosity and the heat-conductivity.

3.1. The Equation of the Conservation Law of Energy for Viscous Gas

The expression 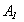of the equation of energy of the viscous heat-conductive gas described in the inertial frame of reference by a set of the Navier-Stokes equations can be written as [4]

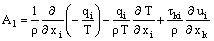(9)

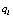Here is the heat flux, 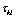is the viscous stress tensor.

In the case of viscous gas the terms connected with the transport phenomena (viscous and heat-conductive) will contribute into the evolutionary form commutator. This term is responsible for emergence of turbulent pulsations.

In the general case, the expression 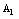will include the terms accounting for the chemical, oscillatory, rotational, translational and other effects [4] that will contribute into the evolutionary form commutator and influence on the development of instability.

Let as analyze the following example.

3.2. Boundary Layer

The instability originates due to the multiple connectness of the domain and the transport phenomena (the effect of viscosity and thermal conductivity). Contributions into the commutator produce the second term in (4) and the second and third terms in expression (9). The transition to the locally equilibrium state is allowed at singular points because in this case 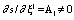, that is, the external exposure acts onto the gas particle separately, the development of instability and the transitions to the locally equilibrium state are allowed only in the individual fluid particle. Hence, the formations emerged behave as pulsations. These are turbulent pulsations.

It is commonly believed that the instability is an emergence of any structures in the gas dynamic flow. From this viewpoint the laminar boundary layer is regarded as stable one, whereas the turbulent layer regarded as unstable layer. However the laminar boundary layer cannot be regarded as a stable one because of the fact that due to the not simple connectedness of the flow domain and the transport processes the instability already develops although any formations do not originate. In the turbulent boundary layer the emergence of pulsations is a transition to the locally equilibrium state, and the pulsations themselves are local formations. The other matter, due to the global nonequilibrium the locally equilibrium state is broken up and the pulsations weaken.

4. Modeling Instable Flows

It should be said a little about modelling instable flows.

As it is known, some authors tried to account for the development of instability by means of improving the equations modelling the balance conservation laws (for example,

by introducing the high-order moments) or by introducing additional equations. However, such attempts give no satisfactory results. To describe the nonequilibrium flow and the emergence of the gas dynamic structures (waves, vortices, turbulent pulsations) one must add the evolutionary relation obtained from the balance conservation law equations to the balance conservation law equations. Under numerical modelling the gas flows one has to trace for the transition from the evolutionary nonidentical relation to the identical relation (for the transition from an evolutionary unclosed form to an exterior closed form), and this will point to the emergence of a certain physical structure.

Below we present an example of calculating the breaks of derivatives of the gas dynamic functions that are necessary for numerical analysis of gas dynamic flows.

4.1. Breaks of Normal Derivatives on Characteristics and Trajectories

While studying the effects connected with the origination of the vorticity one can notice a certain specifics of numerical solving the Euler equations[4]. This may be demonstrated by the following example. Assume, that the initial conditions correspond to the isentropic flow, that is, entropy is the same along all trajectories. For ideal gas under consideration the entropy conserves along the trajectory. From this it follows that entropy has to conserve during all time of flow. However, in actual cases (unsteady flow, flow along the body, heterogeneous medium) the derivative of entropy along the direction normal to trajectory suffers the break. Thus we have that, from one side, entropy (function) must be constant and, from other hand, its derivatives suffer the breaks. This contradiction is resolved with taking into account the fact that the break of derivative is compensated by changing the stream function or bending the trajectory. It is this effect that must be accounted for in the process of numerical calculation. In particular, when calculating the one-dimensional nonstationary nonisentropic flow of gas, the conditions on the characteristics includes the derivative of entropy with respect to the coordinate normal to trajectory (in space of two variables, namely, time and coordinate). To calculate this derivative one must know the break of derivative of entropy. This can be obtained from the relations that connects the breaks of derivatives of the gas dynamic functions.

These relations are found from the dynamic conditions of the consistency of the Euler equations. In paper[8] the dynamical conditions of consistency of the Euler equations for the case 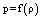were considered.

In the present work by a similar manner it is analyzed the case when 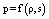, where s is the entropy, and the relations that connect the breaks of derivatives of the functions describing the particle velocity, the sound speed, and entropy are obtained. These relations enable one to carry out numerical calculations of the nonisentropic gas flows.

The scheme of obtaining these relations for one- dimensional nonstationary equations is the following. At the beginning, the Euler equations are written down. Then the equations for characteristics and the conditions on characteristics are derived. The kinematic conditions of consistency[8], which mutually connect the breaks of derivatives of the gas dynamic functions, are written down. These conditions are substituted into the Euler equations. As a result, the homogeneous set of equations for the breaks of derivatives of the functions desired is obtained. On the characteristic surface the determinant of this set equals zero, and from this it is found the nontrivial solution for the breaks of derivatives of the functions desired in their dependence on a value of one of others.

If to take 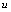(the gas velocity), (the sound speed), and s, the following relations are obtained[9]:

1) In the direction normal to the trajectory the derivatives of the sound speed and entropy suffer breaks (the derivative of velocity does not suffer a break). These breaks are connected between them by the relation:

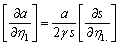where 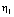is the direction normal to the trajectory, 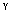is the Poisson constant.

2) In the direction normal to the characteristics the derivatives of the as velocity and the speed of sound suffer breaks (the derivative of ntropy does not suffer break). These breaks are connected between them y the relation:

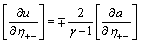where 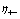are the directions normal to the corresponding characteristics.

5. Conclusions

It has been shown that the conservation laws of energy and linear momentum turn out to be noncommutative. The noncommutativity of the conservation laws that leads to an emergence of internal forces and an appearance of the nonequilibrium is a cause of development of instability in gas-dynamic system that are accompanied by origination of vorticity and turbulence.

These investigation can be used in solving the gas dynamical problem and an interpretation of the results obtained.

It should be noten that these results it appeared possible to receive only by means of the skew-symmetric differential forms, which properties correspond to conservation laws. The skew-symmetric differential forms on deforming (nonintegrable) manifolds were used in addition to exterior forms, which have differentiable manifolds as a basis. Such skew-symmetric forms (whose existence was established by the author) are evolutionary ones and possess a nontraditional mathematical apparatus (such as nonidentical relations, degenerate transformations, the transition from nonintegrable manifold to integrable one, and others).

Use of such skew-symmetric forms allowed to open properties of the conservation laws and their role in evolutionary processes.