Zayko Y.N.
Stolypin’s Volga Regional Institute of Control, 410031, Saratov, Russia
Correspondence to: Zayko Y.N. , Stolypin’s Volga Regional Institute of Control, 410031, Saratov, Russia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This article presents dynamics of dual phase, which is connected with dual character of dions – hypothetical particles possessing both electrical and magnetic charges. For description of dual phase the set of equations is received from condition that Maxwell equations conserve their electrical character under dual transformations, what corresponds to effective electrical charge of dion. The mechanism of dual phase synchronization in different parts of space is revealed. It is shown, that solutions of Maxwell equations for spherical waves with zero orbital moment momentum correspond to monopole radiation of dion. Goldstone character of dual phase so as its geometrical character is shown. This article supplements previous investigations of G. Rainich[1] and J. Wheeler and C. Misner[2, 3]. Results of this article can explain many-years failures in searching magnetic charges (monopoles).
Keywords:
Dion, Magnetic Charge, Goldstone Mode
1. Introduction
Maxwell equations can be written in the form symmetric with respect to permutation of electrical and magnetic charges[4]: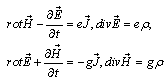 | (1) |
Here E and H – are electrical and magnetic fields, ρ and J – number of particles’ and flow of charge densities, correspondingly(in systems of Heavyside-Lorenz units). We suppose that particles called “dions” which play role of the sources of fields have both electrical (e) and magnetic charge (g). It is known that with the help of dual transformation of fields: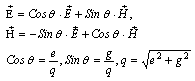 | (2) |
θ- is a parameter of dual transformation (dual phase), one can eliminate magnetic charge from the (1), and they will look as follows[1]: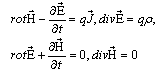 | (3) |
These equations describe electrodynamics of particleswhich have effective electrical charge q1. Thus, magnetic charge which is introduced in a such way became elusive[4]2. Value of parameter θ is considered as constant but undetermined one due to indeterminacy of values of е and g. From this point of view charges, both electrical and magnetic take their denominations in the result of agreement and we are free change this one and name electrical charge as magnetic and vice versa, so as for fields. Such metaphysical way of thinking is inappropriate in contemporary physics. On the other hand it is supposed in present article that some field is connected with phase θ, what imply definite restrictions on values of θ in neighbouring points of space and time. These restrictions have a form of equations which can be received from the Lagrangian (or from the equations) of electromagnetic fields in the assumption that θ – is independent dynamical variable. Some hypothetical mass-less particle can be connected with that field, which transfers interaction between dions[5], just like photons transfer interaction between electrically charged particles. Analogous problems were concerned earlier by G. Rainich[1], J. Wheeler and C. Misner[2, 3] for charged particles interacting with their own gravitational field and by L. Witten[6], who studied problem of initial conditions for Maxwell-Einstein equations. Despite great significance of that works some problems stayed unsolved, such as problem of dual phase synchronization what has been stressed by R. Penrose3.These reasons can be supplemented by arguments, which are analogous to ones that leads to the idea of dynamical nature of electrical charge and are formulated in terms of calibration fields, which are responsible for electromagnetic interaction[4, 7].
2. Basic Equations
Field equations are usually derived from Lagrangian, which is connected with corresponding fields. In problems of dual electrodynamics this approach leads to well-known difficulties[4]. Nonetheless, attempts like that are undertaking. For this one could take for example, a Lagrangian of type presented below for electromagnetic field, which is created by dually charged particles[4]: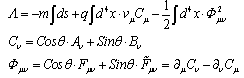 | (4) |
Aν – is a vector potential and, Bν – pseudo-vector one; Fμν – is a tensor of electromagnetic field; sign ~ (tilde) denotes tensor which is dual for Fμν; m – mass of dions, vμ – their velocity. Taking variation of Λ on potentials one can receive Maxwell equations for photons: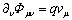 | (5) |
If one takes a derivative of (5) and considers θ as a function of co-ordinate and time he receives equations which describe dynamics of θ, which look as follows4: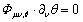 | (6) |
Comma means derivative on corresponding variable, ∂ν = ∂/∂xν.Equations (6) have nontrivial solutions if their determinant Δ = 0. Explicit calculation gives us: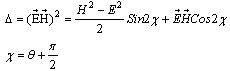 | (7) |
Thus, nontrivial dynamics of phase θ takes place if both invariants of electromagnetic field are equal zero: H2-E2=0 and EH=0. Let us consider some possible solutions of equations (6). Taking algebraic supplements for first two rows of Φμν,θ (θ) = Φμν (χ) one can receive two different systems of equations: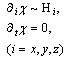 | (8a) |
and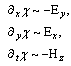 | (8b) |
If one chooses another rows (or columns) he receives the same results, which differ only with denomination of co-ordinate axes. Combination of equations (8) and (3) gives equations for χ: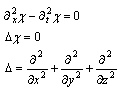 | (9) |
Co-ordinate axis x is standing out from others because it picks a direction of solution’s propagation as a wave with light speed c5. It is obvious that it is conditioned by external reasons and х- direction can be prescribed to any arbitrary axis.One can receive analogous results directly from equations (3), if suppose their invariance under variations of θ (or χ).If one substitutes in equations (1) expressions for the fields E and H from (2) he receives equations for dual phase under supposition that equations for E and H have the usual form (3):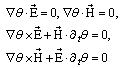 | (10) |
From the first pair of equations (10) one can receive: 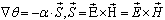 | (11a) |
S – is vector of density of energy flux of electromagnetic field, α – some co-efficient. Second pair of equations (10) leads to equation: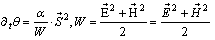 | (11b) |
W – is density of energy of electromagnetic field. Substituting (11а) in (11б) one can receive equation: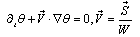 | (12) |
Here V- is a speed of electromagnetic energy propagation. If V = c, what takes place in so-called wave zone (see below), equation (12) coincides with first equation (9), where c = 1. Thus х- direction in (9) coincides with the direction of electromagnetic energy propagation. Second equation in (9) one can receive under supposition that divS = 06.
3. Solutions of the Equation for Dual Phase
a) Vacuum solution.In this case divS = 0. Solutions of the equation (9) can be received if one imposes some boundary conditions on them. Let us treat dual phase’s behaviour at the vicinity of dion. It seems naturally to suppose that far from x-axis perturbations of phase θ are small and electrodynamics’ equations have usual form corresponding to zero value of dual phase, i.e. θ = 0 asymptotically. Character feature of the equations (9) is that their solutions which are limited everywhere are absent. For instance, solution which satisfies abovementioned conditions looks as follows: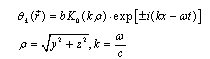 | (13) |
K0 – is modified Bessel’s function, k – wave number, ω – frequency, с – speed of light in vacuum, b – is a constant which is found from the condition of normalizing: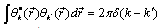 | (14) |
what leads to b = k/√π.The function K0 (z) has irregularity near z = 0. This makes interpretation of the solution (13) problematic, what is connected with arising near x – axis regions where variation of θ is of the order 2π. Let us remind that the accuracy of phase θ determination is equal to 2π, too. Implementation of quantum theory in small distances doesn’t improve situation, because quantum-mechanical phase’s operator can not be determined[9].b) Solution in electromagnetic fields of electrical dipole.Electromagnetic fields of the elementary electrical dipole which is located at point r = 0 look as follows (in spherical co-ordinates)[10]: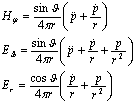 | (15) |
p(t) – is electrical moment of dipole which is directed along polar axis z; point means time derivation; с = 1. If one expresses values of S и W from (15) and substitute them in equations (11) and (12) he can find their solutions. Explicit expression for nonzero components of S looks as follows (analogous expression for W is not of very importance): | (16) |
In the wave zone 7(r >> λ, λ – wave length of radiation) one has: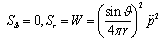 | (17) |
Then equations (11а) and (12) look as follows: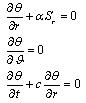 | (18) |
In last equation light speed c is written explicitly. It is obvious that its solution has a form of travelling wave θ= θ(r-ct). First two equations in (18) are equivalent to equation (11а). In order to treat their solutions one must know α. It can be done by two ways. First, if role of equation (11а) besides definition of space dependence of θ, consists in formulating initial conditions for equation (11b) too, then time derivative of its left side must equal zero8. It can be shown that it is really true if α = b/W, where b does not depend on fields E and H. Indeed, if one calculates abovementioned derivative he finds: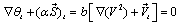 because speed V = с in wave zone. Second, one can calculate α, using equation (11а) in case of propagation of plane electromagnetic wave between two ideally reflecting mirrors and taking into account that phase redundancy Δθ is proportional to 2π along close trajectory.Solving equation (18) for α = b/W, one can find explicit expression of phase θ = -b(r – ct), what means that b = - k, where k – is wave number. It is in agreement with well-known equation[8]: ωr + kt = 0, where ω = - θt = ck, k = θr. Let us formulate boundary conditions for equation (18). Remind that it isn’t problem for calculation, but thinking: dual phase value θ = 0 near a system of electrically charged particles (elementary dipole in this case). So, whole picture of dual phase distribution for arbitrary 0 < r < ∞ and t > 0 can be found from solution of (18) with that condition: θ = 0 for r ≤ r0 , 0 < t < ∞, where r0 is sufficiently small distance. Solution of (18) looks as follows[11]: θ(r, t) = 0 for (r – r0)/c < t < ∞.One can find from equations (11) and (18) that rot grad θ ≠ 0 due to rot S ≠ 0. This means that topological structure of space near charged particles has no Euclid character.Due to theorem of duality[12] one can assert that analogous result takes place at the vicinity of elementary magnetic dipole.
because speed V = с in wave zone. Second, one can calculate α, using equation (11а) in case of propagation of plane electromagnetic wave between two ideally reflecting mirrors and taking into account that phase redundancy Δθ is proportional to 2π along close trajectory.Solving equation (18) for α = b/W, one can find explicit expression of phase θ = -b(r – ct), what means that b = - k, where k – is wave number. It is in agreement with well-known equation[8]: ωr + kt = 0, where ω = - θt = ck, k = θr. Let us formulate boundary conditions for equation (18). Remind that it isn’t problem for calculation, but thinking: dual phase value θ = 0 near a system of electrically charged particles (elementary dipole in this case). So, whole picture of dual phase distribution for arbitrary 0 < r < ∞ and t > 0 can be found from solution of (18) with that condition: θ = 0 for r ≤ r0 , 0 < t < ∞, where r0 is sufficiently small distance. Solution of (18) looks as follows[11]: θ(r, t) = 0 for (r – r0)/c < t < ∞.One can find from equations (11) and (18) that rot grad θ ≠ 0 due to rot S ≠ 0. This means that topological structure of space near charged particles has no Euclid character.Due to theorem of duality[12] one can assert that analogous result takes place at the vicinity of elementary magnetic dipole.
4. Electrodynamics of Dions.
In article[13] solutions of the Maxwell 9 equations were received for radiation field of TM-type wave with zero orbital moment momentum l = 0: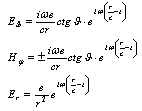 | (19) |
e – is constant. Let us prove that these fields describe radiation of dion placed at the origin of co-ordinates which phase varies linearly in time. For this consider together with (19) radiation field of TE-type wave using dual symmetry of Maxwell equation, i.e. substituting in (19) Е → -Н and Н → Е, and so as e → m: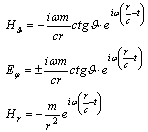 | (20) |
In article[13] an expression for electrical flow of equivalent source corresponding to (19) was found: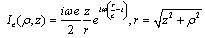 | (21) |
It is easy to find that flow of equivalent source, corresponding to (20) is: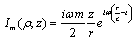 | (22) |
If one introduces value p = (e – im)e-iωt, that satisfies a condition dp/dt = 2Υ(r = 0), where Y =Ie - iIm he can rewrite (19) and (20) in a form closely looking expressions for electromagnetic fields which are radiating by electrical dipole placed at r = 0[10]: | (23) |
If factor e-iωt has been turned to the left side of (23), then this equations determine corresponding fields (23) after dual rotation on angle θ = ωt. Role of radiator plays dion which phase rotate monotonically, i.e. dion periodically turns from electric into magnetic state and vice versa. Let us remind that multipole expansion of radiation of systems consisting of charged particles of one sort only (electrical or magnetic) does not contain monopole members with l = 0. Another peculiarity of electromagnetic field of dion (19) is that it does not create gravitational field in distinction with electromagnetic fields of waves with l ≠ 0[13].
5. Discussions
This article shows that condition of “electrical” character of dual transformation’s phase can be presented as system of some equations (11) and (12). Equation (12) defines wave propagation of dual phase with speed of light in vacuum с. Due to the first order of this equation its solution has a character of divergent wave propagating from the co-ordinate’s origin to infinity. Second equation - (11а) describes structure of dual phase’s wave. This results permit to say about some mode (mass-less, Goldstone[13]), which transfers value of dual phase with speed of light from regions where that value is firmly defined either experimentally, or by agreement to other regions. It is confirmed by that this Goldstone mode is connected with breaking of dual symmetry (2) by ascribing to parameter of dual phase’s transformation θ definite, but unknown value[4]. Besides that it has a spectrum ω = ck, which is characteristic to Goldstone mode. It is connected with establishing far order in all parts of the Universe which are achievable by light signals in a sense, that fixation of the character of Maxwell’s equations in one parts transfers to another parts of the Universe. This result could shed light on questions which are connected with many-years unsuccessful searching of magnetic charges (monopoles)[15].In the article[13] this mode is supposed to be usual photons. Present results does not based on that assumption. Nonetheless all results presented here gives ground reasons to this identification. Firs of all, interaction of dions in “electrical” state must be realized by photons so as for usual electrically charged particles. Second, field which is radiated by dion is an electromagnetic one. Third, dispersion rule of that mode ω = ck has a photon-like character. And the last, if one introduces special particle which realizes all their functions parallel with photons and obeys all their features he explicitly violates the law of economy of thinking[16].Approach used in the present article differs from approach of J. Wheeler and C. Misner[2, 3], who used solutions of coupled Maxwell-Einstein equations (so called “already unified field theory” of G. Rainich[1]). Besides that only Maxwell equation are used, a case is considered which is connected with some problems in that approach. First of all, charges which create fields are concerned explicitly. Second, it is considered a case when both invariants of electromagnetic fields are equal zero. Nonetheless, results presented here in some sense are solutions of problem of dual phase’s synchronization[2] in different space parts which was initially separated by the regions where electromagnetic fields were absent. In connection with this problem it is appropriate to make a reference on[6].Present article confirms ideas expressed first by J. Wheeler that charges change Euclid structure of space-time manifold due to arising regions with non-Euclid topology at their vicinities. Thus one can concern dual phase as an example of topological (geometrical) phases[17].
Notes
1. Analogously, equations of particles` motion can be rewritten in the form, corresponding to particles with effective electric charge q.2. Analogously electric charge can be eluded in the same manner [4].3. Unpublished result, for reference see [2].4. Here we step aside from Lagrangian method evidently.5. We put c = 1 in equations (4) and below6. Equations (10) are not equivalent to the equations (6), which are corresponding to the first pair of Maxwell equations. To make equivalence complete one must add to (6) equations Ф[μν,σ]=0, what leads to the second pair [8]7. Strictly speaking, equations (11) and (12) for phase θ, are valid in the wave zone only, where conditions H2-E2=0 and EH=0 are satisfied.8. This is quite analogous to electrodynamics where one pair of Maxwell equations which does not contain time derivatives is used for formulating initial conditions for second pair equations [14].9. And of Maxwell-Einstein equation too because wave (19) does not create gravitational field [13].
References
| [1] | G.Y. Rainich. Electrodynamics of the General Relativity Theory. Trans. Am. Math. Soc. 1925, V. 27, pp. 106-130. |
| [2] | J.A. Wheeler. Neutrinos, Gravitation and Geometry. –Bologna, 1960. |
| [3] | J.A. Wheeler. Einstein Vision. Springer-Verlag. Berlin-Heidelberg-New York, 1968. |
| [4] | V.I. Strazhev, L.M. Tomil’chik. Electrodynamics with Magnetic Charge.- Minsk: “Science and Techniques”, 1975.- 336 p. |
| [5] | A.D. Dolgov. Magnetic Monopole. In book: Physical Encyclopedia in 5 volumes, V. 2, pp. 687-688.- Moscow.: “Soviet Encyclopedia”, 1990.-704 p. |
| [6] | L. Witten. Initial Value Problem of the Einstein-Maxwell Field. Phys. Rev. 1960, V. 120, No 2, pp. 635-640. |
| [7] | V.B. Berestetsky. Problems in Elementary Particles’ Physics. Moscow.: “Science”, 1979. – 256 p. |
| [8] | L.D. Landau, E.M. Lifshits Theoretical Physics. V. 2, Theory of fields. 5-th. Ed. -Moscow.: “Science”, 1967.- 460 p. |
| [9] | A.I. Bas’, Ya.B. Zel’dovich, A.M. Perelomov. Scattering, Reactions and Decays in Non-relativistic Quantum Mechanics. -Мoscow.: “Science”, 1971.-544 p. |
| [10] | J.S. Nicolis. Dynamics of Hierarchical Systems. An Evolutionary Approach.-Springer-Verlag.-1986. |
| [11] | G.B. Whitham. Linear and Nonlinear Waves. A Willey-Intersci. Pub. John Willey&Sons, 1974 |
| [12] | V.V. Nikolsky, T.I. Nikolskaya. Electrodynamics and Propagation of Radio waves.-M.: Science, 1989. – 544 p. |
| [13] | Y.N. Zayko. Explicit Solutions of Maxwell-Einstein Equations. Int. Journ. of Theor. and Math. Phys., 2011, 1(1), 12 – 16; Proc. of Saratov Univ., Ser. Physics, 2010, 1(1), 50-59. |
| [14] | J. Weber. General Relativity and Gravitational Waves.-New York, 1961.-271 p. |
| [15] | P.A.M. Dirac. Quantized singularities in the electromagnetic field. Proc. of the Royal Soc., Ser. A, 1931, V. 133, N 821. |
| [16] | R. Nevanlinna. Raum, Zeit und Relativitat.-Birkhäuserverlag, 1964. |
| [17] | M. V. Berry, Proceedings of the Royal Society of London, A, 392, 45 (1984). |

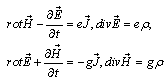
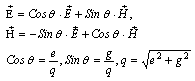
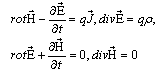
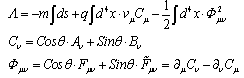
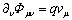
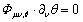
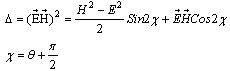
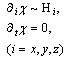
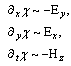
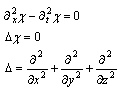
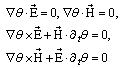
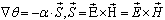
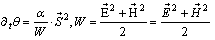
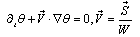
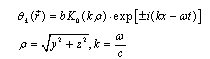
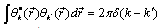
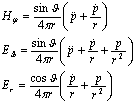

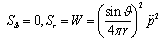
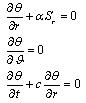
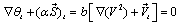 because speed V = с in wave zone. Second, one can calculate α, using equation (11а) in case of propagation of plane electromagnetic wave between two ideally reflecting mirrors and taking into account that phase redundancy Δθ is proportional to 2π along close trajectory.Solving equation (18) for α = b/W, one can find explicit expression of phase θ = -b(r – ct), what means that b = - k, where k – is wave number. It is in agreement with well-known equation[8]: ωr + kt = 0, where ω = - θt = ck, k = θr. Let us formulate boundary conditions for equation (18). Remind that it isn’t problem for calculation, but thinking: dual phase value θ = 0 near a system of electrically charged particles (elementary dipole in this case). So, whole picture of dual phase distribution for arbitrary 0 < r < ∞ and t > 0 can be found from solution of (18) with that condition: θ = 0 for r ≤ r0 , 0 < t < ∞, where r0 is sufficiently small distance. Solution of (18) looks as follows[11]: θ(r, t) = 0 for (r – r0)/c < t < ∞.One can find from equations (11) and (18) that rot grad θ ≠ 0 due to rot S ≠ 0. This means that topological structure of space near charged particles has no Euclid character.Due to theorem of duality[12] one can assert that analogous result takes place at the vicinity of elementary magnetic dipole.
because speed V = с in wave zone. Second, one can calculate α, using equation (11а) in case of propagation of plane electromagnetic wave between two ideally reflecting mirrors and taking into account that phase redundancy Δθ is proportional to 2π along close trajectory.Solving equation (18) for α = b/W, one can find explicit expression of phase θ = -b(r – ct), what means that b = - k, where k – is wave number. It is in agreement with well-known equation[8]: ωr + kt = 0, where ω = - θt = ck, k = θr. Let us formulate boundary conditions for equation (18). Remind that it isn’t problem for calculation, but thinking: dual phase value θ = 0 near a system of electrically charged particles (elementary dipole in this case). So, whole picture of dual phase distribution for arbitrary 0 < r < ∞ and t > 0 can be found from solution of (18) with that condition: θ = 0 for r ≤ r0 , 0 < t < ∞, where r0 is sufficiently small distance. Solution of (18) looks as follows[11]: θ(r, t) = 0 for (r – r0)/c < t < ∞.One can find from equations (11) and (18) that rot grad θ ≠ 0 due to rot S ≠ 0. This means that topological structure of space near charged particles has no Euclid character.Due to theorem of duality[12] one can assert that analogous result takes place at the vicinity of elementary magnetic dipole.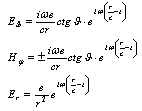
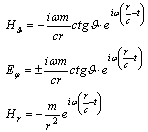
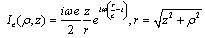
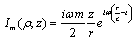

 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML