-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2012; 2(4): 67-78
doi:10.5923/j.ijtmp.20120204.03
The Meaning of Mass
1Department of Biosciences, FI-00014 University of Helsinki, Finland
2Institute of Biotechnology FI-00014 University of Helsinki, Finland
3Department of Physics, FI-00014 University of Helsinki, Finland
Correspondence to: Arto Annila, Department of Biosciences, FI-00014 University of Helsinki, Finland.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Electron, proton and neutron are described in terms of energy densities on least-action paths to show that their charges, magnetic moments and masses are manifestations of quantized geodesics. According to this geometric understanding of matter, the mass of a particle depends on how much the particle-associated curved path projects onto the straight paths of the universal surrounding energy density. The reference density of free space is embodied by the most elementary actions, the photons in propagation on their least-time paths. The vacuum density with random distribution of photon phases displays no electromagnetic field, yet the propagation of its force carriers will level off density differences. This manifests itself as gravitation. Transformations from one particle to another, for example oscillations, are described according to Noether’s theorem as changes from one action to another. This physical portrayal of quantized nature, where every entity comprises multiples of the most elementary action, parallels the atomistic tenet.
Keywords: Baryon, Geodesic, Gravitation, Lepton, Meson, Quark, Symmetry, The Principle of Least Action
Cite this paper: Arto Annila, The Meaning of Mass, International Journal of Theoretical and Mathematical Physics, Vol. 2 No. 4, 2012, pp. 67-78. doi: 10.5923/j.ijtmp.20120204.03.
Article Outline
1. Introduction
- The well-known relation E = mc2 says that the mass m of a body is the measure of bound energy E relative to the universal background, the vacuum which is characterized by permittivity
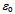 and permeablitity
and permeablitity 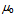 via the squared speed of light
via the squared speed of light 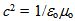 . The energy-mass relation suggests to us that a particle with non-zero mass would be a combustible entity that will ultimately transform by some mechanism to freely propagating photons. This thermodynamic tenet about matter challenges the common conceptual distinction between inertial mass, passive and active gravitational mass or between invariant and relativistic mass. Instead it simply relates a body to all other embodiments of energy via the freely propagating common background energy density.According to thermodynamics the Universe evolves from one state to another by spontaneous symmetry breaking. This notion of natural processes entails that electromagnetic radiation embodied in photons will be the final form of energy when diverse high-symmetry SU(n) systems break down in the quest to attain the ultimate equilibrium in least time[1]. The notion of heat death[2] logically implies to us that everything that exists must be ultimately composed of photons. According to this atomistic tenet the quanta that are bound in the form of a particle will eventually escape into the surroundings as free quanta, e.g., at annihilation or other transformations. In view of that the equality m = E/c2 relates energy in diverse matters to the universal energy density. Here the vacuum is not regarded as an abstract notion of a curved space-time but as a physical medium comprising the freely propagating photons that generate the lowest group of symmetry, U(1)[3]. When the distribution of photon phases is random there is no light but only density. So we reason that the mass of a body depends on how the body’s integral quanta are bound together in relation to the freely propagating photons in the universal surroundings. This geometric meaning of mass[4-6] is by no means a new notion yet it is worth to illustrate its value, for example by describing electron, proton and neutron as actions whose energy densities are on tangible paths.
. The energy-mass relation suggests to us that a particle with non-zero mass would be a combustible entity that will ultimately transform by some mechanism to freely propagating photons. This thermodynamic tenet about matter challenges the common conceptual distinction between inertial mass, passive and active gravitational mass or between invariant and relativistic mass. Instead it simply relates a body to all other embodiments of energy via the freely propagating common background energy density.According to thermodynamics the Universe evolves from one state to another by spontaneous symmetry breaking. This notion of natural processes entails that electromagnetic radiation embodied in photons will be the final form of energy when diverse high-symmetry SU(n) systems break down in the quest to attain the ultimate equilibrium in least time[1]. The notion of heat death[2] logically implies to us that everything that exists must be ultimately composed of photons. According to this atomistic tenet the quanta that are bound in the form of a particle will eventually escape into the surroundings as free quanta, e.g., at annihilation or other transformations. In view of that the equality m = E/c2 relates energy in diverse matters to the universal energy density. Here the vacuum is not regarded as an abstract notion of a curved space-time but as a physical medium comprising the freely propagating photons that generate the lowest group of symmetry, U(1)[3]. When the distribution of photon phases is random there is no light but only density. So we reason that the mass of a body depends on how the body’s integral quanta are bound together in relation to the freely propagating photons in the universal surroundings. This geometric meaning of mass[4-6] is by no means a new notion yet it is worth to illustrate its value, for example by describing electron, proton and neutron as actions whose energy densities are on tangible paths.2. Actions as Entities of Nature
- Energy is a general attribute that can be assigned to everything that exists. Yet it is a troublesome concept in the limit of infinity or singularity[7]. To this end the non-vanishing action[8,9,10] in its original form[1]
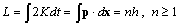 | (1) |
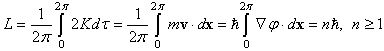 | (2) |
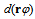 that encloses n quanta. The familiar magnitude of angular momentum
that encloses n quanta. The familiar magnitude of angular momentum 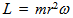 will be obtained when the precession of energy along the least-action path is given by the angular velocity
will be obtained when the precession of energy along the least-action path is given by the angular velocity 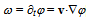 [14].The universal spectrum of photons, i.e. energy densities in free propagation, tends to be in a balance with the energy spectrum of matter, i.e. bound densities, because the free and bound forms of energy couple to each other in diverse dissipative transformations. This irrefutable conservation of quanta is apparent from the cosmic background radiation that conforms with high homogeneity to Planck’s law. Conversely, the law implies that kinetics follows from the quest for attaining the balance as soon as possible, i.e. by consuming free energy in the least time. For example, when the body moves from one state of coordination to another relative to all other bodies, free energy will be consumed. The reduction on free energy will ultimately depend on how much the universal background density in balance with all material entities will have to restructure to accommodate the body’s energy density on its curved path x. The required change dtI = L is as much as the body’s energy density on its curved path x will project non-parallel, valued by x•x = x2, onto the straight paths of surrounding energy density. Hence inertia I = ∫Ldt = mx2 is proportional to m and x2.The description of a particle as a quantized geodesic is a geometric notion. The quantity known as mass characterizes the projection of a particle’s curved path onto the reference paths of the freely propagating photons in the universal surroundings. This connection between curvature and its characteristic quantity
[14].The universal spectrum of photons, i.e. energy densities in free propagation, tends to be in a balance with the energy spectrum of matter, i.e. bound densities, because the free and bound forms of energy couple to each other in diverse dissipative transformations. This irrefutable conservation of quanta is apparent from the cosmic background radiation that conforms with high homogeneity to Planck’s law. Conversely, the law implies that kinetics follows from the quest for attaining the balance as soon as possible, i.e. by consuming free energy in the least time. For example, when the body moves from one state of coordination to another relative to all other bodies, free energy will be consumed. The reduction on free energy will ultimately depend on how much the universal background density in balance with all material entities will have to restructure to accommodate the body’s energy density on its curved path x. The required change dtI = L is as much as the body’s energy density on its curved path x will project non-parallel, valued by x•x = x2, onto the straight paths of surrounding energy density. Hence inertia I = ∫Ldt = mx2 is proportional to m and x2.The description of a particle as a quantized geodesic is a geometric notion. The quantity known as mass characterizes the projection of a particle’s curved path onto the reference paths of the freely propagating photons in the universal surroundings. This connection between curvature and its characteristic quantity 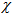 proportional to m is familiar, e.g., from the theorem of Gauss and Bonnet. It sums up the geodesic curvature kg = n∞ ∙ (x´ × x´´)/|x´|3 along its path x, as a projection on the universal surroundings with normal n∞, to the Euler characteristic
proportional to m is familiar, e.g., from the theorem of Gauss and Bonnet. It sums up the geodesic curvature kg = n∞ ∙ (x´ × x´´)/|x´|3 along its path x, as a projection on the universal surroundings with normal n∞, to the Euler characteristic 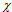 = ||kgdx|| (Fig. 1). Also the numbers of Chern are topologically invariant characteristics of vector bundles on a smooth manifold[15]. Moreover, the geometric notion of action as a quantized path is also expressed mathematically by Taniyama-Shimura conjecture which says that every elliptic curve is a modular[16].Of course, the least-action path is a familiar notion from celestial mechanics and optics[9,17,18,19,20]. From these preliminaries to the holistic and atomistic worldview, where all entities of nature are pictured as interacting actions composed of photon multiples[1,10], we will proceed to describe some elementary particles as actions.
= ||kgdx|| (Fig. 1). Also the numbers of Chern are topologically invariant characteristics of vector bundles on a smooth manifold[15]. Moreover, the geometric notion of action as a quantized path is also expressed mathematically by Taniyama-Shimura conjecture which says that every elliptic curve is a modular[16].Of course, the least-action path is a familiar notion from celestial mechanics and optics[9,17,18,19,20]. From these preliminaries to the holistic and atomistic worldview, where all entities of nature are pictured as interacting actions composed of photon multiples[1,10], we will proceed to describe some elementary particles as actions. 3. The Photon as the Most Elementary Action
- A single quantum in the form of a photon is the absolutely least action. Its momentum p on the oriented and indivisible path of wavelength x quantifies Planck’s constant h. Conversely, the
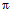 -shifted photon, i.e. the complex conjugate of
-shifted photon, i.e. the complex conjugate of , is the oppositely polarized action known as the antiphoton
, is the oppositely polarized action known as the antiphoton 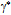 (Fig. 2). While photons embody electric field, i.e. the electromagnetic potential energy gradient, the electromagnetic force will vanish for a pair of co-propagating
(Fig. 2). While photons embody electric field, i.e. the electromagnetic potential energy gradient, the electromagnetic force will vanish for a pair of co-propagating  and
and  *. The cancellation of photon phases, however, does not cancel the energy density of the
*. The cancellation of photon phases, however, does not cancel the energy density of the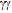 * pair. That carrier of energy will contribute to the vacuum’s potential along with all other co-propagating pairs. In other words, when photons propagate in all directions, but on the average in the pairs of opposite phases, there is no light but the space still embodies energy density. Therefore the universal vacuum does not exert electromagnetic force. Nevertheless, it possesses the electromagnetic characteristics
* pair. That carrier of energy will contribute to the vacuum’s potential along with all other co-propagating pairs. In other words, when photons propagate in all directions, but on the average in the pairs of opposite phases, there is no light but the space still embodies energy density. Therefore the universal vacuum does not exert electromagnetic force. Nevertheless, it possesses the electromagnetic characteristics 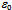 and
and 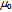 . The co-propagating quanta level off energy density differences at the speed of light[21]. The all-round non-zero universal energy density contained in the generators of the lowest group of symmetry tends to be in balance with all other densities whose generators belong to diverse groups of higher symmetry. The physical character of vacuum manifests itself in a variety of ways, most notably in Casimir effects[22-24], double-slit experiments[25] including the Aharanov-Bohm effect[26] as well as in propagation of light, perihelion precession, geodetic and frame dragging effects, galactic lensing and rotation[18,19,20,27], and eventually also in anomalous acceleration[28,29].The co-propagating
. The co-propagating quanta level off energy density differences at the speed of light[21]. The all-round non-zero universal energy density contained in the generators of the lowest group of symmetry tends to be in balance with all other densities whose generators belong to diverse groups of higher symmetry. The physical character of vacuum manifests itself in a variety of ways, most notably in Casimir effects[22-24], double-slit experiments[25] including the Aharanov-Bohm effect[26] as well as in propagation of light, perihelion precession, geodetic and frame dragging effects, galactic lensing and rotation[18,19,20,27], and eventually also in anomalous acceleration[28,29].The co-propagating 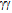 * pair is an open action, i.e., a boson that sums up to a spin-2 force carrier. It will emerge in free propagation when two neutral bodies move relative to each other, just as a single photon will escape in free propagation when two charged actions move relative to each other. In accordance with Lorenz gauge ∂t
* pair is an open action, i.e., a boson that sums up to a spin-2 force carrier. It will emerge in free propagation when two neutral bodies move relative to each other, just as a single photon will escape in free propagation when two charged actions move relative to each other. In accordance with Lorenz gauge ∂t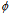 + c2∇•A = 0, a change in the scalar potential
+ c2∇•A = 0, a change in the scalar potential 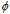 will invariably relate to the net flux of energy down along the gradient of vector potential[30]. In a thermodynamic balance the opposing to-and-fro fluxes are equal in magnitude. Since the vector character vanishes, only the length (A*A)½ of the steady-state interaction potential contributes as a scalar to the vacuum density. In general, force carriers of any kind are quantized flows of energy that propagate to diminish forces[10,31]. The consumption of free energy by a net flow of energy embodies an irreversible flow of time[32].The photons will break free from diverse curved circulations of bound quanta, when these fermions open up to change from one state of action to another. For example, when an atomic system contracts from an exited state to the ground state, a train of photons will break free from the standing energy density wave between an electron and a nucleus to a sparser surrounding density. Likewise, when two net neutral bodies move toward each other, pairs of oppositely polarized photons, coined here as gravitons, will break free from the standing energy density waves between the bodies to the surrounding sparser vacuum. Conversely, the two bodies will depart from each other when their surroundings are rich in actions to supply the sparser space between the bodies with more energy dense actions[10,20].A change of state, irrespective whether it manifest itself as attraction or repulsion, will happen to level off forces, i.e. curvatures[33], between the system and its surroundings[10]. For example, a chemical reaction will progress toward a stationary-state balance in the respective surroundings either by absorbing or emitting quanta. The quest for the balance between bound and free forms of energy will manifests itself so also that photons will shift frequencies to adapt their energy density to the surrounding energy densities, e.g., when propagating through a varying gravitational potential[18,34]. In all cases, the superior surroundings will force the system in evolution to attain a stationary state in the least time.At the stationary state the photons propagate back and forth so that there is no net flow of energy between the system and its surroundings (Fig. 2). The modulus of a standing density wave can be regarded as a boson (referred to as Higgs particle in some theories). It has no net spin because the spins of the two pairs of co-propagating
will invariably relate to the net flux of energy down along the gradient of vector potential[30]. In a thermodynamic balance the opposing to-and-fro fluxes are equal in magnitude. Since the vector character vanishes, only the length (A*A)½ of the steady-state interaction potential contributes as a scalar to the vacuum density. In general, force carriers of any kind are quantized flows of energy that propagate to diminish forces[10,31]. The consumption of free energy by a net flow of energy embodies an irreversible flow of time[32].The photons will break free from diverse curved circulations of bound quanta, when these fermions open up to change from one state of action to another. For example, when an atomic system contracts from an exited state to the ground state, a train of photons will break free from the standing energy density wave between an electron and a nucleus to a sparser surrounding density. Likewise, when two net neutral bodies move toward each other, pairs of oppositely polarized photons, coined here as gravitons, will break free from the standing energy density waves between the bodies to the surrounding sparser vacuum. Conversely, the two bodies will depart from each other when their surroundings are rich in actions to supply the sparser space between the bodies with more energy dense actions[10,20].A change of state, irrespective whether it manifest itself as attraction or repulsion, will happen to level off forces, i.e. curvatures[33], between the system and its surroundings[10]. For example, a chemical reaction will progress toward a stationary-state balance in the respective surroundings either by absorbing or emitting quanta. The quest for the balance between bound and free forms of energy will manifests itself so also that photons will shift frequencies to adapt their energy density to the surrounding energy densities, e.g., when propagating through a varying gravitational potential[18,34]. In all cases, the superior surroundings will force the system in evolution to attain a stationary state in the least time.At the stationary state the photons propagate back and forth so that there is no net flow of energy between the system and its surroundings (Fig. 2). The modulus of a standing density wave can be regarded as a boson (referred to as Higgs particle in some theories). It has no net spin because the spins of the two pairs of co-propagating 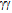 * add up to zero as they are opposite to each other. These co-carriers constitute the stationary vacuum, whose energy density is contained in the two complex conjugated vector potentials. Therefore its vector character disappears and the photon-embodied vacuum appears as a scalar potential. These bosons as the generators of the lowest group of symmetry embody the universal geodesics. They provide the reference for all other actions that are generators of higher groups of symmetry. In other words, the mass of a particle characterizes the curvature of the corresponding bound action in relation to the physical vacuum composed of freely propagating actions. Since the mass of a particle reports from the geodesic relation to the background density, cross sections of diverse particles are observed on top of the background density.
* add up to zero as they are opposite to each other. These co-carriers constitute the stationary vacuum, whose energy density is contained in the two complex conjugated vector potentials. Therefore its vector character disappears and the photon-embodied vacuum appears as a scalar potential. These bosons as the generators of the lowest group of symmetry embody the universal geodesics. They provide the reference for all other actions that are generators of higher groups of symmetry. In other words, the mass of a particle characterizes the curvature of the corresponding bound action in relation to the physical vacuum composed of freely propagating actions. Since the mass of a particle reports from the geodesic relation to the background density, cross sections of diverse particles are observed on top of the background density.4. The Neutrino as the Basic Bound Action
- We consider the neutrino
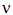 as the most elementary bound action. The associated angular momentum
as the most elementary bound action. The associated angular momentum 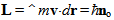 points along the unit vector no that defines the plane of propagation for a left-handed closed circulation (Fig. 3). The planar geodesic, i.e. the ground flavor
points along the unit vector no that defines the plane of propagation for a left-handed closed circulation (Fig. 3). The planar geodesic, i.e. the ground flavor 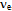 , has no curvature in relation to a perfectly flat, i.e. Euclidean surroundings. Thus the mass of
, has no curvature in relation to a perfectly flat, i.e. Euclidean surroundings. Thus the mass of 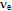 is tiny in relation to the minute universal curvature. We assign the one-quantum ring as the generator of the cyclic group canonically isomorphic to U(1). Conversely, the antineutrino
is tiny in relation to the minute universal curvature. We assign the one-quantum ring as the generator of the cyclic group canonically isomorphic to U(1). Conversely, the antineutrino 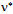 constitutes one integral circulation of opposite handedness which is usually referred to as the spin. Hence neutrinos and antineutrinos of the same flavor distinguish from each other only when in relation to a reference (an observer).
constitutes one integral circulation of opposite handedness which is usually referred to as the spin. Hence neutrinos and antineutrinos of the same flavor distinguish from each other only when in relation to a reference (an observer). and conversely
and conversely 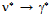 . The equivalence between the most elementary bound and free action is contained in the canonical commutation relation[p,x] = –iħ. Accordingly, the annihilation of v with
. The equivalence between the most elementary bound and free action is contained in the canonical commutation relation[p,x] = –iħ. Accordingly, the annihilation of v with 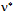 will dissipate
will dissipate  and
and 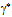 . In contrast to the neutrino theory of light[35], the neutrino-antineutrino pair does not relate to a single photon but to the pair of
. In contrast to the neutrino theory of light[35], the neutrino-antineutrino pair does not relate to a single photon but to the pair of  and
and 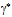 .
.5. The Electron as a Toroidal Action
- The energy density of contemporary cosmos is low. This entails to us that the most common forms of bound energy are actions whose geodesics will project only little onto the universal surroundings. This conclusion prompts us to regard elementary particles as closed circulations whose quanta pair with one another mostly at opposite phases. When the phases and paths of quanta are mostly opposite, i.e. dtI 0, the projection onto the present-day universal surroundings will be small.The Universe of today is on the average almost flat. Its radius R = cT has grown huge due to irrevocable unfolding of actions during the past T = 13.7 billion years in the quest of a stationary state in the “zero-density surroundings”. In geometric terms the present-day sparse surroundings are least perturbed by least-action paths whose projections are low on the average and whose winding numbers total to zero to comply with neutrality.The electron e– is a stationary-state action, i.e., dtL = 0. The elementary charge
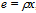 , as a conserved quantity, stems from the windings of a circulating density
, as a conserved quantity, stems from the windings of a circulating density 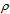 on a chiral path of length x. The surrounding inter-actions that constitute the vacuum, will adapt to this Noetherian current density
on a chiral path of length x. The surrounding inter-actions that constitute the vacuum, will adapt to this Noetherian current density 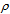 dx/dt on its chiral path by generating a field E. According to Gauss’ law the density of the field sumps up to a constant 2K = ∫
dx/dt on its chiral path by generating a field E. According to Gauss’ law the density of the field sumps up to a constant 2K = ∫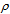 v•Edt = ∫
v•Edt = ∫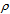 E•dx =
E•dx = 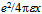 . Thus the stationary action can be quantified relative to the most basic bound action ħ by a dimensionless coupling constant
. Thus the stationary action can be quantified relative to the most basic bound action ħ by a dimensionless coupling constant 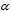 = L/ħ = ∫2Kdt/ħ =
= L/ħ = ∫2Kdt/ħ = 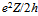 when denoting the vacuum impedance
when denoting the vacuum impedance 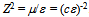 . In this way
. In this way 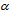 relates the electromagnetic inter-action with the most elementary action, the strong interaction characterized by ħ which is often assigned to unity.The unit charge e–, magnetic moment
relates the electromagnetic inter-action with the most elementary action, the strong interaction characterized by ħ which is often assigned to unity.The unit charge e–, magnetic moment 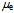 as well as the low mass me of electron encourages us to re-inspect a torus as the geodesic of the electron’s action[36,37] because a toroidal circulation will generate an electric charge and a magnetic moment. Considering that when any two loops are exactly at opposite phases, their projections will cancel each other perfectly, the dense toroidal windings will project only little onto the sparse surrounding energy density. The degree of self-cancellation is high in the torus, but not complete as each quantum on the rising helical path is not perfectly planar, but accrues a slight torsion and falls short a bit from making the
as well as the low mass me of electron encourages us to re-inspect a torus as the geodesic of the electron’s action[36,37] because a toroidal circulation will generate an electric charge and a magnetic moment. Considering that when any two loops are exactly at opposite phases, their projections will cancel each other perfectly, the dense toroidal windings will project only little onto the sparse surrounding energy density. The degree of self-cancellation is high in the torus, but not complete as each quantum on the rising helical path is not perfectly planar, but accrues a slight torsion and falls short a bit from making the  -ring closure. Therefore the number of quanta must exceed at least by one the number of windings for the modular path to close exactly. The fine structure constant
-ring closure. Therefore the number of quanta must exceed at least by one the number of windings for the modular path to close exactly. The fine structure constant 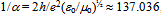 , available from measurements of quantized conductance
, available from measurements of quantized conductance 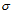 = e2/h, implies to us that the electron is a
= e2/h, implies to us that the electron is a 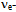 handed torus with 137 windings so that the geodesic closes exactly with 138 quanta (Fig. 4). Hence we designate e– as the generator of the chiral symmetry group SU(138).The length of least-action path
handed torus with 137 windings so that the geodesic closes exactly with 138 quanta (Fig. 4). Hence we designate e– as the generator of the chiral symmetry group SU(138).The length of least-action path 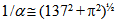 suggests to us to consider the electron as if it consisted of a circular array of 137 perfectly planar rings with normal vectors no and of one circulation in the orthogonal direction that rolls over once along the peripheral perimeter of the torus. This practical approximation of the curved, quantized geodesic by orthogonal linear decomposition, in essence a Hopf fibration[38], means as if me = 0.511 MeV/c2[39] were to stem only from the single peripheral quantum because the array of planar rings where any two having exactly opposite phases, does not perturb the energy density of the flat surroundings at all. Geometrically speaking, the sum of projections over the circular array of evenly spaced rings will vanish in relation to any reference direction
suggests to us to consider the electron as if it consisted of a circular array of 137 perfectly planar rings with normal vectors no and of one circulation in the orthogonal direction that rolls over once along the peripheral perimeter of the torus. This practical approximation of the curved, quantized geodesic by orthogonal linear decomposition, in essence a Hopf fibration[38], means as if me = 0.511 MeV/c2[39] were to stem only from the single peripheral quantum because the array of planar rings where any two having exactly opposite phases, does not perturb the energy density of the flat surroundings at all. Geometrically speaking, the sum of projections over the circular array of evenly spaced rings will vanish in relation to any reference direction 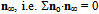
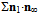 > 0. In other words the total projection of the electron’s action onto the surrounding actions will manifest itself as me > 0. Alternatively, we may think that a single, non-Euclidean loop quantum, as it were removed from the torus of 138 quanta, would project
> 0. In other words the total projection of the electron’s action onto the surrounding actions will manifest itself as me > 0. Alternatively, we may think that a single, non-Euclidean loop quantum, as it were removed from the torus of 138 quanta, would project 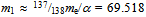 MeV/c2 onto the vacuum. In the following we will use this value to quantify an element of the toroidal geodesic when calculating elementary estimates of masses from diverse geodesics that comprise toroidal arrays of the 1st generation quanta.Also the electron’s magnetic moment can be estimated from the toroidal geodesic. When the rolling peripheral path of the total circulation is decomposed further to the primary planar portion
MeV/c2 onto the vacuum. In the following we will use this value to quantify an element of the toroidal geodesic when calculating elementary estimates of masses from diverse geodesics that comprise toroidal arrays of the 1st generation quanta.Also the electron’s magnetic moment can be estimated from the toroidal geodesic. When the rolling peripheral path of the total circulation is decomposed further to the primary planar portion 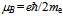 along
along 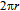 with velocity v =
with velocity v = 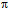 c/137 and to the secondary circulation on the orthogonal path
c/137 and to the secondary circulation on the orthogonal path 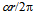 with velocity c (Fig. 4), the magnetic moment is found to be
with velocity c (Fig. 4), the magnetic moment is found to be 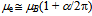 [40]. Thus the elementary decomposition of electron’s curved geodesic to the orthogonal Euclidean paths provides us with insight to the anomaly in
[40]. Thus the elementary decomposition of electron’s curved geodesic to the orthogonal Euclidean paths provides us with insight to the anomaly in 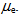 A precise calculation would track the actual geodesic[41] according to
A precise calculation would track the actual geodesic[41] according to 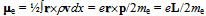 using the radius r and its cross product with velocity v.Conversely, the positron e+ can be regarded as the
using the radius r and its cross product with velocity v.Conversely, the positron e+ can be regarded as the 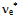 -handed quantized torus. It will project the same me onto the surroundings but the opposite sense of circulation will induce electromagnetic field of opposite sign that manifests itself as the opposite charge and magnetic moment. The decomposition of toroidal geodesic to the orthogonal planar circulations explains the annihilation of e+ with e– so that the anti-parallel rays of
-handed quantized torus. It will project the same me onto the surroundings but the opposite sense of circulation will induce electromagnetic field of opposite sign that manifests itself as the opposite charge and magnetic moment. The decomposition of toroidal geodesic to the orthogonal planar circulations explains the annihilation of e+ with e– so that the anti-parallel rays of 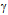 and
and 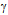 * will burst out from the two opposing peripheral circulations. Under high-energy circumstances, e.g., generated by particle accelerators, the e+e– annihilation may also yield a pair of bosons, known as W– and its antiparticle W+, or produce the net neutral boson known as Z.The description of electron as the toroidal action exemplifies that the charge, magnetic moment and mass have the common topological origin. The surrounding photons will accommodate the electron by adjusting their density to match me and by adjusting their irrotational and solenoidal phase density to match e– and
* will burst out from the two opposing peripheral circulations. Under high-energy circumstances, e.g., generated by particle accelerators, the e+e– annihilation may also yield a pair of bosons, known as W– and its antiparticle W+, or produce the net neutral boson known as Z.The description of electron as the toroidal action exemplifies that the charge, magnetic moment and mass have the common topological origin. The surrounding photons will accommodate the electron by adjusting their density to match me and by adjusting their irrotational and solenoidal phase density to match e– and 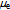 . Since the curvature and chirality characterize the same action, the surrounding gravitational and electromagnetic fields are in an innate relation to each other. Moreover, since both fields are responses of the surrounding inter-actions to the same geodesic, also their functional form is the same. The ratio of the radius of the Universe and the radius of electron yields the ratio of electrostatic to the gravitational coupling constants
. Since the curvature and chirality characterize the same action, the surrounding gravitational and electromagnetic fields are in an innate relation to each other. Moreover, since both fields are responses of the surrounding inter-actions to the same geodesic, also their functional form is the same. The ratio of the radius of the Universe and the radius of electron yields the ratio of electrostatic to the gravitational coupling constants 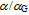 =
= 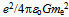 . The factor
. The factor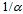 in Eq. 3 precedes the familiar factor
in Eq. 3 precedes the familiar factor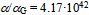 since we chose to express
since we chose to express 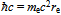 =
=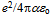 using the fine-structure constant. For a stable particle the least action implies a balance of forces me/re2 = M/R2, i.e. the Gaussian curvature of the electron of re weighted by me equals that of the Universe of total mass M =
using the fine-structure constant. For a stable particle the least action implies a balance of forces me/re2 = M/R2, i.e. the Gaussian curvature of the electron of re weighted by me equals that of the Universe of total mass M =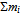 and radius R[19,42]. Also the equality
and radius R[19,42]. Also the equality 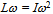 = 2K = mv2 = Ev2/c2 informs us that the kinetic energy on the geodesic is in relation to the universal energy density via the index of refraction n = c/v. Thus, the photon wavelength
= 2K = mv2 = Ev2/c2 informs us that the kinetic energy on the geodesic is in relation to the universal energy density via the index of refraction n = c/v. Thus, the photon wavelength 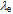 =
= 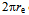 of annihilation, as such, does not equate with the radius of electron but first via the refractive index.
of annihilation, as such, does not equate with the radius of electron but first via the refractive index.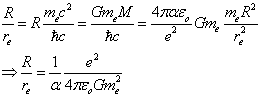 | (3) |
6. Nucleons as Tetrahedral Actions
- Noether’s theorem about stationary actions[8] encourages us to consider also nucleons as circulations of energy densities on modular least-action paths. Since the charges of quarks are integer fractions of e, we will construct the proton as a closed circulation where two up quarks, each comprising a 2/3-fraction of e+, and one down quark, as a 1/3-fraction of e–, are glued together by high-frequency photons. Similarly, we will construct the neutron from one u-quark and two d-quarks. Since the full
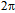 -torus contains 138 quanta, the u-quark, that spans the
-torus contains 138 quanta, the u-quark, that spans the 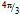 -arc, will contain 92 quanta and the d-quark, that spans the
-arc, will contain 92 quanta and the d-quark, that spans the 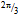 -arc, will comprise 46 quanta. Hence we assign u and d as the generators of chiral symmetry groups SU(92) and SU(46). The u-quark accrues
-arc, will comprise 46 quanta. Hence we assign u and d as the generators of chiral symmetry groups SU(92) and SU(46). The u-quark accrues 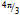 -phase along its path due to the helical pitch and similarly d accumulates
-phase along its path due to the helical pitch and similarly d accumulates 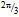 -phase along its curved helical path. Therefore the three quarks will coordinate relative to each other so that one quark is on each face of a tetrahedron. One quark will bridge over to another quark by a short wavelength photon, known as the gluon g (Fig. 5). Since the action is a directional path, the two quarks of the same flavor are distinguishable from each other in a nucleon. This is in accordance with the notion of color in quantum chromodynamics.
-phase along its curved helical path. Therefore the three quarks will coordinate relative to each other so that one quark is on each face of a tetrahedron. One quark will bridge over to another quark by a short wavelength photon, known as the gluon g (Fig. 5). Since the action is a directional path, the two quarks of the same flavor are distinguishable from each other in a nucleon. This is in accordance with the notion of color in quantum chromodynamics.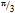 -arcs of u will amount only to ⅓me. In contrast, the three
-arcs of u will amount only to ⅓me. In contrast, the three 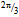 -arcs of quarks each at a distinct face of the tetrahedron will give rise to most of mN. Specifically, the pairs of loop quanta will contribute more and more mass as the two arcs of quarks diverge from their minimum mutual projection at the joining gluon toward the maximum at the
-arcs of quarks each at a distinct face of the tetrahedron will give rise to most of mN. Specifically, the pairs of loop quanta will contribute more and more mass as the two arcs of quarks diverge from their minimum mutual projection at the joining gluon toward the maximum at the 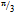 mid-point of an arc. The 3∙23 = 69 rings along the three
mid-point of an arc. The 3∙23 = 69 rings along the three 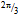 -arcs project on the surroundings an elementary estimate of mN =
-arcs project on the surroundings an elementary estimate of mN = 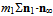 ≈ 937.54 MeV/c2. In this way we will obtain nearly equal estimates (mN + 5/3me) and (mN + 4/3me) for the proton p+ and neutron n, although their paths differ by length and by the net number of chiral windings that lead substantial differences in the charge and magnetic moment. The differences between our elementary estimates obtained from the projections and the measured values mp+ = 938.27 MeV/c2 and mn = 939.57 MeV/c2[39] will narrow when the tetrahedral coordination of p+ and n are allowed for slight distortions.The proposed least-action paths of proton and neutron provide us also with elementary estimates of their magnetic moments. When the curved path of
≈ 937.54 MeV/c2. In this way we will obtain nearly equal estimates (mN + 5/3me) and (mN + 4/3me) for the proton p+ and neutron n, although their paths differ by length and by the net number of chiral windings that lead substantial differences in the charge and magnetic moment. The differences between our elementary estimates obtained from the projections and the measured values mp+ = 938.27 MeV/c2 and mn = 939.57 MeV/c2[39] will narrow when the tetrahedral coordination of p+ and n are allowed for slight distortions.The proposed least-action paths of proton and neutron provide us also with elementary estimates of their magnetic moments. When the curved path of 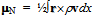 is decomposed in orthogonal rings as done before for the electron, estimates are
is decomposed in orthogonal rings as done before for the electron, estimates are 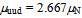 and
and 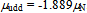 . Moreover, when the quarks at the tetrahedron’s faces are tilted by few degrees about the interconnecting gluons, our elementary estimates will home in on the experimental values
. Moreover, when the quarks at the tetrahedron’s faces are tilted by few degrees about the interconnecting gluons, our elementary estimates will home in on the experimental values 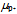 =
= 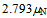 and
and 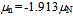 [39]. All in all, the description of nucleons as actions also exemplifies the common geometric origin of charge, magnetic moment and mass.Conversely, the anti-proton and anti-neutron can be constructed from the anti-quarks u* and d* that differ from u and d only by having the opposite sense of helical winding. Therefore, we regard matter over antimatter nothing but the dominant chirality consensus of bound quanta. The standard way of distributing the opposite chiral circulations among constituents of matter complies with overall neutrality. In other words, the neutrality means that the dispersion of phases of free quanta is random. Thus the handedness is not a consequence of some putative fierce annihilation at the “beginning”, but presumably the chirality consensus settled at baryogenesis. We see the present-day particles as outcomes of prior processes where the chirality standard was established to facilitate the least-time consumption of free energy. The same least-time principle rationalizes also the emergence of molecular chirality standards during the evolution of biota[43]. In general, the thermodynamic tenet regards any embodiment of quanta as a means that facilitates the least-time leveling off energy differences.
[39]. All in all, the description of nucleons as actions also exemplifies the common geometric origin of charge, magnetic moment and mass.Conversely, the anti-proton and anti-neutron can be constructed from the anti-quarks u* and d* that differ from u and d only by having the opposite sense of helical winding. Therefore, we regard matter over antimatter nothing but the dominant chirality consensus of bound quanta. The standard way of distributing the opposite chiral circulations among constituents of matter complies with overall neutrality. In other words, the neutrality means that the dispersion of phases of free quanta is random. Thus the handedness is not a consequence of some putative fierce annihilation at the “beginning”, but presumably the chirality consensus settled at baryogenesis. We see the present-day particles as outcomes of prior processes where the chirality standard was established to facilitate the least-time consumption of free energy. The same least-time principle rationalizes also the emergence of molecular chirality standards during the evolution of biota[43]. In general, the thermodynamic tenet regards any embodiment of quanta as a means that facilitates the least-time leveling off energy differences.7. Electron Capture as a Natural Process
- Evolution by symmetry breaking will become more tangible when paths of energy dispersal can be illustrated. Here we will outline electron capture as a change from the actions of proton and electron to the action of neutron.The natural process will commence in the energy-dense surroundings of a nucleus when an electron confines next to an up quark of proton. The torus of e will excise open to become the
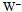 boson when one quantum loop annihilates with an antineutrino,
boson when one quantum loop annihilates with an antineutrino, 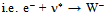 (Fig. 6). Notably, despite the one loop quantum annihilation the charge of W equals the elementary charge
(Fig. 6). Notably, despite the one loop quantum annihilation the charge of W equals the elementary charge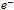 because the opposing peripheral circulation of
because the opposing peripheral circulation of 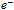 is also cut open. Hence the sum of circulations that generates the total charge remains the same. Conversely,
is also cut open. Hence the sum of circulations that generates the total charge remains the same. Conversely, 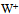 is the open action of the opposite handedness resulting from
is the open action of the opposite handedness resulting from 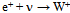 .The transformation from
.The transformation from 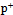 to n will proceed so that an open, hence reactive end of
to n will proceed so that an open, hence reactive end of 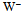 will attack the front-end of the adjacent u quark at the gluon. The commencing annihilation will consume
will attack the front-end of the adjacent u quark at the gluon. The commencing annihilation will consume 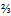 of
of 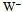 in the unfolding of u. The residual
in the unfolding of u. The residual 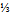 of
of 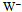 will subsequently adopt the least-action path of d quark by subsuming
will subsequently adopt the least-action path of d quark by subsuming  when the circulation closes. When the resulting udd baryon has settled down from eventual excitations, it is the neutron.
when the circulation closes. When the resulting udd baryon has settled down from eventual excitations, it is the neutron.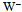 contains some short wavelength characteristic that will perturb the surrounding density substantially. We suggest that mW± stems primarily from the gap that resulted when one loop was excised from the electron torus at the
contains some short wavelength characteristic that will perturb the surrounding density substantially. We suggest that mW± stems primarily from the gap that resulted when one loop was excised from the electron torus at the 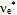 annihilation. The dimension of the one-loop gap, on the order of
annihilation. The dimension of the one-loop gap, on the order of 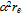 , is matched by high-frequency photons in the surrounding energy density spectrum. This balance manifests itself as the huge mass. Thus
, is matched by high-frequency photons in the surrounding energy density spectrum. This balance manifests itself as the huge mass. Thus 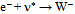 is a striking example of a change in action that causes dramatic changes in curvature that relate to substantial changes in mass.Likewise, the Z boson can be pictured as a compound particle
is a striking example of a change in action that causes dramatic changes in curvature that relate to substantial changes in mass.Likewise, the Z boson can be pictured as a compound particle 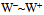 where the two excided tori of opposite handedness are linked across the gap by a high-frequency photon, i.e. gluon (~). We reason the gap in Z will account for the most of mZ = 91.2 GeV/c2[39]. Conversely, the antiparticle Z* is the reversed path of
where the two excided tori of opposite handedness are linked across the gap by a high-frequency photon, i.e. gluon (~). We reason the gap in Z will account for the most of mZ = 91.2 GeV/c2[39]. Conversely, the antiparticle Z* is the reversed path of 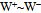 , but Z* is Z itself in accordance with CPT symmetry.It is noteworthy that the reaction
, but Z* is Z itself in accordance with CPT symmetry.It is noteworthy that the reaction 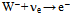 may fail to complete the electron torus but arrives at pion
may fail to complete the electron torus but arrives at pion 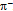 . Our mass estimate of this 1st generation pseudoscalar meson with u~d* composition
. Our mass estimate of this 1st generation pseudoscalar meson with u~d* composition 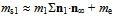 = 139.55 MeV/c2 comes close to
= 139.55 MeV/c2 comes close to 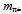 = 139.57 MeV/c2[39] by acknowledging that in
= 139.57 MeV/c2[39] by acknowledging that in 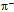 when described in terms of 2∙46 = 92 quantum loops along the
when described in terms of 2∙46 = 92 quantum loops along the 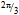 -arcs of d and
-arcs of d and 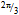 -arc fraction of u*, although in the same plane, will fail to pair perfectly anti-parallel because of the phase offset that accrues along the path (Fig. 7). When
-arc fraction of u*, although in the same plane, will fail to pair perfectly anti-parallel because of the phase offset that accrues along the path (Fig. 7). When 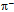 decays to leptons, the torus will reclose so that the gluon (~) will transform to an antineutrino, i.e., u*~ d → u*d +
decays to leptons, the torus will reclose so that the gluon (~) will transform to an antineutrino, i.e., u*~ d → u*d + 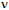 * =
* = 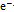 +
+ 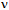 *. The mass of the vector meson rho
*. The mass of the vector meson rho 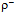 differs from
differs from 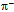 although both are composed of u* and d. We understand that the two quarks of
although both are composed of u* and d. We understand that the two quarks of 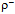 are glued together on the adjacent faces of tetrahedron whereas in
are glued together on the adjacent faces of tetrahedron whereas in 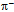 they are on the same plane (Fig. 7). The decomposition of the u~d* path of
they are on the same plane (Fig. 7). The decomposition of the u~d* path of 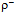 , as before, provides us with an elementary estimate of the total projection
, as before, provides us with an elementary estimate of the total projection 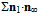 relative to the universal surroundings. It corresponds to the mass of 1st-generation vector meson mv1 =
relative to the universal surroundings. It corresponds to the mass of 1st-generation vector meson mv1 = 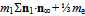 ≈ 775.82 MeV/c2 in a good agreement with
≈ 775.82 MeV/c2 in a good agreement with 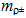 = 775.49 MeV/c2[39]. Since the topologies of
= 775.49 MeV/c2[39]. Since the topologies of 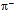 and
and 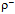 differ, also their channels of decay are different.
differ, also their channels of decay are different.8. Elementary Diversity
- The energy density of contemporary universal surroundings is on the average too sparse to support much of the known plethora of particles above the ground-state actions. Consequently diverse flavors and various resonances are found first under high-energy circumstances such as those fabricated by particle accelerators and those presumably prevailing in stars or other powerful celestial mechanisms that can break strongly bound actions. Since the 2nd and 3rd generation particles share the 1st generation’s basic character, we reason that higher masses of the excited strings reflect some additional curvature about the ground-state ring, toroidal and tetrahedral topologies (Figs. 8 and 9). Likewise, we regard resonant states as topological fluctuations and oscillations as repetitive transitions from one action to another.We expect that the 1st generation planar ring
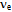 will acquire more curvature when immersed in high-density surroundings, by transforming to the 2nd-generation
will acquire more curvature when immersed in high-density surroundings, by transforming to the 2nd-generation 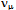 or eventually to the 3rd generation
or eventually to the 3rd generation 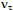 . Since the neutrino masses are not known, we have no firm ground to propose how these particular paths would look like. Nevertheless, clues about bent or twisted paths could come from known conformations of strained rings as well as from results of ring theory. In any case we expect according to the general principle of symmetry breaking that when one topology transforms to another, the neutrino circulation will open up in one generation, twist and close down in another. A non-equilibrium nascent flavor may process coherently via oscillatory propagation toward a mature stationary-state admixture of flavors governed by the surrounding energy density of the dominating chirality consensus.Likewise, we expect that when
. Since the neutrino masses are not known, we have no firm ground to propose how these particular paths would look like. Nevertheless, clues about bent or twisted paths could come from known conformations of strained rings as well as from results of ring theory. In any case we expect according to the general principle of symmetry breaking that when one topology transforms to another, the neutrino circulation will open up in one generation, twist and close down in another. A non-equilibrium nascent flavor may process coherently via oscillatory propagation toward a mature stationary-state admixture of flavors governed by the surrounding energy density of the dominating chirality consensus.Likewise, we expect that when 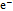 breaks open, the array of loop quanta will acquire more curvature in high-density surroundings so that
breaks open, the array of loop quanta will acquire more curvature in high-density surroundings so that 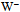 will close as the muon
will close as the muon 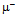 to display
to display 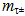 = 105.66 MeV/c2[39] or eventually wind up with further curvature and close as the tauon
= 105.66 MeV/c2[39] or eventually wind up with further curvature and close as the tauon 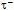 to expose
to expose 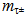 = 1776.84 MeV/c2[39]. Similarly, we think that the 1st generation quarks as ⅔ and ⅓ fractions of the ground-state tori of opposite chirality will adapt to the high densities in energy by adopting the 2nd generation curvature conformations, known as the charm c and strange s quarks, or eventually taking up the 3rd generations paths known as the top t and bottom b quarks. The well-known CKM matrix provides the strengths of flavor-changing weak decays[44,45].
= 1776.84 MeV/c2[39]. Similarly, we think that the 1st generation quarks as ⅔ and ⅓ fractions of the ground-state tori of opposite chirality will adapt to the high densities in energy by adopting the 2nd generation curvature conformations, known as the charm c and strange s quarks, or eventually taking up the 3rd generations paths known as the top t and bottom b quarks. The well-known CKM matrix provides the strengths of flavor-changing weak decays[44,45].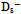 pseudoscalar meson comprising charm and anti-strange quark, i.e., c~s*, in the planar geometry of an opened torus amounts to
pseudoscalar meson comprising charm and anti-strange quark, i.e., c~s*, in the planar geometry of an opened torus amounts to 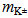 = 1968.47 MeV/c2[39] (Fig. 8). Since
= 1968.47 MeV/c2[39] (Fig. 8). Since 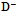 comprising c~d* has a comparable mass
comprising c~d* has a comparable mass 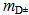 = 1869.60 MeV/c2[39], we deduce that the unpaired 2nd generation loop is responsible for the most of its mass. In contrast due to the partial pairing of the 2nd generation loops at the termini of
= 1869.60 MeV/c2[39], we deduce that the unpaired 2nd generation loop is responsible for the most of its mass. In contrast due to the partial pairing of the 2nd generation loops at the termini of 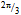 arc the mass
arc the mass 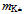 = 493.68 MeV/c2 of kaon
= 493.68 MeV/c2 of kaon 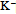 [39], i.e., u~s* is only moderate and comparable to that of
[39], i.e., u~s* is only moderate and comparable to that of 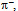 i.e., u~d* (Fig. 7). The contribution of the unpaired 2nd generation loops is particularly pronounced by the high mass
i.e., u~d* (Fig. 7). The contribution of the unpaired 2nd generation loops is particularly pronounced by the high mass 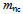 = 2980.30 MeV/c2 of the charmed
= 2980.30 MeV/c2 of the charmed 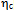 [39] of c~c* composition. Vector mesons in all generations have somewhat higher masses than their pseudo scalar counterparts with the same quark composition. Apparently the phase cancellation of twisted loops in the tetrahedral coordination is impaired further from the planar coordination as is the case also with the 1st generation mesons. Thus, we conclude that the imperfect pairing of quanta in each generation contributes mostly to the mass. For example, the unpaired loops of c and c* of the excited state of charmonium
[39] of c~c* composition. Vector mesons in all generations have somewhat higher masses than their pseudo scalar counterparts with the same quark composition. Apparently the phase cancellation of twisted loops in the tetrahedral coordination is impaired further from the planar coordination as is the case also with the 1st generation mesons. Thus, we conclude that the imperfect pairing of quanta in each generation contributes mostly to the mass. For example, the unpaired loops of c and c* of the excited state of charmonium 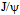 apparently projects considerably onto the surroundings which manifests itself as the high mass
apparently projects considerably onto the surroundings which manifests itself as the high mass 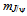 = 3096.92 MeV/c2[39]. The unpaired 3rd generation quanta seem to perturb the vacuum even more. The high mass
= 3096.92 MeV/c2[39]. The unpaired 3rd generation quanta seem to perturb the vacuum even more. The high mass 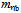 = 9390.9 MeV/c2 of
= 9390.9 MeV/c2 of 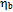 [39] we attribute to the unpaired loops of the b~b* quarks in the toroidal coordination. Conversely we think that the tetrahedral topology of quarks in Y (bottomonium) contribute further to give mY = 9460.30 MeV/c2[39].We expect that in diverse baryons the quarks in three flavors combine in the tetrahedral coordination. Hence the three-quark geodesics will project onto the surroundings much alike the two-quark vector mesons. In other words, the masses of baryons result primarily from the imperfect mutual cancellation of quantum loops in the diverse generations (Fig. 9). For example, we estimate that the mass of
[39] we attribute to the unpaired loops of the b~b* quarks in the toroidal coordination. Conversely we think that the tetrahedral topology of quarks in Y (bottomonium) contribute further to give mY = 9460.30 MeV/c2[39].We expect that in diverse baryons the quarks in three flavors combine in the tetrahedral coordination. Hence the three-quark geodesics will project onto the surroundings much alike the two-quark vector mesons. In other words, the masses of baryons result primarily from the imperfect mutual cancellation of quantum loops in the diverse generations (Fig. 9). For example, we estimate that the mass of 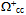 would be about 3650 MeV/c2,
would be about 3650 MeV/c2, 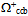 about 7550 and
about 7550 and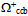 about 8500 MeV/c2.
about 8500 MeV/c2.9. Elementary Dynamics
- Oscillations are familiar from many phenomena occurring at various levels of natural hierarchy. These repeating to-and-fro motions take place between two or more states. Similarly, vector mesons and baryons may roll over from one tetrahedral coordination to the other (Fig. 10). When the tetrahedron flattens toward the transition midpoint, the loops in the adjacent quarks will roll increasingly more out-of-phase, but conversely the arcs of quarks will turn increasingly more co-planar. Hence the transition is broad which is particularly pronounced by the
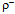 line.Likewise, baryons with angular momentum and parity JP = 1/2+ are readily excited to JP = 3/2+ (Fig. 10). Widths of their resonance lines display breathing from a tetrahedral coordination to another. For example, the characteristic mass
line.Likewise, baryons with angular momentum and parity JP = 1/2+ are readily excited to JP = 3/2+ (Fig. 10). Widths of their resonance lines display breathing from a tetrahedral coordination to another. For example, the characteristic mass 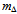 = 1232.1 MeV/c2 of
= 1232.1 MeV/c2 of  resonances has a considerable width
resonances has a considerable width 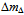 ≈ 118 MeV/c2[39]. We expect baryons when composed of quarks in different generation, to display narrower resonances.
≈ 118 MeV/c2[39]. We expect baryons when composed of quarks in different generation, to display narrower resonances. and
and  or Z bosons. For example, when neutral pseudoscalar mesons K0, i.e., d~s* ↔ d*~s and D0, i.e., c~u* ↔ c*~u oscillate, the quanta in the two quarks of opposite charge and different generation will be first absorbed by a pair of W and W, and then re-emitted by the reversed pair of weak bosons (Fig. 11). The two bosons as open actions serve to invert the path from one chiral consensus to the other. We expect analogous oscillations for b~s* and c~t*. Similarly, the Z boson will mediate the reversal of chirality for two oppositely charged tori, e.g., in a scattering process
or Z bosons. For example, when neutral pseudoscalar mesons K0, i.e., d~s* ↔ d*~s and D0, i.e., c~u* ↔ c*~u oscillate, the quanta in the two quarks of opposite charge and different generation will be first absorbed by a pair of W and W, and then re-emitted by the reversed pair of weak bosons (Fig. 11). The two bosons as open actions serve to invert the path from one chiral consensus to the other. We expect analogous oscillations for b~s* and c~t*. Similarly, the Z boson will mediate the reversal of chirality for two oppositely charged tori, e.g., in a scattering process 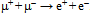 .Various oscillations as well as other stationary dynamics over their characteristic periods, comply with CPT symmetry. However when the system is not at the equilibrium with its surroundings, its oscillatory decay will branch asymmetrically.
.Various oscillations as well as other stationary dynamics over their characteristic periods, comply with CPT symmetry. However when the system is not at the equilibrium with its surroundings, its oscillatory decay will branch asymmetrically.10. Discussion
- The principle of least action is familiar to many as the law that defines trajectories of bodies in diverse potentials and delineates passages of light through stratified mediums[9,17-20,46-48]. Yet some may find it odd that we use the supreme law of nature also to describe elementary particles as actions. The adopted tenet is motivated by words of Johannes Kepler: Where there is matter, there is geometry[49]. The holistic principle of least action in its original form[1] does not specify the realm of applications, but explains various phenomena using the general concept of momentum on a path or equivalently energy over time. Since no change of state will yield less than a quantum of action, i.e. the photon, the logical consequence is the atomistic or monadic tenet that regards everything to be composed of the absolutely least action in some multiples. This view is easily mistaken for a reductionist account of nature – on the contrary – the thermodynamic tenet of the least-time free-energy consumption explains emergence and evolution of systems in interactions with their surroundings[50-52].Some two hundred years ago the atomic composition of chemical substances was just an idea among scholars but today atomic models of compounds are familiar to pupils. In the same way, we regard the photon as the a-tom, i.e. the unbreakable action. It is the basic building block of everything that exists. Indeed the discrete character of nature is reflected in multiplicity at all levels of its hierarchical organization[53]. Admittedly, the proton seems immortal in our hands, but the baryon conservation is at stake when matter and quanta of radiation as stoichiometric reactants are drawn in jaws at galactic centers that jet out leptons and -rays[54-56]. The photon is an apparent ingredient of chemical reactions, but it is the element of any other change of state as well.Our representation of particles as least-action paths may seem at first as an uprising idea, but the atomism, e.g., in the form of luxon theory is nothing novel[57]. Likewise, the torus model of electron appeared early on[36,37] and closed string models have maintained interest ever since[58]. A mere consequence of the torus topology is the presented planar and tetrahedral coordination of quarks in mesons and baryons. The basic geometry implies also how baryons could pack together, e.g., at an atomic nucleus and even tighter as di-mesons and tetra-quarks in a compact star where high density could trigger and sustain annihilation of the opposite chiralities to result in extremely luminous radiation.The actions are real representations of various particles and their transformations are concrete accounts of diverse processes, yet one may question, why these particular paths are found in nature and not some others instead. Likewise, one may ask, why some specific molecules are engaged in processes of life and not some others. However, we hardly wonder, why certain gadgets are employed in economic activities while others have been abandoned – well, we simply keep those that work[59,60]. Accordingly, the supreme law of nature implies that the flows of energy themselves will search and naturally select the paths, i.e. particles and interactions, that will consume free energy in the least time[61] whereas less effective paths will eventually run dry. There is no need for the anthropic principle[62] when there is no demarcation between animate and inanimate[63,64]. There is no room for choices but the constants of nature are consequences of geometry when nature is understood to be embodied in actions.Moreover, the notion of action renders the central concepts of physics, namely space and time, with tangible representations. A coordinate of space embodies a closed circulation of energy, and a moment of time will elapse when the circulation opens up either to acquire or discard quantized flux of energy[32]. The holistic worldview by the principle of least action is neither new nor revolutionary. It stems from the foundations of physics[65] and agrees with observations. Our physical portrayal of particles as actions will disclose that the mass of body depends on how much its energy density on the least-action path perturbs, i.e. projects onto the surrounding actions, the photons which are the generators of the lowest group symmetry. The logic entails that the system of masses characterized by generators of diverse groups SU is incomplete to prove its consistency without reference to its massless complement of U(1)[66]. Since the universal background energy density is in balance with all bodies, the mass m of a body is in relation to all bodies
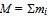 via characteristics of the universal vacuum
via characteristics of the universal vacuum 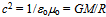 , i.e.
, i.e. 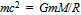 [67]. Thus when the mass of a body is measured, the corresponding geodesic’s curvature will be compared with the universal radius of curvature R due to all bodies. Indeed the mass manifests itself as a curved spacetime. However, the notion of vacuum does not refer to an abstract continuously differentiable mathematical manifold, but to the physical background density embodied by actions among actions. A particle acquires its mass via the inter-actions that propagate the Universe over along the least-time paths. The universal frame of reference is not a conceptual construction of our choice, but the true fabric that couples to any motion. For example, the dipole anisotropy of cosmic background radiation reveals that our galaxy is moving in relation to everything else[68]. The all-around hovering universal energy density that couples everything to everything else parallels Mach’s thinking about inertia. When everything is described in terms of actions, then everything is invariably in relation to everything else. Therefore the curvature and chirality of particular paths invariably relate gravitational and electromagnetic interactions, resembling earlier propositions[69,70], as well as weak and strong interactions with one another. In this sense no fundamental force is more fundamental than any other, but all forces are manifestations of energy differences of various kinds[10].The Universe is not a static setting, but in evolution to attain the stationary state in the “zero-density surroundings” by combustion of diverse forms of bound quanta to freely propagating photons that constitute the vacuum. It seems secondary to us whether the imaginable initial state contained exclusively closed actions or already also high-energy photons in a fluctuating thermodynamic balance with bound quanta, but for the Universe to emerge from nothing would violate conservation of quanta. Early oscillations, whose remnants we detect today[71], were no privilege of the universal evolution, but observed in many other natural process when free energy is large in comparison with bound energy[72]. During the evolution of the Universe, Kepler’s relation R3/T2 = GM serves to equate the change in the rate of expansion dtH = -1/T2, via the gravitational constant G, with the average mass density
[67]. Thus when the mass of a body is measured, the corresponding geodesic’s curvature will be compared with the universal radius of curvature R due to all bodies. Indeed the mass manifests itself as a curved spacetime. However, the notion of vacuum does not refer to an abstract continuously differentiable mathematical manifold, but to the physical background density embodied by actions among actions. A particle acquires its mass via the inter-actions that propagate the Universe over along the least-time paths. The universal frame of reference is not a conceptual construction of our choice, but the true fabric that couples to any motion. For example, the dipole anisotropy of cosmic background radiation reveals that our galaxy is moving in relation to everything else[68]. The all-around hovering universal energy density that couples everything to everything else parallels Mach’s thinking about inertia. When everything is described in terms of actions, then everything is invariably in relation to everything else. Therefore the curvature and chirality of particular paths invariably relate gravitational and electromagnetic interactions, resembling earlier propositions[69,70], as well as weak and strong interactions with one another. In this sense no fundamental force is more fundamental than any other, but all forces are manifestations of energy differences of various kinds[10].The Universe is not a static setting, but in evolution to attain the stationary state in the “zero-density surroundings” by combustion of diverse forms of bound quanta to freely propagating photons that constitute the vacuum. It seems secondary to us whether the imaginable initial state contained exclusively closed actions or already also high-energy photons in a fluctuating thermodynamic balance with bound quanta, but for the Universe to emerge from nothing would violate conservation of quanta. Early oscillations, whose remnants we detect today[71], were no privilege of the universal evolution, but observed in many other natural process when free energy is large in comparison with bound energy[72]. During the evolution of the Universe, Kepler’s relation R3/T2 = GM serves to equate the change in the rate of expansion dtH = -1/T2, via the gravitational constant G, with the average mass density 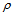 that is still in for combustion to photons. The natural process that manifests itself as the expanding Universe, like any other within it, is expected to follow a sigmoid curve which on a log-log plot is mostly a straight line, but deviates at the beginning and end from the power law[17,27,72,73].The powerful principle of least action in its original open form explains many puzzling phenomena, yet it may fail to meet expectations of many contemporaries. Namely, it does not provide precise predictions. For example, in this study we did not calculate any action, but only proposed few paths in agreement with known properties of particles and characteristics of processes. However, the analysis of the equation of evolution reveals why nature remains unpredictable. A change in action is inherently intractable process when there are alternative pathways to consume free energy. Then flows of energy cannot be separated from their driving forces to solve tracks of future. This non-holonomic and hence non-computable character of nature manifests itself in branching processes that yield the phylogeny of particles and other species as well as in numerous other hard problems[74-77]. The basic paths of quantized actions, such as quarks, merely serve to trace taxonomy of known actions, in the same way as conserved fragments of genomes serve to root a phylogenic tree of species. Thus, rather than insisting on having a predictable nature, e.g., by demanding a theory of physics to comply with unitarity or a gauge group, it is time to recognize the role of history, i.e. the non-holonomic character of nature as the ultimate source of unpredictability.To describe evolution of the Universe as a least-time spontaneous symmetry breaking process from naissance characterized by some high group SU(nsup) toward the heat death characterized by U(1) is a coherent and comprehensive account. Yet, the thermodynamic tenet does not seem to answer the obvious but perhaps ill-posed inquiry about the imaginable initial state, namely, why did the Universe emerge?
that is still in for combustion to photons. The natural process that manifests itself as the expanding Universe, like any other within it, is expected to follow a sigmoid curve which on a log-log plot is mostly a straight line, but deviates at the beginning and end from the power law[17,27,72,73].The powerful principle of least action in its original open form explains many puzzling phenomena, yet it may fail to meet expectations of many contemporaries. Namely, it does not provide precise predictions. For example, in this study we did not calculate any action, but only proposed few paths in agreement with known properties of particles and characteristics of processes. However, the analysis of the equation of evolution reveals why nature remains unpredictable. A change in action is inherently intractable process when there are alternative pathways to consume free energy. Then flows of energy cannot be separated from their driving forces to solve tracks of future. This non-holonomic and hence non-computable character of nature manifests itself in branching processes that yield the phylogeny of particles and other species as well as in numerous other hard problems[74-77]. The basic paths of quantized actions, such as quarks, merely serve to trace taxonomy of known actions, in the same way as conserved fragments of genomes serve to root a phylogenic tree of species. Thus, rather than insisting on having a predictable nature, e.g., by demanding a theory of physics to comply with unitarity or a gauge group, it is time to recognize the role of history, i.e. the non-holonomic character of nature as the ultimate source of unpredictability.To describe evolution of the Universe as a least-time spontaneous symmetry breaking process from naissance characterized by some high group SU(nsup) toward the heat death characterized by U(1) is a coherent and comprehensive account. Yet, the thermodynamic tenet does not seem to answer the obvious but perhaps ill-posed inquiry about the imaginable initial state, namely, why did the Universe emerge?ACKNOWLEDGEMENTS
- Tapio Kulmala, Tapio Salminen, Jouko Seppänen and Avril Styrman for insightful comments and productive discussions.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML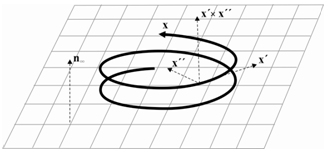
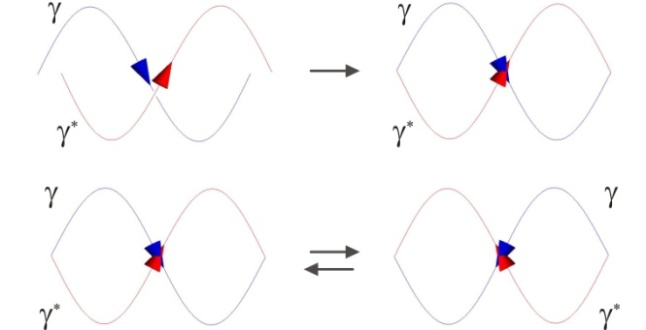
 (blue) is the basic action whose momentum on the path of wavelength is indivisible. (For clarity only the electric component is illustrated.) The opposite polarization corresponds to the antiphoton
(blue) is the basic action whose momentum on the path of wavelength is indivisible. (For clarity only the electric component is illustrated.) The opposite polarization corresponds to the antiphoton  * (red). When
* (red). When  and
and  * co-propagate (as exemplified above), the electromagnetic force will vanish, but the modulus of the compound wave can be regarded as a boson (graviton). These compound bosons will carry energy from dense to sparse loci to level off density differences. In a stationary state the bosons propagate evenly in all opposite directions (below), hence there is no net flow of energy density. Thus also the modulus of the to-and-fro density wave can be regarded as a boson (Higgs) which embodies the standing density of stationary surroundings
* co-propagate (as exemplified above), the electromagnetic force will vanish, but the modulus of the compound wave can be regarded as a boson (graviton). These compound bosons will carry energy from dense to sparse loci to level off density differences. In a stationary state the bosons propagate evenly in all opposite directions (below), hence there is no net flow of energy density. Thus also the modulus of the to-and-fro density wave can be regarded as a boson (Higgs) which embodies the standing density of stationary surroundings
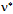 (red) is the complex conjugate, i.e. the sense of circulation is reverse in relation to an observer. The planar circulations would not perturb a perfectly planar surrounding at all. Thus their mass in the universal surroundings of increasingly larger radius is limiting to zero
(red) is the complex conjugate, i.e. the sense of circulation is reverse in relation to an observer. The planar circulations would not perturb a perfectly planar surrounding at all. Thus their mass in the universal surroundings of increasingly larger radius is limiting to zero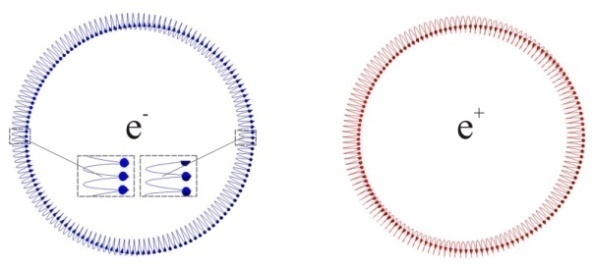
 and magnetic moment
and magnetic moment  . Due to the helical pitch, seen as the roll of arrow heads around the torus, the loops at the opposite phase of the torus (blown up) do not cancel each other perfectly. Therefore the geodesic’s projection on the reference actions constituting the vacuum is not zero which manifests itself as the finite mass me. The anomalous excess in
. Due to the helical pitch, seen as the roll of arrow heads around the torus, the loops at the opposite phase of the torus (blown up) do not cancel each other perfectly. Therefore the geodesic’s projection on the reference actions constituting the vacuum is not zero which manifests itself as the finite mass me. The anomalous excess in  stems from the “excess” path length that accumulates from the roll around the torus. Likewise, the quantized flow of energy on the toroidal geodesic of opposite handedness (red) constitutes the positron
stems from the “excess” path length that accumulates from the roll around the torus. Likewise, the quantized flow of energy on the toroidal geodesic of opposite handedness (red) constitutes the positron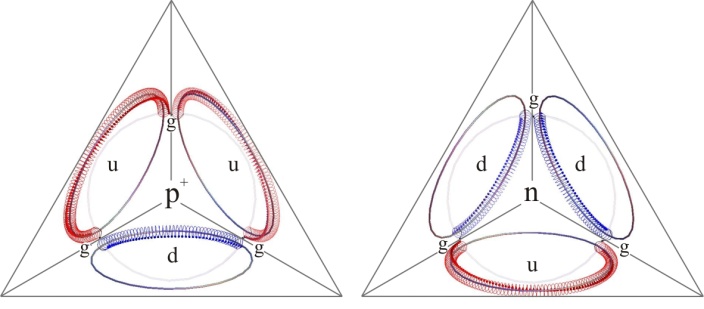
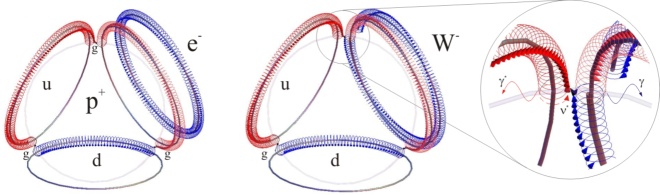
 . The resulting excised torus is W- which will consume the adjacent u-quark in annihilation so that the remaining 1/3 residual of W- when closing with neutrino, will become the d-quark that completes the re-closure as uud, the neutron n
. The resulting excised torus is W- which will consume the adjacent u-quark in annihilation so that the remaining 1/3 residual of W- when closing with neutrino, will become the d-quark that completes the re-closure as uud, the neutron n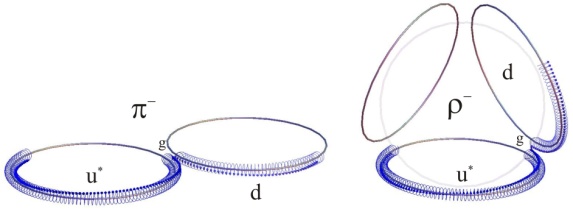
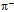 and
and 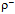 Most of
Most of 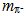 stems from the quanta that are along the two non-opposing
stems from the quanta that are along the two non-opposing 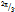 -arcs since they fail to pair perfectly with each other due to the accrued phases. The self-interference of quanta in the tetrahedral coordination of u and d* quarks is impaired even more which will manifest itself as the high mass
-arcs since they fail to pair perfectly with each other due to the accrued phases. The self-interference of quanta in the tetrahedral coordination of u and d* quarks is impaired even more which will manifest itself as the high mass 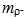
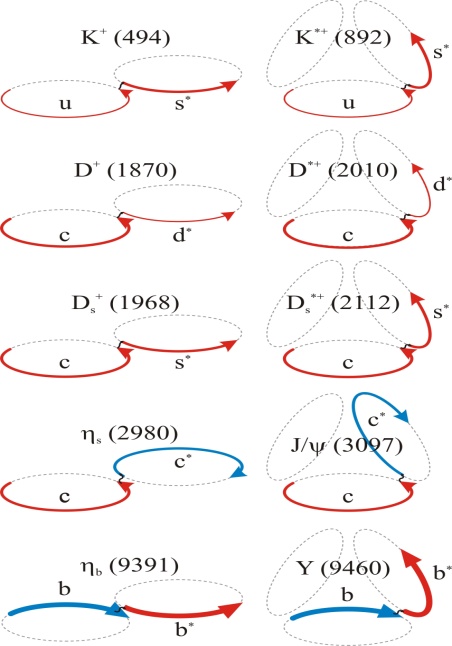
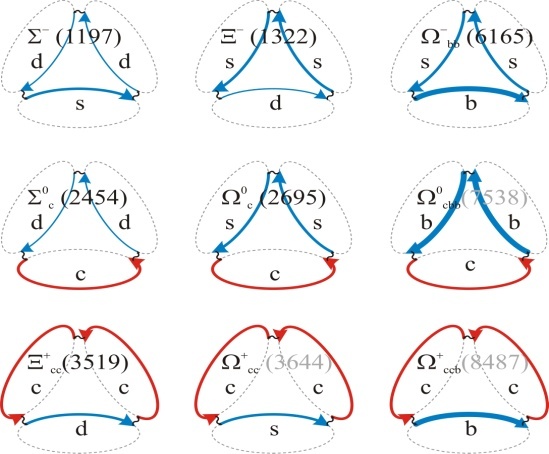
 (1232 MeV/c2) of uuu quark composition
(1232 MeV/c2) of uuu quark composition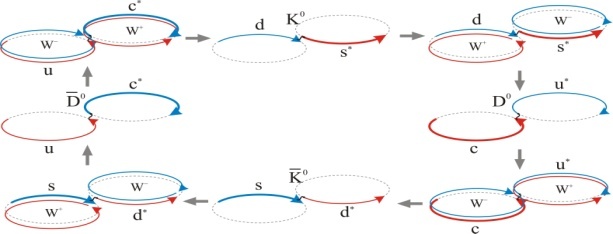
 and
and  (depicted as cut rings)
(depicted as cut rings)