-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2012; 2(4): 61-66
doi: 10.5923/j.ijtmp.20120204.02
Fluctuations of the Metric Tensor: On Fermion Propagators and on the Cosmological Constant
Alex H. Blin
CFC, Departamento de F´ısica, Universidade de Coimbra, P-3004-516 Coimbra, Portugal
Correspondence to: Alex H. Blin , CFC, Departamento de F´ısica, Universidade de Coimbra, P-3004-516 Coimbra, Portugal.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Conformal fluctuations of the metric tensor are considered. They give rise to a Planck scale size lower bound of the proper length. Infinities arising from the point-like character of particles are thus avoided, expressions related to fermion propagators are finite without the need to renormalize or regularize. The quark condensate, constituent quark mass, pion mass, and pion weak decay constant are calculated within the SU(2) Nambu--Jona-Lasinio model. The numerical values are consistent with known strong interaction physics if one assumes very small values of the current quark mass and effective coupling constant. The usual values of these quantities in hadron phenomenology can be interpreted as resulting from dressing of the very small bare quantities with the fluctuations. With respect to the cosmological constant it is shown that a cosmological constant term, which may initially exist in the gravitational action, is ”masked” by the fluctuations of the metric, i.e., it does not appear in the final Einstein equation. Instead, the fluctuations give rise to a cosmological constant themselves.
Keywords: Metric Tensor, Quark Propagators, Effective Lagrangian, Renormalization, Cosmological Constant
Article Outline
1. Introduction
- The concept of a particle in quantum field theory is point- like. This fact leads to the known divergent expressions which are usually tackled by renormalization or regularization techniques. Quantum gravity, however, introduces a coarse graining of spacetime at the Planck scale. In the present work an effective description of spacetime fluctuations is proposed. On the microscopic scale, of interest in quantum field theory, the resulting fuzziness of spacetime is shown to render usually divergent expressions finite, without the need for renormalization or regularization. On a macroscopic scale, the fluctuations affect the behavior of the cosmological constant.The coarse graining of spacetime indicates that the metric tensor has to be considered a quantum variable. The idea that quantum fluctuations of the metric can have the effect of a regulator is not new, see for instance[1] and references therein, and[2,3]. The expected effect is that propagators should be “smeared out”[4]. In order to preserve the light cone structure, a necessary condition for not violating causality at any instant of the variation of the metric, only con- formal fluctuations[5] are studied here. The averaging over these fluctuations results in a fuzziness of the light cone at the level of the Planck scale. A full theory of quantum gravity is expected to require more than the quantization of the conformal mode. Issuesrelated to gauge-fixing and the isolation of the relevant degrees of freedom are not addressed here. The conformal mode should nevertheless reflect the basic features of the effect of quantum gravity on the observables under consideration. Due to the conformality and the fact that the field representing the fluctuations is treated in lowest order, i.e. in classical approximation when deriving Einstein’s equation from variation of the action, the present procedure is in this sense not fundamental but should be regarded as an effective approach.The fluctuations give rise to a lower bound of the proper length, as should be expected also on heuristic grounds. Thus the infinities mentioned above are avoided without the need for regularization. The consequences for several physical quantities related to Green’s functions are studied in the context of the Nambu--Jona-Lasinio model[6,7] using standard techniques[8-11], adapted to the case at hand. The intention here is to check the consistency of the values, with the implicit assumption that the quarks do behave point-like down to the Planck scale (but not beyond that point), and that strong interactions do not introduce another (much larger) regularization scale.An additional consequence of fluctuations of the metric is the emergence of a cosmological constant[12,13], like in other theories with scalar fields coupled to the metric (see e.g.[14] and references therein). This cosmological constant is independent of the one conjectured from vacuum fluctuations of quantum field theory (QFT), which pose the well-known 120 orders of magnitude problem[15]. It is shown that in the present approach this problem is of no relevance due to a cancellation of terms in Einstein’s equation.The following section introduces the scalar field which represents the fluctuations of the metric, and it is shown how they impose a lower bound on the proper length. Section 3 discusses fermion propagation in curved spacetime. In section 4 the formal expressions for the quark condensate and the quark mass are calculated, followed by the expressions for the pion mass and weak decay constant in section 5. Section 6 is devoted to the cosmological constant which arises from the fluctuations of the metric. Numerical results and a discussion are presented in the final section.
2. Conformal Fluctuations of the Metric
- This section summarizes and adapts some known results (see [5] for instance). The starting point of the present approach is a scalar field
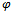 which is to represent the quantum fluctuations of the generalized metric
which is to represent the quantum fluctuations of the generalized metric 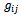 about its “classical” or “background” value
about its “classical” or “background” value . All “background” quantities and operators are denoted by overbars. In the sign convention applied here the Ricci tensor is calculated by the contraction
. All “background” quantities and operators are denoted by overbars. In the sign convention applied here the Ricci tensor is calculated by the contraction  and all spacetime indices, Latin or Greek, run from 0 to 3, with the signature (+ - - -). A large part of the following discussion assumes flat background spacetime, so
and all spacetime indices, Latin or Greek, run from 0 to 3, with the signature (+ - - -). A large part of the following discussion assumes flat background spacetime, so 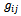 = ηij = diag(1, −1, −1, −1), except for the section on the cosmological constant, as in cosmology
= ηij = diag(1, −1, −1, −1), except for the section on the cosmological constant, as in cosmology 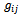 is usually the Friedman-Lemaˆıtre-Robertson-Walker metric, although this fact is not used explicitly. In most expressions, natural units with ħ = c = 1 are used.The simplest kind of metric variation is
is usually the Friedman-Lemaˆıtre-Robertson-Walker metric, although this fact is not used explicitly. In most expressions, natural units with ħ = c = 1 are used.The simplest kind of metric variation is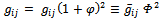 | (1) |
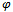 (x) is a scalar field representing the quantum fluctuations of the metric about the classical value. The fluctuation average (vacuum expectation value) is required to be <
(x) is a scalar field representing the quantum fluctuations of the metric about the classical value. The fluctuation average (vacuum expectation value) is required to be <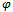 > = <
> = < ,m> = 0 (the comma denotes partial derivative), meaning that the center of the fluctuations is the classical value and that there is no drift of
,m> = 0 (the comma denotes partial derivative), meaning that the center of the fluctuations is the classical value and that there is no drift of  in spacetime, a fact consistent with energy conservation[13]. The field
in spacetime, a fact consistent with energy conservation[13]. The field 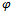 represents an additional, conformal degree of freedom.The full metric
represents an additional, conformal degree of freedom.The full metric 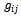 is now inserted into the Hilbert action of General Relativity
is now inserted into the Hilbert action of General Relativity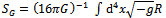 | (2) |
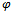 the total scalar curvature is
the total scalar curvature is 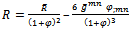 | (3) |
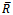 denotes the classical background scalar curvature, i.e. the usual one without fluctuations, and the semicolon denotes covariant derivative. In the special case of flat background spacetime (
denotes the classical background scalar curvature, i.e. the usual one without fluctuations, and the semicolon denotes covariant derivative. In the special case of flat background spacetime (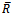 =0) which is studied next, the action reduces to
=0) which is studied next, the action reduces to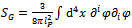 | (4) |
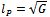 (in natural units), G being the gravitational constant. (The sign convention differs from the one used in an earlier version of this work [16]). Note that the resulting action is proportional to the usual scalar action, with the additional factor
(in natural units), G being the gravitational constant. (The sign convention differs from the one used in an earlier version of this work [16]). Note that the resulting action is proportional to the usual scalar action, with the additional factor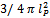 .The vacuum expectation value of the line element becomes
.The vacuum expectation value of the line element becomes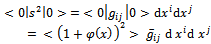 | (5) |
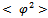 is calculated formally as the limit
is calculated formally as the limit 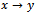 of the scalar propagator [17] but with the additional factor mentioned above appropriately included [5]:
of the scalar propagator [17] but with the additional factor mentioned above appropriately included [5]: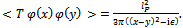 | (6) |
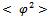 diverges as
diverges as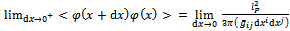 | (7) |
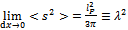 | (8) |
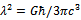 , written here in its full form, will appear frequently in the following expressions). This means that the fluctuations of the metric impose a lower bound on the proper length. Any point-like object is "smeared out" at the level of the Planck length. Infinities arising from the point-like character of particles are thus avoided. Moreover, due to the presence of the fluctuations, the classical squared distance
, written here in its full form, will appear frequently in the following expressions). This means that the fluctuations of the metric impose a lower bound on the proper length. Any point-like object is "smeared out" at the level of the Planck length. Infinities arising from the point-like character of particles are thus avoided. Moreover, due to the presence of the fluctuations, the classical squared distance  is replaced by
is replaced by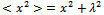 | (9) |
3. Fermions in Curved Spacetime
- When dealing with fermion propagators one has to take into account that any deviation of the metric from Minkowski spacetime
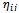 alters the Dirac equation. Its general form is [18,19]
alters the Dirac equation. Its general form is [18,19]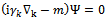 | (10) |
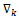 is the covariant derivative of a spinor,
is the covariant derivative of a spinor,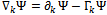 | (11) |
 are obtained from the relation
are obtained from the relation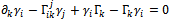 | (12) |
 | (13) |
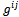 and where the
and where the 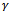 matrices are related to the flat spacetime
matrices are related to the flat spacetime 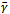 matrices by
matrices by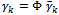 | (14) |
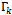 from (12). Inserting them back into the covariant derivative, the Dirac equation can be written for the case at hand as
from (12). Inserting them back into the covariant derivative, the Dirac equation can be written for the case at hand as 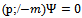 | (15) |
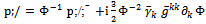 | (16) |
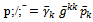 and
and 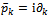
4. Quark Condensate and Quark Mass
- Passing now to the discussion of quantities containing a single fermion propagator, the quark condensate is known to be related to the fermion propagator by
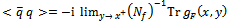 | (17) |
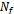 is the number of flavors and Tr stands for the trace in flavor, color and Dirac spaces. The spacetime dependent propagator
is the number of flavors and Tr stands for the trace in flavor, color and Dirac spaces. The spacetime dependent propagator 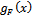 is obtained from its four-momentum dependent counterpart
is obtained from its four-momentum dependent counterpart  by a Fourier transform. The condensate becomes
by a Fourier transform. The condensate becomes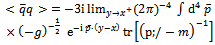 | (18) |
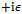 term has been omitted from the denominator, for simplicity of notation. Also implicit is the evaluation of the vacuum expectation value of the fluctuations. The momentum
term has been omitted from the denominator, for simplicity of notation. Also implicit is the evaluation of the vacuum expectation value of the fluctuations. The momentum 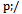 is the full one (16), and g refers to the determinant of the metric tensor
is the full one (16), and g refers to the determinant of the metric tensor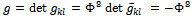 | (19) |
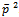 . After some algebra one has
. After some algebra one has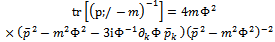 | (20) |
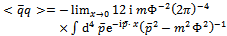 | (21) |
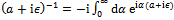 (remembering the presence of the term
(remembering the presence of the term 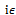 in the denominator), the
in the denominator), the 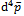 -integration can be performed,
-integration can be performed,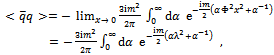 | (22) |
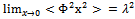 | (23) |
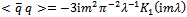 | (24) |
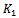 being the modified Bessel function. In the small argument limit
being the modified Bessel function. In the small argument limit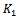 , behaves as the inverse of the argument, so one finally gets
, behaves as the inverse of the argument, so one finally gets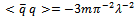 | (25) |
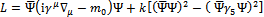 | (26) |
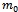 is the current quark mass and
is the current quark mass and 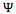 is the quark field. As one can see, the quark fields are the only degrees of freedom in this model, the information on the gluons is residing in the constant k . It has been shown in[20] that this type of lagrangian can be obtained from QCD by integrating out the gluonic degrees of freedom. It is reasonable to expect that gluonic degrees of freedom are unimportant at "high energy" where we know that quarks are asymptotically free. But how high is "high energy"? Asymptotic freedom is observed in QCD where energy scales are measured in terms of GeV, but since in this work energies up to the Planck energy are considered, there is no guarantee that the present type of lagrangian can still be used, the gluons could become important again. Let me simply assume here the validity of this lagrangian down to the Planck scale and use it to study the consequences of the fluctuations, remembering the words of caution about its applicability. After Fierz symmetrization in color, flavor and Dirac spaces the lagrangian acquires more terms which are not written explicitly here, since they do not contribute to the quantities to be studied. The coupling constant is redefined by the presence of the exchange terms. Let me call this redefined value again k .Note that the model is non-renormalizable and is normally defined only together with some regularization procedure, for instance by using a cut-off typically in the order of 1 GeV, the strong interaction scale. In the present consideration there is no need to regularize, since the results stay finite. The "regularization" arises naturally from the fluctuations at the Planck scale.Some comments are in order regarding the
is the quark field. As one can see, the quark fields are the only degrees of freedom in this model, the information on the gluons is residing in the constant k . It has been shown in[20] that this type of lagrangian can be obtained from QCD by integrating out the gluonic degrees of freedom. It is reasonable to expect that gluonic degrees of freedom are unimportant at "high energy" where we know that quarks are asymptotically free. But how high is "high energy"? Asymptotic freedom is observed in QCD where energy scales are measured in terms of GeV, but since in this work energies up to the Planck energy are considered, there is no guarantee that the present type of lagrangian can still be used, the gluons could become important again. Let me simply assume here the validity of this lagrangian down to the Planck scale and use it to study the consequences of the fluctuations, remembering the words of caution about its applicability. After Fierz symmetrization in color, flavor and Dirac spaces the lagrangian acquires more terms which are not written explicitly here, since they do not contribute to the quantities to be studied. The coupling constant is redefined by the presence of the exchange terms. Let me call this redefined value again k .Note that the model is non-renormalizable and is normally defined only together with some regularization procedure, for instance by using a cut-off typically in the order of 1 GeV, the strong interaction scale. In the present consideration there is no need to regularize, since the results stay finite. The "regularization" arises naturally from the fluctuations at the Planck scale.Some comments are in order regarding the 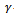 -matrices appearing in this kind of quartic interaction lagrangian. The expression of the pseudoscalar-isovector term
-matrices appearing in this kind of quartic interaction lagrangian. The expression of the pseudoscalar-isovector term 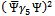 stands actually for
stands actually for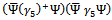 . Since
. Since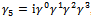 , it carries the inverse fourth power of
, it carries the inverse fourth power of 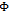 :
: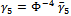 | (27) |
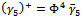 | (28) |
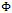 cancel in the lagrangian. (The same holds true for terms containing
cancel in the lagrangian. (The same holds true for terms containing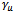 ). It should be noted also that
). It should be noted also that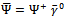 | (29) |
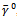 , in order to be compatible with current conservation
, in order to be compatible with current conservation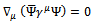 | (30) |
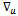 being again the covariant derivative.In principle, all the terms appearing in the Fierz symmetric lagrangian have to be considered in the evaluation of the constituent mass. As in the flat spacetime case, however, only the scalar term
being again the covariant derivative.In principle, all the terms appearing in the Fierz symmetric lagrangian have to be considered in the evaluation of the constituent mass. As in the flat spacetime case, however, only the scalar term 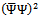 contributes, essentially since
contributes, essentially since 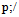 has the same
has the same 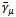 -structure as
-structure as 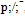 , which cancels the contributions in the traces in the same way as in flat spacetime without fluctuations, with the exception of the vector term
, which cancels the contributions in the traces in the same way as in flat spacetime without fluctuations, with the exception of the vector term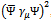 , see below. The constituent mass m is related to the current mass
, see below. The constituent mass m is related to the current mass 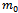 via the self-energy
via the self-energy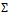 :
: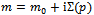 | (31) |
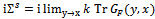 | (32) |
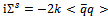 | (33) |
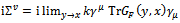 | (34) |
 , so the first term vanishes right away since it is odd in
, so the first term vanishes right away since it is odd in 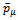 in the integral, and the second because it is odd in the quantum fluctuations. Therefore, using (25), the constituent quark mass is obtained from
in the integral, and the second because it is odd in the quantum fluctuations. Therefore, using (25), the constituent quark mass is obtained from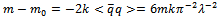 | (35) |
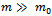 :
: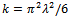 | (36) |
5. Pion Mass and Weak Decay Constant
- As an example for expressions containing two fermion propagators, consider now the pion in the Nambu--Jona- Lasinio model. The vertex involving the pion is written in terms of quarks as
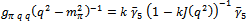 | (37) |
 | (38) |
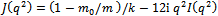 | (39) |
 | (40) |
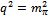 , the quark loop integral obeys
, the quark loop integral obeys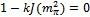 , as seen in (37), and the pion mass can be deduced from
, as seen in (37), and the pion mass can be deduced from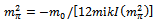 | (41) |
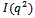 can be further rewritten using the convolution theorem as
can be further rewritten using the convolution theorem as | (42) |
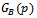 and
and 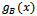 being of the form of boson propagators in momentum and coordinate space. Due to the vacuum expectation value of the fluctuations,
being of the form of boson propagators in momentum and coordinate space. Due to the vacuum expectation value of the fluctuations, 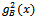 becomes
becomes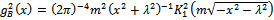 | (43) |
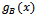 and using (42), one gets
and using (42), one gets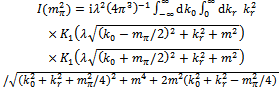 | (44) |
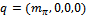 .It is worthwhile noting that, since integrals are finite in the present scheme, it is allowed to shift variables without introducing ambiguities, contrary to the usual case of the infinite integrals appearing in normalization or regularization procedures.The pion weak decay constant
.It is worthwhile noting that, since integrals are finite in the present scheme, it is allowed to shift variables without introducing ambiguities, contrary to the usual case of the infinite integrals appearing in normalization or regularization procedures.The pion weak decay constant 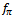 in the chiral limit is written as
in the chiral limit is written as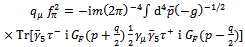 | (45) |
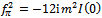 | (46) |
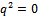 , the integral
, the integral 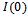 has spherical 4-symmetry and reduces to
has spherical 4-symmetry and reduces to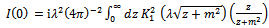 | (47) |
6. The Cosmological Constant
- The Casimir effect is usually considered to be a proof for the existence of the quantum fluctuations of the vacuum required by QFT. Considering them as "real" in the sense of contributing to the energy density of the universe leads to the well-known problem of a cosmological constant 120 orders of magnitude bigger [15] than the one indeed observed [21]. What could be the impact of the metric fluctuations? The procedure to obtain the cosmological constant from the total action
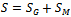 is described in [13], where the gravitational action
is described in [13], where the gravitational action 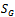 did not contain a cosmological constant from the outset, and
did not contain a cosmological constant from the outset, and 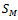 is the matter part in dust approximation. Here, the same procedure is followed, but starting instead from the action
is the matter part in dust approximation. Here, the same procedure is followed, but starting instead from the action 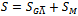 , where
, where | (48) |
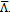 , for instance created by quantum fluctuations of the vacuum.The variation of the action leading to Einstein's equation includes two parts, the variation of the background metric and the variation of the field describing the fluctuations:
, for instance created by quantum fluctuations of the vacuum.The variation of the action leading to Einstein's equation includes two parts, the variation of the background metric and the variation of the field describing the fluctuations: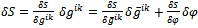 | (49) |
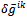 ,
,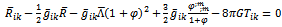 | (50) |
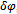 ,
,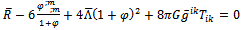 | (51) |
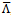 , but when the second equation is used to eliminate the
, but when the second equation is used to eliminate the 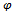 -dependence from the first, the new terms cancel exactly. The resulting Einstein equation is identical to the one previously obtained without the prior
-dependence from the first, the new terms cancel exactly. The resulting Einstein equation is identical to the one previously obtained without the prior 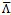 -term. It can again be cast in the form of an Einstein equation
-term. It can again be cast in the form of an Einstein equation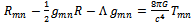 | (52) |
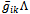 in which
in which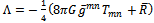 | (53) |
 in the generalized metric and not of the prior
in the generalized metric and not of the prior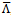 . The contributions of the QFT vacuum fluctuations (if that was the assumed origin of the term
. The contributions of the QFT vacuum fluctuations (if that was the assumed origin of the term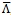 ) cancel in the present approach. The situation is reminiscent of the explanation of the Casimir effect put forward in [22], which does not prove nor require the existence of QFT vacuum fluctuations.
) cancel in the present approach. The situation is reminiscent of the explanation of the Casimir effect put forward in [22], which does not prove nor require the existence of QFT vacuum fluctuations.7. Numerical Results and Discussion
- Neither the pion weak decay constant nor the quark condensate contain the effective coupling constant k explicitly. In this way, these quantities are model independent, as long as one regards the quarks as the only degrees of freedom. Both quantities are dependent indirectly on k via the constituent quark mass. In order to be able to reproduce the experimental value of the pion weak decay constant
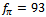 MeV, it is necessary to assume a rather small constituent mass
MeV, it is necessary to assume a rather small constituent mass 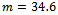 MeV. With the more acceptable value
MeV. With the more acceptable value 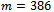 MeV, the decay constant becomes
MeV, the decay constant becomes 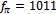 MeV. The discrepancy may be due to the fact that expression (45) is an approximation in the chiral limit. It is interesting to realize that
MeV. The discrepancy may be due to the fact that expression (45) is an approximation in the chiral limit. It is interesting to realize that 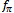 is only logarithmically dependent on the regularization point. Using the Planck length
is only logarithmically dependent on the regularization point. Using the Planck length 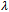 as the covariant cutoff in [8] yields very similar results.The quark condensate, although finite, evaluates to the unusually large value
as the covariant cutoff in [8] yields very similar results.The quark condensate, although finite, evaluates to the unusually large value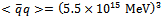 , for the choice
, for the choice 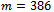 MeV. As discussed for instance in [8], the quark condensate is not renormalization invariant, but
MeV. As discussed for instance in [8], the quark condensate is not renormalization invariant, but 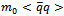 is. In fact, the Gell-Mann--Oakes--Renner relation
is. In fact, the Gell-Mann--Oakes--Renner relation 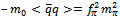 indicates that the current quark mass must be very small in the present situation, of the order of
indicates that the current quark mass must be very small in the present situation, of the order of 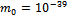 MeV, instead of the usual few MeV. We can imagine that the "bare" current quark mass, appearing in the lagrangian, is successively dressed by the fluctuations of the metric to the few MeV current quark mass usually encountered in hadron physics, and then by the strong interaction, to finally yield the constituent quark mass m . This is seen in (35), where both the Planck length
MeV, instead of the usual few MeV. We can imagine that the "bare" current quark mass, appearing in the lagrangian, is successively dressed by the fluctuations of the metric to the few MeV current quark mass usually encountered in hadron physics, and then by the strong interaction, to finally yield the constituent quark mass m . This is seen in (35), where both the Planck length 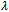 and the effective coupling k enter. To be compatible with (35), the coupling must be very small,
and the effective coupling k enter. To be compatible with (35), the coupling must be very small, 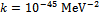 from (36). This can also be imagined as the bare value which is then dressed by the fluctuations to give the more usual order of magnitude in the combinations
from (36). This can also be imagined as the bare value which is then dressed by the fluctuations to give the more usual order of magnitude in the combinations 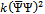 etc. appearing in the lagrangian.Turning next to the pion mass
etc. appearing in the lagrangian.Turning next to the pion mass 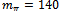 MeV, one finds that (41) is satisfied with the choices
MeV, one finds that (41) is satisfied with the choices 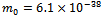 MeV for
MeV for 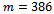 MeV, and
MeV, and 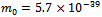 MeV for
MeV for 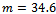 MeV, respectively. Again, the smaller constituent mass seems to be preferred, as it compares well with the Gell-Mann--Oakes--Renner result. One should, however, not attribute too much value to this statement, since the model lagrangian used has to be taken with caution when approaching the Planck scale. As mentioned earlier, gluonic degrees of freedom may become increasingly important at very high energies again, since it is not clear if asymptotic freedom holds up to the Planck energy. It may not be allowed to simply use an effective coupling constant to represent strong interactions close to the Planck energy. The next step along this line of investigation will be to consider a model lagrangian with gluonic degrees of freedom to assess their importance close to the Planck scale and to see whether the results presented here suffer significant changes.No numerical results are discussed with regard to the cosmological constant, as this is done in[13] and the intention here is to show what the effect of the fluctuations of the metric is on a prior presence of a cosmological constant in the action. The contribution of the prior term vanishes, but the metric fluctuations generate a cosmological constant themselves. This is a new and unexpected result. Work is in progress to evaluate whether the prior term cancels only in the dust approximation used here or also under more general conditions.To summarize the results, no essential contradictions have been found in the present scheme, in which conformal quantum fluctuations of the metric tensor introduce a fuzziness of point-like particles at the scale of the Planck length. This fact avoids infinities without the need for renormalization or regularization. The physical values of quantities like the pion mass, pion weak decay constant and constituent quark mass attain reasonable values, if one assumes nonstandard (very small) values of the "bare" current quark mass and effective strong coupling constant. The standard values of the current quark mass and of the coupling constant can be interpreted as resulting from dressing of the bare quantities with the fluctuations of the metric, in a similar way as the constituent mass is obtained by dressing of the usual current quark mass with strong interactions.In the context of the Einstein equation, the fluctuations mask any prior cosmological constant present in the gravitational action. This is an interesting and novel result worth being pursued further.
MeV, respectively. Again, the smaller constituent mass seems to be preferred, as it compares well with the Gell-Mann--Oakes--Renner result. One should, however, not attribute too much value to this statement, since the model lagrangian used has to be taken with caution when approaching the Planck scale. As mentioned earlier, gluonic degrees of freedom may become increasingly important at very high energies again, since it is not clear if asymptotic freedom holds up to the Planck energy. It may not be allowed to simply use an effective coupling constant to represent strong interactions close to the Planck energy. The next step along this line of investigation will be to consider a model lagrangian with gluonic degrees of freedom to assess their importance close to the Planck scale and to see whether the results presented here suffer significant changes.No numerical results are discussed with regard to the cosmological constant, as this is done in[13] and the intention here is to show what the effect of the fluctuations of the metric is on a prior presence of a cosmological constant in the action. The contribution of the prior term vanishes, but the metric fluctuations generate a cosmological constant themselves. This is a new and unexpected result. Work is in progress to evaluate whether the prior term cancels only in the dust approximation used here or also under more general conditions.To summarize the results, no essential contradictions have been found in the present scheme, in which conformal quantum fluctuations of the metric tensor introduce a fuzziness of point-like particles at the scale of the Planck length. This fact avoids infinities without the need for renormalization or regularization. The physical values of quantities like the pion mass, pion weak decay constant and constituent quark mass attain reasonable values, if one assumes nonstandard (very small) values of the "bare" current quark mass and effective strong coupling constant. The standard values of the current quark mass and of the coupling constant can be interpreted as resulting from dressing of the bare quantities with the fluctuations of the metric, in a similar way as the constituent mass is obtained by dressing of the usual current quark mass with strong interactions.In the context of the Einstein equation, the fluctuations mask any prior cosmological constant present in the gravitational action. This is an interesting and novel result worth being pursued further.ACKNOWLEDGEMENTS
- I gratefully acknowledge discussions with E. van Beveren, J.L.A. Fernandes, B. Hiller and J. Hüfner. This work was supported by CERN, 7th Framework and FCT, grant numbers QCDnet 227431, CERN/FP/116334/2010 and HadronPhysics3 283286.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML