Edward H. Jimenez 1, 2
1LaMUSE, Laboratoire de Mathématiques de l'Université de Saint-Étienne, France
2Research and Development Department, EPPetroecuador, Quito, Ecuador
Correspondence to: Edward H. Jimenez , LaMUSE, Laboratoire de Mathématiques de l'Université de Saint-Étienne, France.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Quantum Mechanic axioms are the result of the microscopic cooperative equilibrium among symmetric players (quantum object and human subject). On the other hand, we introduce Nash’s equilibrium in Hilbert space, which has two characteristics: it is a fixed point and it maximizes a utility function. Moreover, evolution and selfadjoint operators have interesting properties which allow us to study steady state in Evolutionary Game Theory. Also, we present cooperative games in complex systems language.The concept of cooperation is important in game theory but is somewhat subtle. The term cooperate means to act together, with a common purpose. Incentive compatibility is equivalent to synergy principle, which appears naturally (to add or to multiply utilities, ec[34]). Finally, wein the relevant results not only proved the main theorems of Quantum Mechanics, Quantum Chemistry and its applications to salt-water but also we resolved some main questions such us: Do hydrogen-bonded networks, in which tunneling plays an important role, exist?, How cooperation and entropy affect water cluster equilibria?. Can salt (ClNa) play an Nobel role in photo-catalysis?. The answers are: tunnel effect it is possible in salt water but not in water, because ClNa, visible light or electricity incentive to produce catalysis or photo-catalysis. Also, If hydrogen-bonded networks and water cluster size increases complexity of an global equilibrium, then tunnel effect appears as an local equilibrium.
Keywords:
Econophysics, Optimal Principle, Cooperation, Nash Equilibrium, Hilbertspace, Evolution Operator, Tunnel Effect
1. Introduction
We will use a systemic perspective which is authorized by research methodology of complex systems[2],[3], in order to present a vision that integrates quantum computing concepts[7] and game theory elements to study cooperative games. The angular stone that unifies these two approaches is classic information theory. However, there is a narrow and formal bridge to carry out these tasks denominated quantum probability. More easily, we can understand quantum probability as the Hilbert space of random variables with finite second moment, see[13],[16].First, approaches related to cooperation appear. After that we carry out a revision of existent literature, such us communication, correlation, entanglement, dependence and common objectives, see[12]. Cooperative game theory enriched by Nash´s product focus approaches common objective topic (resolution of common problems) using bargaining roads which allow us to discover and implement equilibria. Concepts such us correlation, entanglement and dependence are complementary and they are strongly related intuitively. Consequently, we will establish its limits and functional dependences. Finally,[1] and[14] show that coordination and communication concepts can replace correlation (entanglement or dependence), see[5].Second, this work is an example how the analyses of game theory can explain the paradox ofEinstein-Podolski-Rosen (hereafter: ERP) satisfactorily. Nevertheless, Anton Zeilinger, an outstanding researcher in quantum computing, has already expressed that interaction between two particles inentanglement does not have theoretical repercussions in Einstein´s relativity theory, see[4],[6].Third, the main theorems of this paper allow us to obtain Nash’s equilibrium in Hilbert space, which has two properties: it is a fixed point and maximizes a utility function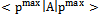 where
where . InHilbert spaces, the norm of a selfadjoint operator (utility matrix: A) permits us to obtain the fixed points
. InHilbert spaces, the norm of a selfadjoint operator (utility matrix: A) permits us to obtain the fixed points , where
, where . A symmetrical matrix is a peculiar case of a selfadjoint operator, which has the advantage of being very usefull in bimatrix symmetrical games. A selfadjoint operator allows us to introduce utilities
. A symmetrical matrix is a peculiar case of a selfadjoint operator, which has the advantage of being very usefull in bimatrix symmetrical games. A selfadjoint operator allows us to introduce utilities 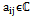 defined on complex numbers.To sum up, Quantum Mechanic axioms are the result of the microscopic cooperative equilibrium among symmetrical players (quantum-object and human-subject). Also, properties of selfadjoint and evolution operators here proved, can be applied to two-player symmetric games. Moreover, this work is an application of econophysics in Quantum Mechanics, see[8],[9].This paper is organized as follows. The first section is a revision of the existent literature about cooperation, entanglement and the Hilbert space of random variables. In the second section, we show the main theorems of complex games and its relationship with entanglement and ERP paradox.In the third section we can see Nash’s equilibrium in Hilbert spaces, evolution operator and steady state. The fourth section is the conclusion of this research.
defined on complex numbers.To sum up, Quantum Mechanic axioms are the result of the microscopic cooperative equilibrium among symmetrical players (quantum-object and human-subject). Also, properties of selfadjoint and evolution operators here proved, can be applied to two-player symmetric games. Moreover, this work is an application of econophysics in Quantum Mechanics, see[8],[9].This paper is organized as follows. The first section is a revision of the existent literature about cooperation, entanglement and the Hilbert space of random variables. In the second section, we show the main theorems of complex games and its relationship with entanglement and ERP paradox.In the third section we can see Nash’s equilibrium in Hilbert spaces, evolution operator and steady state. The fourth section is the conclusion of this research.
2. Cooperation in Economics and Quantum Mechanics
We can denote any strategic-form game Гas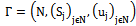 , where N is the set of players,
, where N is the set of players, 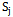 is the set of strategies for player j; and
is the set of strategies for player j; and  is the utility payoff for player j. Here
is the utility payoff for player j. Here  denotes the set of all possible combinations or profiles of strategies that may be chosen by the various players.In general, a randomized strategy is any probability distribution over a set of strategies. We may denote such a randomized strategy in general by
denotes the set of all possible combinations or profiles of strategies that may be chosen by the various players.In general, a randomized strategy is any probability distribution over a set of strategies. We may denote such a randomized strategy in general by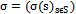 , where
, where 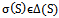 represents the probability of choosing s,
represents the probability of choosing s, 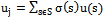 ,
, 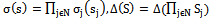 in correlated strategies and
in correlated strategies and  , in non-correlated strategies. Note that in general
, in non-correlated strategies. Note that in general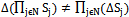 .The concept of cooperation is important in game theory but is somewhat subtle. The term cooperate means "to act together, with a common purpose".The common purpose can be explicit, when players add or multiply energy or utility (synergy principle). Complex game theorem shows us that if we cooperate (to add or to multiply utility), then the results are correlated strategies and actions in order to maximize
.The concept of cooperation is important in game theory but is somewhat subtle. The term cooperate means "to act together, with a common purpose".The common purpose can be explicit, when players add or multiply energy or utility (synergy principle). Complex game theorem shows us that if we cooperate (to add or to multiply utility), then the results are correlated strategies and actions in order to maximize  or
or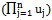 .Definition 1.Complex-Game. We may define a cooperative transformation to be any mapping Ψ, such that if Гis a simple-game in strategic-form, then Ψ(Г) is another complex-game in strategic-form.Entanglement concept and dependence are related. Entanglement is a general physical concept; nevertheless, sometimes it is used in correspondence with mathematical correlation. On the other hand, dependence is a mathematical concept which is more general than correlation because if two stochastic variables ξand ηare uncorrelated (ρ(ξ,η)=0), it does not follow that they are independent, see[16].Definition 2.Dependent Strategy. A dependent (correlated) strategy for N players is any classic probability distribution in (S), where
.Definition 1.Complex-Game. We may define a cooperative transformation to be any mapping Ψ, such that if Гis a simple-game in strategic-form, then Ψ(Г) is another complex-game in strategic-form.Entanglement concept and dependence are related. Entanglement is a general physical concept; nevertheless, sometimes it is used in correspondence with mathematical correlation. On the other hand, dependence is a mathematical concept which is more general than correlation because if two stochastic variables ξand ηare uncorrelated (ρ(ξ,η)=0), it does not follow that they are independent, see[16].Definition 2.Dependent Strategy. A dependent (correlated) strategy for N players is any classic probability distribution in (S), where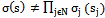 ,
, 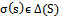 , and
, and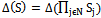 . Note
. Note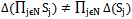 .Theorem 1. If a complex-game (cooperative game) is built such us
.Theorem 1. If a complex-game (cooperative game) is built such us  , or
, or  , then density functions of
, then density functions of  are respectively
are respectively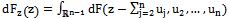 or
or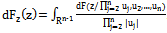 .Proof. Let
.Proof. Let  be random variables with joint distribution function
be random variables with joint distribution function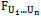 , and
, and  be a Borel function. If we put
be a Borel function. If we put  we see at once that
we see at once that 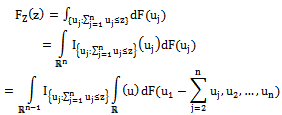 | (1) |
Note that incentive constraint (synergy principle) is respected because in the integral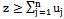 .
.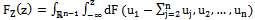 | (2) |
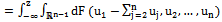 | (3) |
using the last equations we can write the density function of Z.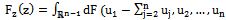 | (4) |
Let  be random variables with joint distribution functions
be random variables with joint distribution functions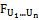 , and
, and 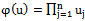 be a Borel function. The synergy principle is taken into account because in the integral
be a Borel function. The synergy principle is taken into account because in the integral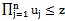 . If we put
. If we put  ; we see at once that:
; we see at once that: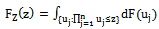 | (5) |
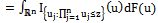 | (6) |
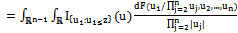 | (7) |
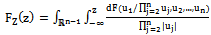 | (8) |
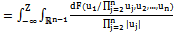 | (9) |
using the last equations we can write the density function of Z.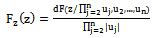 | (10) |
2.1. The Hilbert Space of Random Variables with Finite Second Moment
1. An important role among Banachspaces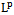 ,
, , is played by the space
, is played by the space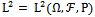 , the space of (equivalence classes of) random variables with finite second moments, see[16], pag 260-280.If ξ and
, the space of (equivalence classes of) random variables with finite second moments, see[16], pag 260-280.If ξ and  , we put the inner product as
, we put the inner product as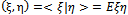 | (11) |
Also, the space 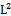 is complete with respect to the norm induced by the scalar product
is complete with respect to the norm induced by the scalar product 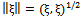 | (12) |
2. Two random variables ξ and 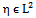 are said to be orthogonal
are said to be orthogonal 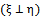 if
if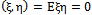 . In other words, they are uncorrelated
. In other words, they are uncorrelated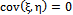 , i.e.
, i.e.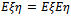 | (13) |
It follows that the properties of being orthogonal and of being uncorrelated coincide for random variables with zero mean values.3. Let 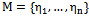 be an orthonormal system and
be an orthonormal system and 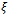 any random variable in
any random variable in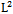 . Consequently the best (in the mean-square sense) estimator forξ in terms of
. Consequently the best (in the mean-square sense) estimator forξ in terms of 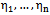 is
is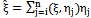 | (14) |
Hilbert space methods are extensively used in probability theory to study properties that depend only on the first two moments of random variables (“ -Theory”).4. Let
-Theory”).4. Let  be Hilbert spaces with bases
be Hilbert spaces with bases 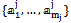 . The tensor product of spaces
. The tensor product of spaces  is denoted by
is denoted by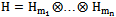 .Using Dirac’s notation, space H has ordered elements
.Using Dirac’s notation, space H has ordered elements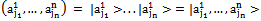 | (15) |
as a basis, thus H has dimension .As in the case of classic and probabilistic systems, the basis states of the compound system H can be thought of
.As in the case of classic and probabilistic systems, the basis states of the compound system H can be thought of  elements. It is natural to represent the general state of the compound system as
elements. It is natural to represent the general state of the compound system as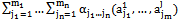 | (16) |
where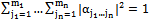 . We say decomposable system if:
. We say decomposable system if: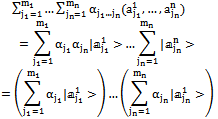 | (17) |
Definition 3. We say that the compound system is entangled if it is not decomposable.
2.2. Correlated Game and ERP Paradox
In Quantum Information Theory, the correlated equilibria in two-player games mean that the associated probabilities of each-player strategies are dependent. Entanglement, according to the Austrian physicist Erwin Shrödinger, which is the essence of Quantum Mechanics, has been known for a long time now to be the source of a number of paradoxical and counterintuitive phenomena. Of those, the most remarkable one is the so-called non-locality, which is at the heart of the Einstein-Podolsky-Rosen paradox (ERP) see[12]pag 12. Einstein, Podolsky and Rosen consider a quantum system consisting of two particles separated by a great distance.“EPR suggests that measurement on particle 1 cannot have any actual influence on particle 2 (locality condition); thus the property of particle 2 must be independent of the measurement performed on particle 1”.Nevertheless, the experiments verified that two particles in the EPR case are always part of one quantum system and thus measurement on one particle changes the possible predictions that can be made for the whole system and therefore for the other particle[5].Moreover, the essence of the EPR argument is as follows. EPR was interested in what termed “elements of reality”. Their belief was that any such element of reality must be represented in any complete physical theory. The goal of the argument was to show that Quantum Mechanics is not a complete physical theory, by identifying elements of reality that were not included in Quantum Mechanics. The way they attempted to do this was by introducing what they claimed was a sufficient condition for a physical property to be an element of reality, namely, that it be possible to predict with certainty the value that property will have, immediately before measurement, see[15].To illustrate, applying “revelation principle” for strategic-form games, the EPR paradox is solved automatically, because this principle demonstrates that all correlated game (entanglement) can be replaced by a communication game, see[14].“...any equilibrium of any communication game can be generated from a strategic-form game Г by adding a system for preplay communication mustbe equivalent to a correlated equilibrium...”Thus, according to[1], “a correlated equilibrium is any correlated strategy for the players in Г that could be self-enforcingly implemented with the help of a mediator who can make nonbinding confidential recommendations to each player.”Finally, nature is optimal and does not need to have replied or equivalent properties simultaneously such as (entanglement /\ communication).Therefore, we are in the presence of an exclusive-or (entanglement \/communication).If in a theoretical or experimental way we can demonstrate that a system (n -player game) is entanglement, then ifis not necessary to speak of communication. In short, game theory helps to resolve EPR paradox.
3. Nash’s Equilibrium in Hilbert Space
The modern description of Quantum Mechanics is profoundly based on linear mappings. Here, we represent the features of linear mappings which are most essential for Quantum Mechanics. Because we mainly concentrate on finite level quantum systems, the vector spaces that are treated hereafter will be assumed to have a finite dimension, unless explicitly stated otherwise, see[7].Let us begin with some terminology: a linear mapping H→H is called an operator. The set of operators on H is denoted L(H): For an operator T; we define the norm of the operator by 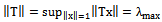 | (18) |
A nonzero vector x∈ H is an eigenvector of T belonging to eigenvalue λ∈ℂ if T x = λ x.Remark 1. With a fixed basis of H; any operator T can be represented as n × n matrix over the field of complex numbers. It is not difficult to see that the matrix representing the adjoint operator T* is the transposed complex conjugate of the matrix representing T.Definition 4. An operator T is selfadjoint if T = T*. An operator T is unitary if T = T-1.Lemma 1. A selfadjoint operator has real eigenvalues. Proof.IfAx = λxthen using braked notation where x = | x > is a column vector and x’ = < x | is a row vector.
of H; any operator T can be represented as n × n matrix over the field of complex numbers. It is not difficult to see that the matrix representing the adjoint operator T* is the transposed complex conjugate of the matrix representing T.Definition 4. An operator T is selfadjoint if T = T*. An operator T is unitary if T = T-1.Lemma 1. A selfadjoint operator has real eigenvalues. Proof.IfAx = λxthen using braked notation where x = | x > is a column vector and x’ = < x | is a row vector.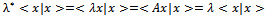 since
since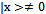 as an eigenvector, it follows that λ* = λ.Lemma 2. The eigenvectors of selfadjoint operators belonging to distinct eigenvalues are orthogonal. Proof. Assume that
as an eigenvector, it follows that λ* = λ.Lemma 2. The eigenvectors of selfadjoint operators belonging to distinct eigenvalues are orthogonal. Proof. Assume that , and
, and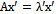 . Since
. Since  are real by the previous lemma,
are real by the previous lemma,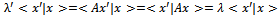 and therefore
and therefore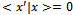 .Theorem 2. The matrix of eigenvectors X is unitary X* = X-1which permits us to write the spectral theorem
.Theorem 2. The matrix of eigenvectors X is unitary X* = X-1which permits us to write the spectral theorem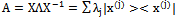 .Proof.Assume that
.Proof.Assume that 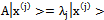 where
where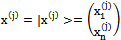 represents a column vector and
represents a column vector and  is a n × n - matrix. Also it is easy to see that
is a n × n - matrix. Also it is easy to see that 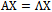 where
where | (19) |
Using matrix properties and vector orthogonality 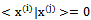 when
when 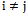 and
and  for all j.
for all j.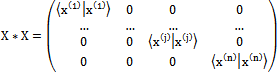 | (20) |
Thus, we conclude that 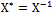 . Here the symbol (*) means hermitian transpose. Finally, using
. Here the symbol (*) means hermitian transpose. Finally, using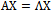 , it is possible to write the spectral theorem.
, it is possible to write the spectral theorem.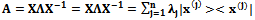 | (21) |
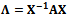 | (22) |
We should revise the following postulates with the purpose of finding a relationship between Nash’s equilibrium and the eigenvalues of Quantum Mechanics operators.First Postulate:At a fixed point t0, the state of a physical system is defined by specifying a ket belonging to the Hilbert space (state space) H.Second Postulate:Every measurable physical quantity A is described by an operator A acting in the state space H.Third Postulate:The only possible result of the measurement of a physical quantity A is one of the eigenvalues of the corresponding observable A. A measurement of A always gives a real value, since A is by definition Hermitian (selfadjoint operator).A measurement process in Quantum Mechanics is the best example of strategic interaction between “human-subject and quantum-object”. Therefore, we have a minimum of two symmetric players when we carry out a measurement process of a physical variable.Theorem 3.The norm of a selfadjoint operator. The maximum eigenvalue
belonging to the Hilbert space (state space) H.Second Postulate:Every measurable physical quantity A is described by an operator A acting in the state space H.Third Postulate:The only possible result of the measurement of a physical quantity A is one of the eigenvalues of the corresponding observable A. A measurement of A always gives a real value, since A is by definition Hermitian (selfadjoint operator).A measurement process in Quantum Mechanics is the best example of strategic interaction between “human-subject and quantum-object”. Therefore, we have a minimum of two symmetric players when we carry out a measurement process of a physical variable.Theorem 3.The norm of a selfadjoint operator. The maximum eigenvalue 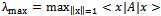 represents the maximum expected value of the selfadjoint operator A and its eigenvector
represents the maximum expected value of the selfadjoint operator A and its eigenvector 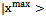 is a fixed point
is a fixed point Proof.The problem to maximize has the next Lagrangian:
Proof.The problem to maximize has the next Lagrangian: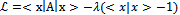 | (23) |
first order condition  implies the equation of eigenvectors.
implies the equation of eigenvectors.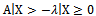 | (24) |
Let max 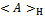 be the maximum expected value in a Hilbert space, using equations (20), (21), (22).
be the maximum expected value in a Hilbert space, using equations (20), (21), (22).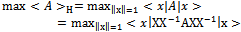 | (25) |
 we can write,
we can write, 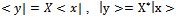 and
and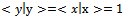 . Using these last equations we have
. Using these last equations we have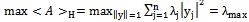 | (26) |
Another form in order to choose 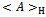 is using the orthogonal eigenvectorxmaxwhere
is using the orthogonal eigenvectorxmaxwhere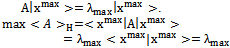 | (27) |
Lemma 3.Nash’s equilibrium in Hilbert space. In mixed strategy Nash’s equilibrium, the eigenvector which maximizes 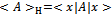 also maximizes expected utility, where
also maximizes expected utility, where and
and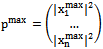 | (28) |
Proof. Let A be the matrix of utilities in a bimatrix game where expected utility is given by 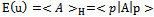 | (29) |
taking into account the properties of the eigenvector matrix X; and of the orthogonal eigenvector 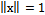 and equations (20), (21), (22).
and equations (20), (21), (22).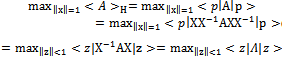 | (30) |
we can write,  , where,
, where, 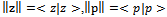 and
and . Using these last equations, we have mixed strategy Nash’s equilibrium.
. Using these last equations, we have mixed strategy Nash’s equilibrium.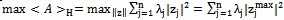 (31)It is evident that there is a vector
(31)It is evident that there is a vector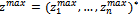 where
where  and
and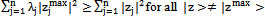 | (32) |
This last result follows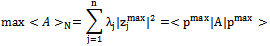 Moreover, in the case of a minimum, the problem can be resolved in a similar way. Finally, obtaining Nash’s equilibrium not only requires fixed point theorem but also maximization of expected utility.Example 1. Let A be a matrix of utilities of a bimatrix symmetrical game.
Moreover, in the case of a minimum, the problem can be resolved in a similar way. Finally, obtaining Nash’s equilibrium not only requires fixed point theorem but also maximization of expected utility.Example 1. Let A be a matrix of utilities of a bimatrix symmetrical game.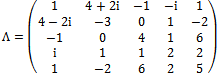 | (32.1) |
Eigenvalues 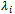 are every one of the diagonal matrix elements of
are every one of the diagonal matrix elements of .
. | (32.2) |
Eigenvectors  permit us to build the matrix
permit us to build the matrix , where
, where 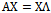 and
and  .
.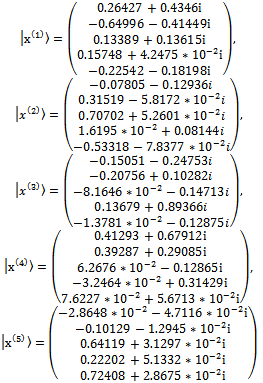 Using equations (25), (26), (27), (30), (31), and (32) by simple inspection, it is possible to verify that
Using equations (25), (26), (27), (30), (31), and (32) by simple inspection, it is possible to verify that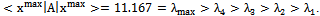 On the other hand, we can see that
On the other hand, we can see that  in the same manner
in the same manner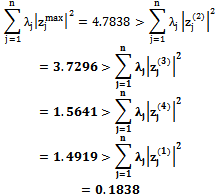 where
where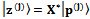 .
.
3.1. Cooperative Games in a Complex System Language
We present cooperative games in the language of Complex Systems. Incentive compatibility is equivalent to synergy principle, which appears naturally (to add or to multiply utilities); on the other hand, coordination and communication have the same implications of correlation, see[14] page 256. Moreover, correlated strategies have a similar concept in Quantum Computing named entanglement. Correlation doesn’t guarantee cooperation although this is equivalent to communication.First, we need to replace the Nash Bargaining solution in two-person symmetric games. We define a bimatrix bargaining problem Г o consist of a pair (F; u) where F is a closed convex subset of ℝ2; u = (u; u) is a vector in ℝ2 and the set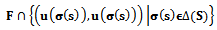 | (33) |
is nonempty and bounded. Here F represents the set of feasible payoff allocations of the feasible set, and v represents the disagreement payoff allocation of the disagreement point. The utility is represented by Second, there is a unique solution Φ(.,.) that satisfies the axioms of Nash´s bargaining solution. This solution function satisfies, for every two-person bargaining problem
Second, there is a unique solution Φ(.,.) that satisfies the axioms of Nash´s bargaining solution. This solution function satisfies, for every two-person bargaining problem ;
;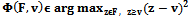 | (34) |
Quantum elements such us photons, electrons, subject-object have symmetrical physical properties and its two- player cooperative solution is the same for each one.Finally, the special case of cooperation between symmetric particles or “human-subject andquantum-object” is when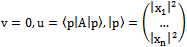 and the Hermitian operator A can have complex or real values aij. Consequently, we can write Φ(F; 0) in Hilbert space
and the Hermitian operator A can have complex or real values aij. Consequently, we can write Φ(F; 0) in Hilbert space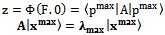 | (35) |
3.1.1. Evolution and Density Operators in Two-Player Symmetric Games
Let us begin to write the expected utility 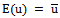 of the operator (symmetric matrix) A that represents utilities. Here, we use Dirac´s notation (braket), where
of the operator (symmetric matrix) A that represents utilities. Here, we use Dirac´s notation (braket), where  represents a column vector or ket and
represents a column vector or ket and  is a row vector or bra, and
is a row vector or bra, and  .
.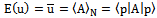 | (36) |
the dynamic replicator equation in matrix form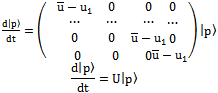 | (37) |
let us write total derivative of expected value 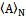
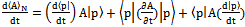 | (38) |
usinga explicit form of 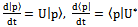 and given that U=U* we can write
and given that U=U* we can write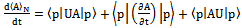 | (39) |
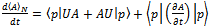 | (40) |
using the nomenclature of an anticonmutator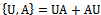
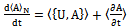 | (41) |
In a similar way, we can find evolution equation of density 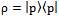
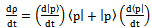 | (42) |
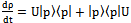 | (43) |
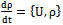 | (44) |
The evolution operator has integrated properties of symmetric games in strategic form and replicator dynamics in matrix form.Steady State. Remember equations (20), (21), (22), specially AX=XΛ and if we suppose that , then it follows that
, then it follows that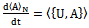 | (45) |
By simple inspection, we can verify that the variable Uof the equation (37) can be written as replacing in equation (45)
replacing in equation (45)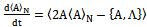 | (46) |
Simplifying equation (46)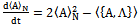 | (47) |
Thus, if steady state is gotten when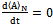 , then
, then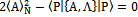 | (48) |
3.2.Tunneling an Explicit Phenomenon of Optimal Cooperation
From viewpoint of classical mechanics, an electron cannot overcome a potential barrier higher than its energy. However, according to quantum mechanics, electrons are not defined by a precise position, but by a cloud of probability. This means that in some systems this probability cloud extends to the other side of a potential barrier. Therefore, the electron can cross the barrier, and for example, to generate electric current. This current is called the tunnel current and it is the control parameter that allows us to describe the topography of any surface.[5],[16].A body with energy less than what is required to overcome or pass through a potential barrier can do it. There is a probability greater than zero, that a body goes through a potential barrier even if less energy is needed.There is a probability greater than zero, to find an object or phenomena associated due to its presence outside the potential barrier of energy higher than the same.Tunnel Effect in Hydrogen BondsConsider us the interaction of two water molecules, which form part of a larger complex, such as salt water clusters, where the NaCl is completely dissociated. If two water molecules form a hydrogen bond, then the hydrogen atom may or may not link to one of the oxygen atoms.[17],[18].In our study we have families of clusters formed as follows: n-Na, n-Cl, n-Na-Cl, n-Cl-Na, n-H2O, with n, m, s element of the natural numbers.n(water molecules)-m(sodium atoms)-s(chlorine atoms). Hydrogen and oxygen atoms of two water molecules are a distance below the threshold. On the other hand, a hydrogen appears uncoupled between two oxygen atoms, that is not linked specifically to any of the two oxygens and your extreme oscillatory motion penetrates the molecular orbitals of the two oxygen atoms, then we have a potential or feasible tunnel effect.When hydrogen atom penetrates the orbital of one of the oxygen atoms, evidently out of the potential barrier of the other oxygen atom and vice versa. This implies that is constantly out of one of the potential barriers or put in another way: there is a probability greater than zero, that an atom leaves a potential barrier having a kinetic energy less than the height of the potential barrier.Theorem.Tunnel effect is a phenomenon that emerges from external incitement such us catalysts presence and when the interior cooperation is maximum.Proof.- Let it be a complex system of n players (quantum objects) i = 1, ..., n, with a total energy E, which is the sum of each of energies Ei. Given a set of thresholds ui, which correspond one to one to each player i, where Ei, which exceeds the respective threshold that player ui .
. .
.
3.2.2. Results
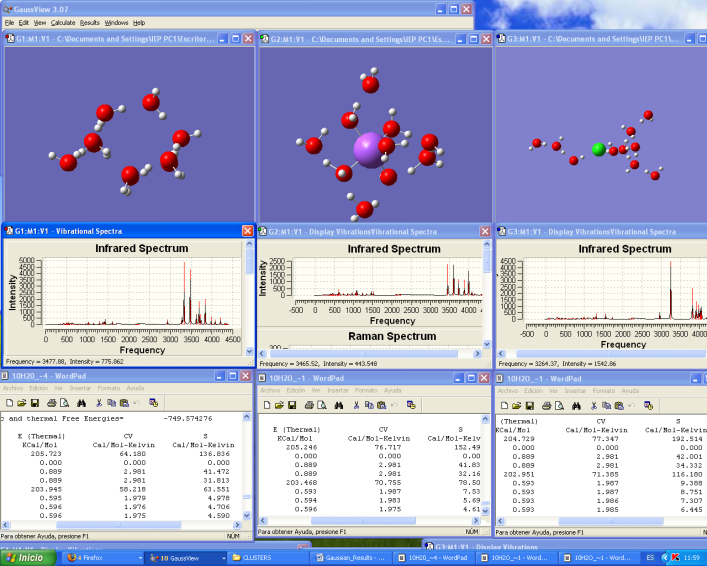
First, according to our interpretation, the second law of thermodynamics is fulfilled, as it explicitly states that "given entropy, system energy is minimal since given energy, system entropy is maximum." We also know that in a state of equilibrium, the values taken by the characteristic parameters of a closed thermodynamic system are such that maximize the value of a certain magnitude called entropy. In this case, we are analyzing two related systems, which change entropy and energy value, this evolution cannot be explained by the second law of thermodynamics but can be explained by Theory of Quantum Games.Second, following Game Theory and the Theory of Quantum Games, we say the optimal evolution of a complex system minimizes the entropy. Figure 1, Figure 2 and Figure 3.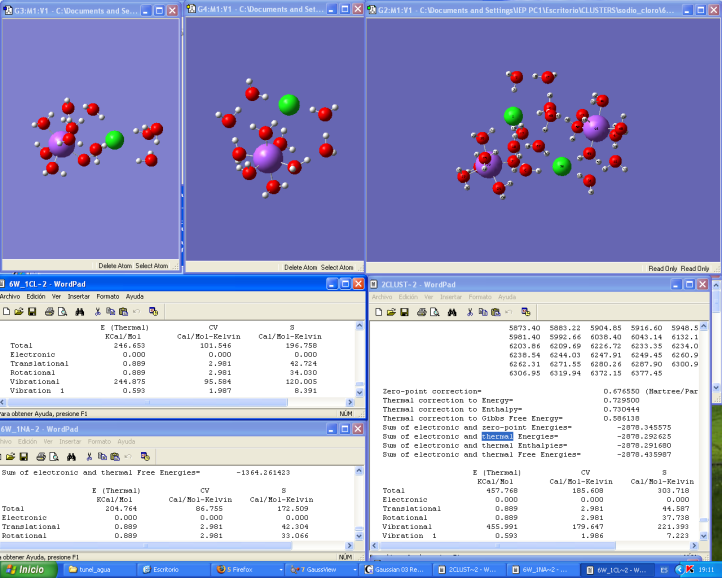 | Figure 1. Cooperation and Minimum Entropy. We can observe, the left side cluster, where there are one sodium atom, one Chloride atom, and twelve water molecules, which are in equilibrium. That is, the balance of forces is zero and the energy of the system is minimal. The intermediate cluster consists of a sodium atom, a Chlorine atom and ten water molecules, also it is in equilibrium. The cluster on the right is the union of the previous clusters. Meanwhile also the right cluster is in equilibrium. The question is what happens to the value of entropy and energy when you bind left cluster on intermediate cluster. Just note that the resulting entropy of joining two clusters is less than the sum of individual entropies. We can verify that 303,718 Cal / Mol-Kelvin < 369.267 Cal / Mol-Kelvin. On the side of the energy we observe to increases: 457.768 Kcal > 451.420 Kcal. Entropy system is decreasing and energy is increasing. What Happens with second law of Thermodynamics with |
Third, on the other hand, the cooperative equilibrium, maximize an objective function called utility, which is exactly equivalent to the energy of a thermodynamic system. In this particular example, we see that in both cases, entropy is minimized but not maximized energy, there is cooperation in the oxygen atoms that are the same type, whereas when there are atoms of different type converge to an equilibrium but not necessarily in a cooperative manner. Figure 2, Figure 3.Fourth, using the analogy in question, we demonstrate experimentally and with the help of Quantum Chemistry that clusters of molecules that interact cooperatively, minimize entropy and maximize energy, which is the fundamental assumption of the Quantum Theory of Cooperative Games, which is the cornerstone of our discussion of tunneling in salt water and its future use. Figure 4.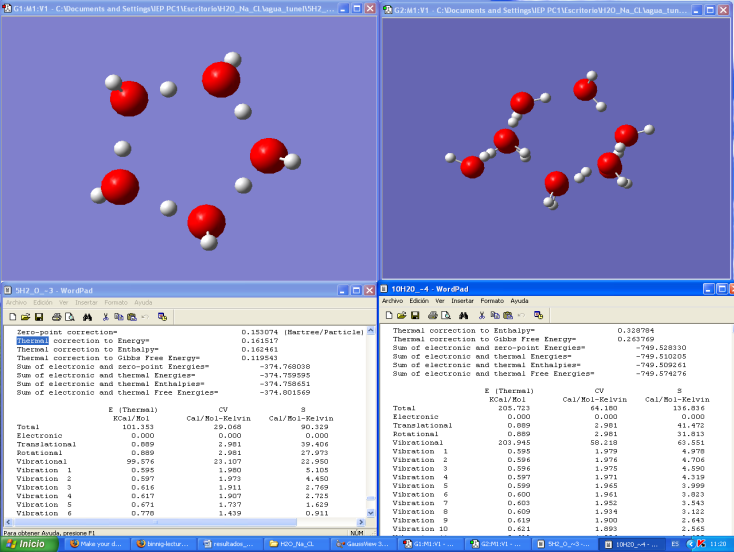 | Figure 2. Left side cluster has 5 H2O molecules and it is in equilibrium. That is, the balance of forces is zero and the energy of the system is minimal. Right side cluster is composed by ten water molecules. Meanwhile also the right cluster is in equilibrium. It is easy to see that entropy resulting from joining two identical clusters is less than the sum of individual entropies. We can verify that 136,836 Cal / Mol-Kelvin < (90.329 + 90.329) Cal / Mol-Kelvin. On the side of energy, we could verify that energy increases: 205.723 Kcal > (101.355 +101,355) kcal. Again, entropy decreases and energy increases, what happens with the second law of thermodynamics |
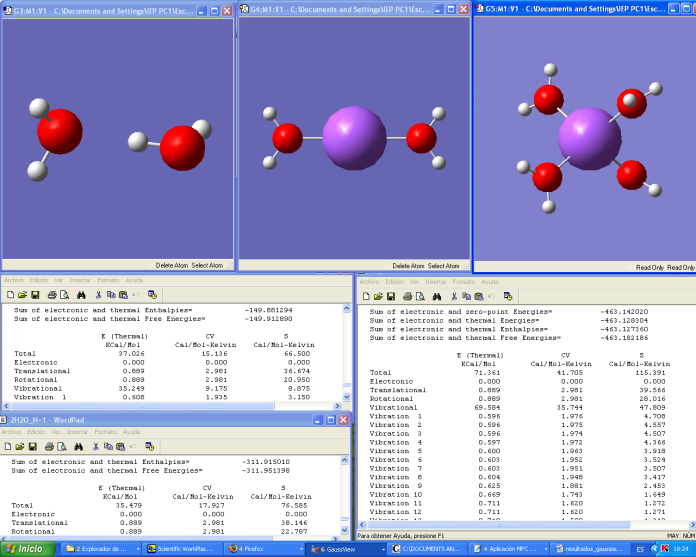 | Figure 3. In left side cluster where there are two water molecules, it is in equilibrium. The intermediate cluster has a sodium atom and two water molecules, also it is optimized. Right side cluster is formed by union of left cluster and intermediate cluster. Meanwhile also right cluster is in equilibrium, according to four Gaussian criteria: Maximum Force, RMS Force, Displacement and RMS Maximum Displacement. It is easy to see that the resulting entropy of merging two clusters, left and middle is less than the sum of individual entropies. We can verify that 115.391 Cal / Mol-Kelvin < (66.585 +76,585) Cal / Mol-Kelvin. On the side of energy, we could verify that energy decreases: 71.361 Kcal< 72.505 Kcal. The entropy and energy decrease. What happens to the second law of thermodynamics |
Fifth, it is evident that pure water clustering tunnel effects not occur due to the non-presence of a NaCl-type catalyst. Figure 2.Finally, theory of cooperative games makes clear that despite obtaining an invariant represented by entropy minimization, it is required energy maximization. Figure 4and Figure 8.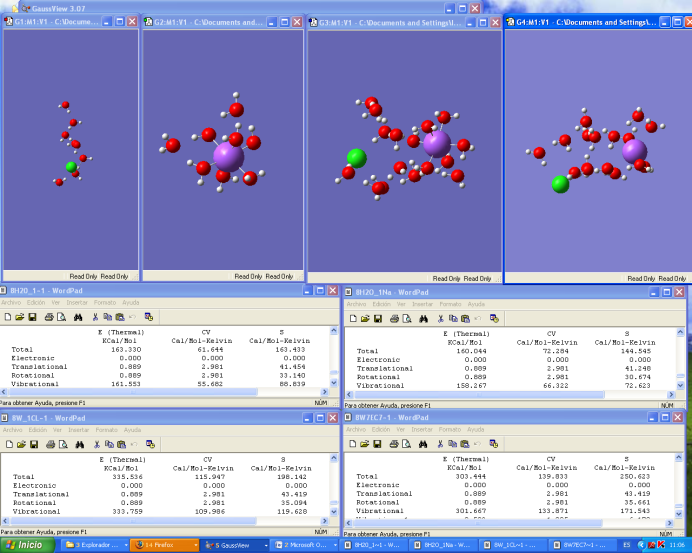 | Figure 4. Cluster three is the union of cluster number one and cluster number three, and each one is in equilibrium. Cluster four is in equilibrium and observing its vibration frequency spectrum, it is clear that they have a large scatter in data, that otherwise have high statistical entropy. Physical entropy value of cluster three is minimal compared to cluster four value (198.42 Cal / Mol-Kelvin < 250.623 Cal / Mol-Kelvin), while its energy is maximum, respectively (335.536 Kcal > 303.44 kcal) |
 | Figure 5. The left spectrum corresponds to third cluster in Figure 4, while the second spectrum corresponds to cluster four. We note in the graph, the spectral line 2825.32 (1/cm) corresponding to a frequency of tunneling, which disappears in the cluster number four |
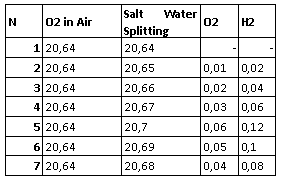 | Figure 6. Using a equipment to measure O2 concentration (AGS-688 y EGA-688 de BRAINBEE), we can verify presence of hydrogen because, when we do photo splitting salt water, appears oxygen and hydrogen simultaneously. In this figure we can see that O2 concentration increase with time, in reference with O2 base concentration equal to 20,64 % and salt concentration 30% wt |
The presence of a positive catalyst lowers the energy of the system, allowing it to develop a reaction with less energy and faster. Increasing effectiveness and reaction output power.Theoretical Results.One player (molecule, quantum element, water) which verifies Nash´s equilibria is intelligent and optimize one utility function. That is the case of salt water.Each physical variable is represented by anHermitian operator whose norm allows us to obtain mixed strategy Nash's equilibrium in Hilbert space.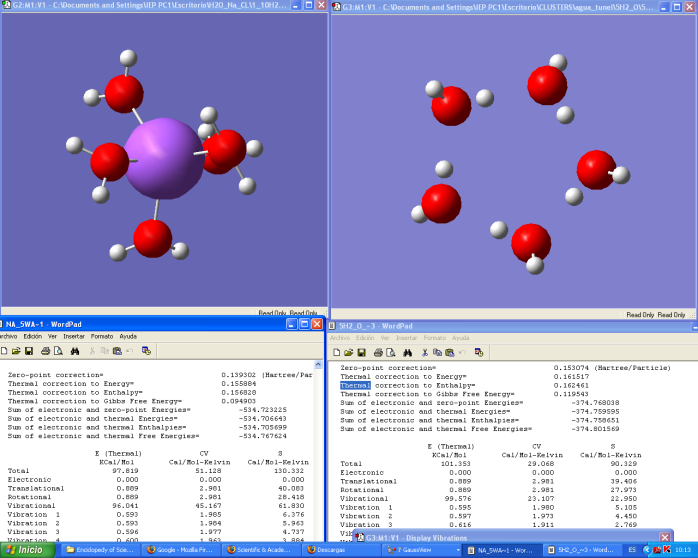 | Figure 7. Differences of energy and entropy in the presence of a catalyst, as the case of sodium. The inner energy of the system without catalyst is lower, while the entropy is higher, which is logical, since the mere presence of the catalyst increases entropy |
 | Figure 8. Variation of internal energy by presence of catalyst. The graphs left, right and middle explain that the internal energy is less when there is no catalyst (left graph). In the case of entropy, we know that it is minimal when there is no catalyst. To sum up, in a system it is verified that the entropy is minimal and the energy is maximum when there is no catalyst |
By virtue of the theorems demonstrated in this paper, properties of Hermitian operators can only be used in symmetric games, which can be represented by complex matrix.Mixed strategy Nash's equilibrium in a bimatrix symmetric game represents a cooperative solution when exist correlation exclusive-or communication.The idea of isolated physical systems has its explanation, the simplification of variables and relationships among the parts. On the contrary, complex systems analyze entirety, synergy and interactions as the cause of a common objective denominated cooperation.The measurement process in Quantum Mechanics and Photocatalysis in Quantum Chemistry is the best example of strategic interaction between "quantum-subject (catalysts) and quantum-object (water) ." Therefore, we have a minimum of two players when we carry out a measurement of a physical variable such us energy, frequency, symmetry, and so on.Lemma named Nash's equilibrium in Hilbert space explains that In mixed strategy Nash's equilibrium, the eigenvector which maximizes  also maximizes expected utility, where: max
also maximizes expected utility, where: max 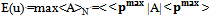 .To use an analogy between utility and energy is explained in Jiménez, E.H (2003a, 2003b).Experimental Results.The presence of a positive catalyst lowers the energy of the system, allowing it to develop a reaction with less energy and faster. Increasing effectiveness and reaction output power. Figure 8.In Figure 4, we can verify that standard deviation of spectrum has a relationship with system entropy.Simple Quantum Catalysis does not verifies Nash´s equilibria (minimum entropy and maximum energy). Figure 8,9.We can see cluster quantum cooperation in figures 1, 2, 4.
.To use an analogy between utility and energy is explained in Jiménez, E.H (2003a, 2003b).Experimental Results.The presence of a positive catalyst lowers the energy of the system, allowing it to develop a reaction with less energy and faster. Increasing effectiveness and reaction output power. Figure 8.In Figure 4, we can verify that standard deviation of spectrum has a relationship with system entropy.Simple Quantum Catalysis does not verifies Nash´s equilibria (minimum entropy and maximum energy). Figure 8,9.We can see cluster quantum cooperation in figures 1, 2, 4.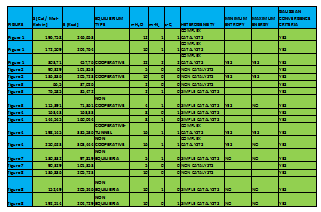 | Figure 9. Equilibria Type as a function of Cooperation |
4. Conclusions
• Each physical variable is represented by anHermitian operator whose norm allows us to obtain mixed strategy Nash’s equilibrium in Hilbert space.• By virtue of the theorems demonstrated in this paper, properties of Hermitian operators can only be used in symmetric games, which can be represented by complex matrix.• Mixed strategy Nash’s equilibrium in a bimatrix symmetric game represents a cooperative solution.• The idea of isolated physical systems has its explanation, the simplification of variables and relationships among the parts. On the contrary, complex systems analyze entirety, synergy and interactions as the cause of a common objective denominated cooperation.• The measurement process in quantum mechanics is the best example of strategic interaction between“human-subject and quantum-object.” Therefore, we have a minimum of two players when we carry out a measurement of a physical variable such us energy, speed, momentum.• In physics, the existence of isolated systems with different unique objectives and disconnected to each other is untenable. This paper shows the necessity of introducing other elements like cooperation and optimality as foundations of the laws of quantum mechanics. We proved that Nash’s equilibrium is the hidden optimal principle of quantum mechanics.• The apparent ERP paradox is completely resolved by using revelation principle for strategic-form games, because it demonstrates that a correlated game is completely equivalent to a communication game.Consequently, it is not necessary to speak of communication and worse even of information speed if a game is already correlated.• Econophysics is both to use rational approaches of economics in the foundations of physics (in special, quantum mechanics) and to transpose physics formalism of quantum theory, statistical mechanics, electrodynamics and others in economics.
References
| [1] | Aumann, R.,“Correlated Equilibria as an Expression of Bayesian Rationality”,Econometrica, 55:1-18, 1987. |
| [2] | Bar-Yam, Y.,“Dynamics of Complex Systems”, Addison-Wesley, Reading, Massachusetts, 1997. |
| [3] | Boccara, N.,“Modeling Complex Systems”, Springer-Verlag, Heidelberg, 2004. |
| [4] | Bouwmeester, D., Eckert, A.,Zeilinger, A.,“The Physics of Quantum Information”, Springer-Verlag, London, UK, 2001. |
| [5] | DrorShafiret all. Resolving the time when an electron exist a tunneling barrier. Nature, Letter. 343-346, 2012. |
| [6] | Einstein, A.,Podolsky, B., Rosen, N., Phys. Rev. 47, 777, 1935. |
| [7] | Hirvensalo, M.,“Quantum Computing”. Springer-Verlag, Berlin, 2001. |
| [8] | Jiménez, E.,“Quantum Games and Minimum Entropy”, Springer, Lecture Notes in Computer Science 2669, Canada, p 216-225, 2003. |
| [9] | Jiménez, E., “Quantum Games: Mixed Strategy Nash’s Equilibrium Represents Minimum Entropy”, Journal of Entropy, Vol 5, Issue4, p 313-347, 2003. |
| [10] | Jiménez, E., Moya, D.,“Econophysics: From Game Theory and Information Theory to Quantum Mechanics”,Physica A, 348C, p 505-543, 2005. |
| [11] | Jiménez, E., “Econophysics Applied to Oil, Banking, Experimental Economics and Business Intelligence”, EPPetroecuador, p 1-340, 2009. |
| [12] | Machiavello, C., Palma, G., Zeilinger, A.,“Quantum Computation and Quantum Information Theory”, World Scientific, London, UK, 2000. |
| [13] | Meyer, P.,“Quantum Probability for Probabilities”, Lecture Notes in Mathematics 1538. Springer-Verlag, Berlin, 1995. |
| [14] | Myerson, R.,“Game Theory Analysis of Conflict”, Massachusetts, 1991. |
| [15] | Morrone J et all. The Journal of Chemical Physics 130. 204511. 2009. |
| [16] | Shiryayev, A.,“Probability”, Springer-Verlag, New York, 1984. |
| [17] | S. Suppiahet all. Clean hydrogen production with the Cu-Cl cycle-Progress of international consortium, I: Experimental unit operations. International Journal of Hydrogen Energy. Vol 36, Iss 24. Pgs 15472-15485. 2012. |
| [18] | Qiang Shao et all. From protein denaturant to protectant: Comparative molecular dynamics study of alcohol/ protein interactions. AIP BioChemical Physics, 2012. |

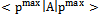 where
where . InHilbert spaces, the norm of a selfadjoint operator (utility matrix: A) permits us to obtain the fixed points
. InHilbert spaces, the norm of a selfadjoint operator (utility matrix: A) permits us to obtain the fixed points , where
, where . A symmetrical matrix is a peculiar case of a selfadjoint operator, which has the advantage of being very usefull in bimatrix symmetrical games. A selfadjoint operator allows us to introduce utilities
. A symmetrical matrix is a peculiar case of a selfadjoint operator, which has the advantage of being very usefull in bimatrix symmetrical games. A selfadjoint operator allows us to introduce utilities 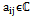 defined on complex numbers.To sum up, Quantum Mechanic axioms are the result of the microscopic cooperative equilibrium among symmetrical players (quantum-object and human-subject). Also, properties of selfadjoint and evolution operators here proved, can be applied to two-player symmetric games. Moreover, this work is an application of econophysics in Quantum Mechanics, see[8],[9].This paper is organized as follows. The first section is a revision of the existent literature about cooperation, entanglement and the Hilbert space of random variables. In the second section, we show the main theorems of complex games and its relationship with entanglement and ERP paradox.In the third section we can see Nash’s equilibrium in Hilbert spaces, evolution operator and steady state. The fourth section is the conclusion of this research.
defined on complex numbers.To sum up, Quantum Mechanic axioms are the result of the microscopic cooperative equilibrium among symmetrical players (quantum-object and human-subject). Also, properties of selfadjoint and evolution operators here proved, can be applied to two-player symmetric games. Moreover, this work is an application of econophysics in Quantum Mechanics, see[8],[9].This paper is organized as follows. The first section is a revision of the existent literature about cooperation, entanglement and the Hilbert space of random variables. In the second section, we show the main theorems of complex games and its relationship with entanglement and ERP paradox.In the third section we can see Nash’s equilibrium in Hilbert spaces, evolution operator and steady state. The fourth section is the conclusion of this research.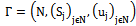 , where N is the set of players,
, where N is the set of players, 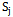 is the set of strategies for player j; and
is the set of strategies for player j; and  is the utility payoff for player j. Here
is the utility payoff for player j. Here  denotes the set of all possible combinations or profiles of strategies that may be chosen by the various players.In general, a randomized strategy is any probability distribution over a set of strategies. We may denote such a randomized strategy in general by
denotes the set of all possible combinations or profiles of strategies that may be chosen by the various players.In general, a randomized strategy is any probability distribution over a set of strategies. We may denote such a randomized strategy in general by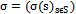 , where
, where 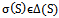 represents the probability of choosing s,
represents the probability of choosing s, 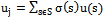 ,
, 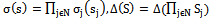 in correlated strategies and
in correlated strategies and  , in non-correlated strategies. Note that in general
, in non-correlated strategies. Note that in general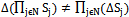 .The concept of cooperation is important in game theory but is somewhat subtle. The term cooperate means "to act together, with a common purpose".The common purpose can be explicit, when players add or multiply energy or utility (synergy principle). Complex game theorem shows us that if we cooperate (to add or to multiply utility), then the results are correlated strategies and actions in order to maximize
.The concept of cooperation is important in game theory but is somewhat subtle. The term cooperate means "to act together, with a common purpose".The common purpose can be explicit, when players add or multiply energy or utility (synergy principle). Complex game theorem shows us that if we cooperate (to add or to multiply utility), then the results are correlated strategies and actions in order to maximize  or
or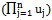 .Definition 1.Complex-Game. We may define a cooperative transformation to be any mapping Ψ, such that if Гis a simple-game in strategic-form, then Ψ(Г) is another complex-game in strategic-form.Entanglement concept and dependence are related. Entanglement is a general physical concept; nevertheless, sometimes it is used in correspondence with mathematical correlation. On the other hand, dependence is a mathematical concept which is more general than correlation because if two stochastic variables ξand ηare uncorrelated (ρ(ξ,η)=0), it does not follow that they are independent, see[16].Definition 2.Dependent Strategy. A dependent (correlated) strategy for N players is any classic probability distribution in (S), where
.Definition 1.Complex-Game. We may define a cooperative transformation to be any mapping Ψ, such that if Гis a simple-game in strategic-form, then Ψ(Г) is another complex-game in strategic-form.Entanglement concept and dependence are related. Entanglement is a general physical concept; nevertheless, sometimes it is used in correspondence with mathematical correlation. On the other hand, dependence is a mathematical concept which is more general than correlation because if two stochastic variables ξand ηare uncorrelated (ρ(ξ,η)=0), it does not follow that they are independent, see[16].Definition 2.Dependent Strategy. A dependent (correlated) strategy for N players is any classic probability distribution in (S), where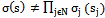 ,
, 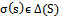 , and
, and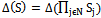 . Note
. Note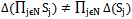 .Theorem 1. If a complex-game (cooperative game) is built such us
.Theorem 1. If a complex-game (cooperative game) is built such us  , or
, or  , then density functions of
, then density functions of  are respectively
are respectively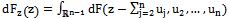 or
or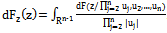 .Proof. Let
.Proof. Let  be random variables with joint distribution function
be random variables with joint distribution function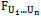 , and
, and  be a Borel function. If we put
be a Borel function. If we put  we see at once that
we see at once that 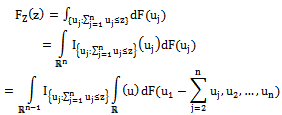
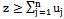 .
.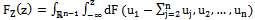
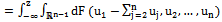
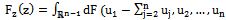
 be random variables with joint distribution functions
be random variables with joint distribution functions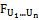 , and
, and 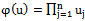 be a Borel function. The synergy principle is taken into account because in the integral
be a Borel function. The synergy principle is taken into account because in the integral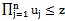 . If we put
. If we put  ; we see at once that:
; we see at once that: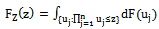
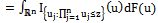
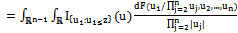
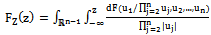
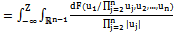
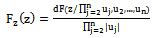
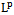 ,
, , is played by the space
, is played by the space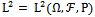 , the space of (equivalence classes of) random variables with finite second moments, see[16], pag 260-280.If ξ and
, the space of (equivalence classes of) random variables with finite second moments, see[16], pag 260-280.If ξ and  , we put the inner product as
, we put the inner product as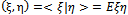
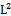 is complete with respect to the norm induced by the scalar product
is complete with respect to the norm induced by the scalar product 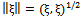
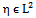 are said to be orthogonal
are said to be orthogonal 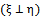 if
if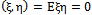 . In other words, they are uncorrelated
. In other words, they are uncorrelated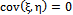 , i.e.
, i.e.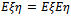
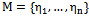 be an orthonormal system and
be an orthonormal system and 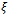 any random variable in
any random variable in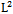 . Consequently the best (in the mean-square sense) estimator forξ in terms of
. Consequently the best (in the mean-square sense) estimator forξ in terms of 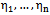 is
is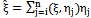
 -Theory”).4. Let
-Theory”).4. Let  be Hilbert spaces with bases
be Hilbert spaces with bases 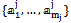 . The tensor product of spaces
. The tensor product of spaces  is denoted by
is denoted by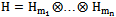 .Using Dirac’s notation, space H has ordered elements
.Using Dirac’s notation, space H has ordered elements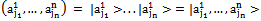
 .As in the case of classic and probabilistic systems, the basis states of the compound system H can be thought of
.As in the case of classic and probabilistic systems, the basis states of the compound system H can be thought of  elements. It is natural to represent the general state of the compound system as
elements. It is natural to represent the general state of the compound system as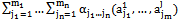
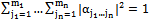 . We say decomposable system if:
. We say decomposable system if: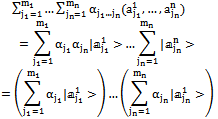
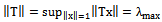
 of H; any operator T can be represented as n × n matrix over the field of complex numbers. It is not difficult to see that the matrix representing the adjoint operator T* is the transposed complex conjugate of the matrix representing T.Definition 4. An operator T is selfadjoint if T = T*. An operator T is unitary if T = T-1.Lemma 1. A selfadjoint operator has real eigenvalues. Proof.IfAx = λxthen using braked notation where x = | x > is a column vector and x’ = < x | is a row vector.
of H; any operator T can be represented as n × n matrix over the field of complex numbers. It is not difficult to see that the matrix representing the adjoint operator T* is the transposed complex conjugate of the matrix representing T.Definition 4. An operator T is selfadjoint if T = T*. An operator T is unitary if T = T-1.Lemma 1. A selfadjoint operator has real eigenvalues. Proof.IfAx = λxthen using braked notation where x = | x > is a column vector and x’ = < x | is a row vector.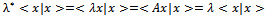 since
since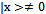 as an eigenvector, it follows that λ* = λ.Lemma 2. The eigenvectors of selfadjoint operators belonging to distinct eigenvalues are orthogonal. Proof. Assume that
as an eigenvector, it follows that λ* = λ.Lemma 2. The eigenvectors of selfadjoint operators belonging to distinct eigenvalues are orthogonal. Proof. Assume that , and
, and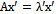 . Since
. Since  are real by the previous lemma,
are real by the previous lemma,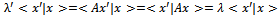 and therefore
and therefore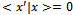 .Theorem 2. The matrix of eigenvectors X is unitary X* = X-1which permits us to write the spectral theorem
.Theorem 2. The matrix of eigenvectors X is unitary X* = X-1which permits us to write the spectral theorem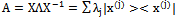 .Proof.Assume that
.Proof.Assume that 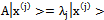 where
where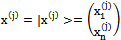 represents a column vector and
represents a column vector and  is a n × n - matrix. Also it is easy to see that
is a n × n - matrix. Also it is easy to see that 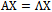 where
where
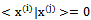 when
when 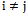 and
and  for all j.
for all j.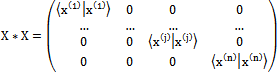
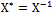 . Here the symbol (*) means hermitian transpose. Finally, using
. Here the symbol (*) means hermitian transpose. Finally, using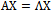 , it is possible to write the spectral theorem.
, it is possible to write the spectral theorem.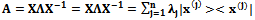
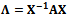
 belonging to the Hilbert space (state space) H.Second Postulate:Every measurable physical quantity A is described by an operator A acting in the state space H.Third Postulate:The only possible result of the measurement of a physical quantity A is one of the eigenvalues of the corresponding observable A. A measurement of A always gives a real value, since A is by definition Hermitian (selfadjoint operator).A measurement process in Quantum Mechanics is the best example of strategic interaction between “human-subject and quantum-object”. Therefore, we have a minimum of two symmetric players when we carry out a measurement process of a physical variable.Theorem 3.The norm of a selfadjoint operator. The maximum eigenvalue
belonging to the Hilbert space (state space) H.Second Postulate:Every measurable physical quantity A is described by an operator A acting in the state space H.Third Postulate:The only possible result of the measurement of a physical quantity A is one of the eigenvalues of the corresponding observable A. A measurement of A always gives a real value, since A is by definition Hermitian (selfadjoint operator).A measurement process in Quantum Mechanics is the best example of strategic interaction between “human-subject and quantum-object”. Therefore, we have a minimum of two symmetric players when we carry out a measurement process of a physical variable.Theorem 3.The norm of a selfadjoint operator. The maximum eigenvalue 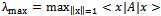 represents the maximum expected value of the selfadjoint operator A and its eigenvector
represents the maximum expected value of the selfadjoint operator A and its eigenvector 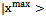 is a fixed point
is a fixed point Proof.The problem to maximize has the next Lagrangian:
Proof.The problem to maximize has the next Lagrangian: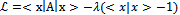
 implies the equation of eigenvectors.
implies the equation of eigenvectors.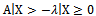
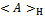 be the maximum expected value in a Hilbert space, using equations (20), (21), (22).
be the maximum expected value in a Hilbert space, using equations (20), (21), (22).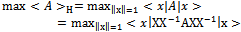
 we can write,
we can write, 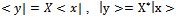 and
and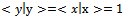 . Using these last equations we have
. Using these last equations we have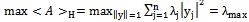
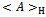 is using the orthogonal eigenvectorxmaxwhere
is using the orthogonal eigenvectorxmaxwhere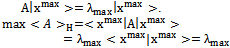
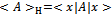 also maximizes expected utility, where
also maximizes expected utility, where and
and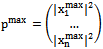
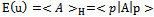
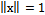 and equations (20), (21), (22).
and equations (20), (21), (22).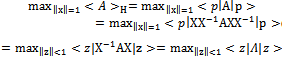
 , where,
, where, 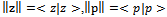 and
and . Using these last equations, we have mixed strategy Nash’s equilibrium.
. Using these last equations, we have mixed strategy Nash’s equilibrium.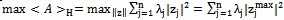 (31)It is evident that there is a vector
(31)It is evident that there is a vector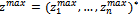 where
where  and
and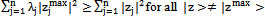
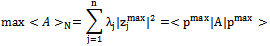 Moreover, in the case of a minimum, the problem can be resolved in a similar way. Finally, obtaining Nash’s equilibrium not only requires fixed point theorem but also maximization of expected utility.Example 1. Let A be a matrix of utilities of a bimatrix symmetrical game.
Moreover, in the case of a minimum, the problem can be resolved in a similar way. Finally, obtaining Nash’s equilibrium not only requires fixed point theorem but also maximization of expected utility.Example 1. Let A be a matrix of utilities of a bimatrix symmetrical game.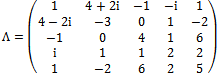
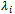 are every one of the diagonal matrix elements of
are every one of the diagonal matrix elements of .
.
 permit us to build the matrix
permit us to build the matrix , where
, where 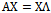 and
and  .
.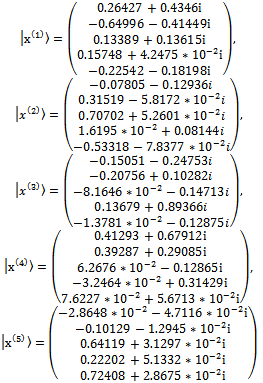 Using equations (25), (26), (27), (30), (31), and (32) by simple inspection, it is possible to verify that
Using equations (25), (26), (27), (30), (31), and (32) by simple inspection, it is possible to verify that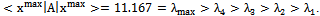 On the other hand, we can see that
On the other hand, we can see that  in the same manner
in the same manner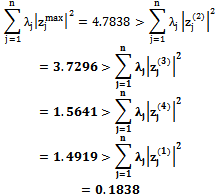 where
where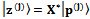 .
.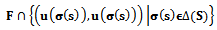
 Second, there is a unique solution Φ(.,.) that satisfies the axioms of Nash´s bargaining solution. This solution function satisfies, for every two-person bargaining problem
Second, there is a unique solution Φ(.,.) that satisfies the axioms of Nash´s bargaining solution. This solution function satisfies, for every two-person bargaining problem ;
;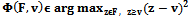
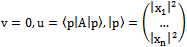 and the Hermitian operator A can have complex or real values aij. Consequently, we can write Φ(F; 0) in Hilbert space
and the Hermitian operator A can have complex or real values aij. Consequently, we can write Φ(F; 0) in Hilbert space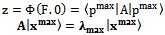
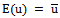 of the operator (symmetric matrix) A that represents utilities. Here, we use Dirac´s notation (braket), where
of the operator (symmetric matrix) A that represents utilities. Here, we use Dirac´s notation (braket), where  represents a column vector or ket and
represents a column vector or ket and  is a row vector or bra, and
is a row vector or bra, and  .
.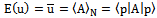
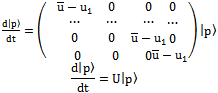
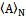
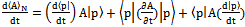
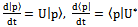 and given that U=U* we can write
and given that U=U* we can write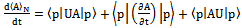
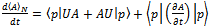
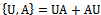
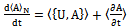
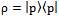
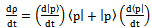
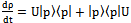
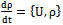
 , then it follows that
, then it follows that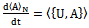
 replacing in equation (45)
replacing in equation (45)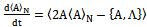
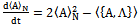
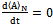 , then
, then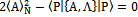
 .
. .
. also maximizes expected utility, where: max
also maximizes expected utility, where: max 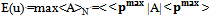 .To use an analogy between utility and energy is explained in Jiménez, E.H (2003a, 2003b).Experimental Results.The presence of a positive catalyst lowers the energy of the system, allowing it to develop a reaction with less energy and faster. Increasing effectiveness and reaction output power. Figure 8.In Figure 4, we can verify that standard deviation of spectrum has a relationship with system entropy.Simple Quantum Catalysis does not verifies Nash´s equilibria (minimum entropy and maximum energy). Figure 8,9.We can see cluster quantum cooperation in figures 1, 2, 4.
.To use an analogy between utility and energy is explained in Jiménez, E.H (2003a, 2003b).Experimental Results.The presence of a positive catalyst lowers the energy of the system, allowing it to develop a reaction with less energy and faster. Increasing effectiveness and reaction output power. Figure 8.In Figure 4, we can verify that standard deviation of spectrum has a relationship with system entropy.Simple Quantum Catalysis does not verifies Nash´s equilibria (minimum entropy and maximum energy). Figure 8,9.We can see cluster quantum cooperation in figures 1, 2, 4.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML






